人教九下数学第28章 锐角三角函数知识点总结及练习(word版无答案)
文档属性
| 名称 | 人教九下数学第28章 锐角三角函数知识点总结及练习(word版无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 194.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-18 00:00:00 | ||
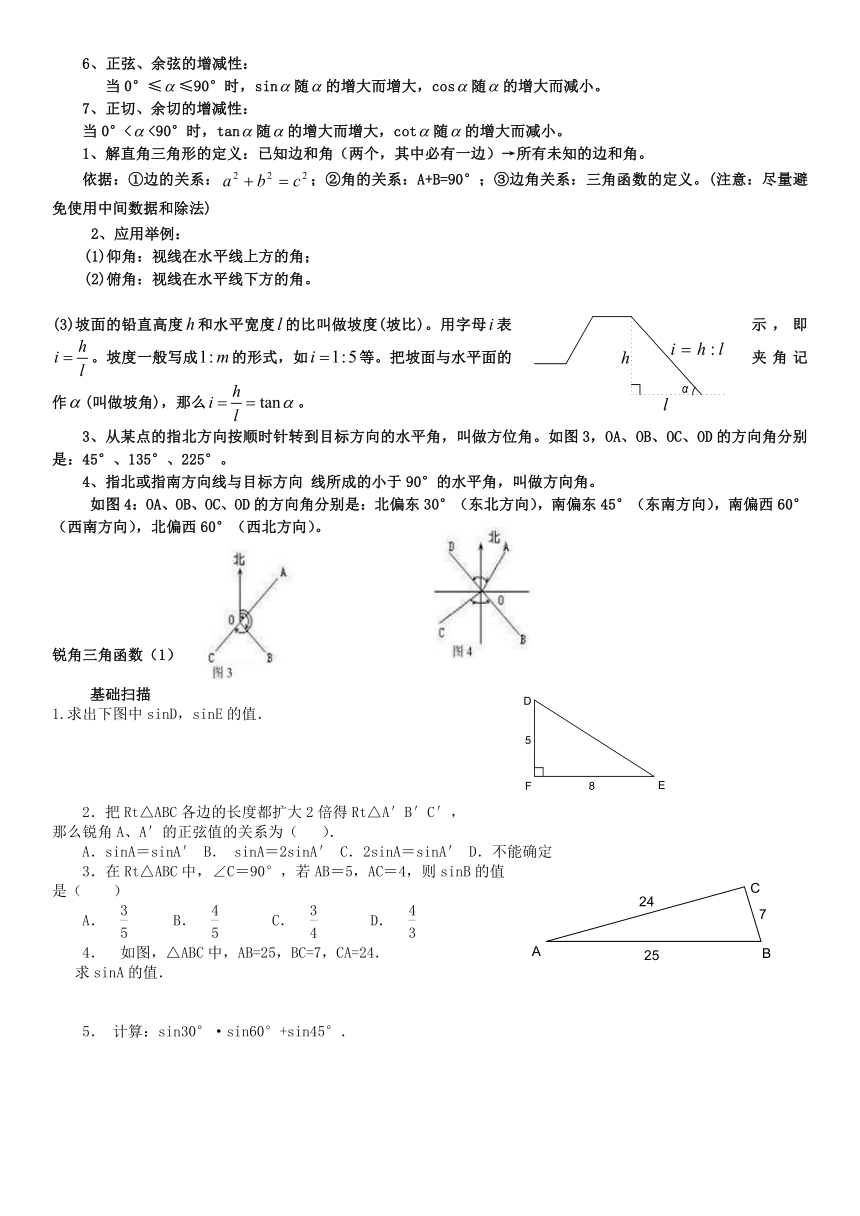
图片预览

文档简介
锐角三角函数知识点总结与习题
1、勾股定理:直角三角形两直角边、的平方和等于斜边的平方。
(
对边
邻边
斜边
A
C
B
)如下图,在Rt△ABC中,∠C为直角,
则∠A的锐角三角函数为(∠A可换成∠B):
定
义
表达式
取值范围
关
系
正弦
(∠A为锐角)
余弦
(∠A为锐角)
正切
(∠A为锐角)
(倒数)
余切
(∠A为锐角)
(
)3、任意锐角的正弦值等于它的余角的余弦值;任意锐角的余弦值等于它的余角的正弦值。
(
)4、任意锐角的正切值等于它的余角的余切值;任意锐角的余切值等于它的余角的正切值。
5、0°、30°、45°、60°、90°特殊角的三角函数值(重要)
三角函数
0°
30°
45°
60°
90°
0
1
1
0
0
1
不存在
不存在
1
0
6、正弦、余弦的增减性:
当0°≤≤90°时,sin随的增大而增大,cos随的增大而减小。
7、正切、余切的增减性:
当0°<<90°时,tan随的增大而增大,cot随的增大而减小。
1、解直角三角形的定义:已知边和角(两个,其中必有一边)→所有未知的边和角。
依据:①边的关系:;②角的关系:A+B=90°;③边角关系:三角函数的定义。(注意:尽量避免使用中间数据和除法)
2、应用举例:
仰角:视线在水平线上方的角;
俯角:视线在水平线下方的角。
(3)坡面的铅直高度和水平宽度的比叫做坡度(坡比)。用字母表示,即。坡度一般写成的形式,如等。把坡面与水平面的夹角记作(叫做坡角),那么。
3、从某点的指北方向按顺时针转到目标方向的水平角,叫做方位角。如图3,OA、OB、OC、OD的方向角分别是:45°、135°、225°。
4、指北或指南方向线与目标方向
线所成的小于90°的水平角,叫做方向角。
如图4:OA、OB、OC、OD的方向角分别是:北偏东30°(东北方向),南偏东45°(东南方向),南偏西60°(西南方向),北偏西60°(西北方向)。
锐角三角函数(1)
基础扫描
1.求出下图中sinD,sinE的值.
把Rt△ABC各边的长度都扩大2倍得Rt△A′B′C′,
那么锐角A、A′的正弦值的关系为(
).
A.sinA=sinA′
B.
sinA=2sinA′
C.2sinA=sinA′
D.不能确定
3.在Rt△ABC中,∠C=90°,若AB=5,AC=4,则sinB的值是(
)
A.
B.
C.
D.
如图,△ABC中,AB=25,BC=7,CA=24.
求sinA的值.
5.
计算:sin30°·sin60°+sin45°.
能力拓展
(
(第6题图)
(第7题图)
)6.
如图,B是线段AC的中点,过点C的直线l与AC成60°的角,在直线上取一点P,连接AP、PB,使sin∠APB=,则满足条件的点P的个数是(
)
A
1个
B
2个
C
3个
D
不存在
8.等腰△ABC中,AB=AC=5,BC=6,求sinA、sinB.
创新学习
如图,△ABC的顶点都是正方形网格中的格点,则sin∠BAC
等于(
)
A.
B.
C.
D.
锐角三角函数(2)
基础扫描
1.
在Rt△ABC中,∠C=90°,a、b、c分别是∠A、∠B、∠C的对边,若b=3a,则tanA=
.
2.
在△ABC中,∠C=90°,cosA=,c=4,则a=_______.
3.
如果是等腰直角三角形的一个锐角,则的值是( )
A.
B.
C.
D.
4.
如图,P是∠α的边OA上一点,且P点坐标为(2,3),
则sinα=_______,cosα=_________,tanα=______
.
5.如图,在△ABC中,∠ACB=90°,CD⊥AB于D,若,,则tan∠ACD的值为(
)
A.
B.
C.
D.
6.
已知α是锐角,且cosα=,求sinα、tanα的值.
能力拓展
7.
若α为锐角,试证明:.
(
(第8题图)
)8.
如图,在Rt△ABC中,CD、CE分别为斜边AB上的高和中线,BC=a,AC=b(b>a),若tan∠DCE=,求的值.
创新学习
9.如图,Rt△ABC中,∠C=90°,D为CA上一点,∠DBC=30°,DA=3,AB=,试求cosA与tanA
的值.
锐角三角函数(3)
基础扫描
1.
已知sinα,则锐角α=
度.
2.
若,则=
.
3.
计算的结果是(
)
A.2
B.
C.1
D..
4.
如图,已知等腰梯形ABCD中,A
B∥CD,∠A=60°,AB=10,CD=3,则此梯形的周长为(
)
A.
25
B.
26
C.
27
D.
28.
5.
计算:
(1)计算:
(2)
先化简,再求值:
+1,其中,
.
(3)已知tanA=2.236,用计算器求锐角A(精确到1度).
能力拓展
6.如图,小明利用一个含60°角的直角三角板测量一栋楼的高度,已知他与楼之间的水平距离BD为10m,眼高AB为1.6m
(即小明的眼睛距地面的距离),那么这栋楼的高是(
)
A.()m
B.21.6m
C.
m
D.m
7.如图,已知AB是半圆O的直径,弦AD、BC相交于点P,若∠DPB=α,那么等于(
)
(
第6题图
第7题图
)
A.sinα
B.COSα
C.tanα
D.
8.如图,⊙O的半径为3,弦AB的长为5.求cosA的值.
创新学习
9.如图,∠C=90°,∠DBC=45°,AB=DB,利用此图求tan22.5°的值.
11、如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的度数为(
)
A.90°
B.60°
C.45°
D.30°
13、
如图,台风中心位于点P,并沿东北方向PQ移动,已知台风移动的速度为30千米/时,受影响区域的半径为200千米,B市位于点P的北偏东75°方向上,距离点P
320千米处.
(1)
说明本次台风会影响B市;
(2)求这次台风影响B市的时间.
1、勾股定理:直角三角形两直角边、的平方和等于斜边的平方。
(
对边
邻边
斜边
A
C
B
)如下图,在Rt△ABC中,∠C为直角,
则∠A的锐角三角函数为(∠A可换成∠B):
定
义
表达式
取值范围
关
系
正弦
(∠A为锐角)
余弦
(∠A为锐角)
正切
(∠A为锐角)
(倒数)
余切
(∠A为锐角)
(
)3、任意锐角的正弦值等于它的余角的余弦值;任意锐角的余弦值等于它的余角的正弦值。
(
)4、任意锐角的正切值等于它的余角的余切值;任意锐角的余切值等于它的余角的正切值。
5、0°、30°、45°、60°、90°特殊角的三角函数值(重要)
三角函数
0°
30°
45°
60°
90°
0
1
1
0
0
1
不存在
不存在
1
0
6、正弦、余弦的增减性:
当0°≤≤90°时,sin随的增大而增大,cos随的增大而减小。
7、正切、余切的增减性:
当0°<<90°时,tan随的增大而增大,cot随的增大而减小。
1、解直角三角形的定义:已知边和角(两个,其中必有一边)→所有未知的边和角。
依据:①边的关系:;②角的关系:A+B=90°;③边角关系:三角函数的定义。(注意:尽量避免使用中间数据和除法)
2、应用举例:
仰角:视线在水平线上方的角;
俯角:视线在水平线下方的角。
(3)坡面的铅直高度和水平宽度的比叫做坡度(坡比)。用字母表示,即。坡度一般写成的形式,如等。把坡面与水平面的夹角记作(叫做坡角),那么。
3、从某点的指北方向按顺时针转到目标方向的水平角,叫做方位角。如图3,OA、OB、OC、OD的方向角分别是:45°、135°、225°。
4、指北或指南方向线与目标方向
线所成的小于90°的水平角,叫做方向角。
如图4:OA、OB、OC、OD的方向角分别是:北偏东30°(东北方向),南偏东45°(东南方向),南偏西60°(西南方向),北偏西60°(西北方向)。
锐角三角函数(1)
基础扫描
1.求出下图中sinD,sinE的值.
把Rt△ABC各边的长度都扩大2倍得Rt△A′B′C′,
那么锐角A、A′的正弦值的关系为(
).
A.sinA=sinA′
B.
sinA=2sinA′
C.2sinA=sinA′
D.不能确定
3.在Rt△ABC中,∠C=90°,若AB=5,AC=4,则sinB的值是(
)
A.
B.
C.
D.
如图,△ABC中,AB=25,BC=7,CA=24.
求sinA的值.
5.
计算:sin30°·sin60°+sin45°.
能力拓展
(
(第6题图)
(第7题图)
)6.
如图,B是线段AC的中点,过点C的直线l与AC成60°的角,在直线上取一点P,连接AP、PB,使sin∠APB=,则满足条件的点P的个数是(
)
A
1个
B
2个
C
3个
D
不存在
8.等腰△ABC中,AB=AC=5,BC=6,求sinA、sinB.
创新学习
如图,△ABC的顶点都是正方形网格中的格点,则sin∠BAC
等于(
)
A.
B.
C.
D.
锐角三角函数(2)
基础扫描
1.
在Rt△ABC中,∠C=90°,a、b、c分别是∠A、∠B、∠C的对边,若b=3a,则tanA=
.
2.
在△ABC中,∠C=90°,cosA=,c=4,则a=_______.
3.
如果是等腰直角三角形的一个锐角,则的值是( )
A.
B.
C.
D.
4.
如图,P是∠α的边OA上一点,且P点坐标为(2,3),
则sinα=_______,cosα=_________,tanα=______
.
5.如图,在△ABC中,∠ACB=90°,CD⊥AB于D,若,,则tan∠ACD的值为(
)
A.
B.
C.
D.
6.
已知α是锐角,且cosα=,求sinα、tanα的值.
能力拓展
7.
若α为锐角,试证明:.
(
(第8题图)
)8.
如图,在Rt△ABC中,CD、CE分别为斜边AB上的高和中线,BC=a,AC=b(b>a),若tan∠DCE=,求的值.
创新学习
9.如图,Rt△ABC中,∠C=90°,D为CA上一点,∠DBC=30°,DA=3,AB=,试求cosA与tanA
的值.
锐角三角函数(3)
基础扫描
1.
已知sinα,则锐角α=
度.
2.
若,则=
.
3.
计算的结果是(
)
A.2
B.
C.1
D..
4.
如图,已知等腰梯形ABCD中,A
B∥CD,∠A=60°,AB=10,CD=3,则此梯形的周长为(
)
A.
25
B.
26
C.
27
D.
28.
5.
计算:
(1)计算:
(2)
先化简,再求值:
+1,其中,
.
(3)已知tanA=2.236,用计算器求锐角A(精确到1度).
能力拓展
6.如图,小明利用一个含60°角的直角三角板测量一栋楼的高度,已知他与楼之间的水平距离BD为10m,眼高AB为1.6m
(即小明的眼睛距地面的距离),那么这栋楼的高是(
)
A.()m
B.21.6m
C.
m
D.m
7.如图,已知AB是半圆O的直径,弦AD、BC相交于点P,若∠DPB=α,那么等于(
)
(
第6题图
第7题图
)
A.sinα
B.COSα
C.tanα
D.
8.如图,⊙O的半径为3,弦AB的长为5.求cosA的值.
创新学习
9.如图,∠C=90°,∠DBC=45°,AB=DB,利用此图求tan22.5°的值.
11、如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的度数为(
)
A.90°
B.60°
C.45°
D.30°
13、
如图,台风中心位于点P,并沿东北方向PQ移动,已知台风移动的速度为30千米/时,受影响区域的半径为200千米,B市位于点P的北偏东75°方向上,距离点P
320千米处.
(1)
说明本次台风会影响B市;
(2)求这次台风影响B市的时间.
