青岛版数学九年级上4.5三角形的内切圆学案
文档属性
| 名称 | 青岛版数学九年级上4.5三角形的内切圆学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 31.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-01 00:00:00 | ||
图片预览

文档简介
4.5三角形的内切圆学案
课前预习案
1.自主学习:学生预习课本130-131
2.知识梳理:
(1、确定圆的条件有哪些?
(2、什么是角平分线?角平分线有哪些性质?
从一个 的顶点引出一条 ,把这个角分成两个相等的角,这条射线叫做这个角的角平分线
(3、右图中△ABC与⊙O有什么关系?
△ABC是⊙O的 三角形;
⊙O是△ABC的 圆
圆心O点叫△ABC的 心,它是 的交点,
它到 的距离相等。
课中探究案
学习目标:
1、通过作图操作,经历三角形内切圆的产生过程;
2、通过作图和探索,体验并理解内心的性质;
3、类比三角形内切圆与三角形外接圆,进一步理解三角形内心和外心所具有的性质;
重难点:三角形内切圆的概念,内心的性质及应用。
学习过程:合作探究(在小组内提出你的问题,合作探究)
(一)、三角形的内切圆
1、李明在一家木料厂上班,工作之余想对厂里的三角形废料进行加工:裁下一块圆形用料,且使圆的面积最大。应该怎样画出裁剪图? 探索:
(1)当裁得圆最大时,圆与三角形的各边有什么位置关系?
(3)做圆的关键是什么?怎样确定圆心,
应该满足什么条件?圆心在什么位置上?
确定圆心之后如何确定圆的半径?
(4).你能作出这个面积最大的圆吗 (尺规作图)
试一试:
归纳小结:
1、和三角形的各边都相切的圆可以作一个且只可以作出一个。
2、三角形内切圆的有关概念(类比联想)
(1)定义:和三角形各边都 的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的 ,这个三角形叫做圆的 三角形。
(2)性质:三角形的内心是三角形的三条 的交点,它到 的距离相等。内心和各顶点相连,则连线 各内角。
(3).三角形的内切圆和三角形的外接圆的类比表:
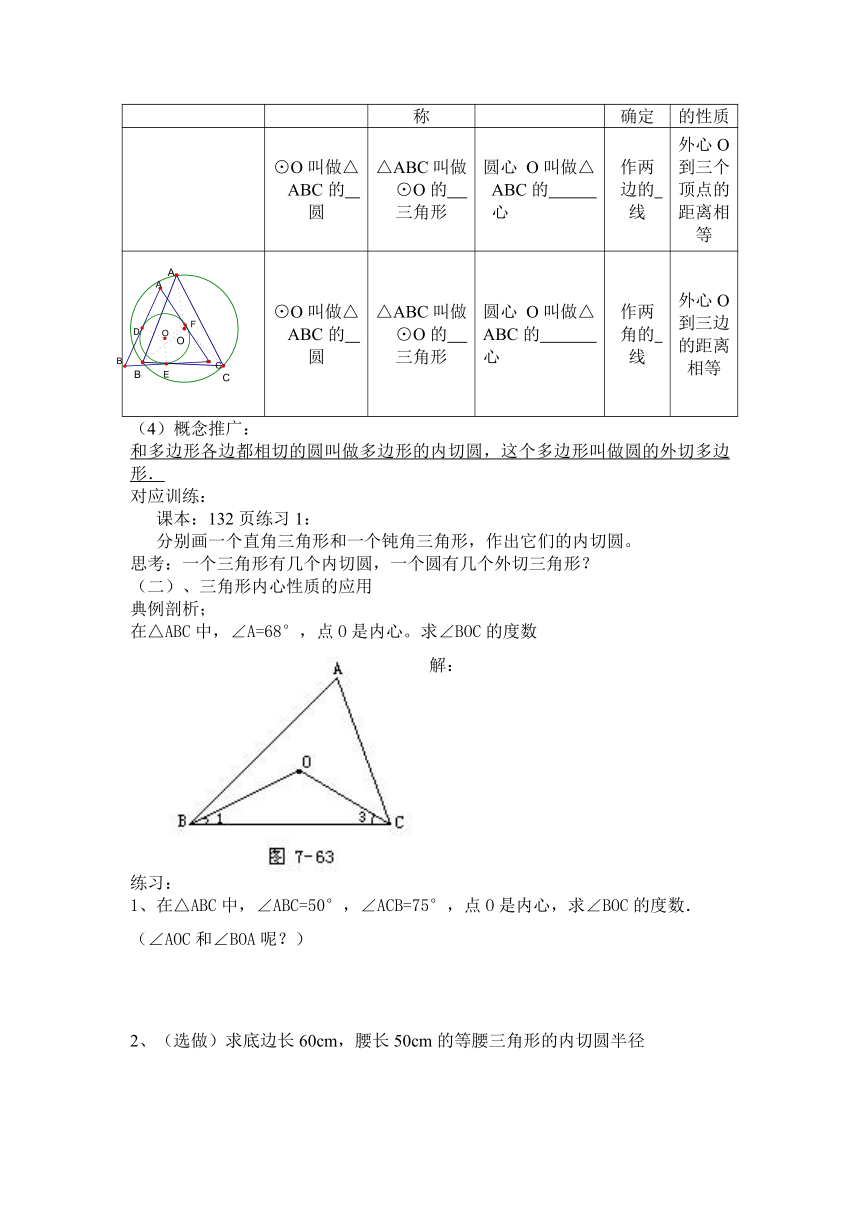
图形 ⊙O的名称 △ABC的名称 圆心O的名称 圆心O确定 “心”的性质
⊙O叫做△ABC的 圆 △ABC叫做⊙O的 三角形 圆心 O叫做△ABC的 心 作两边的 线 外心O到三个顶点的距离相等
⊙O叫做△ABC的 圆 △ABC叫做⊙O的 三角形 圆心 O叫做△ABC的 心 作两角的 线 外心O到三边的距离相等
(4)概念推广:
和多边形各边都相切的圆叫做多边形的内切圆,这个多边形叫做圆的外切多边形.
对应训练:
课本:132页练习1:
分别画一个直角三角形和一个钝角三角形,作出它们的内切圆。
思考:一个三角形有几个内切圆,一个圆有几个外切三角形?
(二)、三角形内心性质的应用
典例剖析;
在△ABC中,∠A=68°,点O是内心。求∠BOC的度数
解:
练习:
在△ABC中,∠ABC=50°,∠ACB=75°,点O是内心,求∠BOC的度数.
(∠AOC和∠BOA呢?)
2、(选做)求底边长60cm,腰长50cm的等腰三角形的内切圆半径
(三)、探究活动:挑战自我
见课本P131 (你能独立完成吗?)
(1)已知的三边长分别为a,b,c.它的内切圆半径为r,你会求的面积吗?
(2)如图1,中,圆I与AB、BC、AC分别相切于D、E、F点。求。(你能运用两种方法解决吗?)
练习:△ABC中,∠C=90°,BC=3,AC=4,求这个三角形的内切圆的半径。
归纳小结:
本节课你学到了什么?说说看。
(四)、达标检测:
1.给出下列命题:①任一个三角形一定有一个外接圆,并且只有一个外接圆;②任一个圆一定有一个内接三角形,并且只有一个内接三角形;③任一个三角形一定有一个内切圆,并且只有一个内切圆;④任一个圆一定有一个外切三角形,并且只有一个外切三角形.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
2.下列图形中,一定有内切圆的四边形是( )
A梯形 B菱形 C矩形 D平行四边形
3. △ABC中,若AB=5,BC=12,AC=13,则它的内切圆半径r=( )
A 2 B 6.5 C 4 D 6
4.如图,⊙O内切于,切点分别为.已知, ,连结,那么等于( )
A. B. C. D.
5.(选做)正三角形内切圆半径r与外接圆半径R之间的关系为( )
A.4R=5r B.3R=4r C.2R=3r D.R=2r
(五)、布置作业,课后延伸:
1.延伸性作业:点I是△ABC的内心,线段AI的延长线交△ ABC的外接圆于点D,交BC边于点E.求证:(1)ID=BD.(2) ID2=DE AD
2、预习性作业:自学课本P133、P134内容。知道两不等圆由远及近有怎样的位置关系?不同的位置关系有什么性质,又是如何判断的?
_
_
_
_
A
_
B
_
C
D O
A
F
C
B
E
课前预习案
1.自主学习:学生预习课本130-131
2.知识梳理:
(1、确定圆的条件有哪些?
(2、什么是角平分线?角平分线有哪些性质?
从一个 的顶点引出一条 ,把这个角分成两个相等的角,这条射线叫做这个角的角平分线
(3、右图中△ABC与⊙O有什么关系?
△ABC是⊙O的 三角形;
⊙O是△ABC的 圆
圆心O点叫△ABC的 心,它是 的交点,
它到 的距离相等。
课中探究案
学习目标:
1、通过作图操作,经历三角形内切圆的产生过程;
2、通过作图和探索,体验并理解内心的性质;
3、类比三角形内切圆与三角形外接圆,进一步理解三角形内心和外心所具有的性质;
重难点:三角形内切圆的概念,内心的性质及应用。
学习过程:合作探究(在小组内提出你的问题,合作探究)
(一)、三角形的内切圆
1、李明在一家木料厂上班,工作之余想对厂里的三角形废料进行加工:裁下一块圆形用料,且使圆的面积最大。应该怎样画出裁剪图? 探索:
(1)当裁得圆最大时,圆与三角形的各边有什么位置关系?
(3)做圆的关键是什么?怎样确定圆心,
应该满足什么条件?圆心在什么位置上?
确定圆心之后如何确定圆的半径?
(4).你能作出这个面积最大的圆吗 (尺规作图)
试一试:
归纳小结:
1、和三角形的各边都相切的圆可以作一个且只可以作出一个。
2、三角形内切圆的有关概念(类比联想)
(1)定义:和三角形各边都 的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的 ,这个三角形叫做圆的 三角形。
(2)性质:三角形的内心是三角形的三条 的交点,它到 的距离相等。内心和各顶点相连,则连线 各内角。
(3).三角形的内切圆和三角形的外接圆的类比表:
图形 ⊙O的名称 △ABC的名称 圆心O的名称 圆心O确定 “心”的性质
⊙O叫做△ABC的 圆 △ABC叫做⊙O的 三角形 圆心 O叫做△ABC的 心 作两边的 线 外心O到三个顶点的距离相等
⊙O叫做△ABC的 圆 △ABC叫做⊙O的 三角形 圆心 O叫做△ABC的 心 作两角的 线 外心O到三边的距离相等
(4)概念推广:
和多边形各边都相切的圆叫做多边形的内切圆,这个多边形叫做圆的外切多边形.
对应训练:
课本:132页练习1:
分别画一个直角三角形和一个钝角三角形,作出它们的内切圆。
思考:一个三角形有几个内切圆,一个圆有几个外切三角形?
(二)、三角形内心性质的应用
典例剖析;
在△ABC中,∠A=68°,点O是内心。求∠BOC的度数
解:
练习:
在△ABC中,∠ABC=50°,∠ACB=75°,点O是内心,求∠BOC的度数.
(∠AOC和∠BOA呢?)
2、(选做)求底边长60cm,腰长50cm的等腰三角形的内切圆半径
(三)、探究活动:挑战自我
见课本P131 (你能独立完成吗?)
(1)已知的三边长分别为a,b,c.它的内切圆半径为r,你会求的面积吗?
(2)如图1,中,圆I与AB、BC、AC分别相切于D、E、F点。求。(你能运用两种方法解决吗?)
练习:△ABC中,∠C=90°,BC=3,AC=4,求这个三角形的内切圆的半径。
归纳小结:
本节课你学到了什么?说说看。
(四)、达标检测:
1.给出下列命题:①任一个三角形一定有一个外接圆,并且只有一个外接圆;②任一个圆一定有一个内接三角形,并且只有一个内接三角形;③任一个三角形一定有一个内切圆,并且只有一个内切圆;④任一个圆一定有一个外切三角形,并且只有一个外切三角形.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
2.下列图形中,一定有内切圆的四边形是( )
A梯形 B菱形 C矩形 D平行四边形
3. △ABC中,若AB=5,BC=12,AC=13,则它的内切圆半径r=( )
A 2 B 6.5 C 4 D 6
4.如图,⊙O内切于,切点分别为.已知, ,连结,那么等于( )
A. B. C. D.
5.(选做)正三角形内切圆半径r与外接圆半径R之间的关系为( )
A.4R=5r B.3R=4r C.2R=3r D.R=2r
(五)、布置作业,课后延伸:
1.延伸性作业:点I是△ABC的内心,线段AI的延长线交△ ABC的外接圆于点D,交BC边于点E.求证:(1)ID=BD.(2) ID2=DE AD
2、预习性作业:自学课本P133、P134内容。知道两不等圆由远及近有怎样的位置关系?不同的位置关系有什么性质,又是如何判断的?
_
_
_
_
A
_
B
_
C
D O
A
F
C
B
E
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
