人教高中数学必修一2.1.2指数函数及其性质(课件)(18张ppt)
文档属性
| 名称 | 人教高中数学必修一2.1.2指数函数及其性质(课件)(18张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 754.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-18 10:51:59 | ||
图片预览





文档简介
(共18张PPT)
指数函数及其性质
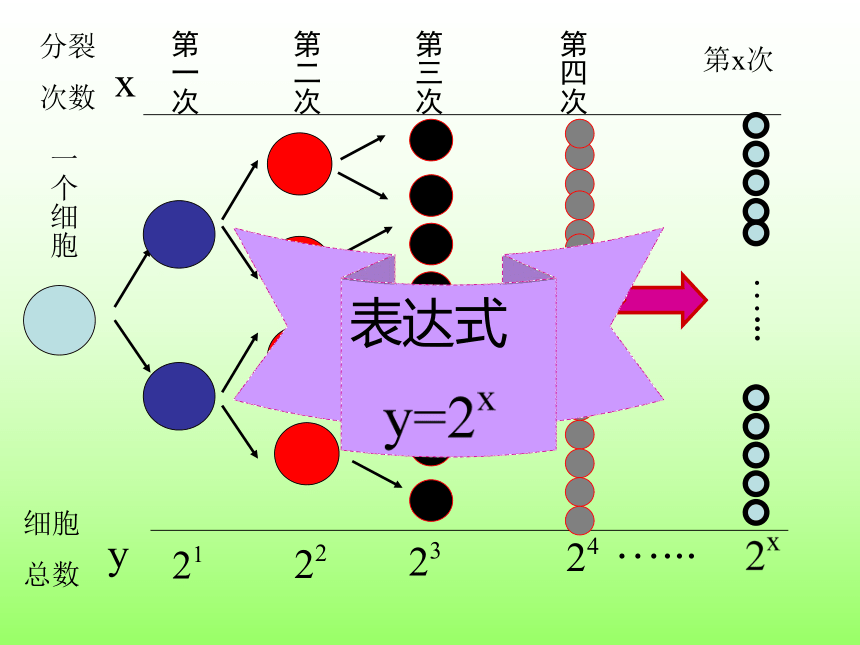
某种细胞分裂时,第一次由1个分裂成2个,第2次由2个分裂成4个,如此下去,如果第x次分裂得到y个细胞,那么细胞个数y与分裂次数x的函数关系是什么?
引例:1
一个细胞
分裂
次数
第一次
第二次
第三次
第四次
第x次
…...
细胞
总数
y
…...
表达式
x
2
一种放射性物质不断衰变为其他物质,每经过一年剩留的质量约是原来的84%.求出这种物质的剩留量随时间(单位:年)变化的函数关系.
设最初的质量为1,时间变量用x表示,剩留量用y表示
则
经过1年,
经过2年,
归纳出:经过x年,
思考:这两个例子的式子有什么共同特征?
底数是常数,指数是变量
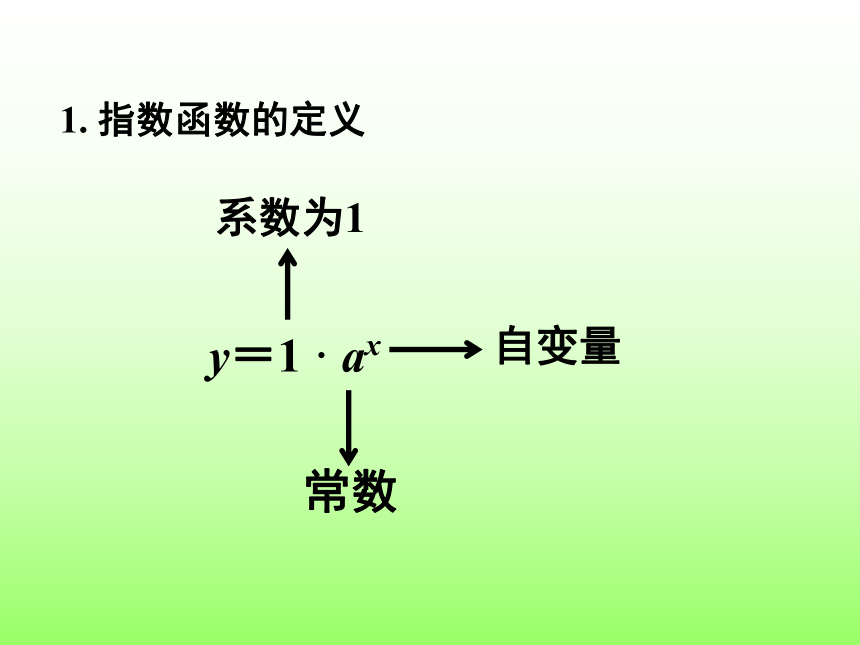
1.
指数函数的定义
常数
自变量
系数为1
y=1
·
ax
定义:一般地,函数
叫做指数函数
注意:
(1)
规定
恒等于零
无意义
无意义
是一个常值函数,无研究必要
(2)形式的严格性:
指数是自变量x,且
整个式子的系数是1
1:指出下列函数那些是指数函数:
答案:(1)(6)(8)是指数函数
2
3:已知y=f(x)是指数函数,且f(2)=4,求函数
y=f(x)的解析式。
画出下列指数函数的图象
…
3
2
1
0
-1
-2
-3
…
x
…
1
3
9
27
…
…
27
9
3
1
…
…
1
2
4
8
…
…
8
4
2
1
…
x
0
1
1
0
1
1
0
1
1
0
1
0
1
0
1
0
1
图
象
性
质
y
x
0
y=1
(0,1)
y=ax
(a>1)
y
x
(0,1)
y=1
0
y=ax
(0定
义
域
:
值
域
:
恒
过
点:
在
R
上是单调
在
R
上是单调
a>1
0R
(
0
,
+
∞
)
(
0
,
1
)
,即
x
=
0
时,
y
=
1
.
增函数
减函数
指数函数
的图像及性质
当
x
>
0
时,y
>
1.
当
x
<
0
时,.
0<
y
<
1
当
x
<
0
时,y
>
1;
当
x
>
0
时,
0<
y
<
1。
例1:
比较下列各题中两值的大小
(1)
1.72.5
与
1.73;
(2)
0.8-01与0.8-02
(3)
与
(4)
与
(5)(0.3)
-0.3
与
(0.2)
-0.3
(6)1.70.3与0.93.1
同底比较大小
不同底但可化同底
不同底但同指数
底不同,指数也不同
同底指数幂比大小,构造指数函数,利用函数单调性
不同底数幂比大小,利用指数函数图像与底的关系比较
利用中间量进行比较
例2:已知下列不等式
,
比较
m,n
的大小
:
(1)
(2)
(3)
课堂练习
1.求下列函数的定义域:
(1)
(2)
(3)函数
恒过点
小结归纳:
通过本节课的学习,你学到了哪些知识?
你又掌握了哪些数学思想方法?
你能将指数函数的学习与实际生活联系起来吗?
习题2-1A组第5、6、7、8题
布置作业:
A先生从今天开始每天给你10万元,而你承担如下任务:第一天给A先生1元,第二天给A先生2元,,第三天给A先生4元,第四天给A先生8元,依次下去…那么,A先生要和你签定15天的合同,你同意吗?又A先生要和你签定30天的合同,你能签这个合同吗?
X
O
Y
X=1
b
a
d
c
思考设a,b,c,d都是不等于1的正数,函数:
在同一直角坐标系中的图象如图所示.
则a,b,c,d的大小关系是
指数函数及其性质
某种细胞分裂时,第一次由1个分裂成2个,第2次由2个分裂成4个,如此下去,如果第x次分裂得到y个细胞,那么细胞个数y与分裂次数x的函数关系是什么?
引例:1
一个细胞
分裂
次数
第一次
第二次
第三次
第四次
第x次
…...
细胞
总数
y
…...
表达式
x
2
一种放射性物质不断衰变为其他物质,每经过一年剩留的质量约是原来的84%.求出这种物质的剩留量随时间(单位:年)变化的函数关系.
设最初的质量为1,时间变量用x表示,剩留量用y表示
则
经过1年,
经过2年,
归纳出:经过x年,
思考:这两个例子的式子有什么共同特征?
底数是常数,指数是变量
1.
指数函数的定义
常数
自变量
系数为1
y=1
·
ax
定义:一般地,函数
叫做指数函数
注意:
(1)
规定
恒等于零
无意义
无意义
是一个常值函数,无研究必要
(2)形式的严格性:
指数是自变量x,且
整个式子的系数是1
1:指出下列函数那些是指数函数:
答案:(1)(6)(8)是指数函数
2
3:已知y=f(x)是指数函数,且f(2)=4,求函数
y=f(x)的解析式。
画出下列指数函数的图象
…
3
2
1
0
-1
-2
-3
…
x
…
1
3
9
27
…
…
27
9
3
1
…
…
1
2
4
8
…
…
8
4
2
1
…
x
0
1
1
0
1
1
0
1
1
0
1
0
1
0
1
0
1
图
象
性
质
y
x
0
y=1
(0,1)
y=ax
(a>1)
y
x
(0,1)
y=1
0
y=ax
(0
义
域
:
值
域
:
恒
过
点:
在
R
上是单调
在
R
上是单调
a>1
0
(
0
,
+
∞
)
(
0
,
1
)
,即
x
=
0
时,
y
=
1
.
增函数
减函数
指数函数
的图像及性质
当
x
>
0
时,y
>
1.
当
x
<
0
时,.
0<
y
<
1
当
x
<
0
时,y
>
1;
当
x
>
0
时,
0<
y
<
1。
例1:
比较下列各题中两值的大小
(1)
1.72.5
与
1.73;
(2)
0.8-01与0.8-02
(3)
与
(4)
与
(5)(0.3)
-0.3
与
(0.2)
-0.3
(6)1.70.3与0.93.1
同底比较大小
不同底但可化同底
不同底但同指数
底不同,指数也不同
同底指数幂比大小,构造指数函数,利用函数单调性
不同底数幂比大小,利用指数函数图像与底的关系比较
利用中间量进行比较
例2:已知下列不等式
,
比较
m,n
的大小
:
(1)
(2)
(3)
课堂练习
1.求下列函数的定义域:
(1)
(2)
(3)函数
恒过点
小结归纳:
通过本节课的学习,你学到了哪些知识?
你又掌握了哪些数学思想方法?
你能将指数函数的学习与实际生活联系起来吗?
习题2-1A组第5、6、7、8题
布置作业:
A先生从今天开始每天给你10万元,而你承担如下任务:第一天给A先生1元,第二天给A先生2元,,第三天给A先生4元,第四天给A先生8元,依次下去…那么,A先生要和你签定15天的合同,你同意吗?又A先生要和你签定30天的合同,你能签这个合同吗?
X
O
Y
X=1
b
a
d
c
思考设a,b,c,d都是不等于1的正数,函数:
在同一直角坐标系中的图象如图所示.
则a,b,c,d的大小关系是
