第十八章 平行四边形 专题训练(含解析)
文档属性
| 名称 | 第十八章 平行四边形 专题训练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 464.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-18 00:00:00 | ||
图片预览


文档简介
人教版八年级下册第十八章平行四边形专题训练
学校:___________姓名:___________班级:___________考号:___________
一、单选题
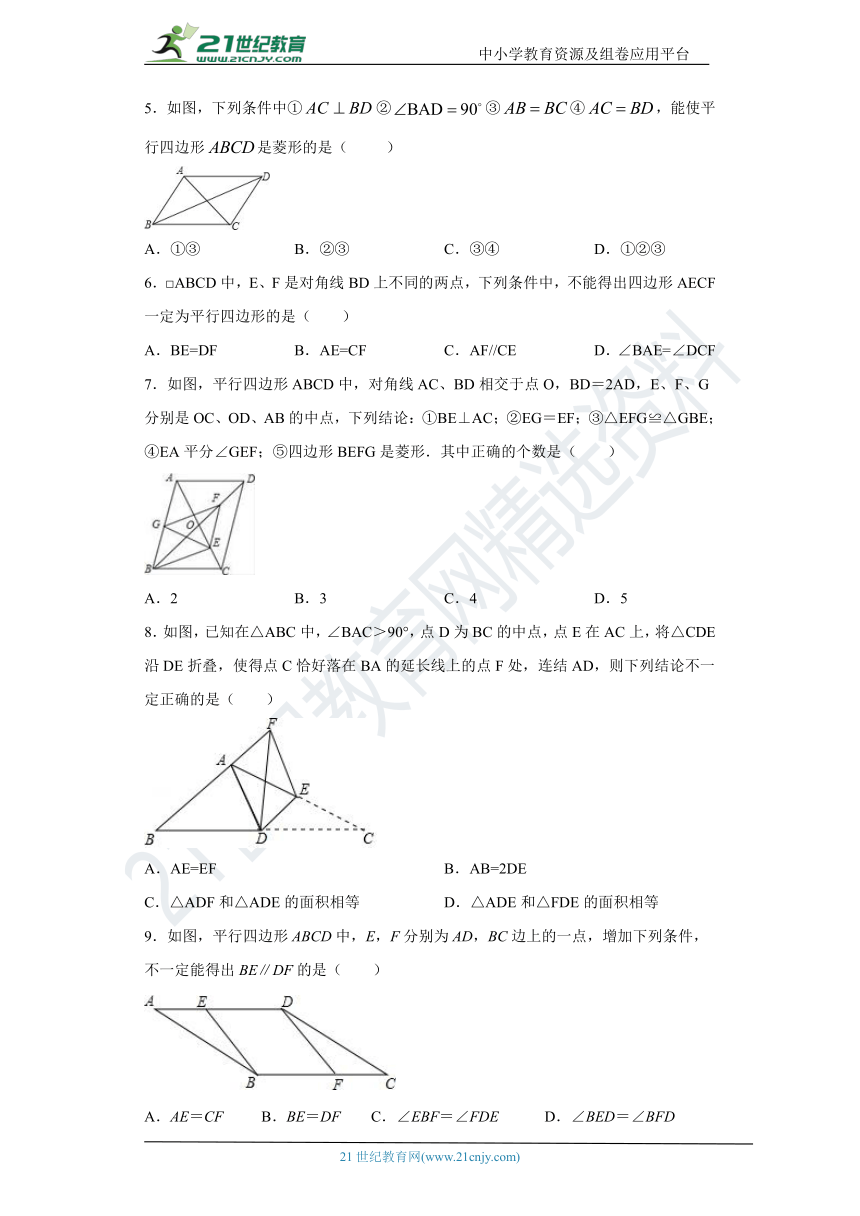
1.如图,已知四边形false是平行四边形,下列结论中不正确的是( )
A.当false时,它是菱形 B.当false时,它是菱形
C.当false时,它是矩形 D.当false时,它是正方形
2.如图,菱形ABCD的对角线AC、BD的长分别为6和8,则这个菱形的周长是( )
A.20 B.24 C.40 D.48
3.如图,将?ABCD沿对角线BD折叠,使点A落在点E处,交BC于点F,若false,false,则false为false false
A.false B.false C.false D.false
4.如图,在正方形false中,false,false分别为false,false的中点,false为对角线false上的一个动点,则下列线段的长等于false最小值的是( )
A.false B.false C.false D.false
5.如图,下列条件中①false②false③false④false,能使平行四边形false是菱形的是( )
A.①③ B.②③ C.③④ D.①②③
6.□ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A.BE=DF B.AE=CF C.AF//CE D.∠BAE=∠DCF
7.如图,平行四边形ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD、AB的中点,下列结论:①BE⊥AC;②EG=EF;③△EFG≌△GBE;④EA平分∠GEF;⑤四边形BEFG是菱形.其中正确的个数是( )
A.2 B.3 C.4 D.5
8.如图,已知在△ABC中,∠BAC>90°,点D为BC的中点,点E在AC上,将△CDE沿DE折叠,使得点C恰好落在BA的延长线上的点F处,连结AD,则下列结论不一定正确的是( )
A.AE=EF B.AB=2DE
C.△ADF和△ADE的面积相等 D.△ADE和△FDE的面积相等
9.如图,平行四边形ABCD中,E,F分别为AD,BC边上的一点,增加下列条件,不一定能得出BE∥DF的是( )
A.AE=CF B.BE=DF C.∠EBF=∠FDE D.∠BED=∠BFD
10.如图,falsefalse的对角线AC,BD相交于点O,false是AB中点,且AE+EO=4,则false的周长为false false
A.20 B.16 C.12 D.8
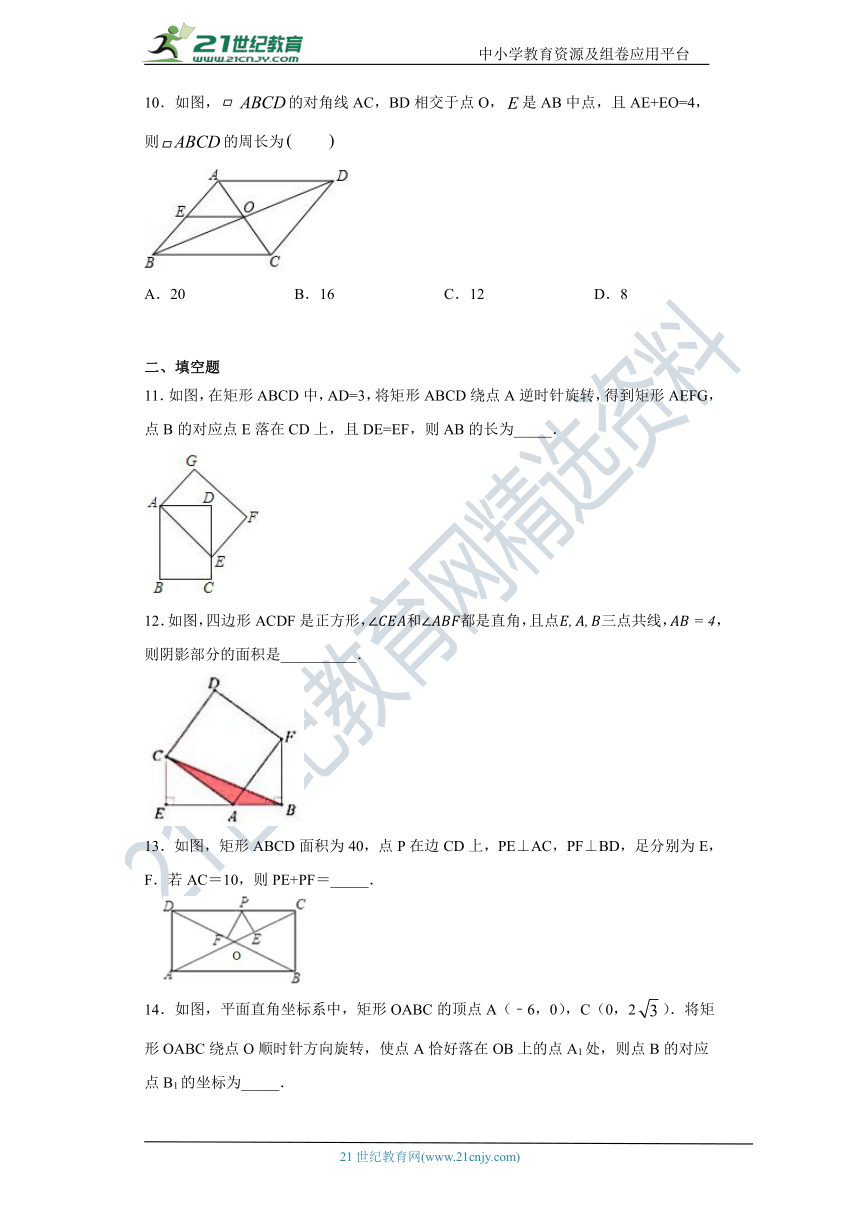
二、填空题
11.如图,在矩形ABCD中,AD=3,将矩形ABCD绕点A逆时针旋转,得到矩形AEFG,点B的对应点E落在CD上,且DE=EF,则AB的长为_____.
12.如图,四边形ACDF是正方形,∠CEA和∠ABF都是直角,且点E,A,B三点共线,AB=4,则阴影部分的面积是__________.
13.如图,矩形ABCD面积为40,点P在边CD上,PE⊥AC,PF⊥BD,足分别为E,F.若AC=10,则PE+PF=_____.
14.如图,平面直角坐标系中,矩形OABC的顶点A(﹣6,0),C(0,2false).将矩形OABC绕点O顺时针方向旋转,使点A恰好落在OB上的点A1处,则点B的对应点B1的坐标为_____.
15.如图,四边形ABCD中,点M,N分别在AB,BC上,∠C=80°,按如图方式沿着MN折叠,使FN∥CD,此时量得∠FMN=40°,则∠B的度数是_____.
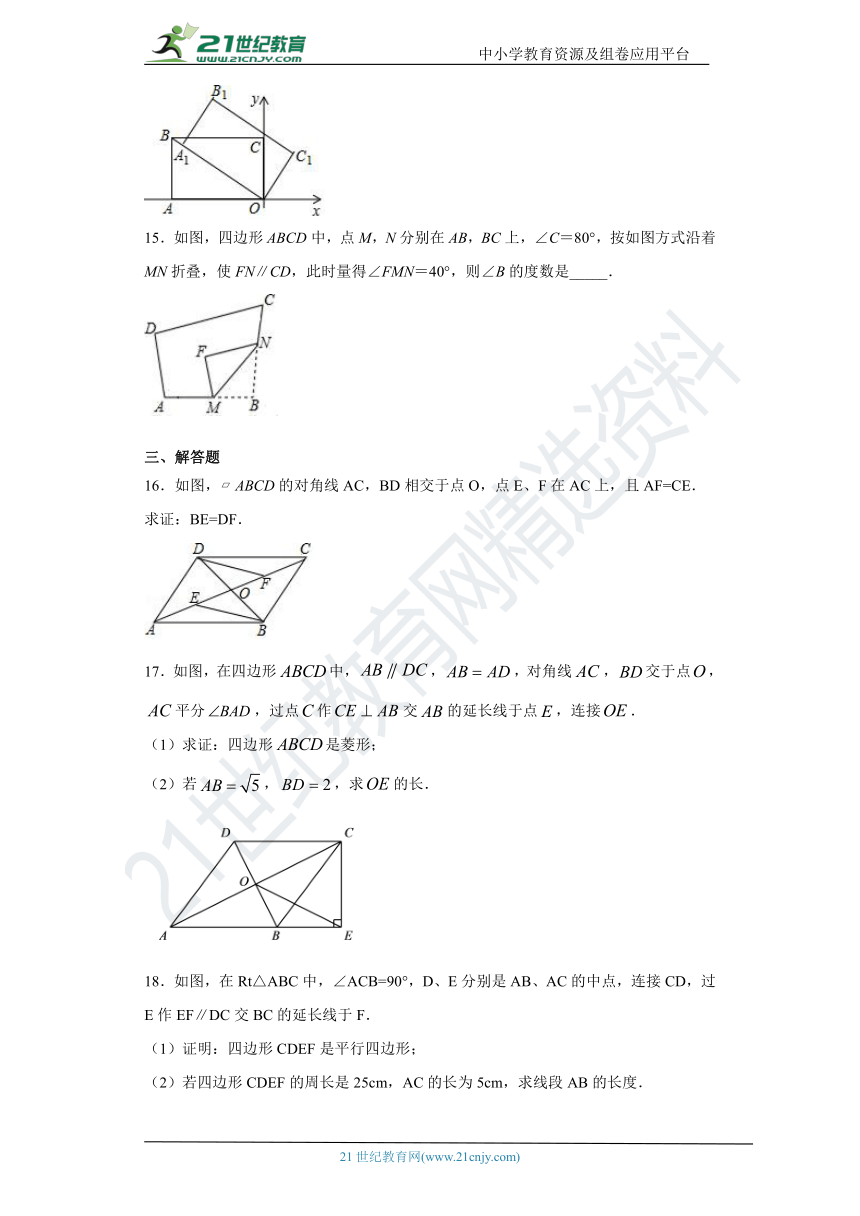
三、解答题
16.如图,?ABCD的对角线AC,BD相交于点O,点E、F在AC上,且AF=CE.
求证:BE=DF.
17.如图,在四边形false中,false,false,对角线false,false交于点false,false平分false,过点false作false交false的延长线于点false,连接false.
(1)求证:四边形false是菱形;
(2)若false,false,求false的长.
18.如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,连接CD,过E作EF∥DC交BC的延长线于F.
(1)证明:四边形CDEF是平行四边形;
(2)若四边形CDEF的周长是25cm,AC的长为5cm,求线段AB的长度.
19.如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.
(1)求证:四边形ACDF是平行四边形;
(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.
参考答案
1.D
解:A、根据邻边相等的平行四边形是菱形可知:四边形ABCD是平行四边形,当AB=BC时,它是菱形,故A选项正确;
B、对角线互相垂直的平行四边形是菱形,∴四边形ABCD是菱形,故B选项正确;
C、有一个角是直角的平行四边形是矩形,故C选项正确;
D、根据对角线相等的平行四边形是矩形可知当AC=BD时,它是矩形,不是菱形,故D选项错误;
综上所述,符合题意是D选项;故选D.
2.A
详解:由菱形对角线性质知,AO=12AC=3,BO=12BD=4,且AO⊥BO,
则AB=AO2+BO2=5,
故这个菱形的周长L=4AB=20.
故选:A.
3.B
解:false,
false,
由折叠可得false,
false,
又false,
false,
又false,
false中,false,
false,
故选B.
4.D
详解:过点E作关于BD的对称点E′,连接AE′,交BD于点P.
∴PA+PE的最小值AE′;
∵E为AD的中点,
∴E′为CD的中点,
∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠ABF=∠AD E′=90°,
∴DE′=BF,
∴ΔABF≌ΔAD E′,
∴AE′=AF.
故选D.
5.A
解:①?ABCD中,AC⊥BD,根据对角线互相垂直的平行四边形是菱形,即可判定?ABCD是菱形;故①正确;
②?ABCD中,∠BAD=90°,根据有一个角是直角的平行四边形是矩形,即可判定?ABCD是矩形,而不能判定?ABCD是菱形;故②错误;
③?ABCD中,AB=BC,根据一组邻边相等的平行四边形是菱形,即可判定?ABCD是菱形;故③正确;
D、?ABCD中,AC=BD,根据对角线相等的平行四边形是矩形,即可判定?ABCD是矩形,而不能判定?ABCD是菱形;故④错误.
故选:A.
6.B
【详解】A、如图,∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,
∵BE=DF,∴OE=OF,∴四边形AECF是平行四边形,故不符合题意;
B、如图所示,AE=CF,不能得到四边形AECF是平行四边形,故符合题意;
C、如图,∵四边形ABCD是平行四边形,∴OA=OC,
∵AF//CE,∴∠FAO=∠ECO,
又∵∠AOF=∠COE,∴△AOF≌△COE,∴AF=CE,
∴AFfalse CE,∴四边形AECF是平行四边形,故不符合题意;
D、如图,∵四边形ABCD是平行四边形,∴AB=CD,AB//CD,
∴∠ABE=∠CDF,
又∵∠BAE=∠DCF,∴△ABE≌△CDF,∴AE=CF,∠AEB=∠CFD,∴∠AEO=∠CFO,
∴AE//CF,
∴AEfalse CF,∴四边形AECF是平行四边形,故不符合题意,
故选B.
7.C
解:∵四边形ABCD是平行四边形,
∴BD=2BO,AD=BC,
∵BD=2AD,
∴BD=2BC,
∴BO=BC,
∵E为OC中点,
∴BE⊥AC,故①成立;
∵BE⊥AC,G是AB中点,
∴EG=falseAB,
∵E、F分别是OC、OD的中点,
∴EF∥CD,且EF=falseCD,
∵四边形ABCD为平行四边形,
∴AB∥CD,且AB=CD,
∴EF=falseAB,
∴EF=EG,故②成立;
∵AB∥CD,EF∥CD,
∴EF∥AB,
∴∠FEG=∠BGE(两直线平行,内错角相等),
在△EFG和△GBE中,
∵BG=FE,∠FEG=∠BGE,GE=EG,
∴△EFG≌△GBE(SAS),即③成立;
∵BG=FE,EF∥AB,
∴四边形BEFG是平行四边形,
∵BE⊥AC,
∴GF⊥AC,
∵EF=EG,
∴∠AEG=∠AEF,
即EA平分∠GEF
故④正确,
若四边形BEFG是菱形
∴BE=BG=falseAB,
∴∠BAC=30°
与题意不符合
故⑤错误
故选C.
8.C
详解:如图,连接CF,
∵点D是BC中点,
∴BD=CD,
由折叠知,∠ACB=∠DFE,CD=DF,
∴BD=CD=DF,
∴△BFC是直角三角形,
∴∠BFC=90°,
∵BD=DF,
∴∠B=∠BFD,
∴∠EAF=∠B+∠ACB=∠BFD+∠DFE=∠AFE,
∴AE=EF,故A正确,
由折叠知,EF=CE,
∴AE=CE,
∵BD=CD,
∴DE是△ABC的中位线,
∴AB=2DE,故B正确,
∵AE=CE,
∴S△ADE=S△CDE,
由折叠知,△CDE≌△△FDE,
∴S△CDE=S△FDE,
∴S△ADE=S△FDE,故D正确,
∴C选项不正确,
故选:C.
9.B
解:false四边形ABCD是平行四边形,
∴AD//BC,AD=BC,
A、∵AE=CF,
∴DE=BF,
∴四边形BFDE是平行四边形,
∴BE//DF,故本选项能判定BE//DF;
B、∵BE=DF,
false四边形BFDE是等腰梯形,
false本选项不一定能判定BE//DF;
C、∵AD//BC,
∴∠BED+∠EBF=180°,∠EDF+∠BFD=180°,
∵∠EBF=∠FDE,
∴∠BED=∠BFD,
false四边形BFDE是平行四边形,
∴BE//DF,
故本选项能判定BE//DF;
D、∵AD//BC,
∴∠BED+∠EBF=180°,∠EDF+∠BFD=180°,
∵∠BED=∠BFD,
∴∠EBF=∠FDE,
∴四边形BFDE是平行四边形,
∴BE//DF,故本选项能判定BE//DF.
故选:B.
10.B
解:∵四边形ABCD是平行四边形,
∴OA=OC,
∵AE=EB,
∴OE=falseBC,
∵AE+EO=4,
∴2AE+2EO=8,
∴AB+BC=8,
∴平行四边形ABCD的周长=2×8=16,
故选:B.
11.3false
【详解】∵四边形ABCD是矩形,∴∠D=90°,BC=AD=3,
∵将矩形ABCD绕点A逆时针旋转得到矩形AEFG,
∴EF=BC=3,AE=AB,
∵DE=EF,
∴AD=DE=3,
∴AE=false=3false,
∴AB=3false,
故答案为:3false.
12.8
【详解】∵四边形ACDF是正方形,
∴AC=FA,∠CAF=90°,
∴∠CAE+∠FAB=90°,
∵∠CEA=90°,∴∠CAE+∠ACE=90°,
∴∠ACE=∠FAB,
又∵∠AEC=∠FBA=90°,
∴△AEC≌△FBA,
∴CE=AB=4,
∴S阴影=12AB·CE=8,
故答案为:8.
13.4
解:如图,设AC与BD的交点为O,连接PO,
∵四边形ABCD是矩形
∴AO=CO=5=BO=DO,
∴S△DCO=falseS矩形ABCD=10,
∵S△DCO=S△DPO+S△PCO,
∴10=false×DO×PF+false×OC×PE
∴20=5PF+5PE
∴PE+PF=4
故答案为:4
14.(-2false,6)
详解:连接OB1,作B1H⊥OA于H,
由题意得,OA=6,AB=OC-2false,
则tan∠BOA=false,
∴∠BOA=30°,
∴∠OBA=60°,
由旋转的性质可知,∠B1OB=∠BOA=30°,
∴∠B1OH=60°,
在△AOB和△HB1O,
false,
∴△AOB≌△HB1O,
∴B1H=OA=6,OH=AB=2false,
∴点B1的坐标为(-2false,6),
故答案为:(-2false,6).
15.100°
解:∵FN∥DC,
∴∠BNF=∠C=80°,
∵△BMN沿MN翻折得△FMN,
∴∠BMN=∠FMN=40°,
∠BNM=false∠BNF=false×80°=40°,
在△BMN中,∠B=180°﹣(∠BMN+∠BNM)=180°﹣(40°+40°)=180°﹣80°=100°.
故答案为:100°.
16.证明见解析.
详解:∵四边形ABCD是平行四边形,
∴OA=OC,OD=OB,
∵AE=CF,
∴OE=OF,
在△BEO和△DFO中,false,
∴△BEO≌△DFO,
∴BE=DF.
17.(1)证明见解析;(2)2.
详解:(1)证明:∵false∥false,
∴false
∵false平分false
∴false,
∴false
∴false
又∵false
∴false
又∵false∥false,
∴四边形false是平行四边形
又∵false
∴false是菱形
(2)解:∵四边形false是菱形,对角线false、false交于点false.
∴false.false,false,
∴false.
在false中,false.
∴false.
∵false,
∴false.
在false中,false.false为false中点.
∴false.
18.(1)证明见解析;(2)AB=13cm,
【详解】(1)∵D、E分别是AB、AC的中点,F是BC延长线上的一点,
∴ED是Rt△ABC的中位线,
∴ED∥FC.BC=2DE,
又 EF∥DC,
∴四边形CDEF是平行四边形;
(2)∵四边形CDEF是平行四边形;
∴DC=EF,
∵DC是Rt△ABC斜边AB上的中线,
∴AB=2DC,
∴四边形DCFE的周长=AB+BC,
∵四边形DCFE的周长为25cm,AC的长5cm,
∴BC=25﹣AB,
∵在Rt△ABC中,∠ACB=90°,
∴AB2=BC2+AC2,即AB2=(25﹣AB)2+52,
解得,AB=13cm.
19.(1)证明见解析;(2)BC=2CD,理由见解析.
详解:(1)∵四边形ABCD是矩形,
∴AB∥CD,
∴∠FAE=∠CDE,
∵E是AD的中点,
∴AE=DE,
又∵∠FEA=∠CED,
∴△FAE≌△CDE,
∴CD=FA,
又∵CD∥AF,
∴四边形ACDF是平行四边形;
(2)BC=2CD.
证明:∵CF平分∠BCD,
∴∠DCE=45°,
∵∠CDE=90°,
∴△CDE是等腰直角三角形,
∴CD=DE,
∵E是AD的中点,
∴AD=2CD,
∵AD=BC,
∴BC=2CD.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,已知四边形false是平行四边形,下列结论中不正确的是( )
A.当false时,它是菱形 B.当false时,它是菱形
C.当false时,它是矩形 D.当false时,它是正方形
2.如图,菱形ABCD的对角线AC、BD的长分别为6和8,则这个菱形的周长是( )
A.20 B.24 C.40 D.48
3.如图,将?ABCD沿对角线BD折叠,使点A落在点E处,交BC于点F,若false,false,则false为false false
A.false B.false C.false D.false
4.如图,在正方形false中,false,false分别为false,false的中点,false为对角线false上的一个动点,则下列线段的长等于false最小值的是( )
A.false B.false C.false D.false
5.如图,下列条件中①false②false③false④false,能使平行四边形false是菱形的是( )
A.①③ B.②③ C.③④ D.①②③
6.□ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A.BE=DF B.AE=CF C.AF//CE D.∠BAE=∠DCF
7.如图,平行四边形ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD、AB的中点,下列结论:①BE⊥AC;②EG=EF;③△EFG≌△GBE;④EA平分∠GEF;⑤四边形BEFG是菱形.其中正确的个数是( )
A.2 B.3 C.4 D.5
8.如图,已知在△ABC中,∠BAC>90°,点D为BC的中点,点E在AC上,将△CDE沿DE折叠,使得点C恰好落在BA的延长线上的点F处,连结AD,则下列结论不一定正确的是( )
A.AE=EF B.AB=2DE
C.△ADF和△ADE的面积相等 D.△ADE和△FDE的面积相等
9.如图,平行四边形ABCD中,E,F分别为AD,BC边上的一点,增加下列条件,不一定能得出BE∥DF的是( )
A.AE=CF B.BE=DF C.∠EBF=∠FDE D.∠BED=∠BFD
10.如图,falsefalse的对角线AC,BD相交于点O,false是AB中点,且AE+EO=4,则false的周长为false false
A.20 B.16 C.12 D.8
二、填空题
11.如图,在矩形ABCD中,AD=3,将矩形ABCD绕点A逆时针旋转,得到矩形AEFG,点B的对应点E落在CD上,且DE=EF,则AB的长为_____.
12.如图,四边形ACDF是正方形,∠CEA和∠ABF都是直角,且点E,A,B三点共线,AB=4,则阴影部分的面积是__________.
13.如图,矩形ABCD面积为40,点P在边CD上,PE⊥AC,PF⊥BD,足分别为E,F.若AC=10,则PE+PF=_____.
14.如图,平面直角坐标系中,矩形OABC的顶点A(﹣6,0),C(0,2false).将矩形OABC绕点O顺时针方向旋转,使点A恰好落在OB上的点A1处,则点B的对应点B1的坐标为_____.
15.如图,四边形ABCD中,点M,N分别在AB,BC上,∠C=80°,按如图方式沿着MN折叠,使FN∥CD,此时量得∠FMN=40°,则∠B的度数是_____.
三、解答题
16.如图,?ABCD的对角线AC,BD相交于点O,点E、F在AC上,且AF=CE.
求证:BE=DF.
17.如图,在四边形false中,false,false,对角线false,false交于点false,false平分false,过点false作false交false的延长线于点false,连接false.
(1)求证:四边形false是菱形;
(2)若false,false,求false的长.
18.如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,连接CD,过E作EF∥DC交BC的延长线于F.
(1)证明:四边形CDEF是平行四边形;
(2)若四边形CDEF的周长是25cm,AC的长为5cm,求线段AB的长度.
19.如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.
(1)求证:四边形ACDF是平行四边形;
(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.
参考答案
1.D
解:A、根据邻边相等的平行四边形是菱形可知:四边形ABCD是平行四边形,当AB=BC时,它是菱形,故A选项正确;
B、对角线互相垂直的平行四边形是菱形,∴四边形ABCD是菱形,故B选项正确;
C、有一个角是直角的平行四边形是矩形,故C选项正确;
D、根据对角线相等的平行四边形是矩形可知当AC=BD时,它是矩形,不是菱形,故D选项错误;
综上所述,符合题意是D选项;故选D.
2.A
详解:由菱形对角线性质知,AO=12AC=3,BO=12BD=4,且AO⊥BO,
则AB=AO2+BO2=5,
故这个菱形的周长L=4AB=20.
故选:A.
3.B
解:false,
false,
由折叠可得false,
false,
又false,
false,
又false,
false中,false,
false,
故选B.
4.D
详解:过点E作关于BD的对称点E′,连接AE′,交BD于点P.
∴PA+PE的最小值AE′;
∵E为AD的中点,
∴E′为CD的中点,
∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠ABF=∠AD E′=90°,
∴DE′=BF,
∴ΔABF≌ΔAD E′,
∴AE′=AF.
故选D.
5.A
解:①?ABCD中,AC⊥BD,根据对角线互相垂直的平行四边形是菱形,即可判定?ABCD是菱形;故①正确;
②?ABCD中,∠BAD=90°,根据有一个角是直角的平行四边形是矩形,即可判定?ABCD是矩形,而不能判定?ABCD是菱形;故②错误;
③?ABCD中,AB=BC,根据一组邻边相等的平行四边形是菱形,即可判定?ABCD是菱形;故③正确;
D、?ABCD中,AC=BD,根据对角线相等的平行四边形是矩形,即可判定?ABCD是矩形,而不能判定?ABCD是菱形;故④错误.
故选:A.
6.B
【详解】A、如图,∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,
∵BE=DF,∴OE=OF,∴四边形AECF是平行四边形,故不符合题意;
B、如图所示,AE=CF,不能得到四边形AECF是平行四边形,故符合题意;
C、如图,∵四边形ABCD是平行四边形,∴OA=OC,
∵AF//CE,∴∠FAO=∠ECO,
又∵∠AOF=∠COE,∴△AOF≌△COE,∴AF=CE,
∴AFfalse CE,∴四边形AECF是平行四边形,故不符合题意;
D、如图,∵四边形ABCD是平行四边形,∴AB=CD,AB//CD,
∴∠ABE=∠CDF,
又∵∠BAE=∠DCF,∴△ABE≌△CDF,∴AE=CF,∠AEB=∠CFD,∴∠AEO=∠CFO,
∴AE//CF,
∴AEfalse CF,∴四边形AECF是平行四边形,故不符合题意,
故选B.
7.C
解:∵四边形ABCD是平行四边形,
∴BD=2BO,AD=BC,
∵BD=2AD,
∴BD=2BC,
∴BO=BC,
∵E为OC中点,
∴BE⊥AC,故①成立;
∵BE⊥AC,G是AB中点,
∴EG=falseAB,
∵E、F分别是OC、OD的中点,
∴EF∥CD,且EF=falseCD,
∵四边形ABCD为平行四边形,
∴AB∥CD,且AB=CD,
∴EF=falseAB,
∴EF=EG,故②成立;
∵AB∥CD,EF∥CD,
∴EF∥AB,
∴∠FEG=∠BGE(两直线平行,内错角相等),
在△EFG和△GBE中,
∵BG=FE,∠FEG=∠BGE,GE=EG,
∴△EFG≌△GBE(SAS),即③成立;
∵BG=FE,EF∥AB,
∴四边形BEFG是平行四边形,
∵BE⊥AC,
∴GF⊥AC,
∵EF=EG,
∴∠AEG=∠AEF,
即EA平分∠GEF
故④正确,
若四边形BEFG是菱形
∴BE=BG=falseAB,
∴∠BAC=30°
与题意不符合
故⑤错误
故选C.
8.C
详解:如图,连接CF,
∵点D是BC中点,
∴BD=CD,
由折叠知,∠ACB=∠DFE,CD=DF,
∴BD=CD=DF,
∴△BFC是直角三角形,
∴∠BFC=90°,
∵BD=DF,
∴∠B=∠BFD,
∴∠EAF=∠B+∠ACB=∠BFD+∠DFE=∠AFE,
∴AE=EF,故A正确,
由折叠知,EF=CE,
∴AE=CE,
∵BD=CD,
∴DE是△ABC的中位线,
∴AB=2DE,故B正确,
∵AE=CE,
∴S△ADE=S△CDE,
由折叠知,△CDE≌△△FDE,
∴S△CDE=S△FDE,
∴S△ADE=S△FDE,故D正确,
∴C选项不正确,
故选:C.
9.B
解:false四边形ABCD是平行四边形,
∴AD//BC,AD=BC,
A、∵AE=CF,
∴DE=BF,
∴四边形BFDE是平行四边形,
∴BE//DF,故本选项能判定BE//DF;
B、∵BE=DF,
false四边形BFDE是等腰梯形,
false本选项不一定能判定BE//DF;
C、∵AD//BC,
∴∠BED+∠EBF=180°,∠EDF+∠BFD=180°,
∵∠EBF=∠FDE,
∴∠BED=∠BFD,
false四边形BFDE是平行四边形,
∴BE//DF,
故本选项能判定BE//DF;
D、∵AD//BC,
∴∠BED+∠EBF=180°,∠EDF+∠BFD=180°,
∵∠BED=∠BFD,
∴∠EBF=∠FDE,
∴四边形BFDE是平行四边形,
∴BE//DF,故本选项能判定BE//DF.
故选:B.
10.B
解:∵四边形ABCD是平行四边形,
∴OA=OC,
∵AE=EB,
∴OE=falseBC,
∵AE+EO=4,
∴2AE+2EO=8,
∴AB+BC=8,
∴平行四边形ABCD的周长=2×8=16,
故选:B.
11.3false
【详解】∵四边形ABCD是矩形,∴∠D=90°,BC=AD=3,
∵将矩形ABCD绕点A逆时针旋转得到矩形AEFG,
∴EF=BC=3,AE=AB,
∵DE=EF,
∴AD=DE=3,
∴AE=false=3false,
∴AB=3false,
故答案为:3false.
12.8
【详解】∵四边形ACDF是正方形,
∴AC=FA,∠CAF=90°,
∴∠CAE+∠FAB=90°,
∵∠CEA=90°,∴∠CAE+∠ACE=90°,
∴∠ACE=∠FAB,
又∵∠AEC=∠FBA=90°,
∴△AEC≌△FBA,
∴CE=AB=4,
∴S阴影=12AB·CE=8,
故答案为:8.
13.4
解:如图,设AC与BD的交点为O,连接PO,
∵四边形ABCD是矩形
∴AO=CO=5=BO=DO,
∴S△DCO=falseS矩形ABCD=10,
∵S△DCO=S△DPO+S△PCO,
∴10=false×DO×PF+false×OC×PE
∴20=5PF+5PE
∴PE+PF=4
故答案为:4
14.(-2false,6)
详解:连接OB1,作B1H⊥OA于H,
由题意得,OA=6,AB=OC-2false,
则tan∠BOA=false,
∴∠BOA=30°,
∴∠OBA=60°,
由旋转的性质可知,∠B1OB=∠BOA=30°,
∴∠B1OH=60°,
在△AOB和△HB1O,
false,
∴△AOB≌△HB1O,
∴B1H=OA=6,OH=AB=2false,
∴点B1的坐标为(-2false,6),
故答案为:(-2false,6).
15.100°
解:∵FN∥DC,
∴∠BNF=∠C=80°,
∵△BMN沿MN翻折得△FMN,
∴∠BMN=∠FMN=40°,
∠BNM=false∠BNF=false×80°=40°,
在△BMN中,∠B=180°﹣(∠BMN+∠BNM)=180°﹣(40°+40°)=180°﹣80°=100°.
故答案为:100°.
16.证明见解析.
详解:∵四边形ABCD是平行四边形,
∴OA=OC,OD=OB,
∵AE=CF,
∴OE=OF,
在△BEO和△DFO中,false,
∴△BEO≌△DFO,
∴BE=DF.
17.(1)证明见解析;(2)2.
详解:(1)证明:∵false∥false,
∴false
∵false平分false
∴false,
∴false
∴false
又∵false
∴false
又∵false∥false,
∴四边形false是平行四边形
又∵false
∴false是菱形
(2)解:∵四边形false是菱形,对角线false、false交于点false.
∴false.false,false,
∴false.
在false中,false.
∴false.
∵false,
∴false.
在false中,false.false为false中点.
∴false.
18.(1)证明见解析;(2)AB=13cm,
【详解】(1)∵D、E分别是AB、AC的中点,F是BC延长线上的一点,
∴ED是Rt△ABC的中位线,
∴ED∥FC.BC=2DE,
又 EF∥DC,
∴四边形CDEF是平行四边形;
(2)∵四边形CDEF是平行四边形;
∴DC=EF,
∵DC是Rt△ABC斜边AB上的中线,
∴AB=2DC,
∴四边形DCFE的周长=AB+BC,
∵四边形DCFE的周长为25cm,AC的长5cm,
∴BC=25﹣AB,
∵在Rt△ABC中,∠ACB=90°,
∴AB2=BC2+AC2,即AB2=(25﹣AB)2+52,
解得,AB=13cm.
19.(1)证明见解析;(2)BC=2CD,理由见解析.
详解:(1)∵四边形ABCD是矩形,
∴AB∥CD,
∴∠FAE=∠CDE,
∵E是AD的中点,
∴AE=DE,
又∵∠FEA=∠CED,
∴△FAE≌△CDE,
∴CD=FA,
又∵CD∥AF,
∴四边形ACDF是平行四边形;
(2)BC=2CD.
证明:∵CF平分∠BCD,
∴∠DCE=45°,
∵∠CDE=90°,
∴△CDE是等腰直角三角形,
∴CD=DE,
∵E是AD的中点,
∴AD=2CD,
∵AD=BC,
∴BC=2CD.
