第二十九章 投影与视图专题训练(含解析)
文档属性
| 名称 | 第二十九章 投影与视图专题训练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 355.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-18 12:42:19 | ||
图片预览


文档简介
人教版九年级下册第二十九章投影与视图专题训练
学校:___________姓名:___________班级:___________考号:___________
一、单选题
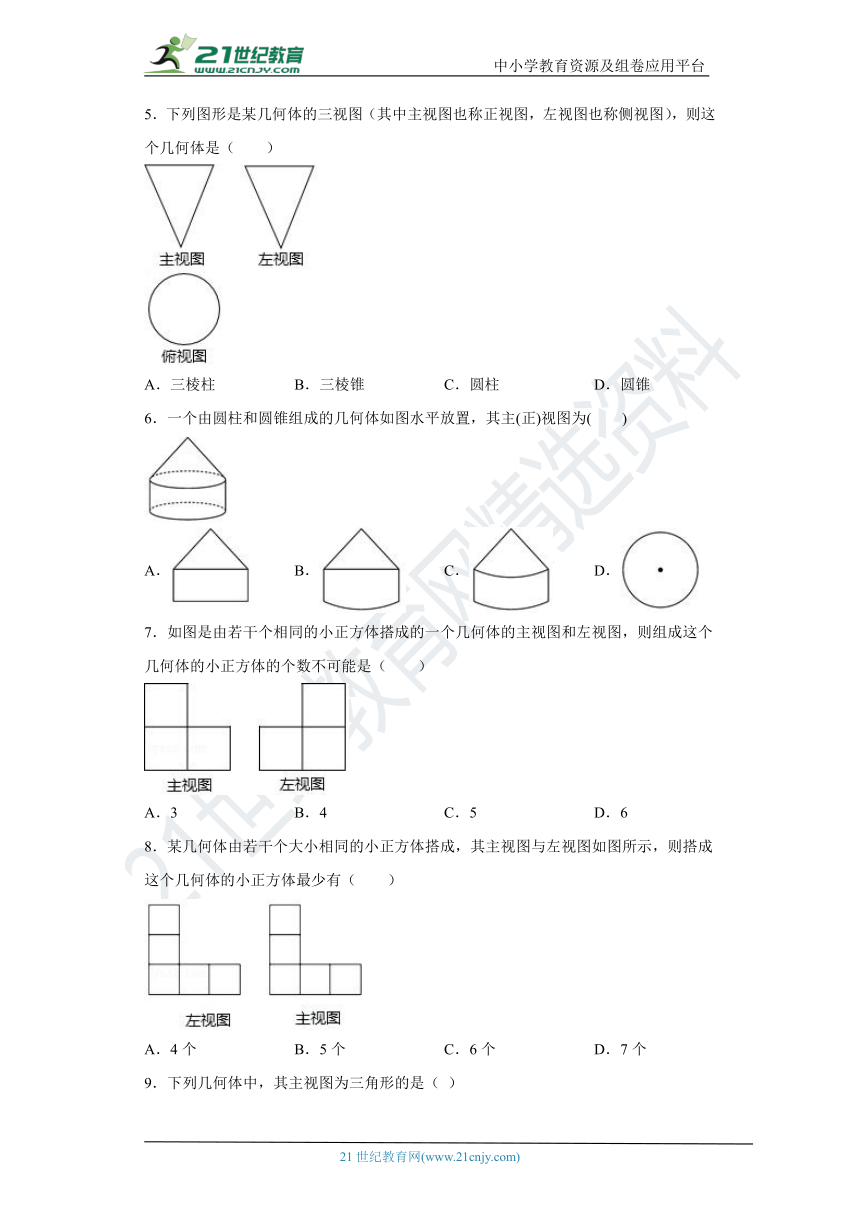
1.由一些相同的小立方块搭成的几何体的三视图如图所示,则搭成该几何体的小立方块有( )
A.3块 B.4块 C.6块 D.9块
2.如图是由三个相同的小正方体组成的几何体,则该几何体的左视图是( )
A. B. C. D.
3.如图是由6个大小相同的立方体组成的几何体,在这个几何体的三视图中,是中心对称图形的是false false
A.主视图 B.左视图 C.俯视图 D.主视图和左视图
4.圆锥的主视图与左视图都是边长为4的等边三角形,则圆锥的侧面展开图扇形的圆心角是( )
A.90° B.120° C.150° D.180°
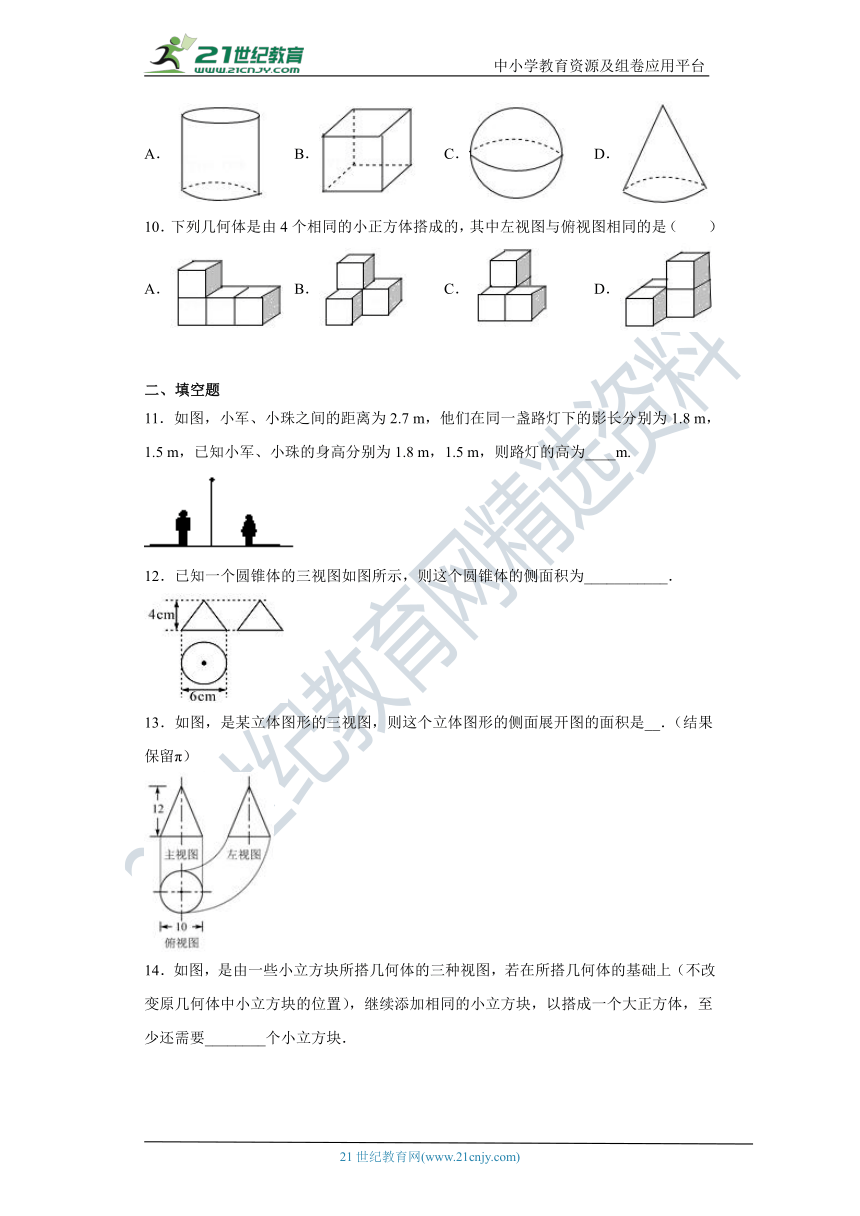
5.下列图形是某几何体的三视图(其中主视图也称正视图,左视图也称侧视图),则这个几何体是( )
A.三棱柱 B.三棱锥 C.圆柱 D.圆锥
6.一个由圆柱和圆锥组成的几何体如图水平放置,其主(正)视图为( )
A. B. C. D.
7.如图是由若干个相同的小正方体搭成的一个几何体的主视图和左视图,则组成这个几何体的小正方体的个数不可能是( )
A.3 B.4 C.5 D.6
8.某几何体由若干个大小相同的小正方体搭成,其主视图与左视图如图所示,则搭成这个几何体的小正方体最少有( )
A.4个 B.5个 C.6个 D.7个
9.下列几何体中,其主视图为三角形的是( )
A. B. C. D.
10.下列几何体是由4个相同的小正方体搭成的,其中左视图与俯视图相同的是( )
A. B. C. D.
二、填空题
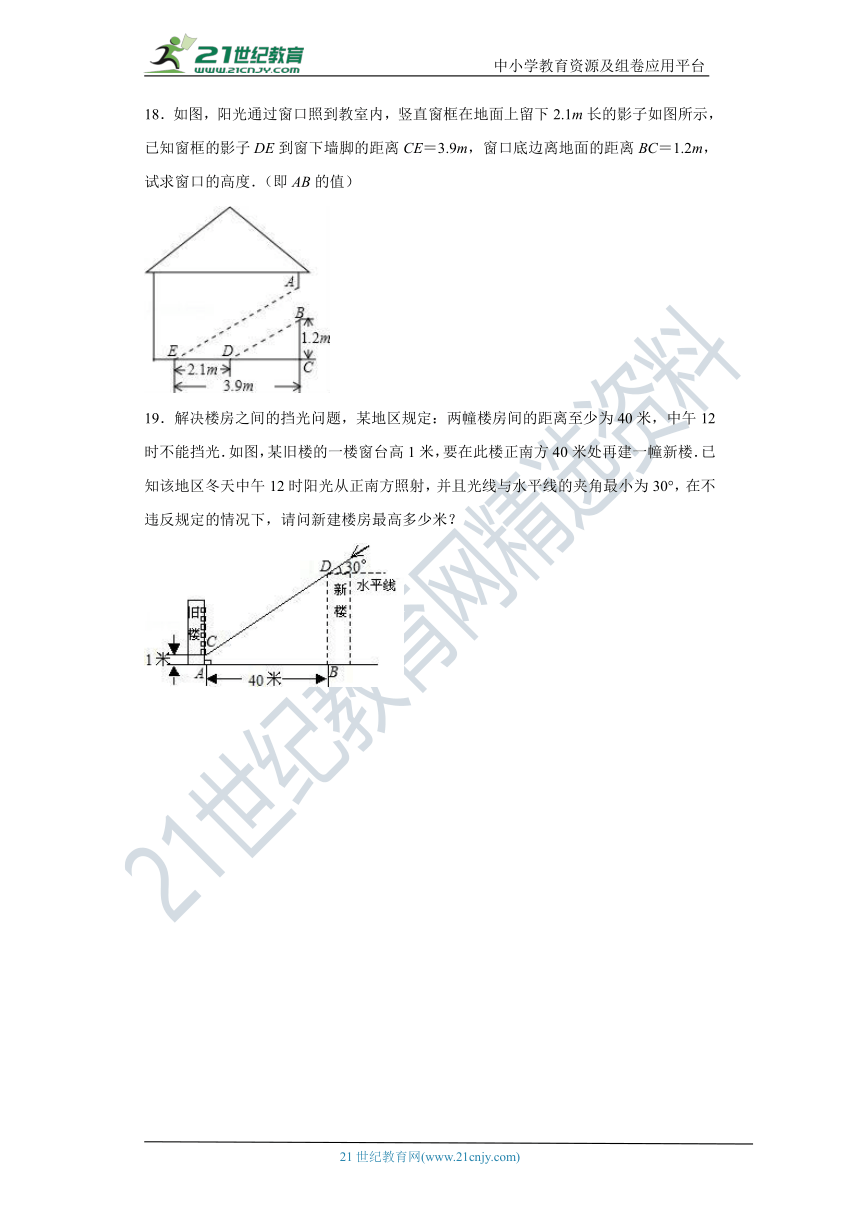
11.如图,小军、小珠之间的距离为2.7 m,他们在同一盏路灯下的影长分别为1.8 m,1.5 m,已知小军、小珠的身高分别为1.8 m,1.5 m,则路灯的高为____m.
12.已知一个圆锥体的三视图如图所示,则这个圆锥体的侧面积为___________.
13.如图,是某立体图形的三视图,则这个立体图形的侧面展开图的面积是__.(结果保留π)
14.如图,是由一些小立方块所搭几何体的三种视图,若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个大正方体,至少还需要________个小立方块.
15.几个相同的正方形叠合在一起,该组合的正视图(即从正面看到的图形)和俯视图(即从上面看到的图形)如下所示,那么组合体中的正方体的个数至少为__________,最多__________个.
三、解答题
16.(2017四川省达州市)如图,信号塔PQ座落在坡度i=1:2的山坡上,其正前方直立着一警示牌.当太阳光线与水平线成60°角时,测得信号塔PQ落在斜坡上的影子QN长为false米,落在警示牌上的影子MN长为3米,求信号塔PQ的高.(结果不取近似值)
17.如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.
(1)请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子.
(2)如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.
18.如图,阳光通过窗口照到教室内,竖直窗框在地面上留下2.1m长的影子如图所示,已知窗框的影子DE到窗下墙脚的距离CE=3.9m,窗口底边离地面的距离BC=1.2m,试求窗口的高度.(即AB的值)
19.解决楼房之间的挡光问题,某地区规定:两幢楼房间的距离至少为40米,中午12时不能挡光.如图,某旧楼的一楼窗台高1米,要在此楼正南方40米处再建一幢新楼.已知该地区冬天中午12时阳光从正南方照射,并且光线与水平线的夹角最小为30°,在不违反规定的情况下,请问新建楼房最高多少米?
参考答案
1.B
解:从俯视图可得最底层有3个小正方体,由主视图可得有2层上面一层是1个小正方体,下面有2个小正方体,从左视图上看,后面一层是2个小正方体,前面有1个小正方体,所以此几何体共有四个正方体.
故选B.
2.C
解:从左边看竖直叠放2个正方形.
故选:C.
3.C
解:观察几何体,可得三视图如图所示:
可知俯视图是中心对称图形,
故选C.
4.D
解:∵圆锥的主视图与左视图都是边长为4的等边三角形,
∴圆锥的母线长为4、底面圆的直径为4,
则圆锥的侧面展开图扇形的半径为4,
设圆锥的侧面展开图扇形的圆心角是n,
根据题意,得:false=4π,
解得:n=180°,
故选D.
5.D
解:由主视图以及左视图可知这是一个锥体,再根据俯视图可知是一个圆锥,
所以此几何体是一个圆锥,
故选D.
6.A
解:观察实物,可知这个几何体的主视图为长方体上面一个三角形,
只有A选项符合题意,
故选A.
7.D
解:左视图与主视图相同,可判断出底面最少有2个,最多有4个小正方体,而第二层则只有1个小正方体,
则这个几何体的小立方块可能有3或4或5个.
故选D.
8.B
解:由主视图和左视图可确定所需正方体个数最少时俯视图(数字为该位置小正方体的个数)为:
则搭成这个几何体的小正方体最少有5个,
故选B.
9.D
试题分析:A.圆柱的主视图为矩形,∴A不符合题意;
B.正方体的主视图为正方形,∴B不符合题意;
C.球体的主视图为圆形,∴C不符合题意;
D.圆锥的主视图为三角形,∴D符合题意.
故选D.
10.C
试题分析:从物体的前面向后面投射所得的视图称主视图(正视图)——能反映物体的前面形状;从物体的上面向下面投射所得的视图称俯视图——能反映物体的上面形状;从物体的左面向右面投射所得的视图称左视图——能反映物体的左面形状。选项C左视图与俯视图都是,故选C.
11.3
试题分析:如图,∵CD∥AB∥MN,
∴△ABE∽△CDE,△ABF∽△MNF,
∴false,
即false,
解得:AB=3m,
答:路灯的高为3m.
12.falsecm2
【解析】根据三视图得到圆锥的底面圆的直径为6cm,即底面圆的半径为3cm,圆锥的高为4cm,
所以圆锥的母线长=false =5,所以这个圆锥的侧面积=π×3×5=15π(cm2).
故答案为:15πcm2.
13.65π
解:由三视图可知圆锥的底面半径为5,高为12,所以母线长为13,
所以侧面积为πrl=π×5×13=65π,
故答案为:65π.
14.54
试题解析:由主视图可知,搭成的几何体有三层,且有4列;由左视图可知,搭成的几何体共有3行;
第一层有7个正方体,第二层有2个正方体,第三层有1个正方体,
共有10个正方体,
∵搭在这个几何体的基础上添加相同大小的小正方体,以搭成一个大正方体,
∴搭成的大正方体的共有4×4×4=64个小正方体,
∴至少还需要64-10=54个小正方体.
15.8 10
解:第一层有1+2+3=6个正方体,第二层最少有2个正方体,所以这个几何体最少有8个正方体组成;
第一层有1+2+3=6个正方体,第二层最多有4个正方体,所以这个几何体最多有10个正方体组成.
故答案为8,10.
16.false.
【试题解析】如图作false于false于E,则四边形EMFQ是矩形.
在false中,设false,则false,
false,
false,
false,
false,
false,
false,
false,
在false中,false,
false.??
17.(1)画图见解析;(2)DE=4.
试题解析:(1)解:如图,点O为灯泡所在的位置,线段FH为小亮在灯光下形成的影子.
(2)解:由已知可得,false,∴false,∴OD=4m,∴灯泡的高为4m.
18.窗口的高度为1.4m
试题解析:由于阳光是平行光线,即AE∥BD,………1分
所以∠AEC=∠BDC. 又因为∠C是公共角,
所以△AEC∽△BDC,从而有.………3分
又AC=AB+BC,DC=EC-ED,EC=3.9,ED=2.1,BC=1.2,
于是有,
解得 AB=1.4(m)。.………5分
答:窗口的高度为1.4m。.………6分
19.false米
解:过点C作CE⊥BD于E.
∵AB=40米,
∴CE=40米,
∵阳光入射角为30°,
∴∠DCE=30°,
在Rt△DCE中tan∠DCE=false.
∴false,
∴DE=40×false米,
∵AC=BE=1米,
∴DB=BE+ED=1+false米.
答:新建楼房最高为false米.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.由一些相同的小立方块搭成的几何体的三视图如图所示,则搭成该几何体的小立方块有( )
A.3块 B.4块 C.6块 D.9块
2.如图是由三个相同的小正方体组成的几何体,则该几何体的左视图是( )
A. B. C. D.
3.如图是由6个大小相同的立方体组成的几何体,在这个几何体的三视图中,是中心对称图形的是false false
A.主视图 B.左视图 C.俯视图 D.主视图和左视图
4.圆锥的主视图与左视图都是边长为4的等边三角形,则圆锥的侧面展开图扇形的圆心角是( )
A.90° B.120° C.150° D.180°
5.下列图形是某几何体的三视图(其中主视图也称正视图,左视图也称侧视图),则这个几何体是( )
A.三棱柱 B.三棱锥 C.圆柱 D.圆锥
6.一个由圆柱和圆锥组成的几何体如图水平放置,其主(正)视图为( )
A. B. C. D.
7.如图是由若干个相同的小正方体搭成的一个几何体的主视图和左视图,则组成这个几何体的小正方体的个数不可能是( )
A.3 B.4 C.5 D.6
8.某几何体由若干个大小相同的小正方体搭成,其主视图与左视图如图所示,则搭成这个几何体的小正方体最少有( )
A.4个 B.5个 C.6个 D.7个
9.下列几何体中,其主视图为三角形的是( )
A. B. C. D.
10.下列几何体是由4个相同的小正方体搭成的,其中左视图与俯视图相同的是( )
A. B. C. D.
二、填空题
11.如图,小军、小珠之间的距离为2.7 m,他们在同一盏路灯下的影长分别为1.8 m,1.5 m,已知小军、小珠的身高分别为1.8 m,1.5 m,则路灯的高为____m.
12.已知一个圆锥体的三视图如图所示,则这个圆锥体的侧面积为___________.
13.如图,是某立体图形的三视图,则这个立体图形的侧面展开图的面积是__.(结果保留π)
14.如图,是由一些小立方块所搭几何体的三种视图,若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个大正方体,至少还需要________个小立方块.
15.几个相同的正方形叠合在一起,该组合的正视图(即从正面看到的图形)和俯视图(即从上面看到的图形)如下所示,那么组合体中的正方体的个数至少为__________,最多__________个.
三、解答题
16.(2017四川省达州市)如图,信号塔PQ座落在坡度i=1:2的山坡上,其正前方直立着一警示牌.当太阳光线与水平线成60°角时,测得信号塔PQ落在斜坡上的影子QN长为false米,落在警示牌上的影子MN长为3米,求信号塔PQ的高.(结果不取近似值)
17.如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.
(1)请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子.
(2)如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.
18.如图,阳光通过窗口照到教室内,竖直窗框在地面上留下2.1m长的影子如图所示,已知窗框的影子DE到窗下墙脚的距离CE=3.9m,窗口底边离地面的距离BC=1.2m,试求窗口的高度.(即AB的值)
19.解决楼房之间的挡光问题,某地区规定:两幢楼房间的距离至少为40米,中午12时不能挡光.如图,某旧楼的一楼窗台高1米,要在此楼正南方40米处再建一幢新楼.已知该地区冬天中午12时阳光从正南方照射,并且光线与水平线的夹角最小为30°,在不违反规定的情况下,请问新建楼房最高多少米?
参考答案
1.B
解:从俯视图可得最底层有3个小正方体,由主视图可得有2层上面一层是1个小正方体,下面有2个小正方体,从左视图上看,后面一层是2个小正方体,前面有1个小正方体,所以此几何体共有四个正方体.
故选B.
2.C
解:从左边看竖直叠放2个正方形.
故选:C.
3.C
解:观察几何体,可得三视图如图所示:
可知俯视图是中心对称图形,
故选C.
4.D
解:∵圆锥的主视图与左视图都是边长为4的等边三角形,
∴圆锥的母线长为4、底面圆的直径为4,
则圆锥的侧面展开图扇形的半径为4,
设圆锥的侧面展开图扇形的圆心角是n,
根据题意,得:false=4π,
解得:n=180°,
故选D.
5.D
解:由主视图以及左视图可知这是一个锥体,再根据俯视图可知是一个圆锥,
所以此几何体是一个圆锥,
故选D.
6.A
解:观察实物,可知这个几何体的主视图为长方体上面一个三角形,
只有A选项符合题意,
故选A.
7.D
解:左视图与主视图相同,可判断出底面最少有2个,最多有4个小正方体,而第二层则只有1个小正方体,
则这个几何体的小立方块可能有3或4或5个.
故选D.
8.B
解:由主视图和左视图可确定所需正方体个数最少时俯视图(数字为该位置小正方体的个数)为:
则搭成这个几何体的小正方体最少有5个,
故选B.
9.D
试题分析:A.圆柱的主视图为矩形,∴A不符合题意;
B.正方体的主视图为正方形,∴B不符合题意;
C.球体的主视图为圆形,∴C不符合题意;
D.圆锥的主视图为三角形,∴D符合题意.
故选D.
10.C
试题分析:从物体的前面向后面投射所得的视图称主视图(正视图)——能反映物体的前面形状;从物体的上面向下面投射所得的视图称俯视图——能反映物体的上面形状;从物体的左面向右面投射所得的视图称左视图——能反映物体的左面形状。选项C左视图与俯视图都是,故选C.
11.3
试题分析:如图,∵CD∥AB∥MN,
∴△ABE∽△CDE,△ABF∽△MNF,
∴false,
即false,
解得:AB=3m,
答:路灯的高为3m.
12.falsecm2
【解析】根据三视图得到圆锥的底面圆的直径为6cm,即底面圆的半径为3cm,圆锥的高为4cm,
所以圆锥的母线长=false =5,所以这个圆锥的侧面积=π×3×5=15π(cm2).
故答案为:15πcm2.
13.65π
解:由三视图可知圆锥的底面半径为5,高为12,所以母线长为13,
所以侧面积为πrl=π×5×13=65π,
故答案为:65π.
14.54
试题解析:由主视图可知,搭成的几何体有三层,且有4列;由左视图可知,搭成的几何体共有3行;
第一层有7个正方体,第二层有2个正方体,第三层有1个正方体,
共有10个正方体,
∵搭在这个几何体的基础上添加相同大小的小正方体,以搭成一个大正方体,
∴搭成的大正方体的共有4×4×4=64个小正方体,
∴至少还需要64-10=54个小正方体.
15.8 10
解:第一层有1+2+3=6个正方体,第二层最少有2个正方体,所以这个几何体最少有8个正方体组成;
第一层有1+2+3=6个正方体,第二层最多有4个正方体,所以这个几何体最多有10个正方体组成.
故答案为8,10.
16.false.
【试题解析】如图作false于false于E,则四边形EMFQ是矩形.
在false中,设false,则false,
false,
false,
false,
false,
false,
false,
false,
在false中,false,
false.??
17.(1)画图见解析;(2)DE=4.
试题解析:(1)解:如图,点O为灯泡所在的位置,线段FH为小亮在灯光下形成的影子.
(2)解:由已知可得,false,∴false,∴OD=4m,∴灯泡的高为4m.
18.窗口的高度为1.4m
试题解析:由于阳光是平行光线,即AE∥BD,………1分
所以∠AEC=∠BDC. 又因为∠C是公共角,
所以△AEC∽△BDC,从而有.………3分
又AC=AB+BC,DC=EC-ED,EC=3.9,ED=2.1,BC=1.2,
于是有,
解得 AB=1.4(m)。.………5分
答:窗口的高度为1.4m。.………6分
19.false米
解:过点C作CE⊥BD于E.
∵AB=40米,
∴CE=40米,
∵阳光入射角为30°,
∴∠DCE=30°,
在Rt△DCE中tan∠DCE=false.
∴false,
∴DE=40×false米,
∵AC=BE=1米,
∴DB=BE+ED=1+false米.
答:新建楼房最高为false米.
