第二十七章 相似专题训练(含解析)
图片预览




文档简介
人教版九年级下册第二十七章相似专题训练
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,在平行四边形ABCD中,E是DC上的点,DE:EC=3:2,连接AE交BD于点F,则△DEF与△BAF的面积之比为( )
A.2:5 B.3:5 C.9:25 D.4:25
2.如图,在false中,点false、false分别在边false、false上,false平分false,false,与false一定相似的三角形为( )
A.false B.false C.false D.false
3.如图,等边△ABC的边长为3,P为BC上一点,且BP=1,D为AC上一点,若∠APD=60°,则CD的长是( )
A.false B.false C.false D.false
4.如图,在△ABC中,EF∥BC,AB=3AE,若S四边形BCFE=16,则S△ABC=( )
A.16 B.18 C.20 D.24
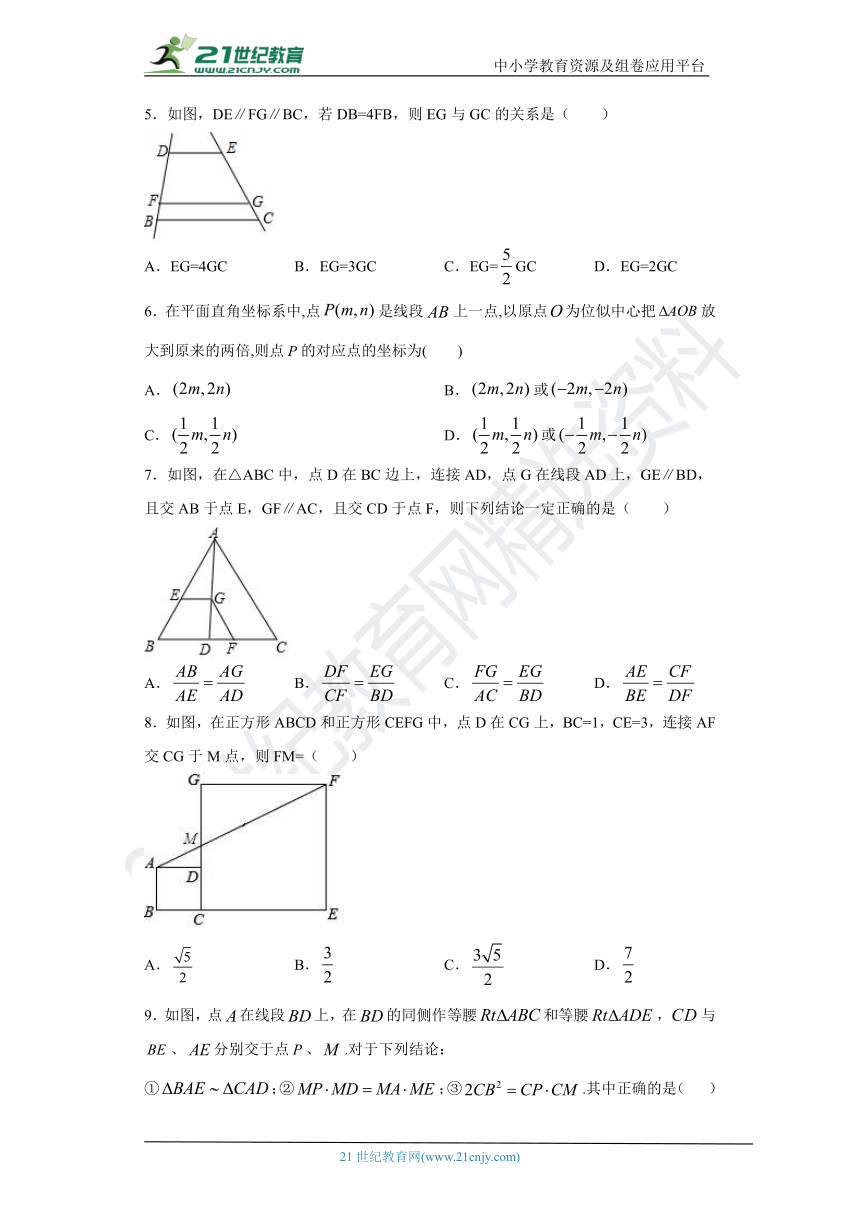
5.如图,DE∥FG∥BC,若DB=4FB,则EG与GC的关系是( )
A.EG=4GC B.EG=3GC C.EG=falseGC D.EG=2GC
6.在平面直角坐标系中,点false是线段false上一点,以原点false为位似中心把false放大到原来的两倍,则点false的对应点的坐标为( )
A.false B.false或false
C.false D.false或false
7.如图,在△ABC中,点D在BC边上,连接AD,点G在线段AD上,GE∥BD,且交AB于点E,GF∥AC,且交CD于点F,则下列结论一定正确的是( )
A.false B.false C.false D.false
8.如图,在正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,连接AF交CG于M点,则FM=( )
A.false B.false C.false D.false
9.如图,点false在线段false上,在false的同侧作等腰false和等腰false,false与false、false分别交于点false、false.对于下列结论:
①false;②false;③false.其中正确的是( )
A.①②③ B.① C.①② D.②③
10.制作一块3m×2m长方形广告牌的成本是120元,在每平方米制作成本相同的情况下,若将此广告牌的四边都扩大为原来的3倍,那么扩大后长方形广告牌的成本是( )
A.360元 B.720元 C.1080元 D.2160元
二、填空题
11.如图,已知正方形DEFG的顶点D、E在△ABC的边BC上,顶点G、F分别在边AB、AC上.如果BC=4,△ABC的面积是6,那么这个正方形的边长是_____.
12.如图,在矩形false中,false是边false的中点,连接false交对角线false于点false,若false,false,则false的长为________.
13.已知false,且false,则false的值为__________.
14.如图,EF是△ABC的中位线,将△AEF沿AB方向平移到△EBO的位置,点D在BC上,已知△AEF的面积为5,则图中阴影部分的面积为________.
15.矩形ABCD中,AB=6,BC=8.点P在矩形ABCD的内部,点E在边BC上,满足△PBE∽△DBC,若△APD是等腰三角形,则PE的长为数___________.
三、解答题
16.如图,O是△ABC的外心,I是△ABC的内心,连AI并延长交BC和⊙O于D、E两点.
(1)求证:EB=EI;
(2)若AB=4,AC=3,BE=2,求AI的长.
17.如图,在正方形ABCD中,点E,F分别是边AD,BC的中点,连接DF,过点E作EH⊥DF,垂足为H,EH的延长线交DC于点G.
(1)猜想DG与CF的数量关系,并证明你的结论;
(2)过点H作MN∥CD,分别交AD,BC于点M,N,若正方形ABCD的边长为10,点P是MN上一点,求△PDC周长的最小值.
18.如图,AD是△ABC的外接圆⊙O的直径,点P在BC延长线上,且满足∠PAC=∠B.
(1)求证:PA是⊙O的切线;
(2)弦CE⊥AD交AB于点F,若AF?AB=12 ,求AC的长.
19.如图,在正方形false中,false是false上一点,连接false.过点false作false,垂足为false.false经过点false、false、false,与false相交于点false.
(1)求证false;
(2)若正方形false的边长为false,false,求false的半径.
参考答案
1.C
解:∵四边形ABCD为平行四边形,
∴CD∥AB,
∴△DEF∽△BAF.
∵DE:EC=3:2,
∴false,
∴false.
故选:C.
2.B
解:false平分false,
false
false,
false
又false
false,且false
false
故选false.
3.C
解:∵△ABC为等边三角形,
∴∠B=∠C=60°,
又∵∠APD+∠DPC=∠B+∠BAP,且∠APD=60°,
∴∠BAP=∠DPC,
∴△ABP∽△PCD,
∴false,
∵AB=BC=3,BP=1,
∴PC=2,
∴false,
∴CD=false,
故选C.
4.B
【详解】∵EF∥BC,
∴△AEF∽△ABC,
∵AB=3AE,
∴AE:AB=1:3,
∴S△AEF:S△ABC=1:9,
设S△AEF=x,
∵S四边形BCFE=16,
∴false,
解得:x=2,
∴S△ABC=18,
故选B.
5.B
解:∵DE∥FG∥BC,DB=4FB,
∴false=3.
故选:B.
6.B
解:点P(m,n)是线段AB上一点,以原点O为位似中心把△AOB放大到原来的两倍,
则点P的对应点的坐标为(m×2,n×2)或(m×(-2),n×(-2)),即(2m,2n)或(-2m,-2n),
故选B.
7.D
解:∵GE∥BD,GF∥AC,
∴△AEG∽△ABD,△DFG∽△DCA,
∴false,false,
∴false.
故选:D.
8.C
解:∵四边形ABCD和四边形CEFG是正方形,
∴AD=CD=BC=1、CE=CG=GF=3,∠ADM=∠G=90°,
∴DG=CG﹣CD=2,AD∥GF,
则△ADM∽△FGM,
∴false,即false,
解得:GM=false,
∴FM=false,
故选:C.
9.A
解:由已知:AC=falseAB,AD=falseAE
∴false
∵∠BAC=∠EAD
∴∠BAE=∠CAD
∴△BAE∽△CAD
所以①正确
∵△BAE∽△CAD
∴∠BEA=∠CDA
∵∠PME=∠AMD
∴△PME∽△AMD
∴false
∴MP?MD=MA?ME
所以②正确
∵∠BEA=∠CDA
∠PME=∠AMD
∴P、E、D、A四点共圆
∴∠APD=∠EAD=90°
∵∠CAE=180°-∠BAC-∠EAD=90°
∴△CAP∽△CMA
∴AC2=CP?CM
∵AC=falseAB
∴2CB2=CP?CM
所以③正确
故选A.
10.C
解:3m×2m=6m2,
∴长方形广告牌的成本是120÷6=20元/m2,
将此广告牌的四边都扩大为原来的3倍,
则面积扩大为原来的9倍,
∴扩大后长方形广告牌的面积=9×6=54m2,
∴扩大后长方形广告牌的成本是54×20=1080元,
故选C.
11.false
解:作AH⊥BC于H,交GF于M,如图,
∵△ABC的面积是6,
∴falseBC?AH=6,
∴AH=false=3,
设正方形DEFG的边长为x,则GF=x,MH=x,AM=3﹣x,
∵GF∥BC,
∴△AGF∽△ABC,
∴false,即false,解得x=false,
即正方形DEFG的边长为false,
故答案为:false.
12.false
解:∵四边形false是矩形,∴false,false∥false,false,
在false中,false,∴false,
∵false是false中点,∴false,
∵false∥false,∴false,∴false.
故答案为:false.
13.12
解:∵false,
∴设a=6x,b=5x,c=4x,
∵a+b-2c=6,
∴6x+5x-8x=6,
解得:x=2,
故a=12.
故答案为:12.
14.10
解:∵EF是△ABC的中位线,∴EF∥BC,∴△AEF∽△ABC,
∴EF:BC=1:2,∴S△AEF :S△ABC =1:4,
∵△AEF的面积为5,∴S△ABC =20,
∵将△AEF沿AB方向平移到△EBD的位置,∴S△EBD =5,
∴图中阴影部分的面积为:S△ABC﹣S△EBD﹣S△AEF =20﹣5﹣5=10,
故答案为:10.
15.3或1.2
【详解】∵四边形ABCD是矩形,∴∠BAD=∠C=90°,CD=AB=6,∴BD=10,
∵△PBE∽△DBC,
∴∠PBE=∠DBC,∴点P在BD上,
如图1,当DP=DA=8时,BP=2,
∵△PBE∽△DBC,
∴PE:CD=PB:DB=2:10,
∴PE:6=2:10,
∴PE=1.2;
如图2,当AP=DP时,此时P为BD中点,
∵△PBE∽△DBC,
∴PE:CD=PB:DB=1:2,
∴PE:6=1:2,
∴PE=3;
综上,PE的长为1.2或3,
故答案为:1.2或3.
16.(1)见解析;(2)AI=2.
详解:(1)连BI.如图,
∵I是△ABC的内心,
∴∠BAE=∠CAE,∠ABI=∠CBI,
∵∠CBE=∠CAE,
∴∠BAE=∠CBE,
∴∠BIE=∠ABI+∠BAE,∠IBE=∠CBI+∠CBE,
∴∠IBE=∠BIE,
∴EB=EI.
(2)设AI=x,由(1)可知:∠BAE=∠CBE,且∠E=∠E.
∴△BDE∽△ABE,BE2=ED·EA,即: DE=false.
又∵∠E=∠C(同弦的圆周角相等),∠BAE=∠CAE.
∴△ADC∽△ABE,AB·AC=AD·AE,
4×3=(x+2)(false),
解得x=2,即AI=2.
17.(1)结论:CF=2DG,理由见解析;(2)△PCD的周长的最小值为10+2false.
解:(1)结论:CF=2DG.
理由:∵四边形ABCD是正方形,
∴AD=BC=CD=AB,∠ADC=∠C=90°,
∵DE=AE,
∴AD=CD=2DE,
∵EG⊥DF,
∴∠DHG=90°,
∴∠CDF+∠DGE=90°,∠DGE+∠DEG=90°,
∴∠CDF=∠DEG,
∴△DEG∽△CDF,
∴false=false=false,
∴CF=2DG.
(2)作点C关于NM的对称点K,连接DK交MN于点P,连接PC,
此时△PDC的周长最短.周长的最小值=CD+PD+PC=CD+PD+PK=CD+DK.
由题意:CD=AD=10,ED=AE=5,DG=false,EG=false,DH=false=false,
∴EH=2DH=2false,
∴HM=false=2,
∴DM=CN=NK=false=1,
在Rt△DCK中,DK=false=false=2false,
∴△PCD的周长的最小值为10+2false.
18.(1)见解析;(2)AC=2false.
解:(1)false是false的直径
false;
false
false,false,
false,
false,
false,
false点false在false上,
false是false的切线
(2)false,
false,
false,
false,
false,
false,
false,
false false,
false
false,
false,
false.
19.(1)证明见解析;(2)false
详解:(1)证明:在正方形false中,false.
∴false.
∵false.
∴false.
∴false.
∴false.
∵四边形false是false的内接四边形,
∴false.
又false,
∴false.
∴false.
(2)解:如图,连接false.
∵false,false,
∴false.
∴false,即false.
∵false,
∴false.
∴false.
在正方形false中,false,
∴false,false.
∴false.
∵false,
∴false是false的直径.
∴false的半径为false.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,在平行四边形ABCD中,E是DC上的点,DE:EC=3:2,连接AE交BD于点F,则△DEF与△BAF的面积之比为( )
A.2:5 B.3:5 C.9:25 D.4:25
2.如图,在false中,点false、false分别在边false、false上,false平分false,false,与false一定相似的三角形为( )
A.false B.false C.false D.false
3.如图,等边△ABC的边长为3,P为BC上一点,且BP=1,D为AC上一点,若∠APD=60°,则CD的长是( )
A.false B.false C.false D.false
4.如图,在△ABC中,EF∥BC,AB=3AE,若S四边形BCFE=16,则S△ABC=( )
A.16 B.18 C.20 D.24
5.如图,DE∥FG∥BC,若DB=4FB,则EG与GC的关系是( )
A.EG=4GC B.EG=3GC C.EG=falseGC D.EG=2GC
6.在平面直角坐标系中,点false是线段false上一点,以原点false为位似中心把false放大到原来的两倍,则点false的对应点的坐标为( )
A.false B.false或false
C.false D.false或false
7.如图,在△ABC中,点D在BC边上,连接AD,点G在线段AD上,GE∥BD,且交AB于点E,GF∥AC,且交CD于点F,则下列结论一定正确的是( )
A.false B.false C.false D.false
8.如图,在正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,连接AF交CG于M点,则FM=( )
A.false B.false C.false D.false
9.如图,点false在线段false上,在false的同侧作等腰false和等腰false,false与false、false分别交于点false、false.对于下列结论:
①false;②false;③false.其中正确的是( )
A.①②③ B.① C.①② D.②③
10.制作一块3m×2m长方形广告牌的成本是120元,在每平方米制作成本相同的情况下,若将此广告牌的四边都扩大为原来的3倍,那么扩大后长方形广告牌的成本是( )
A.360元 B.720元 C.1080元 D.2160元
二、填空题
11.如图,已知正方形DEFG的顶点D、E在△ABC的边BC上,顶点G、F分别在边AB、AC上.如果BC=4,△ABC的面积是6,那么这个正方形的边长是_____.
12.如图,在矩形false中,false是边false的中点,连接false交对角线false于点false,若false,false,则false的长为________.
13.已知false,且false,则false的值为__________.
14.如图,EF是△ABC的中位线,将△AEF沿AB方向平移到△EBO的位置,点D在BC上,已知△AEF的面积为5,则图中阴影部分的面积为________.
15.矩形ABCD中,AB=6,BC=8.点P在矩形ABCD的内部,点E在边BC上,满足△PBE∽△DBC,若△APD是等腰三角形,则PE的长为数___________.
三、解答题
16.如图,O是△ABC的外心,I是△ABC的内心,连AI并延长交BC和⊙O于D、E两点.
(1)求证:EB=EI;
(2)若AB=4,AC=3,BE=2,求AI的长.
17.如图,在正方形ABCD中,点E,F分别是边AD,BC的中点,连接DF,过点E作EH⊥DF,垂足为H,EH的延长线交DC于点G.
(1)猜想DG与CF的数量关系,并证明你的结论;
(2)过点H作MN∥CD,分别交AD,BC于点M,N,若正方形ABCD的边长为10,点P是MN上一点,求△PDC周长的最小值.
18.如图,AD是△ABC的外接圆⊙O的直径,点P在BC延长线上,且满足∠PAC=∠B.
(1)求证:PA是⊙O的切线;
(2)弦CE⊥AD交AB于点F,若AF?AB=12 ,求AC的长.
19.如图,在正方形false中,false是false上一点,连接false.过点false作false,垂足为false.false经过点false、false、false,与false相交于点false.
(1)求证false;
(2)若正方形false的边长为false,false,求false的半径.
参考答案
1.C
解:∵四边形ABCD为平行四边形,
∴CD∥AB,
∴△DEF∽△BAF.
∵DE:EC=3:2,
∴false,
∴false.
故选:C.
2.B
解:false平分false,
false
false,
false
又false
false,且false
false
故选false.
3.C
解:∵△ABC为等边三角形,
∴∠B=∠C=60°,
又∵∠APD+∠DPC=∠B+∠BAP,且∠APD=60°,
∴∠BAP=∠DPC,
∴△ABP∽△PCD,
∴false,
∵AB=BC=3,BP=1,
∴PC=2,
∴false,
∴CD=false,
故选C.
4.B
【详解】∵EF∥BC,
∴△AEF∽△ABC,
∵AB=3AE,
∴AE:AB=1:3,
∴S△AEF:S△ABC=1:9,
设S△AEF=x,
∵S四边形BCFE=16,
∴false,
解得:x=2,
∴S△ABC=18,
故选B.
5.B
解:∵DE∥FG∥BC,DB=4FB,
∴false=3.
故选:B.
6.B
解:点P(m,n)是线段AB上一点,以原点O为位似中心把△AOB放大到原来的两倍,
则点P的对应点的坐标为(m×2,n×2)或(m×(-2),n×(-2)),即(2m,2n)或(-2m,-2n),
故选B.
7.D
解:∵GE∥BD,GF∥AC,
∴△AEG∽△ABD,△DFG∽△DCA,
∴false,false,
∴false.
故选:D.
8.C
解:∵四边形ABCD和四边形CEFG是正方形,
∴AD=CD=BC=1、CE=CG=GF=3,∠ADM=∠G=90°,
∴DG=CG﹣CD=2,AD∥GF,
则△ADM∽△FGM,
∴false,即false,
解得:GM=false,
∴FM=false,
故选:C.
9.A
解:由已知:AC=falseAB,AD=falseAE
∴false
∵∠BAC=∠EAD
∴∠BAE=∠CAD
∴△BAE∽△CAD
所以①正确
∵△BAE∽△CAD
∴∠BEA=∠CDA
∵∠PME=∠AMD
∴△PME∽△AMD
∴false
∴MP?MD=MA?ME
所以②正确
∵∠BEA=∠CDA
∠PME=∠AMD
∴P、E、D、A四点共圆
∴∠APD=∠EAD=90°
∵∠CAE=180°-∠BAC-∠EAD=90°
∴△CAP∽△CMA
∴AC2=CP?CM
∵AC=falseAB
∴2CB2=CP?CM
所以③正确
故选A.
10.C
解:3m×2m=6m2,
∴长方形广告牌的成本是120÷6=20元/m2,
将此广告牌的四边都扩大为原来的3倍,
则面积扩大为原来的9倍,
∴扩大后长方形广告牌的面积=9×6=54m2,
∴扩大后长方形广告牌的成本是54×20=1080元,
故选C.
11.false
解:作AH⊥BC于H,交GF于M,如图,
∵△ABC的面积是6,
∴falseBC?AH=6,
∴AH=false=3,
设正方形DEFG的边长为x,则GF=x,MH=x,AM=3﹣x,
∵GF∥BC,
∴△AGF∽△ABC,
∴false,即false,解得x=false,
即正方形DEFG的边长为false,
故答案为:false.
12.false
解:∵四边形false是矩形,∴false,false∥false,false,
在false中,false,∴false,
∵false是false中点,∴false,
∵false∥false,∴false,∴false.
故答案为:false.
13.12
解:∵false,
∴设a=6x,b=5x,c=4x,
∵a+b-2c=6,
∴6x+5x-8x=6,
解得:x=2,
故a=12.
故答案为:12.
14.10
解:∵EF是△ABC的中位线,∴EF∥BC,∴△AEF∽△ABC,
∴EF:BC=1:2,∴S△AEF :S△ABC =1:4,
∵△AEF的面积为5,∴S△ABC =20,
∵将△AEF沿AB方向平移到△EBD的位置,∴S△EBD =5,
∴图中阴影部分的面积为:S△ABC﹣S△EBD﹣S△AEF =20﹣5﹣5=10,
故答案为:10.
15.3或1.2
【详解】∵四边形ABCD是矩形,∴∠BAD=∠C=90°,CD=AB=6,∴BD=10,
∵△PBE∽△DBC,
∴∠PBE=∠DBC,∴点P在BD上,
如图1,当DP=DA=8时,BP=2,
∵△PBE∽△DBC,
∴PE:CD=PB:DB=2:10,
∴PE:6=2:10,
∴PE=1.2;
如图2,当AP=DP时,此时P为BD中点,
∵△PBE∽△DBC,
∴PE:CD=PB:DB=1:2,
∴PE:6=1:2,
∴PE=3;
综上,PE的长为1.2或3,
故答案为:1.2或3.
16.(1)见解析;(2)AI=2.
详解:(1)连BI.如图,
∵I是△ABC的内心,
∴∠BAE=∠CAE,∠ABI=∠CBI,
∵∠CBE=∠CAE,
∴∠BAE=∠CBE,
∴∠BIE=∠ABI+∠BAE,∠IBE=∠CBI+∠CBE,
∴∠IBE=∠BIE,
∴EB=EI.
(2)设AI=x,由(1)可知:∠BAE=∠CBE,且∠E=∠E.
∴△BDE∽△ABE,BE2=ED·EA,即: DE=false.
又∵∠E=∠C(同弦的圆周角相等),∠BAE=∠CAE.
∴△ADC∽△ABE,AB·AC=AD·AE,
4×3=(x+2)(false),
解得x=2,即AI=2.
17.(1)结论:CF=2DG,理由见解析;(2)△PCD的周长的最小值为10+2false.
解:(1)结论:CF=2DG.
理由:∵四边形ABCD是正方形,
∴AD=BC=CD=AB,∠ADC=∠C=90°,
∵DE=AE,
∴AD=CD=2DE,
∵EG⊥DF,
∴∠DHG=90°,
∴∠CDF+∠DGE=90°,∠DGE+∠DEG=90°,
∴∠CDF=∠DEG,
∴△DEG∽△CDF,
∴false=false=false,
∴CF=2DG.
(2)作点C关于NM的对称点K,连接DK交MN于点P,连接PC,
此时△PDC的周长最短.周长的最小值=CD+PD+PC=CD+PD+PK=CD+DK.
由题意:CD=AD=10,ED=AE=5,DG=false,EG=false,DH=false=false,
∴EH=2DH=2false,
∴HM=false=2,
∴DM=CN=NK=false=1,
在Rt△DCK中,DK=false=false=2false,
∴△PCD的周长的最小值为10+2false.
18.(1)见解析;(2)AC=2false.
解:(1)false是false的直径
false;
false
false,false,
false,
false,
false,
false点false在false上,
false是false的切线
(2)false,
false,
false,
false,
false,
false,
false,
false false,
false
false,
false,
false.
19.(1)证明见解析;(2)false
详解:(1)证明:在正方形false中,false.
∴false.
∵false.
∴false.
∴false.
∴false.
∵四边形false是false的内接四边形,
∴false.
又false,
∴false.
∴false.
(2)解:如图,连接false.
∵false,false,
∴false.
∴false,即false.
∵false,
∴false.
∴false.
在正方形false中,false,
∴false,false.
∴false.
∵false,
∴false是false的直径.
∴false的半径为false.
