高考二轮复习之两角和与差的正弦、余弦和正切公式(Word解析版)
文档属性
| 名称 | 高考二轮复习之两角和与差的正弦、余弦和正切公式(Word解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 44.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-18 19:36:34 | ||
图片预览

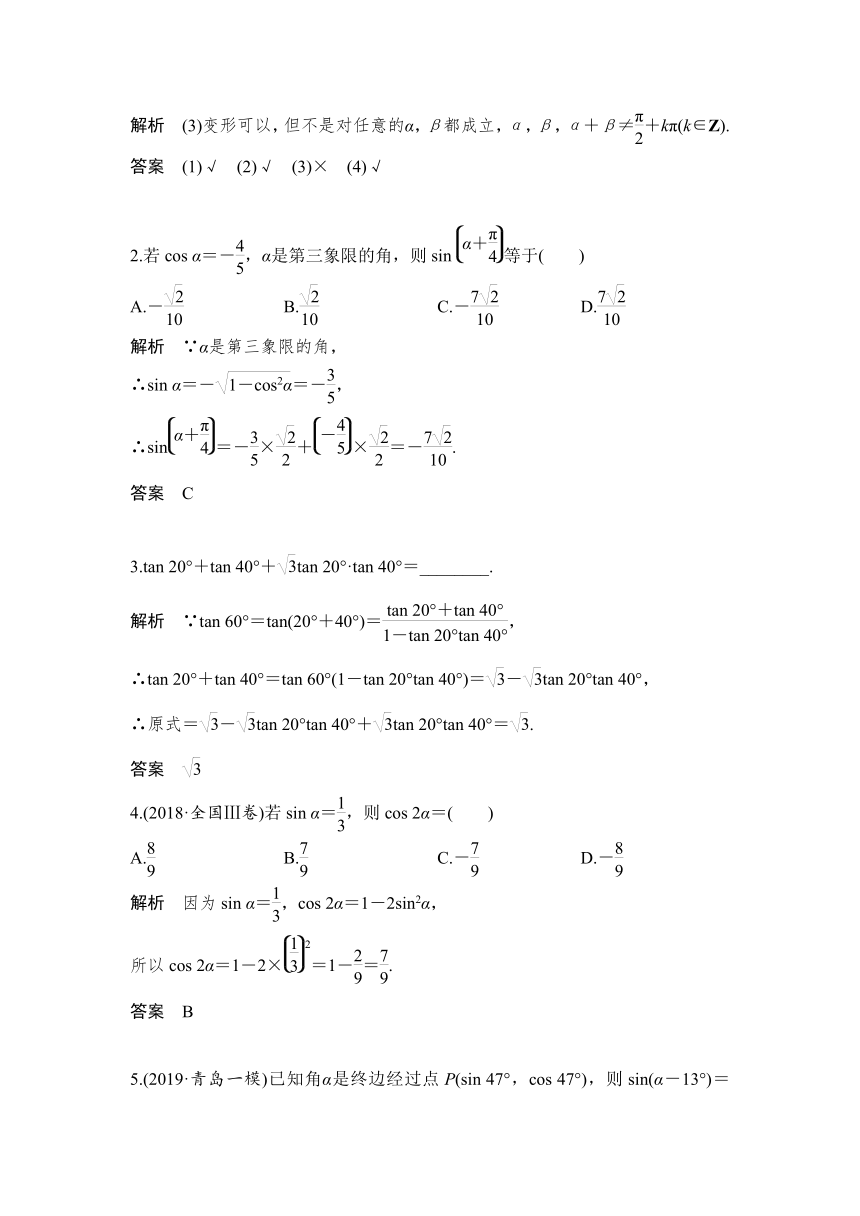



文档简介
导数的概念及运算
一、知识梳理
1.两角和与差的正弦、余弦和正切公式
sin(α±β)=sinαcosβ±cosαsinβ.
cos(α?β)=cosαcosβ±sinαsinβ.
tan(α±β)=.
2.二倍角的正弦、余弦、正切公式
sin
2α=2sinαcosα.
cos
2α=cos2α-sin2α=2cos2α-1=1-2sin2α.
tan
2α=.
3.函数f(α)=asin
α+bcos
α(a,b为常数),可以化为f(α)=sin(α+φ)或f(α)=·cos(α-φ).
总结:
1.tan
α±tan
β=tan(α±β)(1?tanαtan
β).
2.cos2α=,sin2α=.
3.1+sin
2α=(sin
α+cos
α)2,1-sin
2α=(sin
α-cos
α)2,
sin
α±cos
α=sin.
二、例题精讲
+
随堂练习
1.判断下列结论正误(在括号内打“√”或“×”)
(1)两角和与差的正弦、余弦公式中的角α,β是任意的.( )
(2)存在实数α,β,使等式sin(α+β)=sin
α+sin
β成立.( )
(3)公式tan(α+β)=可以变形为tan
α+tan
β
=tan(α+β)(1-tan
αtan
β),且对任意角α,β都成立.( )
(4)存在实数α,使tan
2α=2tan
α.( )
解析 (3)变形可以,但不是对任意的α,β都成立,α,β,α+β≠+kπ(k∈Z).
答案 (1)√ (2)√ (3)× (4)√
2.若cos
α=-,α是第三象限的角,则sin等于( )
A.-
B.
C.-
D.
解析 ∵α是第三象限的角,
∴sin
α=-=-,
∴sin=-×+×=-.
答案 C
3.tan
20°+tan
40°+tan
20°·tan
40°=________.
解析 ∵tan
60°=tan(20°+40°)=,
∴tan
20°+tan
40°=tan
60°(1-tan
20°tan
40°)=-tan
20°tan
40°,
∴原式=-tan
20°tan
40°+tan
20°tan
40°=.
答案
4.(2018·全国Ⅲ卷)若sin
α=,则cos
2α=( )
A.
B.
C.-
D.-
解析 因为sin
α=,cos
2α=1-2sin2α,
所以cos
2α=1-2×=1-=.
答案 B
5.(2019·青岛一模)已知角α是终边经过点P(sin
47°,cos
47°),则sin(α-13°)=( )
A.
B.
C.-
D.-
解析 由三角函数定义,sin
α=cos
47°,cos
α=sin
47°,
则sin(α-13°)=sin
αcos
13°-cos
αsin
13°
=cos
47°cos
13°-sin
47°sin
13°
=cos(47°+13°)=cos
60°=.
答案 A
6.(2018·全国Ⅱ卷)已知sin
α+cos
β=1,cos
α+sin
β=0,则sin(α+β)=________.
解析 由sin
α+cos
β=1,cos
α+sin
β=0,
两式平方相加,得2+2sin
αcos
β+2cos
αsin
β=1,
整理得sin(α+β)=-.
答案 -
考点一 三角函数式的化简
【例1】
(1)化简:sin(α+β)cos(γ-β)-cos(β+α)sin(β-γ)=________.
(2)化简:(0<α<π)=________.
解析 (1)sin(α+β)cos(γ-β)-cos(β+α)sin(β-γ)
=sin(α+β)cos
(β-γ)-cos(α+β)sin(β-γ)
=sin[(α+β)-(β-γ)]=sin(α+γ).
(2)原式=
==.
因为0<α<π,所以0<<,所以cos>0,所以原式=cos
α.
答案 (1)sin(α+γ) (2)cos
α
【训练1】
(1)cos(α+β)cos
β+sin(α+β)sin
β=( )
A.sin(α+2β)
B.sin
α
C.cos(α+2β)
D.cos
α
(2)化简:=________.
解析 (1)cos(α+β)cos
β+sin(α+β)sin
β=cos[(α+β)-β]=cos
α.
(2)原式=
==
==cos
2α.
答案 (1)D (2)cos
2α
考点二 三角函数式的求值
角度1 给角(值)求值
【例2-1】
(1)计算:=________.
解析 ====.
答案
(2)(2018·江苏卷)已知α,β为锐角,tan
α=,cos(α+β)=-.
①求cos
2α的值;
②求tan(α-β)的值.
解 ①因为tan
α=,tan
α=,
所以sin
α=cos
α.
因为sin2α+cos2α=1,所以cos2α=,
因此,cos
2α=2cos2α-1=-.
②因为α,β为锐角,所以α+β∈(0,π).
又因为cos(α+β)=-,
所以sin(α+β)==,
因此tan(α+β)=-2.
因为tan
α=,所以tan
2α==-,
因此,tan(α-β)=tan[2α-(α+β)]==-.
角度2 给值求角
【例2-2】
(1)(2019·河南六市联考)已知cos
α=,cos(α-β)=,若0<β<α<,则β=________.
(2)已知α,β∈(0,π),且tan(α-β)=,tan
β=-,则2α-β的值为________.
解析 (1)由cos
α=,0<α<,
得sin
α===.
由0<β<α<,得0<α-β<,又cos(α-β)=,
∴sin(α-β)===.
由β=α-(α-β)得cos
β=cos[α-(α-β)]
=cos
αcos(α-β)+sin
αsin(α-β)=×+×=.
∵β∈,∴β=.
(2)∵tan
α=tan[(α-β)+β]=
==>0,
又α∈(0,π),∴0<α<,
又∵tan
2α===>0,
∴0<2α<,
∴tan(2α-β)===1.
∵tan
β=-<0,∴<β<π,-π<2α-β<0,∴2α-β=-.
答案 (1) (2)-
【训练2】
(1)(2019·天津河西区模拟)tan
70°·cos
10°(tan
20°-1)等于( )
A.1
B.2
C.-1
D.-2
(2)已知α,β为锐角,cos
α=,且sin(α+β)=,则角β=________.
(3)若=·sin
2θ,则sin
2θ=( )
A.
B.
C.-
D.-
解析 (1)tan
70°·cos
10°(tan
20°-1)=·cos
10°
=·===-1.
(2)∵α为锐角,且cos
α=,∴sin
α==.
∵α,β∈,∴0<α+β<π.又∵sin(α+β)α,∴α+β>,
∴cos(α+β)=-.cos
β=cos[(α+β)-α]=cos(α+β)cos
α+sin(α+β)sin
α
=-×+×==.
∴β=.
(3)由题意知=sin
2θ,
∴2(cos
θ+sin
θ)=sin
2θ,则4(1+sin
2θ)=3sin22θ,
因此sin
2θ=-或sin
2θ=2(舍).
答案 (1)C (2) (3)C
考点三 三角恒等变换的简单应用
【例3】
(2019·杭州模拟)设函数f(x)=sin2ωx-cos2ωx+2sin
ωxcos
ωx+λ的图象关于直线x=π对称,其中ω,λ为常数,且ω∈.
(1)求函数f(x)的最小正周期;
(2)若y=f(x)的图象经过点,求函数f(x)在区间上的最值.
解 (1)f(x)=sin2ωx+2sin
ωx·cos
ωx-cos2ωx+λ
=sin
2ωx-cos
2ωx+λ
=2sin+λ,
因为图象关于直线x=π对称,
所以2πω-=+kπ(k∈Z),
所以ω=+(k∈Z),又ω∈,
令k=1时,ω=符合要求,
所以函数f(x)的最小正周期为=.
(2)因为f=0,
所以2sin+λ=0,则λ=-.
所以f(x)=2sin-.
由0≤x≤π,知-≤x-≤π,
∴当x-=-,即x=0时,f(x)取最小值-1-.
当x-=,即x=π时,f(x)取最大值2-.
【训练3】
(2017·北京卷)已知函数f(x)=cos-2sin
xcos
x.
(1)求f(x)的最小正周期;
(2)求证:当x∈时,f(x)≥-.
(1)解 f(x)=cos-2sin
xcos
x
=cos
2x+sin
2x-sin
2x
=sin
2x+cos
2x=sin,
所以f(x)的最小正周期T==π.
(2)证明 由(1)知f(x)=sin
.
∵x∈,∴2x+∈,
∴当2x+=-,即x=-时,f(x)取得最小值-.
∴f(x)≥-成立.
逻辑推理与数学运算——缩小角的范围常用策略
在运用平方关系和由三角函数值求角时都要注意角的范围.如果条件中角的范围恰好能够使用,那么就能顺势求解题目.但绝大部分题目都会设置一定的障碍,特别是角的范围,往往所给的范围较大,需要根据条件缩小范围.
类型1 由三角函数值的符号缩小角的范围
【例1】
已知α,β∈(0,π),tan
α=2,cos
β=-,求2α-β的值.
解 法一 因为tan
α=2>0,α∈(0,π),所以α∈.
同理可得β∈,且tan
β=-.
所以α-β∈(-π,0),tan(α-β)==3>0,所以α-β∈,
所以2α-β∈(-π,0).
又tan(2α-β)=tan[α+(α-β)]==-1,所以2α-β=-.
法二 因为tan
α=2>1,α∈(0,π),所以α∈.
因为cos
β=-,β∈(0,π),所以β∈,
所以2α-β∈.
因为tan(2α-β)=tan[α+(α-β)]==-1,
所以2α-β=-.
类型2 由三角函数值及特殊角的三角函数值缩小范围
【例2】
设α,β∈(0,π),sin(α+β)=,tan
=,则cos
β=________.
解析 因为tan
=,
所以sin
α=2sin
cos
===,cos
α=cos2-sin2===∈.
又α∈(0,π),所以a∈,又β∈(0,π),所以α+β∈.又sin(α+β)=∈,所以α+β∈,所以cos(α+β)=-,所以cos
β=cos[(α+β)-α]=cos(α+β)cos
α+sin(α+β)sin
α=-.
答案 -
三、课后练习
1.若点(θ,0)是函数f(x)=sin
x+2cos
x图象的一个对称中心,则cos
2θ+sin
θcosθ=( )
A.
B.-
C.1
D.-1
解析 ∵点(θ,0)是函数f(x)=sin
x+2cos
x图象的一个对称中心,
∴sin
θ+2cos
θ=0,即tan
θ=-2.
∴cos
2θ+sin
θcos
θ=
===-1.
答案 D
2.已知θ是第四象限角,且sin=,则tan=( )
A.
B.-
C.-
D.
解析 法一 ∵sin=×(sin
θ+cos
θ)=,
∴sin
θ+cos
θ=,①
∴2sin
θcos
θ=-.
∵θ是第四象限角,∴sin
θ<0,cos
θ>0,
∴sin
θ-cos
θ=-=-,②
由①②得sin
θ=-,cos
θ=,∴tan
θ=-,
∴tan==-.
法二 ∵+=,
∴sin=cos=,
又2kπ-<θ<2kπ(k∈Z),
∴2kπ-<θ+<2kπ+(k∈Z),
∴cos=,∴sin=,
∴tan==,
∴tan=-tan=-.
答案 B
3.(2019·广东七校联考)已知sin+cos
α=-,则cos=________.
解析 ∵sin+cos
α=-,
∴sin
α+cos
α=-,sin=-,
则sin=-.
故cos=sin=sin=-.
答案 -
4.(2019·烟台二中月考)已知函数f(x)=·cos(x+θ)为奇函数,且f=0,其中a∈R,θ∈(0,π).
(1)求a,θ的值;
(2)若α∈,f+coscos
2α=0,求cos
α-sin
α的值.
解 (1)因为f(x)=cos(x+θ)是奇函数,
所以cos(x+θ)=-cos,
化简、整理得,cos
xcos
θ=0,则有cos
θ=0,
由θ∈(0,π),得θ=,所以f(x)=-sin
x·.
由f=0,得-(a+1)=0,即a=-1.
(2)由(1)知f(x)=-sin
2x,
f+coscos
2α=0?sin=coscos
2α,
因为cos
2α=sin=sin=2sincos,
所以sin=cos2sin.
又α∈,所以sin=0或cos2=.由sin=0?α=,
所以cos
α-sin
α=cos
-sin
=-;由cos2=,<α+<,
得cos=-?(cos
α-sin
α)=-?cos
α-sin
α=-.
综上,cos
α-sin
α=-或cos
α-sin
α=-.
5.设α,β∈[0,π],且满足sin
αcos
β-cos
αsin
β=1,则sin(2α-β)+sin(α-2β)的取值范围为( )
A.[-,1]
B.[-1,]
C.[-1,1]
D.[1,]
解析 ∵sin
αcos
β-cos
αsin
β=1,∴sin(α-β)=1,
∵α,β∈[0,π],
∴α-β=,由?≤α≤π,
∴sin(2α-β)+sin(α-2β)=sin+sin(α-2α+π)=cos
α+sin
α=sin,∵≤α≤π,∴≤α+≤π,∴-1≤sin≤1,即所求的取值范围是[-1,1],故选C.
一、知识梳理
1.两角和与差的正弦、余弦和正切公式
sin(α±β)=sinαcosβ±cosαsinβ.
cos(α?β)=cosαcosβ±sinαsinβ.
tan(α±β)=.
2.二倍角的正弦、余弦、正切公式
sin
2α=2sinαcosα.
cos
2α=cos2α-sin2α=2cos2α-1=1-2sin2α.
tan
2α=.
3.函数f(α)=asin
α+bcos
α(a,b为常数),可以化为f(α)=sin(α+φ)或f(α)=·cos(α-φ).
总结:
1.tan
α±tan
β=tan(α±β)(1?tanαtan
β).
2.cos2α=,sin2α=.
3.1+sin
2α=(sin
α+cos
α)2,1-sin
2α=(sin
α-cos
α)2,
sin
α±cos
α=sin.
二、例题精讲
+
随堂练习
1.判断下列结论正误(在括号内打“√”或“×”)
(1)两角和与差的正弦、余弦公式中的角α,β是任意的.( )
(2)存在实数α,β,使等式sin(α+β)=sin
α+sin
β成立.( )
(3)公式tan(α+β)=可以变形为tan
α+tan
β
=tan(α+β)(1-tan
αtan
β),且对任意角α,β都成立.( )
(4)存在实数α,使tan
2α=2tan
α.( )
解析 (3)变形可以,但不是对任意的α,β都成立,α,β,α+β≠+kπ(k∈Z).
答案 (1)√ (2)√ (3)× (4)√
2.若cos
α=-,α是第三象限的角,则sin等于( )
A.-
B.
C.-
D.
解析 ∵α是第三象限的角,
∴sin
α=-=-,
∴sin=-×+×=-.
答案 C
3.tan
20°+tan
40°+tan
20°·tan
40°=________.
解析 ∵tan
60°=tan(20°+40°)=,
∴tan
20°+tan
40°=tan
60°(1-tan
20°tan
40°)=-tan
20°tan
40°,
∴原式=-tan
20°tan
40°+tan
20°tan
40°=.
答案
4.(2018·全国Ⅲ卷)若sin
α=,则cos
2α=( )
A.
B.
C.-
D.-
解析 因为sin
α=,cos
2α=1-2sin2α,
所以cos
2α=1-2×=1-=.
答案 B
5.(2019·青岛一模)已知角α是终边经过点P(sin
47°,cos
47°),则sin(α-13°)=( )
A.
B.
C.-
D.-
解析 由三角函数定义,sin
α=cos
47°,cos
α=sin
47°,
则sin(α-13°)=sin
αcos
13°-cos
αsin
13°
=cos
47°cos
13°-sin
47°sin
13°
=cos(47°+13°)=cos
60°=.
答案 A
6.(2018·全国Ⅱ卷)已知sin
α+cos
β=1,cos
α+sin
β=0,则sin(α+β)=________.
解析 由sin
α+cos
β=1,cos
α+sin
β=0,
两式平方相加,得2+2sin
αcos
β+2cos
αsin
β=1,
整理得sin(α+β)=-.
答案 -
考点一 三角函数式的化简
【例1】
(1)化简:sin(α+β)cos(γ-β)-cos(β+α)sin(β-γ)=________.
(2)化简:(0<α<π)=________.
解析 (1)sin(α+β)cos(γ-β)-cos(β+α)sin(β-γ)
=sin(α+β)cos
(β-γ)-cos(α+β)sin(β-γ)
=sin[(α+β)-(β-γ)]=sin(α+γ).
(2)原式=
==.
因为0<α<π,所以0<<,所以cos>0,所以原式=cos
α.
答案 (1)sin(α+γ) (2)cos
α
【训练1】
(1)cos(α+β)cos
β+sin(α+β)sin
β=( )
A.sin(α+2β)
B.sin
α
C.cos(α+2β)
D.cos
α
(2)化简:=________.
解析 (1)cos(α+β)cos
β+sin(α+β)sin
β=cos[(α+β)-β]=cos
α.
(2)原式=
==
==cos
2α.
答案 (1)D (2)cos
2α
考点二 三角函数式的求值
角度1 给角(值)求值
【例2-1】
(1)计算:=________.
解析 ====.
答案
(2)(2018·江苏卷)已知α,β为锐角,tan
α=,cos(α+β)=-.
①求cos
2α的值;
②求tan(α-β)的值.
解 ①因为tan
α=,tan
α=,
所以sin
α=cos
α.
因为sin2α+cos2α=1,所以cos2α=,
因此,cos
2α=2cos2α-1=-.
②因为α,β为锐角,所以α+β∈(0,π).
又因为cos(α+β)=-,
所以sin(α+β)==,
因此tan(α+β)=-2.
因为tan
α=,所以tan
2α==-,
因此,tan(α-β)=tan[2α-(α+β)]==-.
角度2 给值求角
【例2-2】
(1)(2019·河南六市联考)已知cos
α=,cos(α-β)=,若0<β<α<,则β=________.
(2)已知α,β∈(0,π),且tan(α-β)=,tan
β=-,则2α-β的值为________.
解析 (1)由cos
α=,0<α<,
得sin
α===.
由0<β<α<,得0<α-β<,又cos(α-β)=,
∴sin(α-β)===.
由β=α-(α-β)得cos
β=cos[α-(α-β)]
=cos
αcos(α-β)+sin
αsin(α-β)=×+×=.
∵β∈,∴β=.
(2)∵tan
α=tan[(α-β)+β]=
==>0,
又α∈(0,π),∴0<α<,
又∵tan
2α===>0,
∴0<2α<,
∴tan(2α-β)===1.
∵tan
β=-<0,∴<β<π,-π<2α-β<0,∴2α-β=-.
答案 (1) (2)-
【训练2】
(1)(2019·天津河西区模拟)tan
70°·cos
10°(tan
20°-1)等于( )
A.1
B.2
C.-1
D.-2
(2)已知α,β为锐角,cos
α=,且sin(α+β)=,则角β=________.
(3)若=·sin
2θ,则sin
2θ=( )
A.
B.
C.-
D.-
解析 (1)tan
70°·cos
10°(tan
20°-1)=·cos
10°
=·===-1.
(2)∵α为锐角,且cos
α=,∴sin
α==.
∵α,β∈,∴0<α+β<π.又∵sin(α+β)
∴cos(α+β)=-.cos
β=cos[(α+β)-α]=cos(α+β)cos
α+sin(α+β)sin
α
=-×+×==.
∴β=.
(3)由题意知=sin
2θ,
∴2(cos
θ+sin
θ)=sin
2θ,则4(1+sin
2θ)=3sin22θ,
因此sin
2θ=-或sin
2θ=2(舍).
答案 (1)C (2) (3)C
考点三 三角恒等变换的简单应用
【例3】
(2019·杭州模拟)设函数f(x)=sin2ωx-cos2ωx+2sin
ωxcos
ωx+λ的图象关于直线x=π对称,其中ω,λ为常数,且ω∈.
(1)求函数f(x)的最小正周期;
(2)若y=f(x)的图象经过点,求函数f(x)在区间上的最值.
解 (1)f(x)=sin2ωx+2sin
ωx·cos
ωx-cos2ωx+λ
=sin
2ωx-cos
2ωx+λ
=2sin+λ,
因为图象关于直线x=π对称,
所以2πω-=+kπ(k∈Z),
所以ω=+(k∈Z),又ω∈,
令k=1时,ω=符合要求,
所以函数f(x)的最小正周期为=.
(2)因为f=0,
所以2sin+λ=0,则λ=-.
所以f(x)=2sin-.
由0≤x≤π,知-≤x-≤π,
∴当x-=-,即x=0时,f(x)取最小值-1-.
当x-=,即x=π时,f(x)取最大值2-.
【训练3】
(2017·北京卷)已知函数f(x)=cos-2sin
xcos
x.
(1)求f(x)的最小正周期;
(2)求证:当x∈时,f(x)≥-.
(1)解 f(x)=cos-2sin
xcos
x
=cos
2x+sin
2x-sin
2x
=sin
2x+cos
2x=sin,
所以f(x)的最小正周期T==π.
(2)证明 由(1)知f(x)=sin
.
∵x∈,∴2x+∈,
∴当2x+=-,即x=-时,f(x)取得最小值-.
∴f(x)≥-成立.
逻辑推理与数学运算——缩小角的范围常用策略
在运用平方关系和由三角函数值求角时都要注意角的范围.如果条件中角的范围恰好能够使用,那么就能顺势求解题目.但绝大部分题目都会设置一定的障碍,特别是角的范围,往往所给的范围较大,需要根据条件缩小范围.
类型1 由三角函数值的符号缩小角的范围
【例1】
已知α,β∈(0,π),tan
α=2,cos
β=-,求2α-β的值.
解 法一 因为tan
α=2>0,α∈(0,π),所以α∈.
同理可得β∈,且tan
β=-.
所以α-β∈(-π,0),tan(α-β)==3>0,所以α-β∈,
所以2α-β∈(-π,0).
又tan(2α-β)=tan[α+(α-β)]==-1,所以2α-β=-.
法二 因为tan
α=2>1,α∈(0,π),所以α∈.
因为cos
β=-,β∈(0,π),所以β∈,
所以2α-β∈.
因为tan(2α-β)=tan[α+(α-β)]==-1,
所以2α-β=-.
类型2 由三角函数值及特殊角的三角函数值缩小范围
【例2】
设α,β∈(0,π),sin(α+β)=,tan
=,则cos
β=________.
解析 因为tan
=,
所以sin
α=2sin
cos
===,cos
α=cos2-sin2===∈.
又α∈(0,π),所以a∈,又β∈(0,π),所以α+β∈.又sin(α+β)=∈,所以α+β∈,所以cos(α+β)=-,所以cos
β=cos[(α+β)-α]=cos(α+β)cos
α+sin(α+β)sin
α=-.
答案 -
三、课后练习
1.若点(θ,0)是函数f(x)=sin
x+2cos
x图象的一个对称中心,则cos
2θ+sin
θcosθ=( )
A.
B.-
C.1
D.-1
解析 ∵点(θ,0)是函数f(x)=sin
x+2cos
x图象的一个对称中心,
∴sin
θ+2cos
θ=0,即tan
θ=-2.
∴cos
2θ+sin
θcos
θ=
===-1.
答案 D
2.已知θ是第四象限角,且sin=,则tan=( )
A.
B.-
C.-
D.
解析 法一 ∵sin=×(sin
θ+cos
θ)=,
∴sin
θ+cos
θ=,①
∴2sin
θcos
θ=-.
∵θ是第四象限角,∴sin
θ<0,cos
θ>0,
∴sin
θ-cos
θ=-=-,②
由①②得sin
θ=-,cos
θ=,∴tan
θ=-,
∴tan==-.
法二 ∵+=,
∴sin=cos=,
又2kπ-<θ<2kπ(k∈Z),
∴2kπ-<θ+<2kπ+(k∈Z),
∴cos=,∴sin=,
∴tan==,
∴tan=-tan=-.
答案 B
3.(2019·广东七校联考)已知sin+cos
α=-,则cos=________.
解析 ∵sin+cos
α=-,
∴sin
α+cos
α=-,sin=-,
则sin=-.
故cos=sin=sin=-.
答案 -
4.(2019·烟台二中月考)已知函数f(x)=·cos(x+θ)为奇函数,且f=0,其中a∈R,θ∈(0,π).
(1)求a,θ的值;
(2)若α∈,f+coscos
2α=0,求cos
α-sin
α的值.
解 (1)因为f(x)=cos(x+θ)是奇函数,
所以cos(x+θ)=-cos,
化简、整理得,cos
xcos
θ=0,则有cos
θ=0,
由θ∈(0,π),得θ=,所以f(x)=-sin
x·.
由f=0,得-(a+1)=0,即a=-1.
(2)由(1)知f(x)=-sin
2x,
f+coscos
2α=0?sin=coscos
2α,
因为cos
2α=sin=sin=2sincos,
所以sin=cos2sin.
又α∈,所以sin=0或cos2=.由sin=0?α=,
所以cos
α-sin
α=cos
-sin
=-;由cos2=,<α+<,
得cos=-?(cos
α-sin
α)=-?cos
α-sin
α=-.
综上,cos
α-sin
α=-或cos
α-sin
α=-.
5.设α,β∈[0,π],且满足sin
αcos
β-cos
αsin
β=1,则sin(2α-β)+sin(α-2β)的取值范围为( )
A.[-,1]
B.[-1,]
C.[-1,1]
D.[1,]
解析 ∵sin
αcos
β-cos
αsin
β=1,∴sin(α-β)=1,
∵α,β∈[0,π],
∴α-β=,由?≤α≤π,
∴sin(2α-β)+sin(α-2β)=sin+sin(α-2α+π)=cos
α+sin
α=sin,∵≤α≤π,∴≤α+≤π,∴-1≤sin≤1,即所求的取值范围是[-1,1],故选C.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
