7.2 探索平行线的性质同步训练(含解析)
文档属性
| 名称 | 7.2 探索平行线的性质同步训练(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-18 13:10:56 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
初中数学苏科版七年级下册
7.2
探索平行线的性质
同步训练
一、单选题(本大题共10题,每题3分,共30分)
1.如图,已知直线
,
,则
的度数为(???
)
A.????????????????????????????????????B.????????????????????????????????????C.????????????????????????????????????D.?
2.如图,直线
与直线
相交,已知
,则
的度数是(?
)
A.???????????????????????????????????????B.???????????????????????????????????????C.???????????????????????????????????????D.?
3.直线AB∥CD
,
∠B=23°,∠D=42°,则∠E=(??
)
A.?23°???????????????????????????????????????B.?42°???????????????????????????????????????C.?65°???????????????????????????????????????D.?19°
4.直线a、b、c在同一平面内,(1)如果a⊥b,b⊥c,那么a∥c;(2)如果a∥b,b∥c,c∥d,那么a∥d;(3)如果a∥b,b⊥c,那么a⊥c;(4)如果a与b相交,b与c相交,那么a与c相交.在上述四种说法中,正确的个数为( )
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
5.一个学员在广场上驾驶汽车,两次拐弯后,行驶的方向与原来的方向相同,这两次拐弯的角度可能是(???
)
A.?第一次向右拐
50°
,第二次向左拐130°??????????????B.?第一次向右拐
50°
,第二次向右拐130°
C.?第一次向左拐
50°
,第二次向左拐130°??????????????D.?第一次向左拐
30°
,第二次向右拐
30°
6.如图,已知直线l1∥l2
,
将一块直角三角板ABC按如图所示方式放置,若∠1=39°,则∠2等于(??
)
A.?39°???????????????????????????????????????B.?45°???????????????????????????????????????C.?50°???????????????????????????????????????D.?51°
7.如图,直线
,
,
交于一点,直线
,若
,
,则
的度数为
???
A.????????????????????????????????????????B.????????????????????????????????????????C.????????????????????????????????????????D.?
8.如图,∠BCD=90°,AB∥DE
,
若∠α=40°,则∠β的大小为(?
)
A.?150°????????????????????????????????????B.?140°????????????????????????????????????C.?130°????????????????????????????????????D.?120°
9.如图,
,
,
,垂足为
,图中与
互余的角有(?
)
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
10.如图,已知AB//CD,则
,
,
之间的等量关系为(??
)
A.??????????????????????????????????B.?
C.??????????????????????????????????D.?
二、填空题(本大题共8题,每题2分,共16分)
11.如图所示,直线a∥b,如果∠1=45°,那么∠2的度数是________.
12.如图,AB∥CD,∠FGB=150°,FG
平分∠EFD,则∠AEF
的度数于________°.
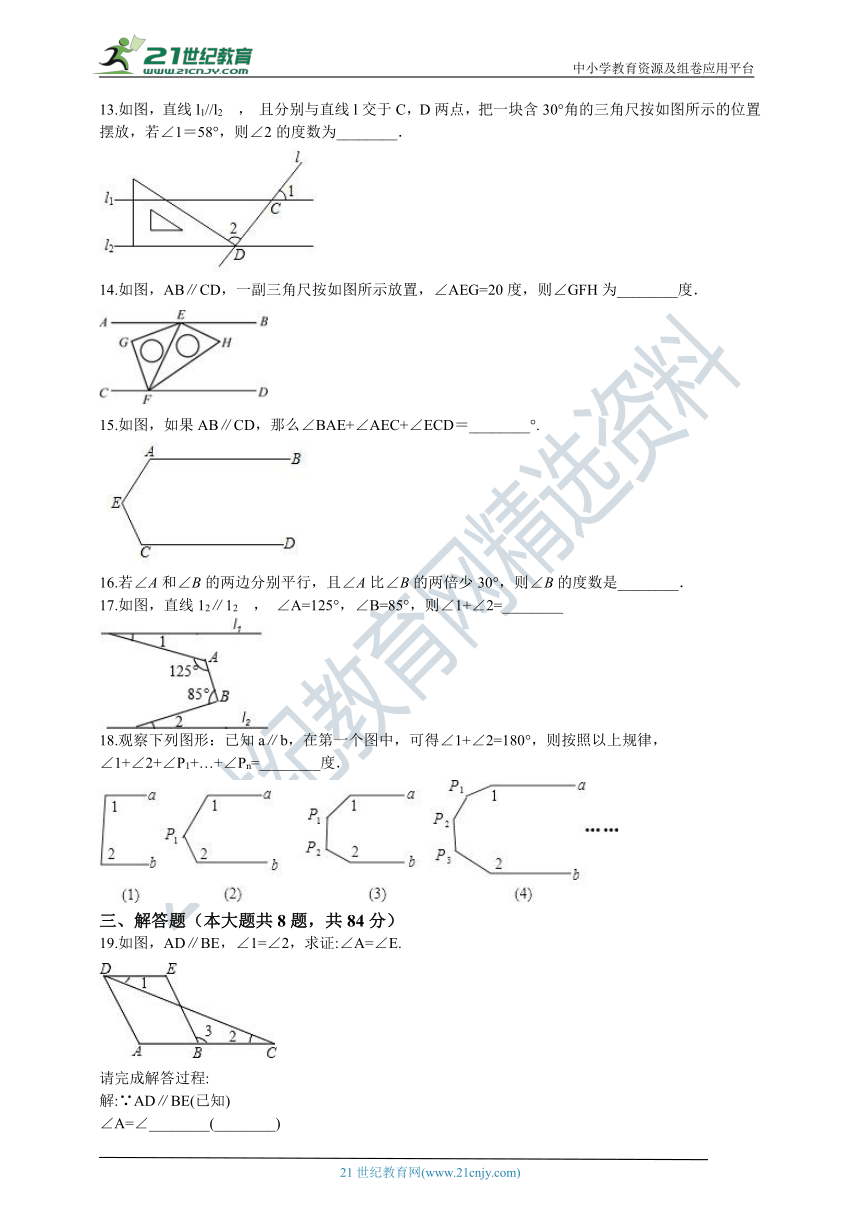
13.如图,直线l1//l2
,
且分别与直线l交于C,D两点,把一块含30°角的三角尺按如图所示的位置摆放,若∠1=58°,则∠2的度数为________.
14.如图,AB∥CD,一副三角尺按如图所示放置,∠AEG=20度,则∠GFH为________度.
15.如图,如果AB∥CD,那么∠BAE+∠AEC+∠ECD=________°.
16.若∠A和∠B的两边分别平行,且∠A比∠B的两倍少30°,则∠B的度数是________.
17.如图,直线12∥12
,
∠A=125°,∠B=85°,则∠1+∠2=________
18.观察下列图形:已知a∥b,在第一个图中,可得∠1+∠2=180°,则按照以上规律,∠1+∠2+∠P1+…+∠Pn=________度.
三、解答题(本大题共8题,共84分)
19.如图,AD∥BE,∠1=∠2,求证:∠A=∠E.
请完成解答过程:
解:∵AD∥BE(已知)
∠A=∠________(________)
又∵1=∠2(已知)
∴AC∥________(________)
∴∠3=∠________(两直线平行,内错角相等)
∴∠A=∠E(________)
20.如图,已知DE∥BC
,
CD是∠ACB的平分线,∠B=70°,∠ACB=50°,求∠EDC和∠AED的度数.
21.如图,已知:EF∥CD,∠1+∠2=180°,试判断∠BGD与∠BCA的大小,并给予证明.
22.如图,已知∠1=68°,∠2=50°,∠D=68°,AE∥BC.求:∠C的度数.
23.如图,AB∥CD,AB∥GE,∠B=110°,∠C=100°.∠BFC等于多少度?为什么?
24.如图,三角形
中,
.
分别在
延长线上,
,
.
(1)判断
和
的位置关系,并说明理由;
(2)求
的度数.
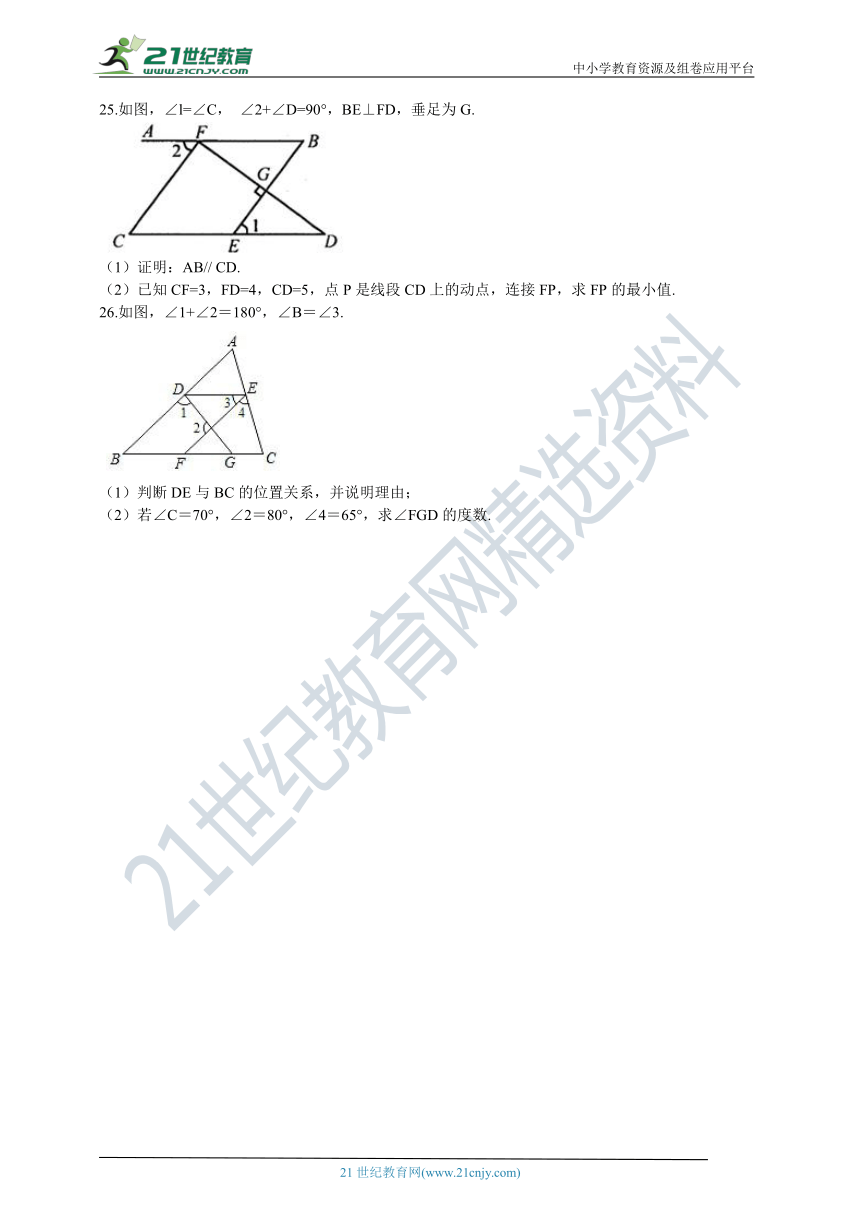
25.如图,∠l=∠C,
∠2+∠D=90°,BE⊥FD,垂足为G.
(1)证明:AB//
CD.
(2)已知CF=3,FD=4,CD=5,点P是线段CD上的动点,连接FP,求FP的最小值.
26.如图,∠1+∠2=180°,∠B=∠3.
(1)判断DE与BC的位置关系,并说明理由;
(2)若∠C=70°,∠2=80°,∠4=65°,求∠FGD的度数.
答案解析部分
一、单选题
1.【答案】
B
【考点】平行线的性质
解:如图,∵a∥b,
∴∠1=∠3=50°,
∴∠2=180°?50°=130°,
故答案为:B.
【分析】利用平行线的性质即可解决问题.
2.【答案】
B
【考点】平行线的判定与性质,对顶角及其性质
解:如图,
∵
,
∴a∥b,
∴∠4+∠5=180°,
∵∠5=
,
∴∠4=80°.
故答案为:B.
【分析】如图,由
可得a∥b,进而可得∠4+∠5=180°,由对顶角相等可得∠5=
,进一步即可求出结果.
3.【答案】
C
【考点】平行线的判定与性质
解:过点E作EF∥AB
,
∴∠B=∠BEF
,
∵AB∥CD
,
∴EF∥CD
,
∴∠D=∠FED
,
∴∠BED=∠BEF+∠DEF=∠B+∠D=23°+42°=65°.
故答案为:C.
【分析】过点E作EF∥AB
,
根据平行线的性质求解即可.
4.【答案】
C
【考点】平行线的判定与性质
解:直线a、b、c在同一平面内,(1)如果a⊥b,b⊥c,那么a∥c;正确.(2)如果a∥b,b∥c,c∥d,那么a∥d;正确.(3)如果a∥b,b⊥c,那么a⊥c;正确.(4)如果a与b相交,b与c相交,那么a与c相交.错误。所以正确的有3个,故选:C.
【分析】根据垂直于同一直线的两直线平行,平行公理对各小题分析判断即可得解.
5.【答案】
D
【考点】平行线的性质
解:∵两次拐弯后,按原来的相反方向前进,
∴两次拐弯的方向相同,形成的角是同位角,
故答案为:D.
【分析】根据平行线的性质分别判断得出即可.
6.【答案】
D
【考点】平行线的性质
解:作BD∥l1
,
如图所示:
∵BD∥l1
,
∴∠1=∠CBD,
双∵l1∥l2
,
∴BD∥l2
,
∴∠ABD=∠2,
又∵∠1=39°,
∴∠CDB=39°
又∵∠CBA=∠CBD+∠ABD=90°,
∴∠ABD=51°,
∴∠2=51°.
故答案为:D.
【分析】由BD∥l1得∠1=∠CBD=39°,根据平行公理的推论得BD∥l2
,
其性质得∠ABD=∠2,角的和差求得∠2=51°.
7.【答案】
B
【考点】平行线的性质
解:如下图,∵l1∥l4
,
∴∠1+∠4=180°,
又∵∠1=124°,
∴∠4=56°,
又∵∠2+∠4+∠3=180°,∠2=88°,
∴∠2=180°-56°-88°=36°.
故答案为:B.
【分析】如下图所示,根据“平行线的性质和平角的定义”进行分析解答即可.
8.【答案】
C
【考点】平行线的性质
解:过C作CF∥AB,
∵AB∥DE,
∴AB∥CF∥DE,
∴∠1=∠α=40°,∠2=180°-∠β,
∵∠BCD=90°,
∴∠1+∠2=40°+180°-∠β=90°,
∴∠β=130°.
故答案为:C.
【分析】过C作CF∥AB,根据平行线的性质得到∠1=∠α=40°,∠2=180°-∠β,于是得到结论.
9.【答案】
C
【考点】垂线,平行线的性质
解:∵∠ACB=90°,
∴∠ABC+∠CAB=90°.
∵CE⊥AB,
∴∠CAB+∠ACE=90°.
∵AB∥CD,
∴∠DCB=∠ABC,
∴∠DCB+∠CAB=90°.
∴与∠CAB互余的角有∠ACE,∠ABC,∠DCB,共3个,
故答案为:C.
【分析】先由∠ACB=90°可得出∠ABC+∠CAB=90°,然后由CE⊥AB可得出∠CAB+∠ACE=90°,再由平行线的性质可知∠DCB=∠ABC,故∠DCB+∠CAB=90°,由此可得出结论.
10.【答案】
C
【考点】平行线的性质
解:解:作直线EF//AB
∵AB//CD、EF//AB
∴AB//CD//EF
∴
?
+∠1=180°,
+∠2=180°
∵∠1+∠2=
∴
故答案为:C
【分析】本题考查平行线间的拐点问题,首先过拐点作平行线,再根据两直线平行,同旁内角互补即可得到答案.
二、填空题
11.【答案】
45°
【考点】平行线的性质
解:如图:
∵a∥b,
∴∠3=∠1=45°,
∴∠2=∠3=45°.
故答案为:45°.
【分析】要求∠2的度数,只需根据平行线的性质求得其对顶角的度数即可.
12.【答案】
60
【考点】角的平分线,平行线的性质
解:∵AB
CD,∠FGB=150°,
∴
,
∵FG
平分∠EFD,
∴
,
∵AB
CD,
∴
,
故答案为:60°.
【分析】根据两直线平行,同旁内角互补得到
,根据角平分线的定义可得
,再利用两直线平行,内错角相等即可求解.
13.【答案】
92°
【考点】平行线的性质
解:如图,
∵l1//l2
,
∴∠1=∠3=58°,
∵∠4=30°,
∴∠2=180°﹣∠3﹣∠4=180°﹣58°﹣30°=92°.
故答案为:92°.
【分析】根据两条直线平行,同位角相等可得∠1=∠3,再根据平角定义即可求出∠2的度数.
14.【答案】
35
【考点】平行线的判定与性质
解:过点G作AB平行线交EF于P,
∴∠EGP=∠AEG=20°,
∴∠PGF=70°,
∵AB//CD,
∴GP∥CD,
∴∠GFC=∠PGF=70°,
∴∠HFD=180°-∠GFC-∠GFP-∠EFH=35°.
故答案为:35.
【分析】过点G作AB平行线交EF于P,根据平行线的性质求出∠EGP,进而求出∠PGF,再根据平行线的性质、平角的概念计算即可.
15.【答案】
360
【考点】平行线的判定与性质
解:作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠BAE+∠AEF=180°,∠FEC+∠ECD=180°,
∵∠AEF+∠FEC=∠AEC,
∴∠BAE+∠AEC+∠ECD=360°,
故答案为:360.
【分析】作辅助线EF∥AB,然后根据平行线的性质,可以得到∠BAE+∠AEC+∠ECD的度数,本题得以解决.
16.【答案】
30°或70°
【考点】平行线的性质
解:∵∠A和∠B的两边分别平行,
∴∠A=∠B或∠A+∠B=180°,
∵∠A比∠B的两倍少30°,
即∠A=2∠B?30°,
∴2∠B?30°=∠B或2∠B?30°+∠B=180°,
∴∠B=30°或∠B=70°
故答案为:30°或70°.
【分析】由∠A和∠B的两边分别平行,即可得∠A=∠B或∠A+∠B=180°,又由∠A比∠B的两倍少30°,即可求得∠B的度数.
17.【答案】
30°
【考点】平行线的性质
解:如图,延长AB和BA,
∠1+∠3=125°,
∠2+∠4=85°,
∴∠1+∠2+∠3+∠4=210°,
=85°,
∵
12∥12
,
∴∠3+∠4=180°,
∴∠1+∠2=210°-180°=30°;
故答案为:30°.
【分析】延长AB与BA,分别有外角的性质得∠1和∠3,∠2和∠4度数之和,则∠1、∠2、∠3和∠4度数之和可求,再由两直线平行同旁内角互补得∠3和∠4度数之和,则∠1+∠2可求。
18.【答案】(n+1)×180
【考点】平行线的性质
解:如图,分别过P1、P2、P3作直线AB的平行线P1E,P2F,P3G,
∵AB∥CD,
∴AB∥P1E∥P2F∥P3G.
由平行线的性质可得出:∠1+∠3=180°,∠5+∠6=180°,∠7+∠8=180°,∠4+∠2=180°
∴(1)∠1+∠2=180°,(2)∠1+∠P1+∠2=2×180,(3)∠1+∠P1+∠P2+∠2=3×180°,(4)∠1+∠P1+∠P2+∠P3+∠2=4×180°,
∴∠1+∠2+∠P1+…+∠Pn=(n+1)×180°.
故答案为:(n+1)×180.
【分析】出现平行线间的折线可过折点作平行线构造出同旁内角,由同旁内角互补解决问题.
三、解答题
19.【答案】
3;两直线平行,同位角相等;DE;内错角相等,两直线平行;E;等量代换
【考点】平行线的判定与性质
分析:由于AD∥BE可以得到∠A=∠3,又∠1=∠2可以得到DE∥AC,由此可以证明∠E=∠3,等量代换即可证明题目结论.
20.【答案】
解:∵CD是∠ACB的平分线,∠ACB=50°,
∴∠DCB=∠ACD=25°,
又DE∥BC,
∴∠EDC=∠DCB=25°,
∠AED=∠ACB=50°.
【考点】平行线的性质
分析:根据角平分线的性质及平行线的性质即可求解.
21.【答案】
解:∠BGD=∠BCA,
证明如下:∵EF∥CD,
∴∠1+∠ECD=180°,
∵∠1+∠2=180°,
∴∠2=∠ECD,
∴AC∥DG,
∴∠BGD=∠BCA.
【考点】平行线的性质
分析:由EF∥CD可得到∠1+∠ECD=180°,结合条件可证明AC∥DG,再根据平行线的性质可得到∠BGD=∠BCA.
22.【答案】
解:∵∠1=∠D=68°,
∴AB∥CD,
∵∠2=50°,
∴∠AED=∠2=50°,
∵AE∥BC,
∴∠C=∠AED=50°
【考点】平行线的判定与性质
分析:由∠1=∠D
=68°,根据平行线的判定推出AB∥CD,又由AE∥BC,根据平行线的性质求出∠AED=∠2=50°,根据平行线的性质求出∠C=∠AED=50°即可.
23.【答案】
解:∠BFC等于30度,理由如下:
∵AB∥GE,
∴∠B+∠BFG=180°,
∵∠B=110°,
∴∠BFG=180°﹣110°=70°,
∵AB∥CD,AB∥GE,
∴CD∥GE,
∴∠C+∠CFE=180°,
∵∠C=100°.
∴∠CFE=180°﹣100°=80°,
∴∠BFC=180°﹣∠BFG﹣∠CFE=180°﹣70°﹣80°=30°.
【考点】平行线的性质
分析:由AB∥CD,AB∥GE得CD∥GE,根据两直线平行,同旁内角互补得到∠B+∠BFG=180°,∠C+∠CFE=180°,而∠B=110°,∠C=100°,可以求出∠BFG和∠CFE,最后可以求出∠BFC.
24.【答案】
(1)解:
.
理由如下:
,
(2)解:由(1)知,
,
∵
【考点】平行线的判定与性质
分析:(1)由题意知∠B=∠D,进而根据同位角二直线平行即可判断
;
(2)根据二直线平行,同旁内角互补即可算出∠BCE的度数.
25.【答案】
(1)证明:∵
,
∴CF∥BE,
∴
.
∵
,垂足为G,
∴
,
∴
.
∵
,
∴
,
∵
,
∴
,
∴
AB∥CD.
(2)解:根据题意,可知
的最小值是点F到直线CD的垂线段的长度.
过点F作
,垂足为P.
因为
,
所以
.
因为
,
,
,
所以
,所以
.
故FP的最小值为
.
【考点】垂线段最短,平行线的判定与性质
分析:(1)先证明CF∥BE,得到
,进而证明
,结合已知得到
即可证明AB∥CD;
(2)先确定
的最小值是点F到直线CD的垂线段的长度,过点F作
,垂足为P,再由等面积法即可计算出FP的值.
26.【答案】
(1)解:DE∥BC,理由如下:
∵∠1+∠2=180°,
∴AB∥EF,
∴∠ADE=∠3,
∵∠B=∠3,
∴∠ADE=∠B,
∴DE∥BC
(2)解:∵AB∥EF,
∴∠A=∠4=65°,
∵∠C=70°,
∴∠B=180°﹣∠A﹣∠C=45°,
∵∠1=180°﹣∠2=180°﹣80°=100°,
∴∠FGD=180°﹣∠1﹣∠B=180°﹣100°﹣45°=35°
答:∠FGD的度数为35°.
【考点】平行线的判定与性质
分析:(1)根据平行线的判定与性质即可判断DE与BC的位置关系;
(2)根据∠C=70°,∠2=80°,∠4=65°,及平行线的判定与性质即可求∠FGD的度数.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
初中数学苏科版七年级下册
7.2
探索平行线的性质
同步训练
一、单选题(本大题共10题,每题3分,共30分)
1.如图,已知直线
,
,则
的度数为(???
)
A.????????????????????????????????????B.????????????????????????????????????C.????????????????????????????????????D.?
2.如图,直线
与直线
相交,已知
,则
的度数是(?
)
A.???????????????????????????????????????B.???????????????????????????????????????C.???????????????????????????????????????D.?
3.直线AB∥CD
,
∠B=23°,∠D=42°,则∠E=(??
)
A.?23°???????????????????????????????????????B.?42°???????????????????????????????????????C.?65°???????????????????????????????????????D.?19°
4.直线a、b、c在同一平面内,(1)如果a⊥b,b⊥c,那么a∥c;(2)如果a∥b,b∥c,c∥d,那么a∥d;(3)如果a∥b,b⊥c,那么a⊥c;(4)如果a与b相交,b与c相交,那么a与c相交.在上述四种说法中,正确的个数为( )
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
5.一个学员在广场上驾驶汽车,两次拐弯后,行驶的方向与原来的方向相同,这两次拐弯的角度可能是(???
)
A.?第一次向右拐
50°
,第二次向左拐130°??????????????B.?第一次向右拐
50°
,第二次向右拐130°
C.?第一次向左拐
50°
,第二次向左拐130°??????????????D.?第一次向左拐
30°
,第二次向右拐
30°
6.如图,已知直线l1∥l2
,
将一块直角三角板ABC按如图所示方式放置,若∠1=39°,则∠2等于(??
)
A.?39°???????????????????????????????????????B.?45°???????????????????????????????????????C.?50°???????????????????????????????????????D.?51°
7.如图,直线
,
,
交于一点,直线
,若
,
,则
的度数为
???
A.????????????????????????????????????????B.????????????????????????????????????????C.????????????????????????????????????????D.?
8.如图,∠BCD=90°,AB∥DE
,
若∠α=40°,则∠β的大小为(?
)
A.?150°????????????????????????????????????B.?140°????????????????????????????????????C.?130°????????????????????????????????????D.?120°
9.如图,
,
,
,垂足为
,图中与
互余的角有(?
)
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
10.如图,已知AB//CD,则
,
,
之间的等量关系为(??
)
A.??????????????????????????????????B.?
C.??????????????????????????????????D.?
二、填空题(本大题共8题,每题2分,共16分)
11.如图所示,直线a∥b,如果∠1=45°,那么∠2的度数是________.
12.如图,AB∥CD,∠FGB=150°,FG
平分∠EFD,则∠AEF
的度数于________°.
13.如图,直线l1//l2
,
且分别与直线l交于C,D两点,把一块含30°角的三角尺按如图所示的位置摆放,若∠1=58°,则∠2的度数为________.
14.如图,AB∥CD,一副三角尺按如图所示放置,∠AEG=20度,则∠GFH为________度.
15.如图,如果AB∥CD,那么∠BAE+∠AEC+∠ECD=________°.
16.若∠A和∠B的两边分别平行,且∠A比∠B的两倍少30°,则∠B的度数是________.
17.如图,直线12∥12
,
∠A=125°,∠B=85°,则∠1+∠2=________
18.观察下列图形:已知a∥b,在第一个图中,可得∠1+∠2=180°,则按照以上规律,∠1+∠2+∠P1+…+∠Pn=________度.
三、解答题(本大题共8题,共84分)
19.如图,AD∥BE,∠1=∠2,求证:∠A=∠E.
请完成解答过程:
解:∵AD∥BE(已知)
∠A=∠________(________)
又∵1=∠2(已知)
∴AC∥________(________)
∴∠3=∠________(两直线平行,内错角相等)
∴∠A=∠E(________)
20.如图,已知DE∥BC
,
CD是∠ACB的平分线,∠B=70°,∠ACB=50°,求∠EDC和∠AED的度数.
21.如图,已知:EF∥CD,∠1+∠2=180°,试判断∠BGD与∠BCA的大小,并给予证明.
22.如图,已知∠1=68°,∠2=50°,∠D=68°,AE∥BC.求:∠C的度数.
23.如图,AB∥CD,AB∥GE,∠B=110°,∠C=100°.∠BFC等于多少度?为什么?
24.如图,三角形
中,
.
分别在
延长线上,
,
.
(1)判断
和
的位置关系,并说明理由;
(2)求
的度数.
25.如图,∠l=∠C,
∠2+∠D=90°,BE⊥FD,垂足为G.
(1)证明:AB//
CD.
(2)已知CF=3,FD=4,CD=5,点P是线段CD上的动点,连接FP,求FP的最小值.
26.如图,∠1+∠2=180°,∠B=∠3.
(1)判断DE与BC的位置关系,并说明理由;
(2)若∠C=70°,∠2=80°,∠4=65°,求∠FGD的度数.
答案解析部分
一、单选题
1.【答案】
B
【考点】平行线的性质
解:如图,∵a∥b,
∴∠1=∠3=50°,
∴∠2=180°?50°=130°,
故答案为:B.
【分析】利用平行线的性质即可解决问题.
2.【答案】
B
【考点】平行线的判定与性质,对顶角及其性质
解:如图,
∵
,
∴a∥b,
∴∠4+∠5=180°,
∵∠5=
,
∴∠4=80°.
故答案为:B.
【分析】如图,由
可得a∥b,进而可得∠4+∠5=180°,由对顶角相等可得∠5=
,进一步即可求出结果.
3.【答案】
C
【考点】平行线的判定与性质
解:过点E作EF∥AB
,
∴∠B=∠BEF
,
∵AB∥CD
,
∴EF∥CD
,
∴∠D=∠FED
,
∴∠BED=∠BEF+∠DEF=∠B+∠D=23°+42°=65°.
故答案为:C.
【分析】过点E作EF∥AB
,
根据平行线的性质求解即可.
4.【答案】
C
【考点】平行线的判定与性质
解:直线a、b、c在同一平面内,(1)如果a⊥b,b⊥c,那么a∥c;正确.(2)如果a∥b,b∥c,c∥d,那么a∥d;正确.(3)如果a∥b,b⊥c,那么a⊥c;正确.(4)如果a与b相交,b与c相交,那么a与c相交.错误。所以正确的有3个,故选:C.
【分析】根据垂直于同一直线的两直线平行,平行公理对各小题分析判断即可得解.
5.【答案】
D
【考点】平行线的性质
解:∵两次拐弯后,按原来的相反方向前进,
∴两次拐弯的方向相同,形成的角是同位角,
故答案为:D.
【分析】根据平行线的性质分别判断得出即可.
6.【答案】
D
【考点】平行线的性质
解:作BD∥l1
,
如图所示:
∵BD∥l1
,
∴∠1=∠CBD,
双∵l1∥l2
,
∴BD∥l2
,
∴∠ABD=∠2,
又∵∠1=39°,
∴∠CDB=39°
又∵∠CBA=∠CBD+∠ABD=90°,
∴∠ABD=51°,
∴∠2=51°.
故答案为:D.
【分析】由BD∥l1得∠1=∠CBD=39°,根据平行公理的推论得BD∥l2
,
其性质得∠ABD=∠2,角的和差求得∠2=51°.
7.【答案】
B
【考点】平行线的性质
解:如下图,∵l1∥l4
,
∴∠1+∠4=180°,
又∵∠1=124°,
∴∠4=56°,
又∵∠2+∠4+∠3=180°,∠2=88°,
∴∠2=180°-56°-88°=36°.
故答案为:B.
【分析】如下图所示,根据“平行线的性质和平角的定义”进行分析解答即可.
8.【答案】
C
【考点】平行线的性质
解:过C作CF∥AB,
∵AB∥DE,
∴AB∥CF∥DE,
∴∠1=∠α=40°,∠2=180°-∠β,
∵∠BCD=90°,
∴∠1+∠2=40°+180°-∠β=90°,
∴∠β=130°.
故答案为:C.
【分析】过C作CF∥AB,根据平行线的性质得到∠1=∠α=40°,∠2=180°-∠β,于是得到结论.
9.【答案】
C
【考点】垂线,平行线的性质
解:∵∠ACB=90°,
∴∠ABC+∠CAB=90°.
∵CE⊥AB,
∴∠CAB+∠ACE=90°.
∵AB∥CD,
∴∠DCB=∠ABC,
∴∠DCB+∠CAB=90°.
∴与∠CAB互余的角有∠ACE,∠ABC,∠DCB,共3个,
故答案为:C.
【分析】先由∠ACB=90°可得出∠ABC+∠CAB=90°,然后由CE⊥AB可得出∠CAB+∠ACE=90°,再由平行线的性质可知∠DCB=∠ABC,故∠DCB+∠CAB=90°,由此可得出结论.
10.【答案】
C
【考点】平行线的性质
解:解:作直线EF//AB
∵AB//CD、EF//AB
∴AB//CD//EF
∴
?
+∠1=180°,
+∠2=180°
∵∠1+∠2=
∴
故答案为:C
【分析】本题考查平行线间的拐点问题,首先过拐点作平行线,再根据两直线平行,同旁内角互补即可得到答案.
二、填空题
11.【答案】
45°
【考点】平行线的性质
解:如图:
∵a∥b,
∴∠3=∠1=45°,
∴∠2=∠3=45°.
故答案为:45°.
【分析】要求∠2的度数,只需根据平行线的性质求得其对顶角的度数即可.
12.【答案】
60
【考点】角的平分线,平行线的性质
解:∵AB
CD,∠FGB=150°,
∴
,
∵FG
平分∠EFD,
∴
,
∵AB
CD,
∴
,
故答案为:60°.
【分析】根据两直线平行,同旁内角互补得到
,根据角平分线的定义可得
,再利用两直线平行,内错角相等即可求解.
13.【答案】
92°
【考点】平行线的性质
解:如图,
∵l1//l2
,
∴∠1=∠3=58°,
∵∠4=30°,
∴∠2=180°﹣∠3﹣∠4=180°﹣58°﹣30°=92°.
故答案为:92°.
【分析】根据两条直线平行,同位角相等可得∠1=∠3,再根据平角定义即可求出∠2的度数.
14.【答案】
35
【考点】平行线的判定与性质
解:过点G作AB平行线交EF于P,
∴∠EGP=∠AEG=20°,
∴∠PGF=70°,
∵AB//CD,
∴GP∥CD,
∴∠GFC=∠PGF=70°,
∴∠HFD=180°-∠GFC-∠GFP-∠EFH=35°.
故答案为:35.
【分析】过点G作AB平行线交EF于P,根据平行线的性质求出∠EGP,进而求出∠PGF,再根据平行线的性质、平角的概念计算即可.
15.【答案】
360
【考点】平行线的判定与性质
解:作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠BAE+∠AEF=180°,∠FEC+∠ECD=180°,
∵∠AEF+∠FEC=∠AEC,
∴∠BAE+∠AEC+∠ECD=360°,
故答案为:360.
【分析】作辅助线EF∥AB,然后根据平行线的性质,可以得到∠BAE+∠AEC+∠ECD的度数,本题得以解决.
16.【答案】
30°或70°
【考点】平行线的性质
解:∵∠A和∠B的两边分别平行,
∴∠A=∠B或∠A+∠B=180°,
∵∠A比∠B的两倍少30°,
即∠A=2∠B?30°,
∴2∠B?30°=∠B或2∠B?30°+∠B=180°,
∴∠B=30°或∠B=70°
故答案为:30°或70°.
【分析】由∠A和∠B的两边分别平行,即可得∠A=∠B或∠A+∠B=180°,又由∠A比∠B的两倍少30°,即可求得∠B的度数.
17.【答案】
30°
【考点】平行线的性质
解:如图,延长AB和BA,
∠1+∠3=125°,
∠2+∠4=85°,
∴∠1+∠2+∠3+∠4=210°,
=85°,
∵
12∥12
,
∴∠3+∠4=180°,
∴∠1+∠2=210°-180°=30°;
故答案为:30°.
【分析】延长AB与BA,分别有外角的性质得∠1和∠3,∠2和∠4度数之和,则∠1、∠2、∠3和∠4度数之和可求,再由两直线平行同旁内角互补得∠3和∠4度数之和,则∠1+∠2可求。
18.【答案】(n+1)×180
【考点】平行线的性质
解:如图,分别过P1、P2、P3作直线AB的平行线P1E,P2F,P3G,
∵AB∥CD,
∴AB∥P1E∥P2F∥P3G.
由平行线的性质可得出:∠1+∠3=180°,∠5+∠6=180°,∠7+∠8=180°,∠4+∠2=180°
∴(1)∠1+∠2=180°,(2)∠1+∠P1+∠2=2×180,(3)∠1+∠P1+∠P2+∠2=3×180°,(4)∠1+∠P1+∠P2+∠P3+∠2=4×180°,
∴∠1+∠2+∠P1+…+∠Pn=(n+1)×180°.
故答案为:(n+1)×180.
【分析】出现平行线间的折线可过折点作平行线构造出同旁内角,由同旁内角互补解决问题.
三、解答题
19.【答案】
3;两直线平行,同位角相等;DE;内错角相等,两直线平行;E;等量代换
【考点】平行线的判定与性质
分析:由于AD∥BE可以得到∠A=∠3,又∠1=∠2可以得到DE∥AC,由此可以证明∠E=∠3,等量代换即可证明题目结论.
20.【答案】
解:∵CD是∠ACB的平分线,∠ACB=50°,
∴∠DCB=∠ACD=25°,
又DE∥BC,
∴∠EDC=∠DCB=25°,
∠AED=∠ACB=50°.
【考点】平行线的性质
分析:根据角平分线的性质及平行线的性质即可求解.
21.【答案】
解:∠BGD=∠BCA,
证明如下:∵EF∥CD,
∴∠1+∠ECD=180°,
∵∠1+∠2=180°,
∴∠2=∠ECD,
∴AC∥DG,
∴∠BGD=∠BCA.
【考点】平行线的性质
分析:由EF∥CD可得到∠1+∠ECD=180°,结合条件可证明AC∥DG,再根据平行线的性质可得到∠BGD=∠BCA.
22.【答案】
解:∵∠1=∠D=68°,
∴AB∥CD,
∵∠2=50°,
∴∠AED=∠2=50°,
∵AE∥BC,
∴∠C=∠AED=50°
【考点】平行线的判定与性质
分析:由∠1=∠D
=68°,根据平行线的判定推出AB∥CD,又由AE∥BC,根据平行线的性质求出∠AED=∠2=50°,根据平行线的性质求出∠C=∠AED=50°即可.
23.【答案】
解:∠BFC等于30度,理由如下:
∵AB∥GE,
∴∠B+∠BFG=180°,
∵∠B=110°,
∴∠BFG=180°﹣110°=70°,
∵AB∥CD,AB∥GE,
∴CD∥GE,
∴∠C+∠CFE=180°,
∵∠C=100°.
∴∠CFE=180°﹣100°=80°,
∴∠BFC=180°﹣∠BFG﹣∠CFE=180°﹣70°﹣80°=30°.
【考点】平行线的性质
分析:由AB∥CD,AB∥GE得CD∥GE,根据两直线平行,同旁内角互补得到∠B+∠BFG=180°,∠C+∠CFE=180°,而∠B=110°,∠C=100°,可以求出∠BFG和∠CFE,最后可以求出∠BFC.
24.【答案】
(1)解:
.
理由如下:
,
(2)解:由(1)知,
,
∵
【考点】平行线的判定与性质
分析:(1)由题意知∠B=∠D,进而根据同位角二直线平行即可判断
;
(2)根据二直线平行,同旁内角互补即可算出∠BCE的度数.
25.【答案】
(1)证明:∵
,
∴CF∥BE,
∴
.
∵
,垂足为G,
∴
,
∴
.
∵
,
∴
,
∵
,
∴
,
∴
AB∥CD.
(2)解:根据题意,可知
的最小值是点F到直线CD的垂线段的长度.
过点F作
,垂足为P.
因为
,
所以
.
因为
,
,
,
所以
,所以
.
故FP的最小值为
.
【考点】垂线段最短,平行线的判定与性质
分析:(1)先证明CF∥BE,得到
,进而证明
,结合已知得到
即可证明AB∥CD;
(2)先确定
的最小值是点F到直线CD的垂线段的长度,过点F作
,垂足为P,再由等面积法即可计算出FP的值.
26.【答案】
(1)解:DE∥BC,理由如下:
∵∠1+∠2=180°,
∴AB∥EF,
∴∠ADE=∠3,
∵∠B=∠3,
∴∠ADE=∠B,
∴DE∥BC
(2)解:∵AB∥EF,
∴∠A=∠4=65°,
∵∠C=70°,
∴∠B=180°﹣∠A﹣∠C=45°,
∵∠1=180°﹣∠2=180°﹣80°=100°,
∴∠FGD=180°﹣∠1﹣∠B=180°﹣100°﹣45°=35°
答:∠FGD的度数为35°.
【考点】平行线的判定与性质
分析:(1)根据平行线的判定与性质即可判断DE与BC的位置关系;
(2)根据∠C=70°,∠2=80°,∠4=65°,及平行线的判定与性质即可求∠FGD的度数.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
