2.2.1用样本的频率分布估计总体分布(2)
文档属性
| 名称 | 2.2.1用样本的频率分布估计总体分布(2) |  | |
| 格式 | rar | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-01 16:41:21 | ||
图片预览



文档简介
(共12张PPT)
(2)
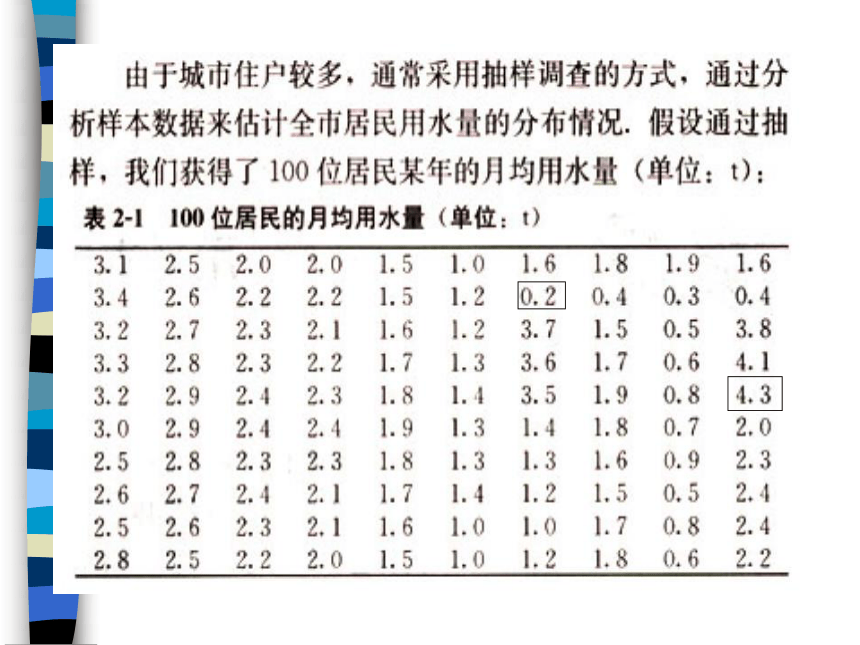
1、求极差(即一组数据中最大值与最小值的差)
知道这组数据的变动范围4.3-0.2=4.1
2、决定组距与组数(将数据分组)
3、 将数据分组(8.2取整,分为9组)
复习:画频率分布直方图的步骤
4、列出频率分布表.(学生填写频率/组距一栏)
5、画出频率分布直方图。
组距:指每个小组的两个端点的距离,组距
组数:将数据分组,当数据在100个以内时,
按数据多少常分5-12组。
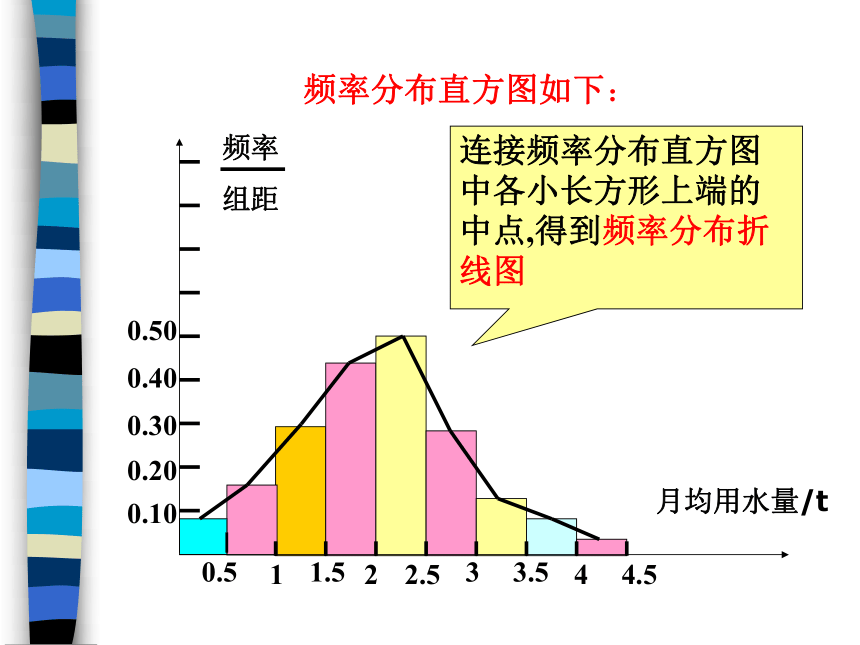
频率分布直方图如下:
月均用水量/t
频率
组距
0.10
0.20
0.30
0.40
0.50
0.5
1
1.5
2
2.5
3
3.5
4
4.5
连接频率分布直方图中各小长方形上端的中点,得到频率分布折线图
利用样本频分布对总体分布进行相应估计
(3)当样本容量无限增大,组距无限缩小,那么频率分布直方图就会无限接近于一条光滑曲线——总体密度曲线。
(2)样本容量越大,这种估计越精确。
(1)上例的样本容量为100,如果增至1000,其频率分布直方图的情况会有什么变化?假如增至10000呢?
总体密度曲线
频率
组距
月均用水量/t
a
b
(图中阴影部分的面积,表示总体在某个区间 (a, b) 内取值的百分比)。
用样本分布直方图去估计相应的总体分布时,一般样本容量越大,频率分布直方图就会无限接近总体密度曲线,就越精确地反映了总体的分布规律,即越精确地反映了总体在各个范围内取值百分比。
总体密度曲线反映了总体在各个范围内取值的百分比,精确地反映了总体的分布规律。是研究总体分布的工具.
总体密度曲线
茎叶图
某赛季甲、乙两名篮球运动员每场比赛得分的原始记录如下:
(1)甲运动员得分:
13,51,23,8,26,38,16,33,14,28,39
(1)乙运动员得分: 49,24,12,31,50,31,44,36,15,37,25,36,39
茎叶图
甲
乙
0
1
2
3
4
5
2 5
5 4
1 6 1 6 7 9
4 9
0
8
4 6 3
6 8
3 8 9
1
某篮球学校的甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个.得分情况用右面的茎叶图表示(中间的数表示两位运动员得分的十位数,两边的数字分别表示两人得分的个位数字).则甲得分的中位数是________;乙得分的平均数是_______。
在某中学举行的数学知识竞赛中,将所有参赛学生的成绩进行整理后分成5组:[50,60),[60,70),[70,80),[80,90),[90,100),绘制出如图所示的频率分布直方图。已知成绩在[70,80)的频数是15。
(1)求成绩在[50,70)分的频率;
(2)求参赛学生的总人数;
(3)求成绩在[80,100)分的学生人数;
(2)
1、求极差(即一组数据中最大值与最小值的差)
知道这组数据的变动范围4.3-0.2=4.1
2、决定组距与组数(将数据分组)
3、 将数据分组(8.2取整,分为9组)
复习:画频率分布直方图的步骤
4、列出频率分布表.(学生填写频率/组距一栏)
5、画出频率分布直方图。
组距:指每个小组的两个端点的距离,组距
组数:将数据分组,当数据在100个以内时,
按数据多少常分5-12组。
频率分布直方图如下:
月均用水量/t
频率
组距
0.10
0.20
0.30
0.40
0.50
0.5
1
1.5
2
2.5
3
3.5
4
4.5
连接频率分布直方图中各小长方形上端的中点,得到频率分布折线图
利用样本频分布对总体分布进行相应估计
(3)当样本容量无限增大,组距无限缩小,那么频率分布直方图就会无限接近于一条光滑曲线——总体密度曲线。
(2)样本容量越大,这种估计越精确。
(1)上例的样本容量为100,如果增至1000,其频率分布直方图的情况会有什么变化?假如增至10000呢?
总体密度曲线
频率
组距
月均用水量/t
a
b
(图中阴影部分的面积,表示总体在某个区间 (a, b) 内取值的百分比)。
用样本分布直方图去估计相应的总体分布时,一般样本容量越大,频率分布直方图就会无限接近总体密度曲线,就越精确地反映了总体的分布规律,即越精确地反映了总体在各个范围内取值百分比。
总体密度曲线反映了总体在各个范围内取值的百分比,精确地反映了总体的分布规律。是研究总体分布的工具.
总体密度曲线
茎叶图
某赛季甲、乙两名篮球运动员每场比赛得分的原始记录如下:
(1)甲运动员得分:
13,51,23,8,26,38,16,33,14,28,39
(1)乙运动员得分: 49,24,12,31,50,31,44,36,15,37,25,36,39
茎叶图
甲
乙
0
1
2
3
4
5
2 5
5 4
1 6 1 6 7 9
4 9
0
8
4 6 3
6 8
3 8 9
1
某篮球学校的甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个.得分情况用右面的茎叶图表示(中间的数表示两位运动员得分的十位数,两边的数字分别表示两人得分的个位数字).则甲得分的中位数是________;乙得分的平均数是_______。
在某中学举行的数学知识竞赛中,将所有参赛学生的成绩进行整理后分成5组:[50,60),[60,70),[70,80),[80,90),[90,100),绘制出如图所示的频率分布直方图。已知成绩在[70,80)的频数是15。
(1)求成绩在[50,70)分的频率;
(2)求参赛学生的总人数;
(3)求成绩在[80,100)分的学生人数;
