用样本估计总体
图片预览

文档简介
用样本估计总体
【知识点总结】
1.频率分布直方图
(1)通常我们对总体作出的估计一般分成两种, 一种是用 .另一种 是用 .
(2)在频率分布直方图中,纵轴表示 ,数据 落在各小组内的频率用 表示. 各小长方形的面积总和
(3)连结频率分布直方图中各小长方形上端的中 点,就得到频率分布折线图.随着 的增加,作图时所分的 增加,相应的频率分布折线图就会越来越接近于一条光滑的曲线,统计中 称之为 ,它能够更加精细的反映出 .
(4)当样本数据较少时,用茎叶图表示数据的效果较好,它不但可以 ,而且可以 ,给数据的 和 都带来方便.
2.用样本的数字特征估计总体的数字特征
(1)众数、中位数、平均数
众数:在一组数据中,出现次数 的数据叫做这组数据的众数.
中位数:将一组数据按大小依次排列,把处在 位置的一个数据(或最中间两个数据的平均数)叫做这组数据的 .
平均数:样本数据的算术平均数.即 = .
在频率分布直方图中,中位数左边和右边的直方图的面积应该 .
(2)样本方差、标准差
标准差s= 其中是 ,n是 ____________________, 是_______________ 是反映总体波动大小的特征数,样本方差是标准差的 .通常用样本方差估计总体方差,当 时,样本方差很接近总体方差.
3、标准差、方差
1.标准差
考察样本数据的分散程度的大小,最常用的统计量是标准差。标准差是样本数据到平均数的一种平均距离,一般用s表示。
样本数据的标准差的算法:
、算出样本数据的平均数。
、算出每个样本数据与样本数据平均数的差:
、算出(2)中的平方。
、算出(3)中n个平方数的平均数,即为样本方差。
、算出(4)中平均数的算术平方根,,即为样本标准差。
其计算公式为:
显然,标准差较大,数据的离散程度较大;标准差较小,数据的离散程度较小。
2.方差
【例题精析】
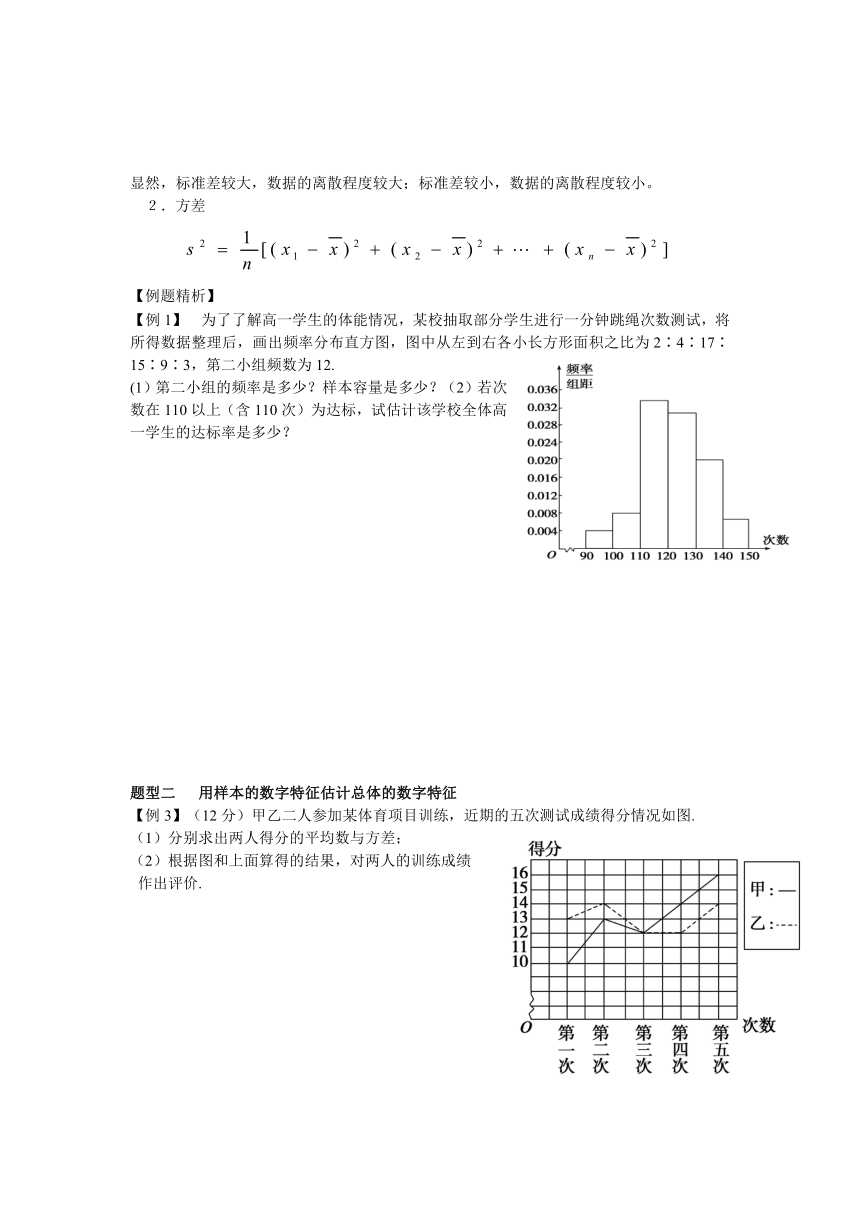
【例1】 为了了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图,图中从左到右各小长方形面积之比为2∶4∶17∶15∶9∶3,第二小组频数为12.
(1)第二小组的频率是多少?样本容量是多少?(2)若次数在110以上(含110次)为达标,试估计该学校全体高一学生的达标率是多少?
题型二 用样本的数字特征估计总体的数字特征
【例3】(12分)甲乙二人参加某体育项目训练,近期的五次测试成绩得分情况如图.
(1)分别求出两人得分的平均数与方差;
(2)根据图和上面算得的结果,对两人的训练成绩
作出评价.
【随堂练习】
一、选择题
1. 在频率分布直方图中,小矩形的高表示( )
A.频率/样本容量 B.组距×频率 C.频率 D.频率/组距
2. 在用样本频率估计总体分布的过程中,下列说法中正确的是( )
A.总体容量越大,估计越精确 B.总体容量越小,估计越精确
C.样本容量越大,估计越精确 D.样本容量越小,估计越精确
3. 一个容量为20的样本数据,分组后组距与频数如下表:
组距 [10,20) [20,30) [30,40) [40,50) [50,60) [60,70)
频数 2 3 4 5 4 2
则样本在区间(-∞,50)上的频率为( )
A.0.5 B.0.25 C.0.6 D.0.7
4. 10个小球分别编有号码1,2,3,4,其中1号球4个,2号球2个,3号球3个,4号球1个,数0.4是指1号球占总体分布的( )
A.频数 B.频率 C.频率/组距 D.累计频率
5. 已知样本:12,7,11,12,11,12,10,10,9,8,13,12,10,9,6,11,8,9,8,10,那么频率为0.25的样本的范围是( )
A.[5.5,7.5) B.[7.5,9.5) C.[9.5,11.5) D.[11.5,13.5)
6. 在统计中,样本的标准差可以近似地反映总体的( )
A.平均状态 B.分布规律 C.波动大小 D.最大值和最小值
7. 频率分布直方图的重心是( )
A.众数 B.中位数 C.标准差 D.平均数
8. 能反映一组数据的离散程度的是( )
A.众数 B.平均数 C.标准差 D.极差
9. 与原数据单位不一样的是( )
A.众数 B.平均数 C.标准差 D.方差
10.下列数字特征一定是数据组中数据的是( )
A.众数 B.中位数 C.标准差 D.平均数
11. 频率分布直方图中最高小矩形的中间位置所对的数字特征是( )
A.中位数 B.众数 C.平均数 D.标准差
12. 甲、乙两支女子曲棍球队在去年的国际联赛中,甲队平均每场进球数为3.2,全年比赛进球个数的标准差为3;乙队平均每场进球数为1.8,全年比赛进球个数的标准差为0.3.下列说法正确的个数为( )
①甲队的技术比乙队好 ②乙队发挥比甲队稳定 ③乙队几乎每场都进球 ④甲队的表现时好时坏
A.1 B.2 C.3 D.4
13.频率分布直方图的重心是( ).
A.平均数 B.众数 C.中位数 D.标准差
14.下列说法错误的是( ).
A.在统计里,把所需考察对象的全体叫作总体
B.一组数据的平均数一定大于这组数据中的每个数据
C.平均数、众数与中位数从不同的角度描述了一组数据的集中趋势
D.一组数据的方差越大,说明这组数据的波动越大
15.数据的方差为,则数据的方差为( ).
A. B. C. D.
二、填空题
16.一个容量为n的样本分成若干组,已知某组的频数和频率分别是30和0.25,则n=________.
17. 从某校2100名学生随机抽取一个30名学生的样本,样本中每个学生用于课外作业的时间(单位:min)依次为:75,80,85,65,95,100,70,55,65,75, 85,110,120,80,85,80,75,90,90,95,70,60,60,75,90,95,65,75,80,80.该校的学生中作业时间超过一个半小时(含一个半小时)的学生有____________人.
18. 频率分布直方图中各小长方体的面积和为____________.
19. 数据-2,-1,0,1,2的方差是____________.
20. 五个数1,2,3,4,a的平均数是3,则a=____,这五个数的标准差是_________.
21. 已知一个样本方差为,则这个样本的容量是____________,平均数是____________.
三、解答题
22.对某电子元件进行寿命追踪调查,情况如下:
寿命(h) 100~200 200~300 300~400 400~500 500~600
个 数 20 30 80 40 30
(1)列出频率分布表; (2)画出频率分布直方图;
(3)估计元件寿命在100~400 h以内的在总体中占的比例;
(4)估计电子元件寿命在400 h以上的在总体中占的比例.
23. 对甲、乙两名自行车赛手在相同条件下进行了6次测试,测得他们的最大速度(m/s)的数据如下表.
甲 27 38 30 37 35 31
乙 33 29 38 34 28 36
(1)画出茎叶图,由茎叶图你能获得哪些信息?
(2)分别求出甲、乙两名自行车赛手最大速度(m/s)数据的平均数、中位数、标准差,并判断选谁参加比赛更合适.
【知识点总结】
1.频率分布直方图
(1)通常我们对总体作出的估计一般分成两种, 一种是用 .另一种 是用 .
(2)在频率分布直方图中,纵轴表示 ,数据 落在各小组内的频率用 表示. 各小长方形的面积总和
(3)连结频率分布直方图中各小长方形上端的中 点,就得到频率分布折线图.随着 的增加,作图时所分的 增加,相应的频率分布折线图就会越来越接近于一条光滑的曲线,统计中 称之为 ,它能够更加精细的反映出 .
(4)当样本数据较少时,用茎叶图表示数据的效果较好,它不但可以 ,而且可以 ,给数据的 和 都带来方便.
2.用样本的数字特征估计总体的数字特征
(1)众数、中位数、平均数
众数:在一组数据中,出现次数 的数据叫做这组数据的众数.
中位数:将一组数据按大小依次排列,把处在 位置的一个数据(或最中间两个数据的平均数)叫做这组数据的 .
平均数:样本数据的算术平均数.即 = .
在频率分布直方图中,中位数左边和右边的直方图的面积应该 .
(2)样本方差、标准差
标准差s= 其中是 ,n是 ____________________, 是_______________ 是反映总体波动大小的特征数,样本方差是标准差的 .通常用样本方差估计总体方差,当 时,样本方差很接近总体方差.
3、标准差、方差
1.标准差
考察样本数据的分散程度的大小,最常用的统计量是标准差。标准差是样本数据到平均数的一种平均距离,一般用s表示。
样本数据的标准差的算法:
、算出样本数据的平均数。
、算出每个样本数据与样本数据平均数的差:
、算出(2)中的平方。
、算出(3)中n个平方数的平均数,即为样本方差。
、算出(4)中平均数的算术平方根,,即为样本标准差。
其计算公式为:
显然,标准差较大,数据的离散程度较大;标准差较小,数据的离散程度较小。
2.方差
【例题精析】
【例1】 为了了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图,图中从左到右各小长方形面积之比为2∶4∶17∶15∶9∶3,第二小组频数为12.
(1)第二小组的频率是多少?样本容量是多少?(2)若次数在110以上(含110次)为达标,试估计该学校全体高一学生的达标率是多少?
题型二 用样本的数字特征估计总体的数字特征
【例3】(12分)甲乙二人参加某体育项目训练,近期的五次测试成绩得分情况如图.
(1)分别求出两人得分的平均数与方差;
(2)根据图和上面算得的结果,对两人的训练成绩
作出评价.
【随堂练习】
一、选择题
1. 在频率分布直方图中,小矩形的高表示( )
A.频率/样本容量 B.组距×频率 C.频率 D.频率/组距
2. 在用样本频率估计总体分布的过程中,下列说法中正确的是( )
A.总体容量越大,估计越精确 B.总体容量越小,估计越精确
C.样本容量越大,估计越精确 D.样本容量越小,估计越精确
3. 一个容量为20的样本数据,分组后组距与频数如下表:
组距 [10,20) [20,30) [30,40) [40,50) [50,60) [60,70)
频数 2 3 4 5 4 2
则样本在区间(-∞,50)上的频率为( )
A.0.5 B.0.25 C.0.6 D.0.7
4. 10个小球分别编有号码1,2,3,4,其中1号球4个,2号球2个,3号球3个,4号球1个,数0.4是指1号球占总体分布的( )
A.频数 B.频率 C.频率/组距 D.累计频率
5. 已知样本:12,7,11,12,11,12,10,10,9,8,13,12,10,9,6,11,8,9,8,10,那么频率为0.25的样本的范围是( )
A.[5.5,7.5) B.[7.5,9.5) C.[9.5,11.5) D.[11.5,13.5)
6. 在统计中,样本的标准差可以近似地反映总体的( )
A.平均状态 B.分布规律 C.波动大小 D.最大值和最小值
7. 频率分布直方图的重心是( )
A.众数 B.中位数 C.标准差 D.平均数
8. 能反映一组数据的离散程度的是( )
A.众数 B.平均数 C.标准差 D.极差
9. 与原数据单位不一样的是( )
A.众数 B.平均数 C.标准差 D.方差
10.下列数字特征一定是数据组中数据的是( )
A.众数 B.中位数 C.标准差 D.平均数
11. 频率分布直方图中最高小矩形的中间位置所对的数字特征是( )
A.中位数 B.众数 C.平均数 D.标准差
12. 甲、乙两支女子曲棍球队在去年的国际联赛中,甲队平均每场进球数为3.2,全年比赛进球个数的标准差为3;乙队平均每场进球数为1.8,全年比赛进球个数的标准差为0.3.下列说法正确的个数为( )
①甲队的技术比乙队好 ②乙队发挥比甲队稳定 ③乙队几乎每场都进球 ④甲队的表现时好时坏
A.1 B.2 C.3 D.4
13.频率分布直方图的重心是( ).
A.平均数 B.众数 C.中位数 D.标准差
14.下列说法错误的是( ).
A.在统计里,把所需考察对象的全体叫作总体
B.一组数据的平均数一定大于这组数据中的每个数据
C.平均数、众数与中位数从不同的角度描述了一组数据的集中趋势
D.一组数据的方差越大,说明这组数据的波动越大
15.数据的方差为,则数据的方差为( ).
A. B. C. D.
二、填空题
16.一个容量为n的样本分成若干组,已知某组的频数和频率分别是30和0.25,则n=________.
17. 从某校2100名学生随机抽取一个30名学生的样本,样本中每个学生用于课外作业的时间(单位:min)依次为:75,80,85,65,95,100,70,55,65,75, 85,110,120,80,85,80,75,90,90,95,70,60,60,75,90,95,65,75,80,80.该校的学生中作业时间超过一个半小时(含一个半小时)的学生有____________人.
18. 频率分布直方图中各小长方体的面积和为____________.
19. 数据-2,-1,0,1,2的方差是____________.
20. 五个数1,2,3,4,a的平均数是3,则a=____,这五个数的标准差是_________.
21. 已知一个样本方差为,则这个样本的容量是____________,平均数是____________.
三、解答题
22.对某电子元件进行寿命追踪调查,情况如下:
寿命(h) 100~200 200~300 300~400 400~500 500~600
个 数 20 30 80 40 30
(1)列出频率分布表; (2)画出频率分布直方图;
(3)估计元件寿命在100~400 h以内的在总体中占的比例;
(4)估计电子元件寿命在400 h以上的在总体中占的比例.
23. 对甲、乙两名自行车赛手在相同条件下进行了6次测试,测得他们的最大速度(m/s)的数据如下表.
甲 27 38 30 37 35 31
乙 33 29 38 34 28 36
(1)画出茎叶图,由茎叶图你能获得哪些信息?
(2)分别求出甲、乙两名自行车赛手最大速度(m/s)数据的平均数、中位数、标准差,并判断选谁参加比赛更合适.
