安徽省合肥市第十六中学2020-2021学年第一学期九年级上册数学模拟测试题(word版无答案)
文档属性
| 名称 | 安徽省合肥市第十六中学2020-2021学年第一学期九年级上册数学模拟测试题(word版无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 146.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-18 00:00:00 | ||
图片预览


文档简介
九年级上册数学期末模拟测试
满分:150分
时间:120分钟
一、单选题(共10小题,每小题4分)
1.
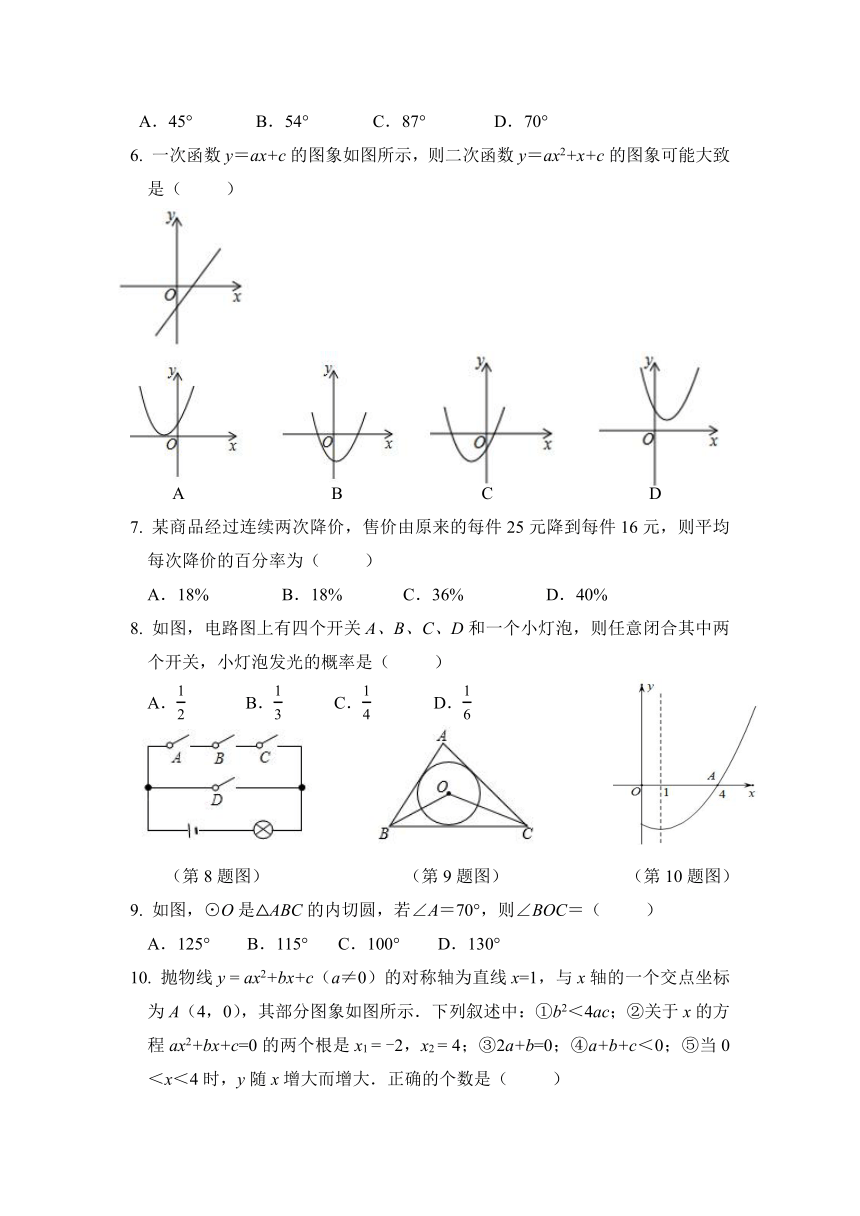
下列所给的汽车标志图案中,既是轴对称图形,又是中心对称图形的是( )
A
B
C
D
2.
下列事件中,为必然事件的是(
)
A.购买一张彩票,中奖
B.打开电视,正在播放广告
C.任意购买一张电影票,座位号恰好是“7排8号”
D.一个袋中只装有5个黑球,从中摸出一个球是黑球
3.
抛物线y
=
(x﹣2)2-1可以由抛物线y
=
x2平移而得到,下列平移正确的是(
)
A.先向左平移2个单位长度,然后向上平移1个单位长度
B.先向左平移2个单位长度,然后向下平移1个单位长度
C.先向右平移2个单位长度,然后向上平移1个单位长度
D.先向右平移2个单位长度,然后向下平移1个单位长度
4.
如图,AB
是⊙O的直径,弦CD⊥AB于点M,若CD=8
cm,MB=2
cm,则直径AB的长为(
)
A.9
cm
B.10
cm
C.11
cm
D.12
cm
(第4题图)
(第5题图)
5.
如图,△ABC中,∠C=63°,将△ABC绕点A顺时针旋转后,得到△AB′C′,且C′
在边BC上,则∠B′C′B的度数为(
)
A.45°
B.54°
C.87°
D.70°
6.
一次函数y=ax+c的图象如图所示,则二次函数y=ax2+x+c的图象可能大致是(
)
A
B
C
D
7.
某商品经过连续两次降价,售价由原来的每件25元降到每件16元,则平均每次降价的百分率为(
)
A.18%
B.18%
C.36%
D.40%
8.
如图,电路图上有四个开关A、B、C、D和一个小灯泡,则任意闭合其中两个开关,小灯泡发光的概率是(
)
A.
B.
C.
D.
(第8题图)
(第9题图)
(第10题图)
9.
如图,⊙O是△ABC的内切圆,若∠A=70°,则∠BOC=(
)
A.125°
B.115°
C.100°
D.130°
10.
抛物线y
=
ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为A(4,0),其部分图象如图所示.下列叙述中:①b2<4ac;②关于x的方程ax2+bx+c=0的两个根是x1
=
-2,x2
=
4;③2a+b=0;④a+b+c<0;⑤当0<x<4时,y随x增大而增大.正确的个数是(
)
A.4
B.3
C.2
D.1
二、填空题(共4小题,每小题5分)
11.
已知m、n分别为的一元二次方程x2
-4x
-1=
0的两个不同实数根,则代数式m2-4m+mn的值为________.
12.
已知二次函数y
=-2(x-1)2+k的图象上有A(-,y1),B(2,y2),C(3,y3)三个点.用“<”连接y1,y2,y3的结果是______.
13.
如图,AB是⊙O的直径,AB=4,点M是OA的中点,过点M的直线与⊙M交于C、D两点,若∠CMA=45°,则弦CD的长为__________.
(第13题图)
(第14题图)
14.
如图,在平面直角坐标系xOy中,P是直线x=2上的一个动点,⊙P的半径为1,直线OQ切⊙P于点Q,则线段OQ的最小值为_______.
三、解答题(共3小题,每小题8分)
15.
解下列方程:
(1)4(x
+
1)2
=
16
(2)x2
-4x
-5
=
0
16.
已知关于x的一元二次方程x2
+
(m+2)x
+
m
-1=
0.
(1)求证:无论m为何值,方程总有两个不相等的实数根;
(2)当m为何值时,该方程两个根的倒数之和等于1.
17.
已知抛物线y
=ax2+bx+c经过(﹣1,0),(0,﹣3),(2,3)三点.
(1)求这条抛物线的表达式;
(2)写出抛物线的开口方向、对称轴和顶点坐标.
四、解答题18、19、20、21题各10分,22题12分,23题14分)
18.
如图,边长为1的正方形组成的网格中,△ABC的顶点均在格点上.点A,B,C的坐标分别是A(4,2),B(2,1),C(4,1).
(1)作出△ABC绕点B顺时针旋转90°以后的图形,并
写出旋转后点A对应点的坐标;
(2)求点A在旋转过程中所经过路径的长度.
19.
如图,△ABC中,∠B=16°,∠ACB=24°,AB=6cm,△ABC按逆时针方向旋转一定角度后与△ADE重合,且点C恰好成为AD的中点.
(1)指出旋转中心,并求出旋转的度数;
(2)求出∠BAE的度数和AE的长.
20.
为落实“垃圾分类”,环卫部门要求垃圾要按A,B,C三类分别装袋,投放,其中A类指废电池,过期药品等有毒垃圾,B类指剩余食品等厨余垃圾,C类指塑料,废纸等可回收垃圾.甲投放了一袋垃圾,乙投放了两袋垃圾,这两袋垃圾不同类.
(1)直接写出甲投放的垃圾恰好是A类的概率;
(2)求乙投放的垃圾恰有一袋与甲投放的垃圾是同类的概率.
21.
如图,AB为⊙O的直径,AC、DC为弦,∠ACD=60°,P为AB延长线上的点,∠APD=30°.
(1)求证:DP是⊙O的切线;
(2)若⊙O的半径为3cm,求图中阴影部分的面积.
22.
旅游公司在景区内配置了50辆观光车供游客租赁使用,假定每辆观光车一天内最多能出租一次,且每辆车的日租金是x元,发现每天的营运规律如下:当x不超过100元时,观光车能全部租出;当x超过100元时,每辆车的日租金每增加5元,租出去的观光车就会减少1辆,已知所有观光车每天的管理费是1000元.
(1)若某日的净收入为5000元,且使游客得到实惠,则当天的观光车的日租金是多少元?(注:净收入=租车收入-
管理费)
(2)设每日净收入为w元,请写出w与x之间的函数关系式;并求出日租金为多少时,每日净收入最大?
23.
如图,抛物线y
=
x2+x-2与x轴交于A、B两点,与y轴交于点C.
(1)求点A,点B和点C的坐标;
(2)在抛物线的对称轴上有一动点P,求PB+PC的值最小时的点P的坐标;
(3)若点M是直线AC下方抛物线上一动点,M点运动到何处时四边形ABCM面积最大,最大面积是多少?
满分:150分
时间:120分钟
一、单选题(共10小题,每小题4分)
1.
下列所给的汽车标志图案中,既是轴对称图形,又是中心对称图形的是( )
A
B
C
D
2.
下列事件中,为必然事件的是(
)
A.购买一张彩票,中奖
B.打开电视,正在播放广告
C.任意购买一张电影票,座位号恰好是“7排8号”
D.一个袋中只装有5个黑球,从中摸出一个球是黑球
3.
抛物线y
=
(x﹣2)2-1可以由抛物线y
=
x2平移而得到,下列平移正确的是(
)
A.先向左平移2个单位长度,然后向上平移1个单位长度
B.先向左平移2个单位长度,然后向下平移1个单位长度
C.先向右平移2个单位长度,然后向上平移1个单位长度
D.先向右平移2个单位长度,然后向下平移1个单位长度
4.
如图,AB
是⊙O的直径,弦CD⊥AB于点M,若CD=8
cm,MB=2
cm,则直径AB的长为(
)
A.9
cm
B.10
cm
C.11
cm
D.12
cm
(第4题图)
(第5题图)
5.
如图,△ABC中,∠C=63°,将△ABC绕点A顺时针旋转后,得到△AB′C′,且C′
在边BC上,则∠B′C′B的度数为(
)
A.45°
B.54°
C.87°
D.70°
6.
一次函数y=ax+c的图象如图所示,则二次函数y=ax2+x+c的图象可能大致是(
)
A
B
C
D
7.
某商品经过连续两次降价,售价由原来的每件25元降到每件16元,则平均每次降价的百分率为(
)
A.18%
B.18%
C.36%
D.40%
8.
如图,电路图上有四个开关A、B、C、D和一个小灯泡,则任意闭合其中两个开关,小灯泡发光的概率是(
)
A.
B.
C.
D.
(第8题图)
(第9题图)
(第10题图)
9.
如图,⊙O是△ABC的内切圆,若∠A=70°,则∠BOC=(
)
A.125°
B.115°
C.100°
D.130°
10.
抛物线y
=
ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为A(4,0),其部分图象如图所示.下列叙述中:①b2<4ac;②关于x的方程ax2+bx+c=0的两个根是x1
=
-2,x2
=
4;③2a+b=0;④a+b+c<0;⑤当0<x<4时,y随x增大而增大.正确的个数是(
)
A.4
B.3
C.2
D.1
二、填空题(共4小题,每小题5分)
11.
已知m、n分别为的一元二次方程x2
-4x
-1=
0的两个不同实数根,则代数式m2-4m+mn的值为________.
12.
已知二次函数y
=-2(x-1)2+k的图象上有A(-,y1),B(2,y2),C(3,y3)三个点.用“<”连接y1,y2,y3的结果是______.
13.
如图,AB是⊙O的直径,AB=4,点M是OA的中点,过点M的直线与⊙M交于C、D两点,若∠CMA=45°,则弦CD的长为__________.
(第13题图)
(第14题图)
14.
如图,在平面直角坐标系xOy中,P是直线x=2上的一个动点,⊙P的半径为1,直线OQ切⊙P于点Q,则线段OQ的最小值为_______.
三、解答题(共3小题,每小题8分)
15.
解下列方程:
(1)4(x
+
1)2
=
16
(2)x2
-4x
-5
=
0
16.
已知关于x的一元二次方程x2
+
(m+2)x
+
m
-1=
0.
(1)求证:无论m为何值,方程总有两个不相等的实数根;
(2)当m为何值时,该方程两个根的倒数之和等于1.
17.
已知抛物线y
=ax2+bx+c经过(﹣1,0),(0,﹣3),(2,3)三点.
(1)求这条抛物线的表达式;
(2)写出抛物线的开口方向、对称轴和顶点坐标.
四、解答题18、19、20、21题各10分,22题12分,23题14分)
18.
如图,边长为1的正方形组成的网格中,△ABC的顶点均在格点上.点A,B,C的坐标分别是A(4,2),B(2,1),C(4,1).
(1)作出△ABC绕点B顺时针旋转90°以后的图形,并
写出旋转后点A对应点的坐标;
(2)求点A在旋转过程中所经过路径的长度.
19.
如图,△ABC中,∠B=16°,∠ACB=24°,AB=6cm,△ABC按逆时针方向旋转一定角度后与△ADE重合,且点C恰好成为AD的中点.
(1)指出旋转中心,并求出旋转的度数;
(2)求出∠BAE的度数和AE的长.
20.
为落实“垃圾分类”,环卫部门要求垃圾要按A,B,C三类分别装袋,投放,其中A类指废电池,过期药品等有毒垃圾,B类指剩余食品等厨余垃圾,C类指塑料,废纸等可回收垃圾.甲投放了一袋垃圾,乙投放了两袋垃圾,这两袋垃圾不同类.
(1)直接写出甲投放的垃圾恰好是A类的概率;
(2)求乙投放的垃圾恰有一袋与甲投放的垃圾是同类的概率.
21.
如图,AB为⊙O的直径,AC、DC为弦,∠ACD=60°,P为AB延长线上的点,∠APD=30°.
(1)求证:DP是⊙O的切线;
(2)若⊙O的半径为3cm,求图中阴影部分的面积.
22.
旅游公司在景区内配置了50辆观光车供游客租赁使用,假定每辆观光车一天内最多能出租一次,且每辆车的日租金是x元,发现每天的营运规律如下:当x不超过100元时,观光车能全部租出;当x超过100元时,每辆车的日租金每增加5元,租出去的观光车就会减少1辆,已知所有观光车每天的管理费是1000元.
(1)若某日的净收入为5000元,且使游客得到实惠,则当天的观光车的日租金是多少元?(注:净收入=租车收入-
管理费)
(2)设每日净收入为w元,请写出w与x之间的函数关系式;并求出日租金为多少时,每日净收入最大?
23.
如图,抛物线y
=
x2+x-2与x轴交于A、B两点,与y轴交于点C.
(1)求点A,点B和点C的坐标;
(2)在抛物线的对称轴上有一动点P,求PB+PC的值最小时的点P的坐标;
(3)若点M是直线AC下方抛物线上一动点,M点运动到何处时四边形ABCM面积最大,最大面积是多少?
同课章节目录
