人教版九年级上册24.1.1 圆的基本概念课件(25张)
文档属性
| 名称 | 人教版九年级上册24.1.1 圆的基本概念课件(25张) |  | |
| 格式 | zip | ||
| 文件大小 | 417.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-19 07:08:03 | ||
图片预览







文档简介
(共25张PPT)
24.1.1
圆的基本概念
“一切立体图形中最美的是球,一切平面图形中最美的是圆”。这是古希腊的数学家毕达哥拉斯一句话。
圆也是一种和谐、美丽的图形,无论从哪个角度看,它都具有同一形状。
圆是生活中常见的图形,许多物体都给我们以圆的形象.
感知圆的世界
生活剪影
一石激起千层浪
奥运五环
福建土楼
乐在其中
小憩片刻
祥子
车轮为什么圆的,而不是椭圆或其他图形?
如图,观察画圆的过程,你能由此说出圆的形成过程吗?
观
察
活动一
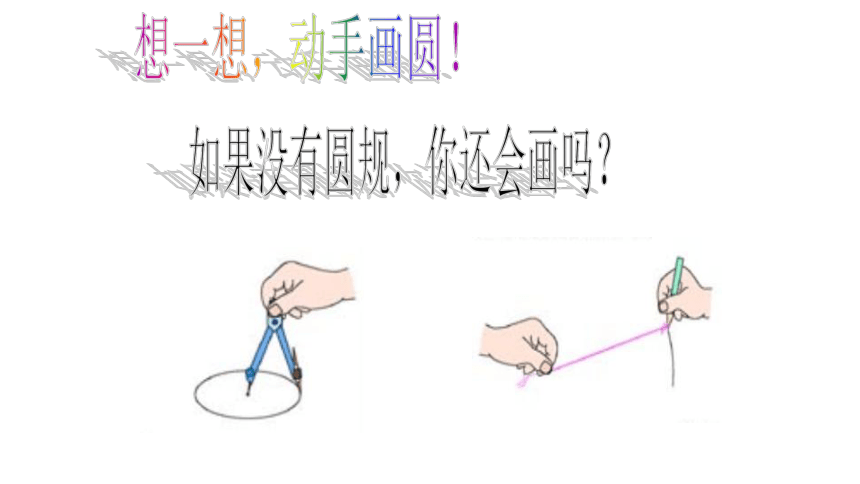
想一想,动手画圆!
如果没有圆规,你还会画吗?
如图,在一个平面内,线段OA绕它固定的一个
端点O旋转一周,另一个端点A所形成的图形叫做圆.
·
r
O
A
固定的端点O叫做圆心
线段OA叫做半径
以点O为圆心的圆,记作“⊙O”,读作“圆O”.
圆的概念
动态定义
讨论下面几个问题并动手画一画:
1.以2厘米为半径能画几个圆?
2.在同一个平面内,以点O为圆心能画几个圆?
3.在同一个平面内,以点O为圆心2厘米为半径,能画几个圆?
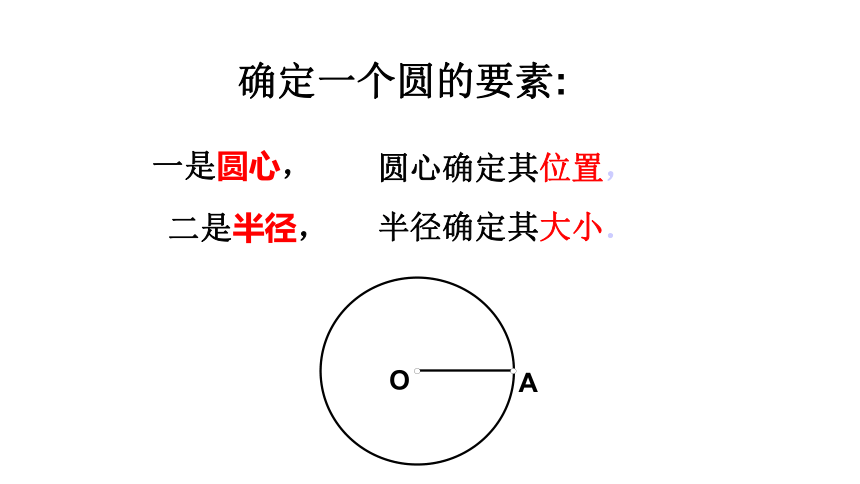
4.确定一个圆由哪几个要素决定?
思
考
确定一个圆由2个要素决定:圆心和半径.
圆心确定圆的位置,半径确定圆的大小.
确定一个圆的要素:
圆心确定其位置,
一是圆心,
二是半径,
半径确定其大小.
1、圆上各点到定点(圆心O)的距离都等于
.
圆心为O、半径为r的圆可以看成是所有到定点O的距离等于定长r
的点的集合.
从画圆的过程可以看出什么呢?
2、到定点的距离等于定长的点都在
.
O
·
A
B
C
E
r
r
r
r
r
D
思
考
定长r
同一个圆上
静态定义:
例题
已知:矩形ABCD的对角线AC、BD相交于O.
求证:A、B、C、D在以O为圆心的同一圆上.
A
B
C
D
O
证明:∵四边形ABCD是矩形
∴AO=OC;OB=OD;
又∵AC=BD
∴OA=OB=OC=OD
∴A、B、C、D在以O为圆心以OA为半径的圆上.
讨论1:
车轮为什么做成圆形?
讨论2:
如果做成正方形会有什么结果?
讨
论
活动二
中心与路面距离相等
中心与边缘距离相等
中心与边缘距离不相等
中心与路面距离不相等
分析
把车轮做成圆形,车轮上各点到车轮中心(圆心)的距离都等于车轮的半径,当车轮在平面上滚动时,车轮中心与平面的距离保持不变,因此,当车辆在平坦的路上行驶时,坐车的人会感觉到非常平稳,这也是车轮都做成圆形的数学道理.
为什么车轮是圆的?
经过圆心的弦(如图中的AB)叫做直径.
·
C
O
A
B
连接圆上任意两点的线段(如图AC)叫做弦,
与圆有关的概念
弦
注意:
1、弦和直径都是线段.
2、直径是弦,是经过圆心的特殊弦,是圆中最长的弦,但弦不一定是直径.
圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
·
C
O
A
B
弧
⌒
圆上任意两点间的部分叫做圆弧,简称弧.以A、C为端点的弧记作
AC
,读作“圆弧AC”或“弧AC”.
·
C
O
A
B
劣弧与优弧
⌒
小于半圆的弧叫做劣弧.
大于半圆的弧叫做优弧.
⌒
(如图中的AC)
(用三个字母表示,如图中的ABC)
等圆与等弧
能够重合的两个圆叫做等圆.
容易看出,半径相等的两个圆是等圆;
在同圆或等圆中,能够互相重合的弧叫做等弧.
反过来,同圆或等圆的半径相等.
判断下列说法的正误:
(1)弦是直径;
(2)半圆是弧;
(3)过圆心的线段是直径;
(4)过圆心的直线是直径;
(5)半圆是最长的弧;
(6)直径是最长的弦;
练
习
(7)半径相等的两个圆是等圆;
(8)长度相等的两条弧是等弧.
如图,请以正确的方式表示出以点A为端点的优弧及劣弧.
练
习
弦与弧
1、请写出图中所有的弦;
2、请任选一条弦,写出这条弦所对的弧;
A
B
C
O
D
练
习
课堂小结
在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点所形成的图形叫做圆.
1.
圆
圆心为O,半径为r的圆是所有到定点O的距离等于定长
r
的点的集合.
静态定义:
动态定义:
·
r
O
A
2.
圆心、半径
固定的端点O叫做圆心.
线段OA叫做半径,一般用r表示.
以点O为圆心的圆,记作“⊙O”,读作“圆O”.
(1)图上各点到定点(圆心O)的距离都等于定长(半径
r
).
(2)到定点的距离等于定长的点都在同一个圆上.
3.
圆的特点
4.
弦、直径
连接圆上任意两点的线段叫做弦.
经过圆心的弦叫做直径.
5.
圆弧(弧)
圆上任意两点间的部分叫做圆弧,简称弧.
再见!
24.1.1
圆的基本概念
“一切立体图形中最美的是球,一切平面图形中最美的是圆”。这是古希腊的数学家毕达哥拉斯一句话。
圆也是一种和谐、美丽的图形,无论从哪个角度看,它都具有同一形状。
圆是生活中常见的图形,许多物体都给我们以圆的形象.
感知圆的世界
生活剪影
一石激起千层浪
奥运五环
福建土楼
乐在其中
小憩片刻
祥子
车轮为什么圆的,而不是椭圆或其他图形?
如图,观察画圆的过程,你能由此说出圆的形成过程吗?
观
察
活动一
想一想,动手画圆!
如果没有圆规,你还会画吗?
如图,在一个平面内,线段OA绕它固定的一个
端点O旋转一周,另一个端点A所形成的图形叫做圆.
·
r
O
A
固定的端点O叫做圆心
线段OA叫做半径
以点O为圆心的圆,记作“⊙O”,读作“圆O”.
圆的概念
动态定义
讨论下面几个问题并动手画一画:
1.以2厘米为半径能画几个圆?
2.在同一个平面内,以点O为圆心能画几个圆?
3.在同一个平面内,以点O为圆心2厘米为半径,能画几个圆?
4.确定一个圆由哪几个要素决定?
思
考
确定一个圆由2个要素决定:圆心和半径.
圆心确定圆的位置,半径确定圆的大小.
确定一个圆的要素:
圆心确定其位置,
一是圆心,
二是半径,
半径确定其大小.
1、圆上各点到定点(圆心O)的距离都等于
.
圆心为O、半径为r的圆可以看成是所有到定点O的距离等于定长r
的点的集合.
从画圆的过程可以看出什么呢?
2、到定点的距离等于定长的点都在
.
O
·
A
B
C
E
r
r
r
r
r
D
思
考
定长r
同一个圆上
静态定义:
例题
已知:矩形ABCD的对角线AC、BD相交于O.
求证:A、B、C、D在以O为圆心的同一圆上.
A
B
C
D
O
证明:∵四边形ABCD是矩形
∴AO=OC;OB=OD;
又∵AC=BD
∴OA=OB=OC=OD
∴A、B、C、D在以O为圆心以OA为半径的圆上.
讨论1:
车轮为什么做成圆形?
讨论2:
如果做成正方形会有什么结果?
讨
论
活动二
中心与路面距离相等
中心与边缘距离相等
中心与边缘距离不相等
中心与路面距离不相等
分析
把车轮做成圆形,车轮上各点到车轮中心(圆心)的距离都等于车轮的半径,当车轮在平面上滚动时,车轮中心与平面的距离保持不变,因此,当车辆在平坦的路上行驶时,坐车的人会感觉到非常平稳,这也是车轮都做成圆形的数学道理.
为什么车轮是圆的?
经过圆心的弦(如图中的AB)叫做直径.
·
C
O
A
B
连接圆上任意两点的线段(如图AC)叫做弦,
与圆有关的概念
弦
注意:
1、弦和直径都是线段.
2、直径是弦,是经过圆心的特殊弦,是圆中最长的弦,但弦不一定是直径.
圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
·
C
O
A
B
弧
⌒
圆上任意两点间的部分叫做圆弧,简称弧.以A、C为端点的弧记作
AC
,读作“圆弧AC”或“弧AC”.
·
C
O
A
B
劣弧与优弧
⌒
小于半圆的弧叫做劣弧.
大于半圆的弧叫做优弧.
⌒
(如图中的AC)
(用三个字母表示,如图中的ABC)
等圆与等弧
能够重合的两个圆叫做等圆.
容易看出,半径相等的两个圆是等圆;
在同圆或等圆中,能够互相重合的弧叫做等弧.
反过来,同圆或等圆的半径相等.
判断下列说法的正误:
(1)弦是直径;
(2)半圆是弧;
(3)过圆心的线段是直径;
(4)过圆心的直线是直径;
(5)半圆是最长的弧;
(6)直径是最长的弦;
练
习
(7)半径相等的两个圆是等圆;
(8)长度相等的两条弧是等弧.
如图,请以正确的方式表示出以点A为端点的优弧及劣弧.
练
习
弦与弧
1、请写出图中所有的弦;
2、请任选一条弦,写出这条弦所对的弧;
A
B
C
O
D
练
习
课堂小结
在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点所形成的图形叫做圆.
1.
圆
圆心为O,半径为r的圆是所有到定点O的距离等于定长
r
的点的集合.
静态定义:
动态定义:
·
r
O
A
2.
圆心、半径
固定的端点O叫做圆心.
线段OA叫做半径,一般用r表示.
以点O为圆心的圆,记作“⊙O”,读作“圆O”.
(1)图上各点到定点(圆心O)的距离都等于定长(半径
r
).
(2)到定点的距离等于定长的点都在同一个圆上.
3.
圆的特点
4.
弦、直径
连接圆上任意两点的线段叫做弦.
经过圆心的弦叫做直径.
5.
圆弧(弧)
圆上任意两点间的部分叫做圆弧,简称弧.
再见!
同课章节目录
