沪科版(2012)初中数学九年级下册 24.4.2 直线与圆的位置关系-切线的判定定理 教案
文档属性
| 名称 | 沪科版(2012)初中数学九年级下册 24.4.2 直线与圆的位置关系-切线的判定定理 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 248.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-19 00:00:00 | ||
图片预览

文档简介
24.4
直线与圆的位置关系
——《切线的判定定理》
【教学目标】:
知识与技能:1.理解切线的判定定理,并学会初步运用.
??
2.知道判定切线的常用的三种方法,初步掌握方法的选择。??????
????
3.掌握在解决切线的问题中常用的辅助线的作法。
过程与方法:
通过复习直线与圆的位置关系,以“d=r直线是圆的切线”为依据,探究切线的判定定理。
情感、态度与价值观:经历观察、探究、证明等数学活动过程,培养学生初步的演绎推理能力,掌握图形的基础知识和基本技能,并能解决简单的问题。
【教学重点】:
探索圆的切线的判定定理,并能运用
【教学难点】:
切线判定定理中所阐述的由位置来判定直线是圆的切线的两大要素:一是经过半径的外端;二是直线垂直于这条半径,利用切线的判定解决几何问题的技巧——辅助线的添加。
【教具】:
三角板、圆规、多媒体课件
【教学过程】:
1、情景导入:
当你在下雨天快速转动雨伞时,
雨水飞出的方向是什么方向呢?
雨水是沿着圆的切线的方向飞出的.
怎样判断一条直线是圆的切线呢?
2、新知探究
思考交流
图中直线l满足什么条件就是⊙O的切线?
方法1:直线与圆只有一个公共点
方法2:圆心到直线的距离等于半径
注意:实际证明过程中,通常不采用方法1;
方法2是从“数量关系”的角度来判定圆的切线的方法。
判定一条直线是不是圆的切线除了这两种方法外还有其它方法吗?
观察与思考
在⊙O上任意作一条半径OA,经过半径外端点A作直线l⊥OA。
(1)
圆心O到直线l的距离d和圆的半径r有什么数量关系?
d=r
(2)
直线
l
和⊙O有什么位置关系呢?
相切
由此你发现直线l满足什么条件,又能得到什么结论呢?
①
直线l经过半径OA的外端点A;
②
直线l垂直于半径0A.
结论:
直线l是⊙O切线
归纳新知:
切线的判定定理:
经过半径外端点并且垂直于这条半径的直线是圆的切线。
对定理的理解:
切线必须同时满足两个条件:
①经过半径外端点;②垂直于这条半径.
定理的数学语言表达:
∵
OA是半径,
l
⊥OA于点A
∴
l是⊙O的切线
判
断:
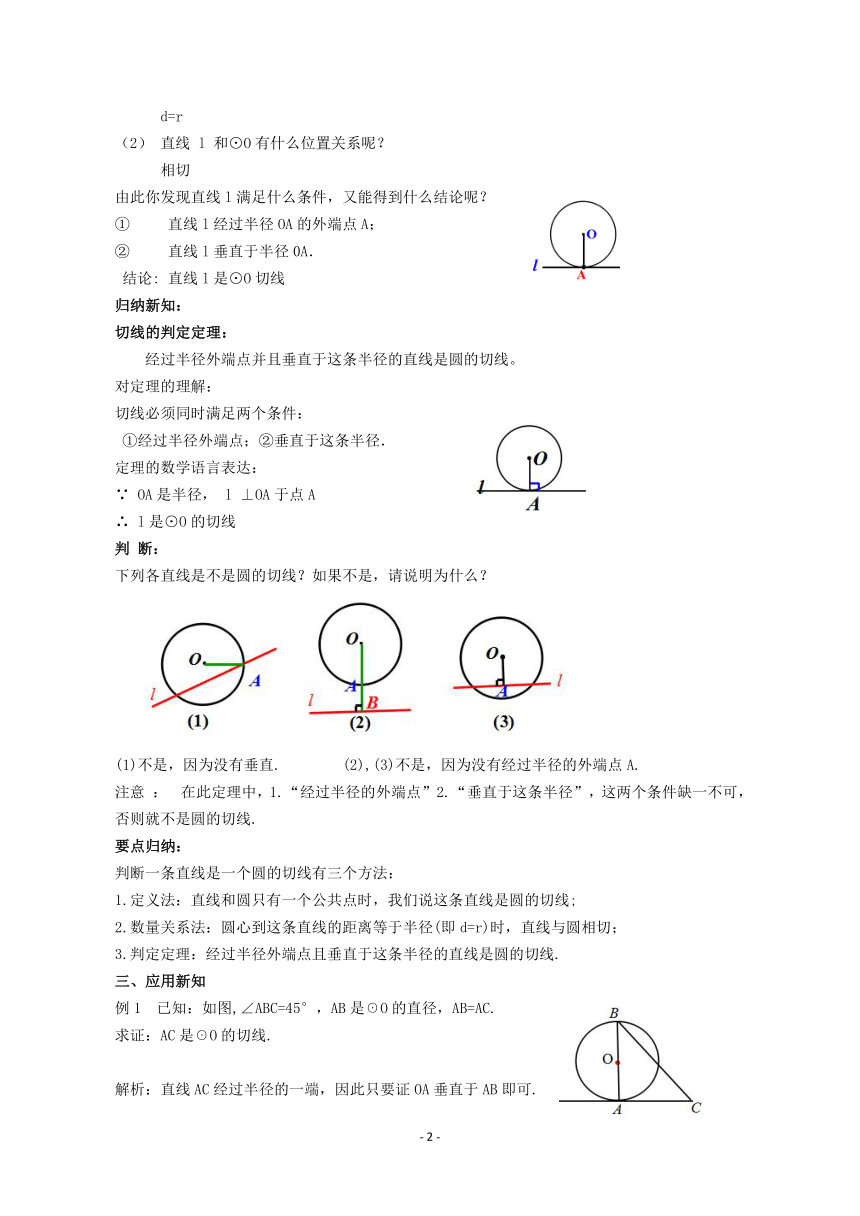
下列各直线是不是圆的切线?如果不是,请说明为什么?
(1)不是,因为没有垂直.
(2),(3)不是,因为没有经过半径的外端点A.
注意
:
在此定理中,1.“经过半径的外端点”2.“垂直于这条半径”,这两个条件缺一不可,否则就不是圆的切线.
要点归纳:
判断一条直线是一个圆的切线有三个方法:
1.定义法:直线和圆只有一个公共点时,我们说这条直线是圆的切线;
2.数量关系法:圆心到这条直线的距离等于半径(即d=r)时,直线与圆相切;
3.判定定理:经过半径外端点且垂直于这条半径的直线是圆的切线.
三、应用新知
例1
已知:如图,∠ABC=45°,AB是☉O的直径,AB=AC.
求证:AC是☉O的切线.
解析:直线AC经过半径的一端,因此只要证OA垂直于AB即可.
证明:∵AB=AC,∠ABC=45°,
∴∠ACB=∠ABC=45°.
∴∠BAC=180°-∠ABC-ACB=90°.
∵AB是☉O的直径,
∴
AC是☉O的切线.
证明直线和圆相切的常见类型①
有交点,连半径,证垂直
例2
如图,已知:O为∠BAC平分线上一点,OD⊥AB于D,以O为圆心,OD为半径作⊙O。
求证:⊙O与AC相切。
证明:过点O作OE⊥AC于点E。
∵
AO平分∠BAC,OD⊥AB
∴
OE=OD
∴
OE是⊙O的半径
∴
AC是⊙O的切线。
证明直线和圆相切的常见类型②
无交点,作垂直,证半径
归
纳:
(1)
如果已知直线经过圆上一点,则连结这点和圆心,得到辅助半径,再证所作半径与这条直线垂直。
简记为:连半径,证垂直。
(2)
(2)如果已知条件中不知直线与圆是否有公共点,则过圆心作直线的垂线段,再证垂线段长等于半径长。
简记为:作垂直,证半径。
四、练习巩固:
1.判断下列命题是否正确.
⑴
经过半径外端的直线是圆的切线.
(
)
⑵
垂直于半径的直线是圆的切
(
)
⑶
过直径的外端并且垂直于这条直径的直线是圆的切线.
(
)
⑷
和圆只有一个公共点的直线是圆的切(
)
⑸
过直径一端点且垂直于直径的直线是圆的切线
(
)
2.如图,AB是⊙O的直径,点D在AB的延长线上,BD=OB,点C在⊙O上,∠CAB=30°,
求证:DC是⊙O的切线.
3.
如图,△ABC中,AB=AC,以AB为直径的☉O交边BC于P,
PE⊥AC于E.
求证:PE是☉O的切线.
4.
如图,OA=OB=5,AB=8,
⊙O的直径为6.
求证:直线AB是⊙O的切
5.如图,AB是⊙O的直径,CD⊥AB,且
OA?=OD·OP.
求证:PC是⊙O的切线.
五、拓展提高
1.已知:△ABC内接于☉O,过点A作直线EF.
(1)如图1,AB为直径,要使EF为☉O的切线,还需添加的条件是(只需写出两种情况):
①
_________
;
②
_____________
.
(2)如图2,AB是非直径的弦,∠CAE=∠B,求证:EF是☉O的切线.
2.如图,已知△ABC,且∠ACB=90°.
(1)请用直尺和圆规按要求作图(保留作图痕迹,不写作法和证明):
①以点A为圆心,BC边的长为半径作⊙A;
②以点B为顶点,在AB边的下方∠ABD=∠BAC.
(2)请判断直线BD与⊙A的位置关系并说明理由.
3.(2018聊城中考)
如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,作ED⊥EB交AB于点D,⊙O是△BED的外接圆.
(1)求证:AC是⊙O的切线;
(2)已知⊙O的半径为2.5,BE=4,求BC,AD的长.
六、课堂小结:?
1.知识:切线的判定定理(两个条件缺一不可).
切线的性质定理
2.方法:判定直线与圆相切的三种方法:
①直线与圆有唯一公共点;
②直线到圆心的距离等于该圆的半径;
③切线的判定定理.即经过半径的外端并且垂直这条半径的直线是圆的切线.
3.证明切线常见辅助线作法:
有交点,连半径,证垂直.
无交点,
作垂直,证半径
7、布置作业
书本P
40
页
5、6
八、板书设计
24.2.2
切线的判定定理
一、知识回顾
二、新知探究
1、切线的判定定理
2、归纳切线的三种判定方法
3、证明切线常用辅助线作法
三、新知应用
四、课堂练习
五、课堂小结
六、布置作业
-
1
-
直线与圆的位置关系
——《切线的判定定理》
【教学目标】:
知识与技能:1.理解切线的判定定理,并学会初步运用.
??
2.知道判定切线的常用的三种方法,初步掌握方法的选择。??????
????
3.掌握在解决切线的问题中常用的辅助线的作法。
过程与方法:
通过复习直线与圆的位置关系,以“d=r直线是圆的切线”为依据,探究切线的判定定理。
情感、态度与价值观:经历观察、探究、证明等数学活动过程,培养学生初步的演绎推理能力,掌握图形的基础知识和基本技能,并能解决简单的问题。
【教学重点】:
探索圆的切线的判定定理,并能运用
【教学难点】:
切线判定定理中所阐述的由位置来判定直线是圆的切线的两大要素:一是经过半径的外端;二是直线垂直于这条半径,利用切线的判定解决几何问题的技巧——辅助线的添加。
【教具】:
三角板、圆规、多媒体课件
【教学过程】:
1、情景导入:
当你在下雨天快速转动雨伞时,
雨水飞出的方向是什么方向呢?
雨水是沿着圆的切线的方向飞出的.
怎样判断一条直线是圆的切线呢?
2、新知探究
思考交流
图中直线l满足什么条件就是⊙O的切线?
方法1:直线与圆只有一个公共点
方法2:圆心到直线的距离等于半径
注意:实际证明过程中,通常不采用方法1;
方法2是从“数量关系”的角度来判定圆的切线的方法。
判定一条直线是不是圆的切线除了这两种方法外还有其它方法吗?
观察与思考
在⊙O上任意作一条半径OA,经过半径外端点A作直线l⊥OA。
(1)
圆心O到直线l的距离d和圆的半径r有什么数量关系?
d=r
(2)
直线
l
和⊙O有什么位置关系呢?
相切
由此你发现直线l满足什么条件,又能得到什么结论呢?
①
直线l经过半径OA的外端点A;
②
直线l垂直于半径0A.
结论:
直线l是⊙O切线
归纳新知:
切线的判定定理:
经过半径外端点并且垂直于这条半径的直线是圆的切线。
对定理的理解:
切线必须同时满足两个条件:
①经过半径外端点;②垂直于这条半径.
定理的数学语言表达:
∵
OA是半径,
l
⊥OA于点A
∴
l是⊙O的切线
判
断:
下列各直线是不是圆的切线?如果不是,请说明为什么?
(1)不是,因为没有垂直.
(2),(3)不是,因为没有经过半径的外端点A.
注意
:
在此定理中,1.“经过半径的外端点”2.“垂直于这条半径”,这两个条件缺一不可,否则就不是圆的切线.
要点归纳:
判断一条直线是一个圆的切线有三个方法:
1.定义法:直线和圆只有一个公共点时,我们说这条直线是圆的切线;
2.数量关系法:圆心到这条直线的距离等于半径(即d=r)时,直线与圆相切;
3.判定定理:经过半径外端点且垂直于这条半径的直线是圆的切线.
三、应用新知
例1
已知:如图,∠ABC=45°,AB是☉O的直径,AB=AC.
求证:AC是☉O的切线.
解析:直线AC经过半径的一端,因此只要证OA垂直于AB即可.
证明:∵AB=AC,∠ABC=45°,
∴∠ACB=∠ABC=45°.
∴∠BAC=180°-∠ABC-ACB=90°.
∵AB是☉O的直径,
∴
AC是☉O的切线.
证明直线和圆相切的常见类型①
有交点,连半径,证垂直
例2
如图,已知:O为∠BAC平分线上一点,OD⊥AB于D,以O为圆心,OD为半径作⊙O。
求证:⊙O与AC相切。
证明:过点O作OE⊥AC于点E。
∵
AO平分∠BAC,OD⊥AB
∴
OE=OD
∴
OE是⊙O的半径
∴
AC是⊙O的切线。
证明直线和圆相切的常见类型②
无交点,作垂直,证半径
归
纳:
(1)
如果已知直线经过圆上一点,则连结这点和圆心,得到辅助半径,再证所作半径与这条直线垂直。
简记为:连半径,证垂直。
(2)
(2)如果已知条件中不知直线与圆是否有公共点,则过圆心作直线的垂线段,再证垂线段长等于半径长。
简记为:作垂直,证半径。
四、练习巩固:
1.判断下列命题是否正确.
⑴
经过半径外端的直线是圆的切线.
(
)
⑵
垂直于半径的直线是圆的切
(
)
⑶
过直径的外端并且垂直于这条直径的直线是圆的切线.
(
)
⑷
和圆只有一个公共点的直线是圆的切(
)
⑸
过直径一端点且垂直于直径的直线是圆的切线
(
)
2.如图,AB是⊙O的直径,点D在AB的延长线上,BD=OB,点C在⊙O上,∠CAB=30°,
求证:DC是⊙O的切线.
3.
如图,△ABC中,AB=AC,以AB为直径的☉O交边BC于P,
PE⊥AC于E.
求证:PE是☉O的切线.
4.
如图,OA=OB=5,AB=8,
⊙O的直径为6.
求证:直线AB是⊙O的切
5.如图,AB是⊙O的直径,CD⊥AB,且
OA?=OD·OP.
求证:PC是⊙O的切线.
五、拓展提高
1.已知:△ABC内接于☉O,过点A作直线EF.
(1)如图1,AB为直径,要使EF为☉O的切线,还需添加的条件是(只需写出两种情况):
①
_________
;
②
_____________
.
(2)如图2,AB是非直径的弦,∠CAE=∠B,求证:EF是☉O的切线.
2.如图,已知△ABC,且∠ACB=90°.
(1)请用直尺和圆规按要求作图(保留作图痕迹,不写作法和证明):
①以点A为圆心,BC边的长为半径作⊙A;
②以点B为顶点,在AB边的下方∠ABD=∠BAC.
(2)请判断直线BD与⊙A的位置关系并说明理由.
3.(2018聊城中考)
如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,作ED⊥EB交AB于点D,⊙O是△BED的外接圆.
(1)求证:AC是⊙O的切线;
(2)已知⊙O的半径为2.5,BE=4,求BC,AD的长.
六、课堂小结:?
1.知识:切线的判定定理(两个条件缺一不可).
切线的性质定理
2.方法:判定直线与圆相切的三种方法:
①直线与圆有唯一公共点;
②直线到圆心的距离等于该圆的半径;
③切线的判定定理.即经过半径的外端并且垂直这条半径的直线是圆的切线.
3.证明切线常见辅助线作法:
有交点,连半径,证垂直.
无交点,
作垂直,证半径
7、布置作业
书本P
40
页
5、6
八、板书设计
24.2.2
切线的判定定理
一、知识回顾
二、新知探究
1、切线的判定定理
2、归纳切线的三种判定方法
3、证明切线常用辅助线作法
三、新知应用
四、课堂练习
五、课堂小结
六、布置作业
-
1
-
