沪科版(2012)初中数学九年级下册 24.4.3直线和圆的位置关系-切线长定理 教案
文档属性
| 名称 | 沪科版(2012)初中数学九年级下册 24.4.3直线和圆的位置关系-切线长定理 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 53.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-19 07:11:29 | ||
图片预览

文档简介
24.4
直线和圆的位置关系(2)切线长定理教学设计
一、教学目标
(一)、知识与技能:
1.理解切线长的概念;
2.掌握切线长定理,并能解决一些简单问题;
3.知道圆外切四边形的性质。
(二)、过程与方法:
1.通过操作、观察两条切线长,发展学生的合情推理能力和演绎推理能力。
2.学生经历知识的形成与运用过程,培养学生的数学语言概括、表达能力。
3.学生探索切线长定理过程中,学会用数形结合思想解决问题。通过运用切线长定理解题,提高学生运用知识和技能解决问题的能力。
(三).情感、态度与价值观
培养学生主动参与探索知识来源,获得数学知识的良好学习习惯,从而提高学生学习数学的积极性。
二、重点、难点:
1.重点:切线长定理的理解;
2.难点:定理的应用。
三、教学方法:
问题及引导发现模式
四、教具及器材:
圆规、三角板;自制课件
五、、教学过程
(一)复习巩固:(放投影,提问)提出问题:
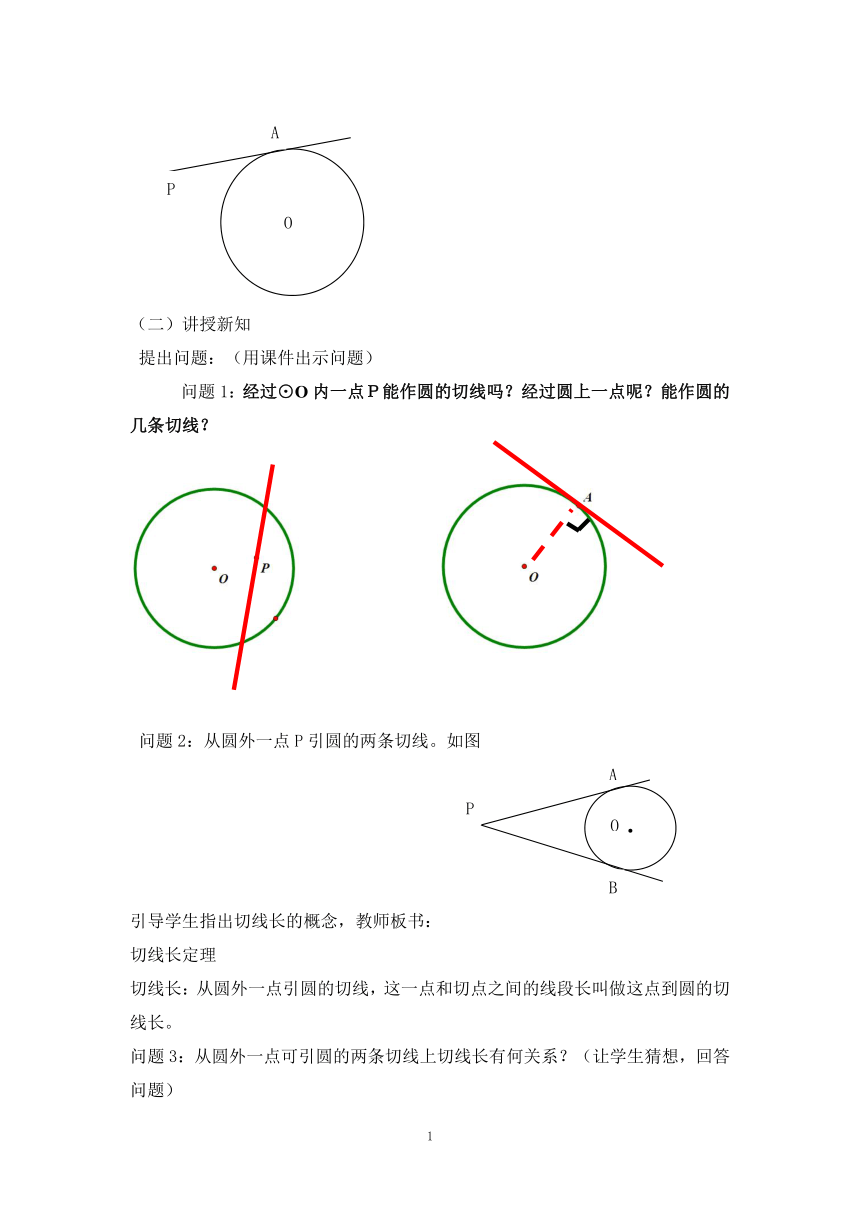
1.如图,PA与⊙O相切于点A,则PA与OA有什么位置关系?
2.切线的判定定理内容是什么?
(二)讲授新知
提出问题:(用课件出示问题)
问题1:经过⊙O内一点P能作圆的切线吗?经过圆上一点呢?能作圆的几条切线?
问题2:从圆外一点P引圆的两条切线。如图
引导学生指出切线长的概念,教师板书:
切线长定理
切线长:从圆外一点引圆的切线,这一点和切点之间的线段长叫做这点到圆的切线长。
问题3:从圆外一点可引圆的两条切线上切线长有何关系?(让学生猜想,回答问题)
它们的切线长相等。
(教师引导学生分析证明猜想)
如图,PA、PB分别与⊙O相切于点A、B
试证明:PA=PB
证明:连结OA、OP、OB
∵
PA、PB与⊙O相切于点A、B
∴
PA⊥OA、PB⊥OB
∴
∠OAP=∠OBP
又∵
OA=OB,OP=OP
∴
Rt△AOP≌Rt△BOP
∴
PA=PB
大家由全等三角形的性质还能得到哪些结论?
(∠OPA=∠OPB等)
问题4:分析问题2的结论及证明,想想我们能得到什么命题?
教师引导学生从条件、结论入手总结“切线长定理”,并板书:
切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。
问题5:如上图,PA、PB分别与⊙O相切于点A、B,若连结AB,则OP与AB又有什么关系?
让学生猜想,教师提问并将定理进行拓展。
例:如图(1),PA、PB分别与⊙O相切于点A、B,直线OP交⊙O于点D、E,交AB于点C。
(1)写出图中所有的垂直关系;
(2)写出图中所有的全等三角形;
(3)写出图中所有的等腰三角形;
(4)如果PA=4cm,PD=2cm,求⊙O的半径OA长。
(5)写出图中所有的相似三角形;
(⑴、⑵提问两名学生回答,⑶(4)(5)让一名学生演板解答。教师简评并设疑“图中有几对相似三角形”)
问题6:如图(2),四边形ABCD的各边分别与⊙O相切于点M、N、P、Q,由切线长定理大家能得到哪些结论?
(提问)
由A点的切线可知_____=_____;
由B点的切线可知_____=_____;
由C点的切线可知_____=_____;
由D点的切线可知_____=_____;
问题6:大家想一想,将上面四个等式左右分别相加,你又能发现什么结论?
引导学生概括“圆外切四边形的性质”,板书:
结论:圆外切四边形的性质:圆外切四边形的两组对边和相等。
(三)、目标检测:(用投影出示问题,让学生思考解答,教师检验)
1.
从圆外一点引圆的切线有____条,这一点和切点之间的线段长叫做这点到圆的________;
2.
从圆外一点引圆的两条切线,它们的切线长____,圆心和这一点的连线平分_______的夹角,并且________两切点的连线;
3.
圆外切四边形的__________相等;
4.
如图(1),PA、PB分别与⊙O相切于点A、B,∠APB=60°,⊙O的半径长为3
cm,则∠APO=_____,OP=____
cm,BP=____
cm,AC=____
cm,AB=____
cm;
5.
如图(2),四边形ABCD外切于⊙O,若AB=5
cm,CD=3
cm,则四边形ABCD的周长为_____
cm。
布置作业:
P41
10、11
(四)、课堂小结:
1.
知识总结:
(1)切线长的概念;
(2)切线长定理及应用.
2.
思想方法:特殊到一般、构造基本图形作辅助线
在解决有关圆的切线长问题时,往往需要我们构建基本图形.
(1)分别连接圆心和切点;
(2)连结两切点;
(3)连结圆心和圆外一点.
课后思考题(见课件)
P
A
O
P
O
·
B
A
P
A
B
O
D
P
A
B
O
C
E
A
B
C
D
M
N
P
Q
图(1)
图(2)
·OOO
O
D
P
A
B
O
C
E
A
B
C
D
M
N
P
Q
图(1)
图(2)
·OOO
O
PAGE
4
直线和圆的位置关系(2)切线长定理教学设计
一、教学目标
(一)、知识与技能:
1.理解切线长的概念;
2.掌握切线长定理,并能解决一些简单问题;
3.知道圆外切四边形的性质。
(二)、过程与方法:
1.通过操作、观察两条切线长,发展学生的合情推理能力和演绎推理能力。
2.学生经历知识的形成与运用过程,培养学生的数学语言概括、表达能力。
3.学生探索切线长定理过程中,学会用数形结合思想解决问题。通过运用切线长定理解题,提高学生运用知识和技能解决问题的能力。
(三).情感、态度与价值观
培养学生主动参与探索知识来源,获得数学知识的良好学习习惯,从而提高学生学习数学的积极性。
二、重点、难点:
1.重点:切线长定理的理解;
2.难点:定理的应用。
三、教学方法:
问题及引导发现模式
四、教具及器材:
圆规、三角板;自制课件
五、、教学过程
(一)复习巩固:(放投影,提问)提出问题:
1.如图,PA与⊙O相切于点A,则PA与OA有什么位置关系?
2.切线的判定定理内容是什么?
(二)讲授新知
提出问题:(用课件出示问题)
问题1:经过⊙O内一点P能作圆的切线吗?经过圆上一点呢?能作圆的几条切线?
问题2:从圆外一点P引圆的两条切线。如图
引导学生指出切线长的概念,教师板书:
切线长定理
切线长:从圆外一点引圆的切线,这一点和切点之间的线段长叫做这点到圆的切线长。
问题3:从圆外一点可引圆的两条切线上切线长有何关系?(让学生猜想,回答问题)
它们的切线长相等。
(教师引导学生分析证明猜想)
如图,PA、PB分别与⊙O相切于点A、B
试证明:PA=PB
证明:连结OA、OP、OB
∵
PA、PB与⊙O相切于点A、B
∴
PA⊥OA、PB⊥OB
∴
∠OAP=∠OBP
又∵
OA=OB,OP=OP
∴
Rt△AOP≌Rt△BOP
∴
PA=PB
大家由全等三角形的性质还能得到哪些结论?
(∠OPA=∠OPB等)
问题4:分析问题2的结论及证明,想想我们能得到什么命题?
教师引导学生从条件、结论入手总结“切线长定理”,并板书:
切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。
问题5:如上图,PA、PB分别与⊙O相切于点A、B,若连结AB,则OP与AB又有什么关系?
让学生猜想,教师提问并将定理进行拓展。
例:如图(1),PA、PB分别与⊙O相切于点A、B,直线OP交⊙O于点D、E,交AB于点C。
(1)写出图中所有的垂直关系;
(2)写出图中所有的全等三角形;
(3)写出图中所有的等腰三角形;
(4)如果PA=4cm,PD=2cm,求⊙O的半径OA长。
(5)写出图中所有的相似三角形;
(⑴、⑵提问两名学生回答,⑶(4)(5)让一名学生演板解答。教师简评并设疑“图中有几对相似三角形”)
问题6:如图(2),四边形ABCD的各边分别与⊙O相切于点M、N、P、Q,由切线长定理大家能得到哪些结论?
(提问)
由A点的切线可知_____=_____;
由B点的切线可知_____=_____;
由C点的切线可知_____=_____;
由D点的切线可知_____=_____;
问题6:大家想一想,将上面四个等式左右分别相加,你又能发现什么结论?
引导学生概括“圆外切四边形的性质”,板书:
结论:圆外切四边形的性质:圆外切四边形的两组对边和相等。
(三)、目标检测:(用投影出示问题,让学生思考解答,教师检验)
1.
从圆外一点引圆的切线有____条,这一点和切点之间的线段长叫做这点到圆的________;
2.
从圆外一点引圆的两条切线,它们的切线长____,圆心和这一点的连线平分_______的夹角,并且________两切点的连线;
3.
圆外切四边形的__________相等;
4.
如图(1),PA、PB分别与⊙O相切于点A、B,∠APB=60°,⊙O的半径长为3
cm,则∠APO=_____,OP=____
cm,BP=____
cm,AC=____
cm,AB=____
cm;
5.
如图(2),四边形ABCD外切于⊙O,若AB=5
cm,CD=3
cm,则四边形ABCD的周长为_____
cm。
布置作业:
P41
10、11
(四)、课堂小结:
1.
知识总结:
(1)切线长的概念;
(2)切线长定理及应用.
2.
思想方法:特殊到一般、构造基本图形作辅助线
在解决有关圆的切线长问题时,往往需要我们构建基本图形.
(1)分别连接圆心和切点;
(2)连结两切点;
(3)连结圆心和圆外一点.
课后思考题(见课件)
P
A
O
P
O
·
B
A
P
A
B
O
D
P
A
B
O
C
E
A
B
C
D
M
N
P
Q
图(1)
图(2)
·OOO
O
D
P
A
B
O
C
E
A
B
C
D
M
N
P
Q
图(1)
图(2)
·OOO
O
PAGE
4
