沪科版(2012)初中数学九年级下册 24.1.1直线与圆的位置关系 教案(表格式)
文档属性
| 名称 | 沪科版(2012)初中数学九年级下册 24.1.1直线与圆的位置关系 教案(表格式) |
|
|
| 格式 | zip | ||
| 文件大小 | 127.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-19 00:00:00 | ||
图片预览

文档简介
学习领域
教材来源
主题名称
直线与圆的位置关系
教学对象
九年级学生
设计教学
新授课
教学时间
授课人:
教学资源
智慧课室软件
能力指标
能够运用数量关系判断直线和圆的位置关系
教学重点
直线和圆的三种位置关系和两种判别方法
教学难点
会根据公共点个数和d与r的关系判断直线和圆的位置关系。
教学目标
理解和掌握直线和圆的位置关系判别方法;会根据公共点个数和d与r的关系判断直线和圆的位置关系。
教学模式
教学流程(P、C)
时间
科技应用(T)
教学评量(P、C)
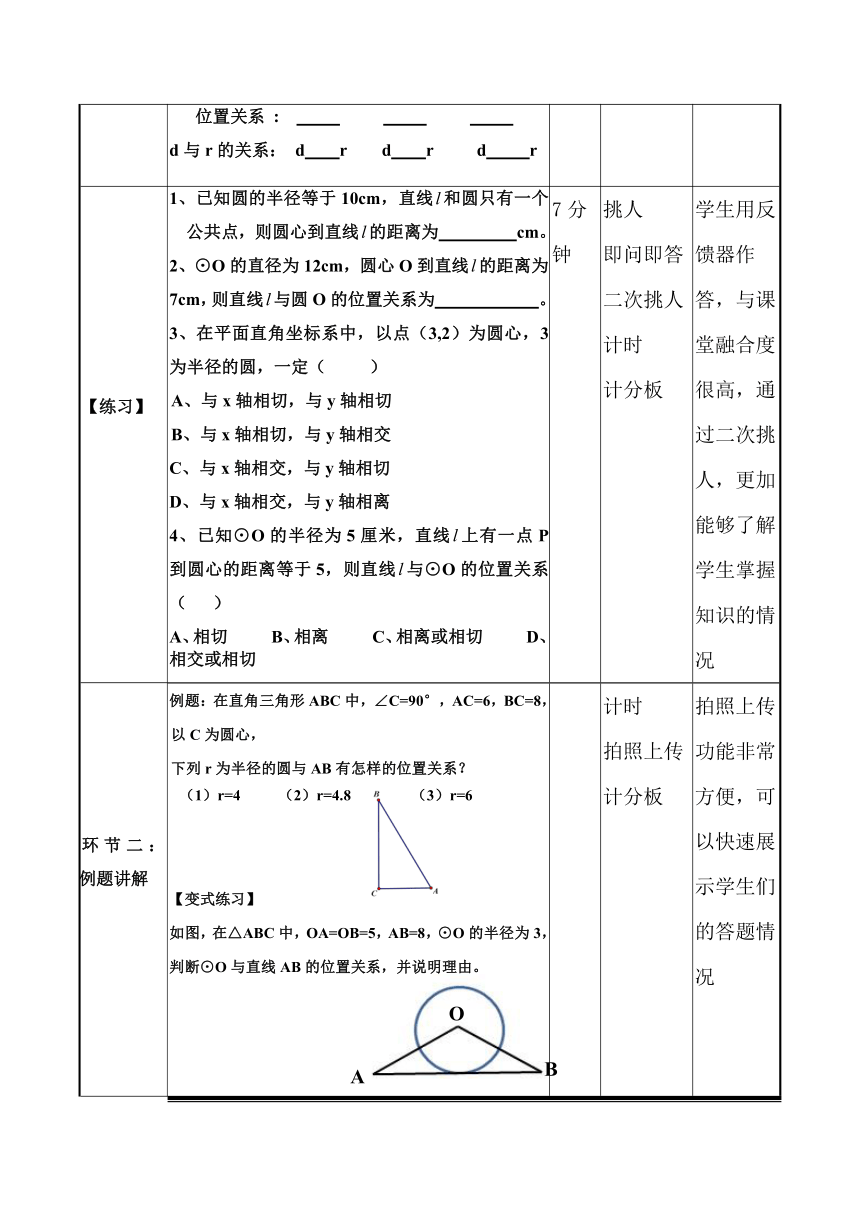
环节一:探索新知
(1)通过预习,我们从公共点的个数变化情况,可以知道直线与圆的位置关系有哪些?公共点:
个
个
个
位置关系:
直线名称:
(2)已知直线,和直线外一点P,请画出点P到直线l的距离d.(4)除了看公共点外,还有什么方法能判断直线与圆的位置关系吗?请分别画出下列三个圆的圆心O与直线的距离d.
7分钟
挑人即问即答计分板计时
学生参与度很高,能够积极使用反馈器作答
位置关系
:
d与r的关系:
d
r
d
r
d
r
【练习】
1、已知圆的半径等于10cm,直线和圆只有一个公共点,则圆心到直线的距离为
cm。2、⊙O的直径为12cm,圆心O到直线的距离为7cm,则直线与圆O的位置关系为
。3、在平面直角坐标系中,以点(3,2)为圆心,3为半径的圆,一定(
)A、与x轴相切,与y轴相切
B、与x轴相切,与y轴相交C、与x轴相交,与y轴相切
D、与x轴相交,与y轴相离4、已知⊙O的半径为5厘米,直线上有一点P到圆心的距离等于5,则直线与⊙O的位置关系(
)A、相切
B、相离
C、相离或相切
D、相交或相切
7分钟
挑人即问即答二次挑人计时计分板
学生用反馈器作答,与课堂融合度很高,通过二次挑人,更加能够了解学生掌握知识的情况
环节二:
例题讲解
例题:在直角三角形ABC中,∠C=90°,AC=6,BC=8,以C为圆心,下列r为半径的圆与AB有怎样的位置关系?(1)r=4
(2)r=4.8
(3)r=6【变式练习】如图,在△ABC中,OA=OB=5,AB=8,⊙O的半径为3,判断⊙O与直线AB的位置关系,并说明理由。
计时拍照上传计分板
拍照上传功能非常方便,可以快速展示学生们的答题情况
【小结提高:】
图形(补充直线)
直线与圆的关系
相离
公共点的个数
1个圆心到直线的距离d与圆的半径r的关系
环节三:巩固练习
1、设⊙O的半径为3,点O到直线的距离为d,若直线与⊙O至少有一个公共
点,则d应满足的条件是(
)。
A、d=3
B、d≤3
C、d<3
D、d>32、与圆有
个公共点的直线是圆的切线;满足d<r,此时的直线是圆的位置关系为
。3、已知直线和⊙O相切,若圆心O到直线的距离是5,则⊙O的半径是
________
。4、在平面直角坐标系中,如果⊙P的圆心P的坐标为(8,0),半径是6,那么y轴与圆的位置关系是
________
。5、如图,在平面直角坐标系中,半径为2的⊙P的圆心P的坐标为(-3,0),将⊙P沿x轴正方向平移,使⊙P与y轴相切,则平移的距离为
。(第5题图)
(第6题图)6、如图,直线AB、CD相交于点O,∠AOC=,半径为1cm的⊙P的圆心在射线OA上,开始时,PO=6cm,如果⊙P以1cm/秒的速度沿由A向B的方向移动,那么当⊙P的运动时间t(秒)满足
时,⊙P与直线CD相交?
计时器挑人抢权计分板
计时器能让学生有做题紧凑的效果,抢权能很好地调动学生的积极性,通过智慧课室多功能的使用,课堂生动,学生参与度高
O
B
A
教材来源
主题名称
直线与圆的位置关系
教学对象
九年级学生
设计教学
新授课
教学时间
授课人:
教学资源
智慧课室软件
能力指标
能够运用数量关系判断直线和圆的位置关系
教学重点
直线和圆的三种位置关系和两种判别方法
教学难点
会根据公共点个数和d与r的关系判断直线和圆的位置关系。
教学目标
理解和掌握直线和圆的位置关系判别方法;会根据公共点个数和d与r的关系判断直线和圆的位置关系。
教学模式
教学流程(P、C)
时间
科技应用(T)
教学评量(P、C)
环节一:探索新知
(1)通过预习,我们从公共点的个数变化情况,可以知道直线与圆的位置关系有哪些?公共点:
个
个
个
位置关系:
直线名称:
(2)已知直线,和直线外一点P,请画出点P到直线l的距离d.(4)除了看公共点外,还有什么方法能判断直线与圆的位置关系吗?请分别画出下列三个圆的圆心O与直线的距离d.
7分钟
挑人即问即答计分板计时
学生参与度很高,能够积极使用反馈器作答
位置关系
:
d与r的关系:
d
r
d
r
d
r
【练习】
1、已知圆的半径等于10cm,直线和圆只有一个公共点,则圆心到直线的距离为
cm。2、⊙O的直径为12cm,圆心O到直线的距离为7cm,则直线与圆O的位置关系为
。3、在平面直角坐标系中,以点(3,2)为圆心,3为半径的圆,一定(
)A、与x轴相切,与y轴相切
B、与x轴相切,与y轴相交C、与x轴相交,与y轴相切
D、与x轴相交,与y轴相离4、已知⊙O的半径为5厘米,直线上有一点P到圆心的距离等于5,则直线与⊙O的位置关系(
)A、相切
B、相离
C、相离或相切
D、相交或相切
7分钟
挑人即问即答二次挑人计时计分板
学生用反馈器作答,与课堂融合度很高,通过二次挑人,更加能够了解学生掌握知识的情况
环节二:
例题讲解
例题:在直角三角形ABC中,∠C=90°,AC=6,BC=8,以C为圆心,下列r为半径的圆与AB有怎样的位置关系?(1)r=4
(2)r=4.8
(3)r=6【变式练习】如图,在△ABC中,OA=OB=5,AB=8,⊙O的半径为3,判断⊙O与直线AB的位置关系,并说明理由。
计时拍照上传计分板
拍照上传功能非常方便,可以快速展示学生们的答题情况
【小结提高:】
图形(补充直线)
直线与圆的关系
相离
公共点的个数
1个圆心到直线的距离d与圆的半径r的关系
环节三:巩固练习
1、设⊙O的半径为3,点O到直线的距离为d,若直线与⊙O至少有一个公共
点,则d应满足的条件是(
)。
A、d=3
B、d≤3
C、d<3
D、d>32、与圆有
个公共点的直线是圆的切线;满足d<r,此时的直线是圆的位置关系为
。3、已知直线和⊙O相切,若圆心O到直线的距离是5,则⊙O的半径是
________
。4、在平面直角坐标系中,如果⊙P的圆心P的坐标为(8,0),半径是6,那么y轴与圆的位置关系是
________
。5、如图,在平面直角坐标系中,半径为2的⊙P的圆心P的坐标为(-3,0),将⊙P沿x轴正方向平移,使⊙P与y轴相切,则平移的距离为
。(第5题图)
(第6题图)6、如图,直线AB、CD相交于点O,∠AOC=,半径为1cm的⊙P的圆心在射线OA上,开始时,PO=6cm,如果⊙P以1cm/秒的速度沿由A向B的方向移动,那么当⊙P的运动时间t(秒)满足
时,⊙P与直线CD相交?
计时器挑人抢权计分板
计时器能让学生有做题紧凑的效果,抢权能很好地调动学生的积极性,通过智慧课室多功能的使用,课堂生动,学生参与度高
O
B
A
