江苏省徐州王杰高级中学2021届高三12月份阶段性检测数学试卷(Word版含解析)
文档属性
| 名称 | 江苏省徐州王杰高级中学2021届高三12月份阶段性检测数学试卷(Word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 586.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-19 10:17:50 | ||
图片预览


文档简介
徐州市王杰中学2020年12月份阶段性检测高中数学试卷
姓名:___________班级:___________得分:___________
一、选择题:(本大题共计16小题,满分64分,每小题4分)
1.已知,则 (? ?)
A. B. C. D.
2.如图,是函数的图象,则函数的单调递减区间是 ( )
A. B. C. D.
3. ( )
A. B. C. D.
4.如图所示,已知、分别为的边、上的中线,设,,则等于 (? ?)
A. B. C. D.
5.若集合,则实数a的取值范围 ( )
A. B. C. D.
6.有20位同学,编号从1至20,现在从中抽取4人作问卷调查,用系统抽样方法确定所抽的编号为(? ???)
A.5,10,15,20????? B.2,6,10,14????? C.2,4,6,8??? ??D.5,8,11,14
7.A公司有10家销售门店,如图为2019年1月B产品的销售数量(单位:包)的茎叶图,则数据落在的概率为 ( )
A. B. C. D.
8.某商店举办有奖销售活动,购物满100元者发兑奖券一张,在10000张奖券中,设特等奖1个,一等奖10个,二等奖100个.若某人购物满100元,那么他中一等奖的概率是 (?? )
A. B. C. D.
9.已知等差数列的前13项之和为39,则等 于 (? ?)
A.6?????????? B.9?????????? C.12????????? D.18
10. ( ?? )
A. B. C. 2 D. 4
11.若,则实数a的取值范围为 ( )
A. B. C. D.
12.直线,若,则a的值为 ( )
A.﹣3或2 B. 3或﹣2 C.﹣3 D.2
13.《九章算术》是我国古代第一部数学专著,它有如下问题:“今有圆堡瑽(cōng),周四丈八尺,高一丈一尺。问积几何?”意思是“今有圆柱体形的土筑小城堡,底面周长为4丈8尺,高1丈1尺。问它的体积是( )?”(注:1丈=10尺,取)
A.704立方尺 B.2112立方尺 C.2115立方尺 D.2118立方尺
14.要得到函数的图象,只需将函数的图象 ( )
A.向左平移个单位 B.向右平移个单位 C.向左平移个单位 D.向右平移个单位
15.已知等比数列中, ,且成等差数列,则 (?? )
A.33 B.72 C.84 D. 189
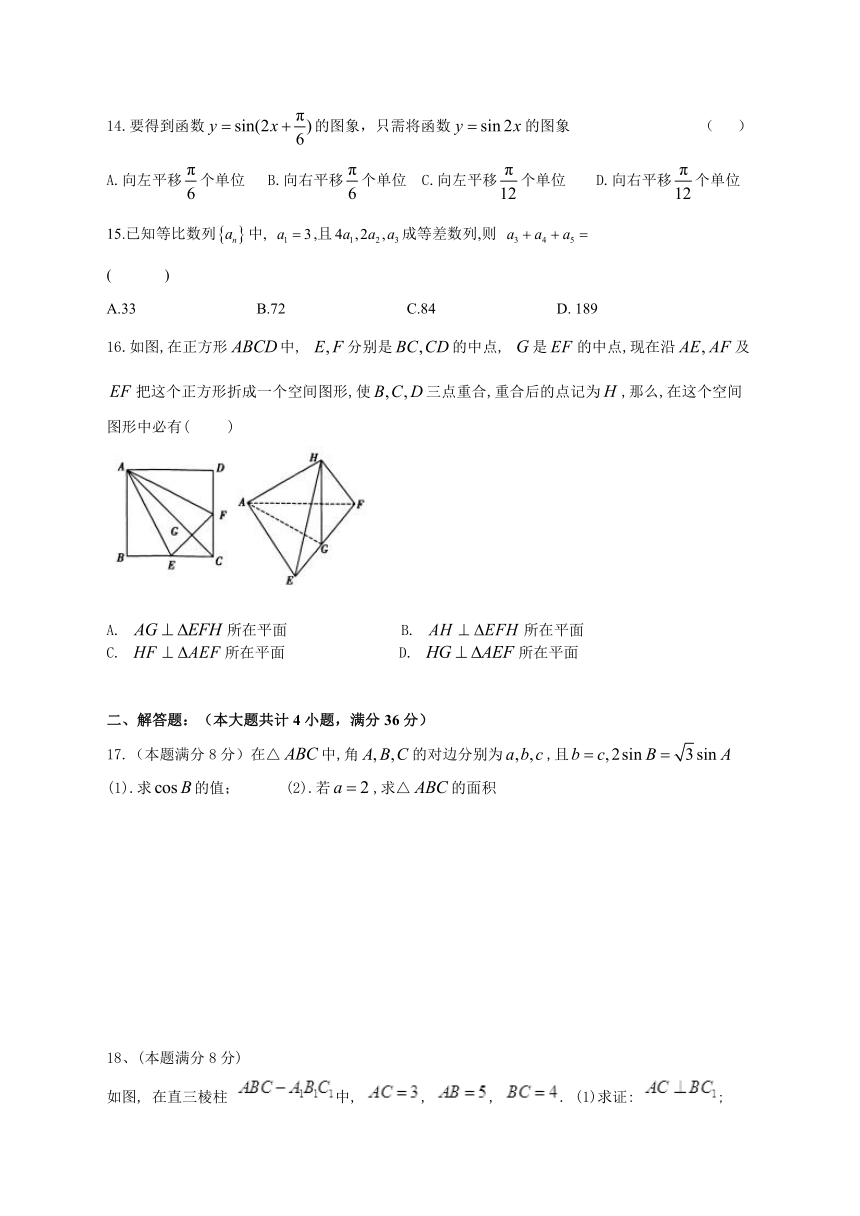
16.如图,在正方形中, 分别是的中点, 是的中点,现在沿及把这个正方形折成一个空间图形,使三点重合,重合后的点记为,那么,在这个空间图形中必有(?? )
A. 所在平面 B. 所在平面
C. 所在平面 D. 所在平面
二、解答题:(本大题共计4小题,满分36分)
17.(本题满分8分)在△中,角的对边分别为,且
(1).求的值; (2).若,求△的面积
18、(本题满分8分)
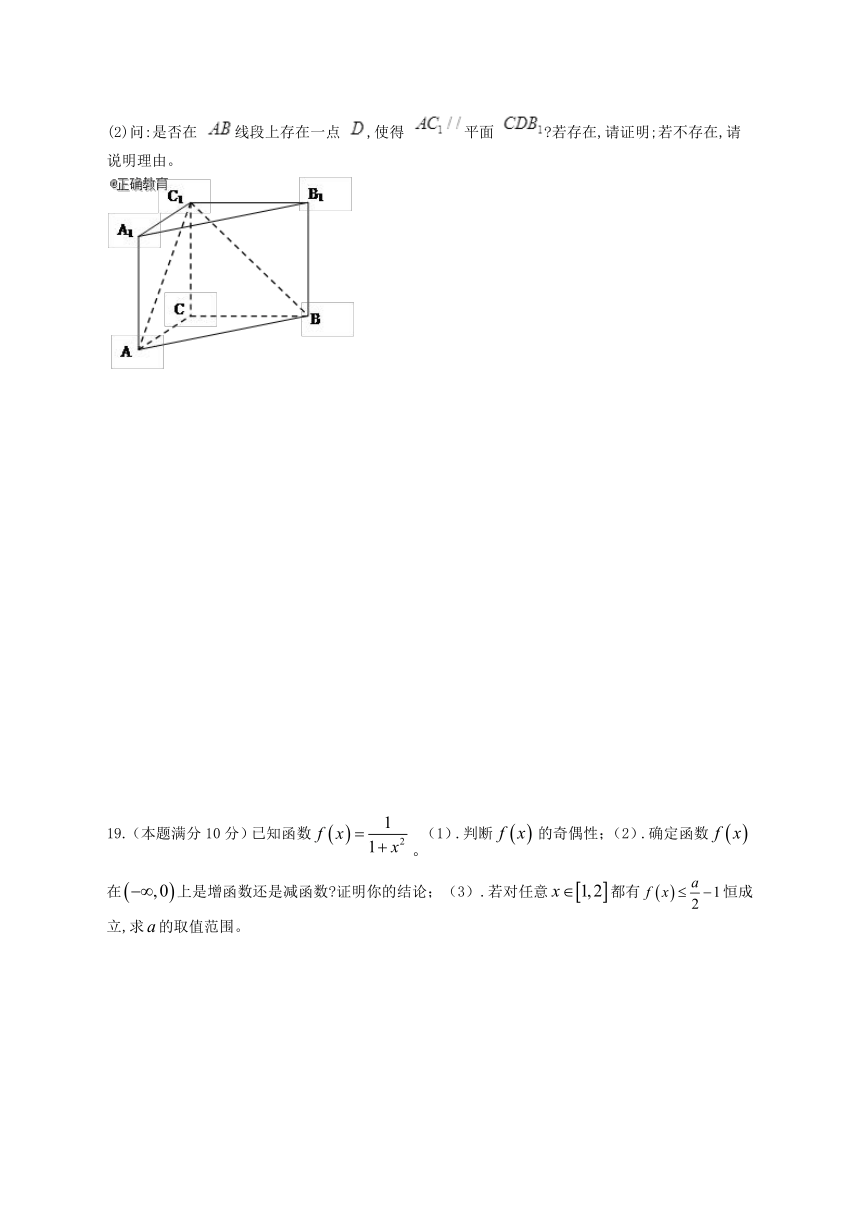
如图, 在直三棱柱 中, , , . (1)求证: ;
(2)问:是否在 线段上存在一点 ,使得 平面 ?若存在,请证明;若不存在,请说明理由。
19.(本题满分10分)已知函数。(1).判断的奇偶性;(2).确定函数在上是增函数还是减函数?证明你的结论;(3).若对任意都有恒成立,求的取值范围。
20.(本题满分10分)已知圆,直线.
(1)求证:直线过定点,且直线与圆相交;
(2)求直线被圆截得的弦长最短时的方程.
参考答案
1.答案:B
解析:联立集合与中方程得:,
解得:,
则,故选B.
2.答案:D
解析:若函数单调递减,则对应的图象为下降的,由图象知,函数在上分别下降,所以对应的单调递减区间为,故选D.
3.答案:D
解析:
4.答案:C
解析: 由题意得,∴.
5.答案:D
解析:
6.答案:A
解析:从20位同学中用系统抽样抽取4人,应分为4组,每组5个,从第一组任取一个编号,然后依次加组间隔5,选A.
7.答案:A
解析:落在内的数据有共6个,所求概率为,故选A.
8.答案:B
解析:中一等奖的概率是.
9.答案:B
解析:由题意,得,所以,解得,所以
10.答案:D
解析:原式.
11.答案:C
解析:,当时,,即;当时,,即.综上,.
12.答案:C
解析:
13.答案:B
解析:设圆柱形城堡的底面半径为尺,高为尺,则尺,∴,
∴城堡的体积立方尺。
故选:B.
14.答案:C
解析:
15.答案:C
解析:由题意可设公比为,则,
又,∴.
∴.
16.答案:B
解析:根据折叠前、后不变,∴平面,B正确;
∵过只有一条直线与平面垂直,A不正确;
∵,∴平面,∴平面平面,
过作直线垂直于平面,一定在平面内,所以C不正确;
∵不垂直于,平面不正确,D不正确.故选B.
17.答案:1.因为,所以.
所以.所以
2.因为,所以.???
又因为,所以.?
所以.
解析:
答案: 18、
解析: 试题分析:(1)利用直三棱柱的性质和底面三角形的特点得到线面垂直, ,进而得到线线垂直。
(2)假设存在点D,满足题意,则由 ,得到线面平行的判定。
证明:⑴、在直三棱柱 ,
∵底面三边长 , , ,
∴ ,
又直三棱柱 中, ,
且 ,
,∴
而 ,∴ ;
⑵、存在, 是 的中点,证明:设 与 的交点为 ,连结 ,
∵ 是 的中点, 是 的中点,∴ ,
∵ , ,∴ .
点评:解决该试题的关键是熟练运用线面垂直的性质定理和线面平行的判定定理来得到证明。对于探索性问题,一般假设存在进行推理论证即可,有的话,要加以说明,并求解出来,不存在说明理由。
19.答案:1.因为函数为,所以定义域为
为偶函数.
2.在区间上取且,
因为,且
,
所以在上为增函数
3. 即可,易得
解析:
20.答案:(1)将点的坐标代入直线的方程,得左边右边,所以直线过定点.
因为,所以点在圆内,所以对任意的实数,直线与圆恒相交.
(2)由平面几何的知识可得,被圆截得的弦最短时与直径垂直,因为,所以此时直线的斜率,所以直线的方程为,即.
解析:
姓名:___________班级:___________得分:___________
一、选择题:(本大题共计16小题,满分64分,每小题4分)
1.已知,则 (? ?)
A. B. C. D.
2.如图,是函数的图象,则函数的单调递减区间是 ( )
A. B. C. D.
3. ( )
A. B. C. D.
4.如图所示,已知、分别为的边、上的中线,设,,则等于 (? ?)
A. B. C. D.
5.若集合,则实数a的取值范围 ( )
A. B. C. D.
6.有20位同学,编号从1至20,现在从中抽取4人作问卷调查,用系统抽样方法确定所抽的编号为(? ???)
A.5,10,15,20????? B.2,6,10,14????? C.2,4,6,8??? ??D.5,8,11,14
7.A公司有10家销售门店,如图为2019年1月B产品的销售数量(单位:包)的茎叶图,则数据落在的概率为 ( )
A. B. C. D.
8.某商店举办有奖销售活动,购物满100元者发兑奖券一张,在10000张奖券中,设特等奖1个,一等奖10个,二等奖100个.若某人购物满100元,那么他中一等奖的概率是 (?? )
A. B. C. D.
9.已知等差数列的前13项之和为39,则等 于 (? ?)
A.6?????????? B.9?????????? C.12????????? D.18
10. ( ?? )
A. B. C. 2 D. 4
11.若,则实数a的取值范围为 ( )
A. B. C. D.
12.直线,若,则a的值为 ( )
A.﹣3或2 B. 3或﹣2 C.﹣3 D.2
13.《九章算术》是我国古代第一部数学专著,它有如下问题:“今有圆堡瑽(cōng),周四丈八尺,高一丈一尺。问积几何?”意思是“今有圆柱体形的土筑小城堡,底面周长为4丈8尺,高1丈1尺。问它的体积是( )?”(注:1丈=10尺,取)
A.704立方尺 B.2112立方尺 C.2115立方尺 D.2118立方尺
14.要得到函数的图象,只需将函数的图象 ( )
A.向左平移个单位 B.向右平移个单位 C.向左平移个单位 D.向右平移个单位
15.已知等比数列中, ,且成等差数列,则 (?? )
A.33 B.72 C.84 D. 189
16.如图,在正方形中, 分别是的中点, 是的中点,现在沿及把这个正方形折成一个空间图形,使三点重合,重合后的点记为,那么,在这个空间图形中必有(?? )
A. 所在平面 B. 所在平面
C. 所在平面 D. 所在平面
二、解答题:(本大题共计4小题,满分36分)
17.(本题满分8分)在△中,角的对边分别为,且
(1).求的值; (2).若,求△的面积
18、(本题满分8分)
如图, 在直三棱柱 中, , , . (1)求证: ;
(2)问:是否在 线段上存在一点 ,使得 平面 ?若存在,请证明;若不存在,请说明理由。
19.(本题满分10分)已知函数。(1).判断的奇偶性;(2).确定函数在上是增函数还是减函数?证明你的结论;(3).若对任意都有恒成立,求的取值范围。
20.(本题满分10分)已知圆,直线.
(1)求证:直线过定点,且直线与圆相交;
(2)求直线被圆截得的弦长最短时的方程.
参考答案
1.答案:B
解析:联立集合与中方程得:,
解得:,
则,故选B.
2.答案:D
解析:若函数单调递减,则对应的图象为下降的,由图象知,函数在上分别下降,所以对应的单调递减区间为,故选D.
3.答案:D
解析:
4.答案:C
解析: 由题意得,∴.
5.答案:D
解析:
6.答案:A
解析:从20位同学中用系统抽样抽取4人,应分为4组,每组5个,从第一组任取一个编号,然后依次加组间隔5,选A.
7.答案:A
解析:落在内的数据有共6个,所求概率为,故选A.
8.答案:B
解析:中一等奖的概率是.
9.答案:B
解析:由题意,得,所以,解得,所以
10.答案:D
解析:原式.
11.答案:C
解析:,当时,,即;当时,,即.综上,.
12.答案:C
解析:
13.答案:B
解析:设圆柱形城堡的底面半径为尺,高为尺,则尺,∴,
∴城堡的体积立方尺。
故选:B.
14.答案:C
解析:
15.答案:C
解析:由题意可设公比为,则,
又,∴.
∴.
16.答案:B
解析:根据折叠前、后不变,∴平面,B正确;
∵过只有一条直线与平面垂直,A不正确;
∵,∴平面,∴平面平面,
过作直线垂直于平面,一定在平面内,所以C不正确;
∵不垂直于,平面不正确,D不正确.故选B.
17.答案:1.因为,所以.
所以.所以
2.因为,所以.???
又因为,所以.?
所以.
解析:
答案: 18、
解析: 试题分析:(1)利用直三棱柱的性质和底面三角形的特点得到线面垂直, ,进而得到线线垂直。
(2)假设存在点D,满足题意,则由 ,得到线面平行的判定。
证明:⑴、在直三棱柱 ,
∵底面三边长 , , ,
∴ ,
又直三棱柱 中, ,
且 ,
,∴
而 ,∴ ;
⑵、存在, 是 的中点,证明:设 与 的交点为 ,连结 ,
∵ 是 的中点, 是 的中点,∴ ,
∵ , ,∴ .
点评:解决该试题的关键是熟练运用线面垂直的性质定理和线面平行的判定定理来得到证明。对于探索性问题,一般假设存在进行推理论证即可,有的话,要加以说明,并求解出来,不存在说明理由。
19.答案:1.因为函数为,所以定义域为
为偶函数.
2.在区间上取且,
因为,且
,
所以在上为增函数
3. 即可,易得
解析:
20.答案:(1)将点的坐标代入直线的方程,得左边右边,所以直线过定点.
因为,所以点在圆内,所以对任意的实数,直线与圆恒相交.
(2)由平面几何的知识可得,被圆截得的弦最短时与直径垂直,因为,所以此时直线的斜率,所以直线的方程为,即.
解析:
同课章节目录
