第三章 变量之间的关系达标检测卷(含答案)
文档属性
| 名称 | 第三章 变量之间的关系达标检测卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-19 08:47:44 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
北师大版七年级数学下册
第三章
达标检测卷
(考试时间:120分钟 满分:120分)
班级:________
姓名:________
分数:________
第Ⅰ卷 (选择题 共30分)
一、选择题(每小题3分,共30分)
1.对于圆的周长公式C=2πR,下列说法中正确的是
( )
A.π,R是变量,2是常量
B.R是变量,π是常量
C.C是变量,π,R是常量
D.C,R是变量,2,π是常量
2.如果每盒圆珠笔有12支,售价18元,用y(元)表示圆珠笔的售价,x(支)表示圆珠笔的数量,那么y与x之间的关系式应该是( )
A.y=12x
B.y=18x
C.y=x
D.y=x
3.已知△ABC的底边BC上的高为8
cm,当它的底边BC从16
cm变化到5
cm时,△ABC的面积( )
A.从20
cm2变化到64
cm2
B.从64
cm2变化到20
cm2
C.从128
cm2变化到40
cm2
D.从40
cm2变化到128
cm2
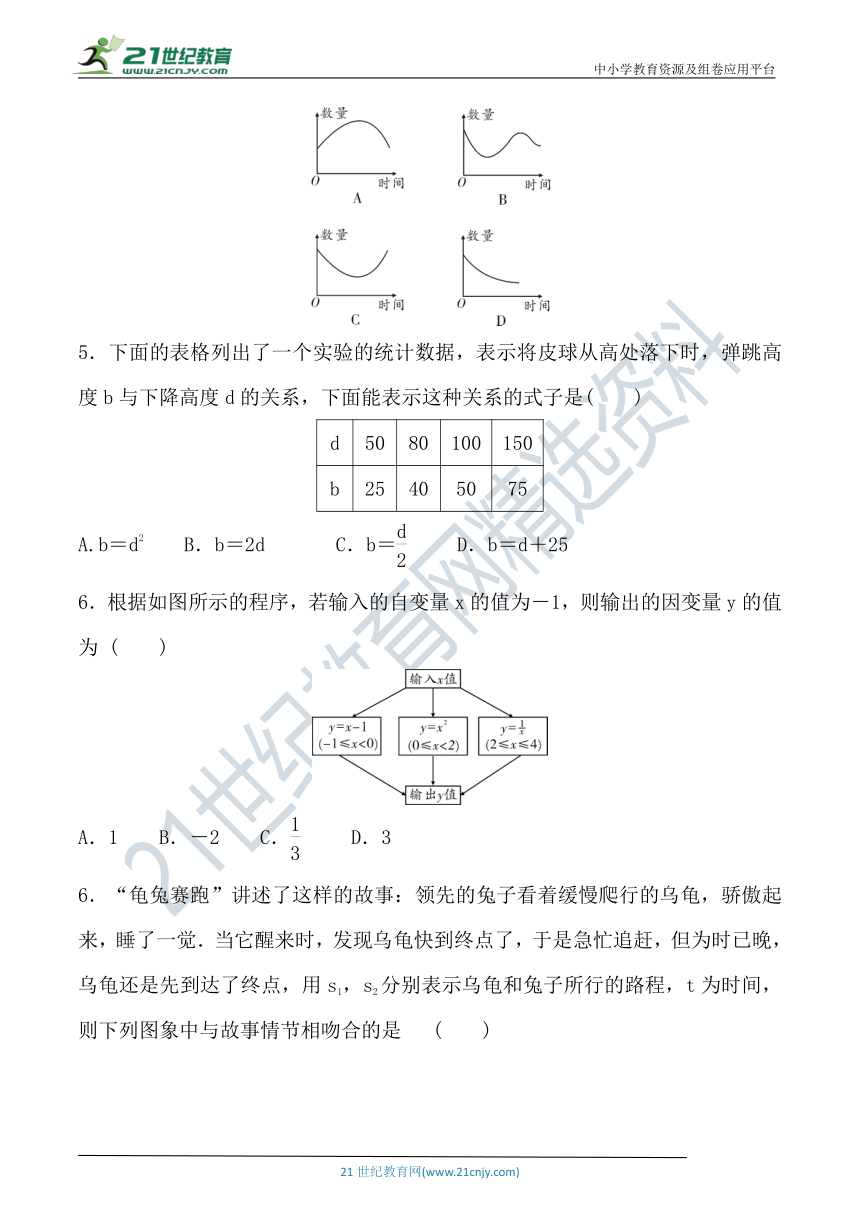
4.前些年,某种野生动物由于人们的滥捕滥杀其数量一直在减少,后来我国加强了对它们的保护,使该野生动物的数量又逐渐增加,下列能够体现这种野生动物的数量和时间的关系的图象是
( )
下面的表格列出了一个实验的统计数据,表示将皮球从高处落下时,弹跳高度b与下降高度d的关系,下面能表示这种关系的式子是( )
d
50
80
100
150
b
25
40
50
75
A.b=d2
B.b=2d
C.b=
D.b=d+25
6.根据如图所示的程序,若输入的自变量x的值为-1,则输出的因变量y的值为
( )
A.1
B.-2
C.
D.3
“龟兔赛跑”讲述了这样的故事:领先的兔子看着缓慢爬行的乌龟,骄傲起来,睡了一觉.当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终点,用s1,s2分别表示乌龟和兔子所行的路程,t为时间,则下列图象中与故事情节相吻合的是
( )
8.由于干旱,某水库的蓄水量随时间的增加而直线下降.若该水库的蓄水量V(万米3)与干旱的时间t(天)的关系如图所示,则下列说法中正确的是( )
A.干旱第50天时,蓄水量为1
200万米3
B.干旱开始后,蓄水量每天增加20万米3
C.干旱开始时,蓄水量为200万米3
D.干旱开始后,蓄水量每天减少20万米3
9.如图,图象(折线OEFPMN)描述了某汽车在行驶过程中速度与时间的关系,下列说法中错误的是( )
A.在第3分时汽车的速度是40千米/时
B.在第12分时汽车的速度是0千米/时
C.从第3分到第6分,汽车停止没有前进
D.从第9分到第12分,汽车的速度从60千米/时减小到0千米/时
10.为了增强抗旱能力,保证今年夏粮丰收,某村新修建了一个蓄水池,这个蓄水池安装了两个进水管和一个出水管(两个进水管的进水速度相同),一个进水管和一个出水管的进出水速度如图①所示,某天0点到6点(至少打开一个水管),该蓄水池的蓄水量如图②所示,并给出以下三个论断:①0点到1点不进水,只出水;②1点到4点不进水,不出水;③4点到6点只进水,不出水.则其中一定正确的论断是( )
eq
\o(\s\up7(),\s\do5(①))
eq
\o(\s\up7(),\s\do5(②))
A.①③
B.②③
C.③
D.①②
第Ⅱ卷 (非选择题 共90分)
二、填空题(每小题3分,共24分)
11.正方形的边长为a,那么它的面积S与a之间的关系式为S=
.
12.拖拉机工作时,油箱中的余油量Q(升)与工作时间t(时)的关系式为Q=40-6t.当t=4时,Q=
.
13.气温日较差是指一天中最高气温与最低气温之差.如图是某地气温日变化曲线图,则在这一天,该地的气温日较差是
.
eq
\o(\s\up7(),\s\do5(第13题图))
eq
\o(\s\up7(),\s\do5(第14题图))
14.如图是某市某天的温度随时间变化的图象,通过观察可知这天
点时温度最高,9点时的温度是
.
15.某城市大剧院地面的一部分为扇形,观众席的座位按下列方式设置:
排数
1
2
3
4
座位数
50
53
56
59
按这种方式排下去,第6排有
个座位.
16.(增城区校级期末)如图所示的是甲、乙两家商店销售同一种产品的销售价y(元)关于销售量x(件)的函数图象.给出下列说法,其中不正确的是
.
①售2件时,甲、乙两家的售价相同;
②买1件时,买乙家的合算;
③买3件时,买甲家的合算;
④乙家的1件售价约为3元.
17.★下面是用棋子摆成的“上”字型图案:
按照以上规律继续摆下去,那么通过观察,可以发现第n个“上”字需用
枚棋子.
18.某市统计局统计了今年第一季度每月人均GDP的增长情况,并绘制了如图所示的统计图,下列结论:①1月份的人均GDP增长率最高;②2月份的人均GDP比1月份低;③这三个月的人均GDP都在增长.其中正确结论的序号是
.
三、解答题(共66分)
19.(6分)某河受暴雨袭击,某天此河水的水位记录如下表:
时间(小时)
0
4
8
12
16
20
24
水位(米)
2
2.5
3
4
5
6
8
(1)上表反映了哪两个变量之间的关系?
(2)12时,水位是多高?
(3)哪一时段水位上升最快?
20.(8分)某校办工厂现在年产值是15万元,计划以后每年增加2万元.
(1)写出年产值y(万元)与年数x之间的关系式;
(2)用表格表示当x从0变化到6(每次增加1)时,y的对应值;
(3)求5年后的年产值.
21.(8分)(张店区期末)某洗衣机在洗涤衣服时,经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量y(L)与时间x(min)之间的关系如折线图所示,根据图象解答下列问题:
(1)洗衣机的进水时间是________分钟,清洗时洗衣机中的水量是________升;
(2)进水时y与x之间的关系式是________;
(3)已知洗衣机的排水速度是每分钟18升,如果排水时间为2分钟,排水结束时洗衣机中剩下的水量是________升.
22.(8分)某药物研究单位试制成功一种新药,经测试,如果患者按规定剂量服用,那么服药后每毫升血液中含药量y(微克)与时间x(时)之间的关系如图所示,如果每毫升血液中的含药量不小于20微克,那么这种药物才能发挥作用,请根据题意回答下列问题:
(1)服药几分钟后,药物开始发挥作用?
(2)服药几小时后,每毫升血液中的含药量最大,最大值是多少微克?
(3)服药后,药物发挥作用的时间有多少小时?
23.(10分)某机动车出发前油箱内有油42
L.行驶若干小时后,途中在加油站加油若干升.油箱中剩余油量Q(L)与行驶时间t(h)之间的关系如图所示,根据图象回答下列问题.
(1)机动车行驶几小时后加油?
(2)中途加油
;
(3)如果加油站距目的地还有240
km,车速为40
km/h,要到达目的地,油箱中的油是否够用?并说明理由.
24.(12分)(竞秀区期末)甲骑摩托车从A地去B地.乙开汽车从B地去A地.同时出发,匀速行驶.各自到达终点后停止.甲、乙两人间的距离s(km)与甲行驶的时间t(h)之间的关系如图所示.
(1)以下是点M,点N,点P所代表的实际意义,请将M,N,P填入对应的横线上:
①甲到达终点:
;
②甲乙两人相遇:
;
③乙到达终点:
;
(2)AB两地之间的路程为
km;
(3)求甲、乙各自的速度;
(4)甲出发几小时后甲、乙两人相距180
km.
25.(14分)一只蚂蚁在一个半圆形的花坛的周边寻找食物,如图①,蚂蚁从圆心O出发,按图中箭头所示的方向,依次匀速爬完线段OA,半圆弧AB,线段BO后,回到出发点.蚂蚁离出发点的距离s(蚂蚁所在位置与O点之间线段的长度)与时间t之间的图象如图②所示.
(1)请直接写出:花坛的半径是________米,a=________;
(2)当t≤2时,求s与t之间的关系式;
(3)若沿途只有一处有食物,蚂蚁在寻找到食物后停下来吃了2分钟,并知蚂蚁在吃食物的前后,始终保持爬行且爬行速度不变,请你求出:
①蚂蚁停下来吃食物的地方离出发点的距离;
②蚂蚁返回O点的时间.(注:圆周率π的值取3)
参考答案
第Ⅰ卷 (选择题 共30分)
一、选择题(每小题3分,共30分)
1.对于圆的周长公式C=2πR,下列说法中正确的是
( D )
A.π,R是变量,2是常量
B.R是变量,π是常量
C.C是变量,π,R是常量
D.C,R是变量,2,π是常量
2.如果每盒圆珠笔有12支,售价18元,用y(元)表示圆珠笔的售价,x(支)表示圆珠笔的数量,那么y与x之间的关系式应该是
( D )
A.y=12x
B.y=18x
C.y=x
D.y=x
3.已知△ABC的底边BC上的高为8
cm,当它的底边BC从16
cm变化到5
cm时,△ABC的面积
( B )
A.从20
cm2变化到64
cm2
B.从64
cm2变化到20
cm2
C.从128
cm2变化到40
cm2
D.从40
cm2变化到128
cm2
4.前些年,某种野生动物由于人们的滥捕滥杀其数量一直在减少,后来我国加强了对它们的保护,使该野生动物的数量又逐渐增加,下列能够体现这种野生动物的数量和时间的关系的图象是
( C )
下面的表格列出了一个实验的统计数据,表示将皮球从高处落下时,弹跳高度b与下降高度d的关系,下面能表示这种关系的式子是
( C )
d
50
80
100
150
b
25
40
50
75
A.b=d2
B.b=2d
C.b=
D.b=d+25
6.根据如图所示的程序,若输入的自变量x的值为-1,则输出的因变量y的值为
( B )
A.1
B.-2
C.
D.3
“龟兔赛跑”讲述了这样的故事:领先的兔子看着缓慢爬行的乌龟,骄傲起来,睡了一觉.当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终点,用s1,s2分别表示乌龟和兔子所行的路程,t为时间,则下列图象中与故事情节相吻合的是
( D )
8.由于干旱,某水库的蓄水量随时间的增加而直线下降.若该水库的蓄水量V(万米3)与干旱的时间t(天)的关系如图所示,则下列说法中正确的是
( D )
A.干旱第50天时,蓄水量为1
200万米3
B.干旱开始后,蓄水量每天增加20万米3
C.干旱开始时,蓄水量为200万米3
D.干旱开始后,蓄水量每天减少20万米3
9.如图,图象(折线OEFPMN)描述了某汽车在行驶过程中速度与时间的关系,下列说法中错误的是
( C )
A.在第3分时汽车的速度是40千米/时
B.在第12分时汽车的速度是0千米/时
C.从第3分到第6分,汽车停止没有前进
D.从第9分到第12分,汽车的速度从60千米/时减小到0千米/时
10.为了增强抗旱能力,保证今年夏粮丰收,某村新修建了一个蓄水池,这个蓄水池安装了两个进水管和一个出水管(两个进水管的进水速度相同),一个进水管和一个出水管的进出水速度如图①所示,某天0点到6点(至少打开一个水管),该蓄水池的蓄水量如图②所示,并给出以下三个论断:①0点到1点不进水,只出水;②1点到4点不进水,不出水;③4点到6点只进水,不出水.则其中一定正确的论断是
( C )
eq
\o(\s\up7(),\s\do5(①))
eq
\o(\s\up7(),\s\do5(②))
A.①③
B.②③
C.③
D.①②
第Ⅱ卷 (非选择题 共90分)
二、填空题(每小题3分,共24分)
11.正方形的边长为a,那么它的面积S与a之间的关系式为S=__a2__.
12.拖拉机工作时,油箱中的余油量Q(升)与工作时间t(时)的关系式为Q=40-6t.当t=4时,Q=__16__.
13.气温日较差是指一天中最高气温与最低气温之差.如图是某地气温日变化曲线图,则在这一天,该地的气温日较差是__11.5_℃__.
eq
\o(\s\up7(),\s\do5(第13题图))
eq
\o(\s\up7(),\s\do5(第14题图))
14.如图是某市某天的温度随时间变化的图象,通过观察可知这天__18__点时温度最高,9点时的温度是__28_℃__.
15.某城市大剧院地面的一部分为扇形,观众席的座位按下列方式设置:
排数
1
2
3
4
座位数
50
53
56
59
按这种方式排下去,第6排有__65__个座位.
16.(增城区校级期末)如图所示的是甲、乙两家商店销售同一种产品的销售价y(元)关于销售量x(件)的函数图象.给出下列说法,其中不正确的是__④__.
①售2件时,甲、乙两家的售价相同;
②买1件时,买乙家的合算;
③买3件时,买甲家的合算;
④乙家的1件售价约为3元.
17.★下面是用棋子摆成的“上”字型图案:
按照以上规律继续摆下去,那么通过观察,可以发现第n个“上”字需用__(4n+2)__枚棋子.
18.某市统计局统计了今年第一季度每月人均GDP的增长情况,并绘制了如图所示的统计图,下列结论:①1月份的人均GDP增长率最高;②2月份的人均GDP比1月份低;③这三个月的人均GDP都在增长.其中正确结论的序号是__①③__.
三、解答题(共66分)
19.(6分)某河受暴雨袭击,某天此河水的水位记录如下表:
时间(小时)
0
4
8
12
16
20
24
水位(米)
2
2.5
3
4
5
6
8
(1)上表反映了哪两个变量之间的关系?
(2)12时,水位是多高?
(3)哪一时段水位上升最快?
解:(1)由表可知,反映了时间和水位之间的关系.
(2)由表可以看出,12时,水位是4米.
(3)由表可以看出,在相等的时间间隔内,20时至24时水位上升最快.
20.(8分)某校办工厂现在年产值是15万元,计划以后每年增加2万元.
(1)写出年产值y(万元)与年数x之间的关系式;
(2)用表格表示当x从0变化到6(每次增加1)时,y的对应值;
(3)求5年后的年产值.
解:(1)关系式为y=2x+15.
(2)列表如下:
x
0
1
2
3
4
5
6
y=2x+15
15
17
19
21
23
25
27
(3)当x=5时,y=2×5+15=25,
∴5年后的年产值是25万元.
21.(8分)(张店区期末)某洗衣机在洗涤衣服时,经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量y(L)与时间x(min)之间的关系如折线图所示,根据图象解答下列问题:
(1)洗衣机的进水时间是________分钟,清洗时洗衣机中的水量是________升;
(2)进水时y与x之间的关系式是________;
(3)已知洗衣机的排水速度是每分钟18升,如果排水时间为2分钟,排水结束时洗衣机中剩下的水量是________升.
解:(1)4,40.
(2)y=10x.
(3)排水结束时洗衣机中剩下的水量是
40-18×2=4(升).
故答案为4.
22.(8分)某药物研究单位试制成功一种新药,经测试,如果患者按规定剂量服用,那么服药后每毫升血液中含药量y(微克)与时间x(时)之间的关系如图所示,如果每毫升血液中的含药量不小于20微克,那么这种药物才能发挥作用,请根据题意回答下列问题:
(1)服药几分钟后,药物开始发挥作用?
(2)服药几小时后,每毫升血液中的含药量最大,最大值是多少微克?
(3)服药后,药物发挥作用的时间有多少小时?
解:(1)服药20分钟后,药物开始发挥作用.
(2)服药2小时后,每毫升血液中的含药量最大,最大值是80微克.
(3)药物发挥作用的时间有6小时.
23.(10分)某机动车出发前油箱内有油42
L.行驶若干小时后,途中在加油站加油若干升.油箱中剩余油量Q(L)与行驶时间t(h)之间的关系如图所示,根据图象回答下列问题.
(1)机动车行驶几小时后加油?
(2)中途加油__24L__;
(3)如果加油站距目的地还有240
km,车速为40
km/h,要到达目的地,油箱中的油是否够用?并说明理由.
解:(1)由图知,5
h后加油.
(3)油箱中的油够用.理由:因为机动车每小时耗油(42-12)÷5=6
L,
所以240÷40×6=36
L,正好到达.
24.(12分)(竞秀区期末)甲骑摩托车从A地去B地.乙开汽车从B地去A地.同时出发,匀速行驶.各自到达终点后停止.甲、乙两人间的距离s(km)与甲行驶的时间t(h)之间的关系如图所示.
(1)以下是点M,点N,点P所代表的实际意义,请将M,N,P填入对应的横线上:
①甲到达终点:__P__;
②甲乙两人相遇:__M__;
③乙到达终点:__N__;
(2)AB两地之间的路程为__240__km;
(3)求甲、乙各自的速度;
(4)甲出发几小时后甲、乙两人相距180
km.
解:(3)甲的速度:
240÷6=40(km/h),
乙的速度:
240÷2-40=80(km/h).
(4)①相遇之前:
(240-180)÷(40+80)=0.5(h);
②相遇之后:
3+(180-120)÷40=4.5(h).
综上所述,甲出发0.5
h或4.5
h后,甲、乙两人相距180
km.
25.(14分)一只蚂蚁在一个半圆形的花坛的周边寻找食物,如图①,蚂蚁从圆心O出发,按图中箭头所示的方向,依次匀速爬完线段OA,半圆弧AB,线段BO后,回到出发点.蚂蚁离出发点的距离s(蚂蚁所在位置与O点之间线段的长度)与时间t之间的图象如图②所示.
(1)请直接写出:花坛的半径是________米,a=________;
(2)当t≤2时,求s与t之间的关系式;
(3)若沿途只有一处有食物,蚂蚁在寻找到食物后停下来吃了2分钟,并知蚂蚁在吃食物的前后,始终保持爬行且爬行速度不变,请你求出:
①蚂蚁停下来吃食物的地方离出发点的距离;
②蚂蚁返回O点的时间.(注:圆周率π的值取3)
解:(1)由图可知,花坛的半径是4米,
蚂蚁的速度为4÷2=2(米/分),
a=(4+4π)÷2=(4+4×3)÷2=8.
故答案为:4;8.
(2)由图象,可知当t=0时,s=0;
当t=2时,s=4,
∴s=2t(t≤2).
(3)①∵沿途只有一处食物,
∴蚂蚁只能在BO段吃食物,11-8-2=1,
∴蚂蚁从B爬1分钟找到食物,
4-1×2=2(米),
∴蚂蚁停下来吃食物的地方距出发点2米;
②∵蚂蚁停下来吃食的地方距出发点2米,
2÷2=1(分钟),11+1=12(分钟),
∴蚂蚁返回O点的时间为12分钟.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
北师大版七年级数学下册
第三章
达标检测卷
(考试时间:120分钟 满分:120分)
班级:________
姓名:________
分数:________
第Ⅰ卷 (选择题 共30分)
一、选择题(每小题3分,共30分)
1.对于圆的周长公式C=2πR,下列说法中正确的是
( )
A.π,R是变量,2是常量
B.R是变量,π是常量
C.C是变量,π,R是常量
D.C,R是变量,2,π是常量
2.如果每盒圆珠笔有12支,售价18元,用y(元)表示圆珠笔的售价,x(支)表示圆珠笔的数量,那么y与x之间的关系式应该是( )
A.y=12x
B.y=18x
C.y=x
D.y=x
3.已知△ABC的底边BC上的高为8
cm,当它的底边BC从16
cm变化到5
cm时,△ABC的面积( )
A.从20
cm2变化到64
cm2
B.从64
cm2变化到20
cm2
C.从128
cm2变化到40
cm2
D.从40
cm2变化到128
cm2
4.前些年,某种野生动物由于人们的滥捕滥杀其数量一直在减少,后来我国加强了对它们的保护,使该野生动物的数量又逐渐增加,下列能够体现这种野生动物的数量和时间的关系的图象是
( )
下面的表格列出了一个实验的统计数据,表示将皮球从高处落下时,弹跳高度b与下降高度d的关系,下面能表示这种关系的式子是( )
d
50
80
100
150
b
25
40
50
75
A.b=d2
B.b=2d
C.b=
D.b=d+25
6.根据如图所示的程序,若输入的自变量x的值为-1,则输出的因变量y的值为
( )
A.1
B.-2
C.
D.3
“龟兔赛跑”讲述了这样的故事:领先的兔子看着缓慢爬行的乌龟,骄傲起来,睡了一觉.当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终点,用s1,s2分别表示乌龟和兔子所行的路程,t为时间,则下列图象中与故事情节相吻合的是
( )
8.由于干旱,某水库的蓄水量随时间的增加而直线下降.若该水库的蓄水量V(万米3)与干旱的时间t(天)的关系如图所示,则下列说法中正确的是( )
A.干旱第50天时,蓄水量为1
200万米3
B.干旱开始后,蓄水量每天增加20万米3
C.干旱开始时,蓄水量为200万米3
D.干旱开始后,蓄水量每天减少20万米3
9.如图,图象(折线OEFPMN)描述了某汽车在行驶过程中速度与时间的关系,下列说法中错误的是( )
A.在第3分时汽车的速度是40千米/时
B.在第12分时汽车的速度是0千米/时
C.从第3分到第6分,汽车停止没有前进
D.从第9分到第12分,汽车的速度从60千米/时减小到0千米/时
10.为了增强抗旱能力,保证今年夏粮丰收,某村新修建了一个蓄水池,这个蓄水池安装了两个进水管和一个出水管(两个进水管的进水速度相同),一个进水管和一个出水管的进出水速度如图①所示,某天0点到6点(至少打开一个水管),该蓄水池的蓄水量如图②所示,并给出以下三个论断:①0点到1点不进水,只出水;②1点到4点不进水,不出水;③4点到6点只进水,不出水.则其中一定正确的论断是( )
eq
\o(\s\up7(),\s\do5(①))
eq
\o(\s\up7(),\s\do5(②))
A.①③
B.②③
C.③
D.①②
第Ⅱ卷 (非选择题 共90分)
二、填空题(每小题3分,共24分)
11.正方形的边长为a,那么它的面积S与a之间的关系式为S=
.
12.拖拉机工作时,油箱中的余油量Q(升)与工作时间t(时)的关系式为Q=40-6t.当t=4时,Q=
.
13.气温日较差是指一天中最高气温与最低气温之差.如图是某地气温日变化曲线图,则在这一天,该地的气温日较差是
.
eq
\o(\s\up7(),\s\do5(第13题图))
eq
\o(\s\up7(),\s\do5(第14题图))
14.如图是某市某天的温度随时间变化的图象,通过观察可知这天
点时温度最高,9点时的温度是
.
15.某城市大剧院地面的一部分为扇形,观众席的座位按下列方式设置:
排数
1
2
3
4
座位数
50
53
56
59
按这种方式排下去,第6排有
个座位.
16.(增城区校级期末)如图所示的是甲、乙两家商店销售同一种产品的销售价y(元)关于销售量x(件)的函数图象.给出下列说法,其中不正确的是
.
①售2件时,甲、乙两家的售价相同;
②买1件时,买乙家的合算;
③买3件时,买甲家的合算;
④乙家的1件售价约为3元.
17.★下面是用棋子摆成的“上”字型图案:
按照以上规律继续摆下去,那么通过观察,可以发现第n个“上”字需用
枚棋子.
18.某市统计局统计了今年第一季度每月人均GDP的增长情况,并绘制了如图所示的统计图,下列结论:①1月份的人均GDP增长率最高;②2月份的人均GDP比1月份低;③这三个月的人均GDP都在增长.其中正确结论的序号是
.
三、解答题(共66分)
19.(6分)某河受暴雨袭击,某天此河水的水位记录如下表:
时间(小时)
0
4
8
12
16
20
24
水位(米)
2
2.5
3
4
5
6
8
(1)上表反映了哪两个变量之间的关系?
(2)12时,水位是多高?
(3)哪一时段水位上升最快?
20.(8分)某校办工厂现在年产值是15万元,计划以后每年增加2万元.
(1)写出年产值y(万元)与年数x之间的关系式;
(2)用表格表示当x从0变化到6(每次增加1)时,y的对应值;
(3)求5年后的年产值.
21.(8分)(张店区期末)某洗衣机在洗涤衣服时,经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量y(L)与时间x(min)之间的关系如折线图所示,根据图象解答下列问题:
(1)洗衣机的进水时间是________分钟,清洗时洗衣机中的水量是________升;
(2)进水时y与x之间的关系式是________;
(3)已知洗衣机的排水速度是每分钟18升,如果排水时间为2分钟,排水结束时洗衣机中剩下的水量是________升.
22.(8分)某药物研究单位试制成功一种新药,经测试,如果患者按规定剂量服用,那么服药后每毫升血液中含药量y(微克)与时间x(时)之间的关系如图所示,如果每毫升血液中的含药量不小于20微克,那么这种药物才能发挥作用,请根据题意回答下列问题:
(1)服药几分钟后,药物开始发挥作用?
(2)服药几小时后,每毫升血液中的含药量最大,最大值是多少微克?
(3)服药后,药物发挥作用的时间有多少小时?
23.(10分)某机动车出发前油箱内有油42
L.行驶若干小时后,途中在加油站加油若干升.油箱中剩余油量Q(L)与行驶时间t(h)之间的关系如图所示,根据图象回答下列问题.
(1)机动车行驶几小时后加油?
(2)中途加油
;
(3)如果加油站距目的地还有240
km,车速为40
km/h,要到达目的地,油箱中的油是否够用?并说明理由.
24.(12分)(竞秀区期末)甲骑摩托车从A地去B地.乙开汽车从B地去A地.同时出发,匀速行驶.各自到达终点后停止.甲、乙两人间的距离s(km)与甲行驶的时间t(h)之间的关系如图所示.
(1)以下是点M,点N,点P所代表的实际意义,请将M,N,P填入对应的横线上:
①甲到达终点:
;
②甲乙两人相遇:
;
③乙到达终点:
;
(2)AB两地之间的路程为
km;
(3)求甲、乙各自的速度;
(4)甲出发几小时后甲、乙两人相距180
km.
25.(14分)一只蚂蚁在一个半圆形的花坛的周边寻找食物,如图①,蚂蚁从圆心O出发,按图中箭头所示的方向,依次匀速爬完线段OA,半圆弧AB,线段BO后,回到出发点.蚂蚁离出发点的距离s(蚂蚁所在位置与O点之间线段的长度)与时间t之间的图象如图②所示.
(1)请直接写出:花坛的半径是________米,a=________;
(2)当t≤2时,求s与t之间的关系式;
(3)若沿途只有一处有食物,蚂蚁在寻找到食物后停下来吃了2分钟,并知蚂蚁在吃食物的前后,始终保持爬行且爬行速度不变,请你求出:
①蚂蚁停下来吃食物的地方离出发点的距离;
②蚂蚁返回O点的时间.(注:圆周率π的值取3)
参考答案
第Ⅰ卷 (选择题 共30分)
一、选择题(每小题3分,共30分)
1.对于圆的周长公式C=2πR,下列说法中正确的是
( D )
A.π,R是变量,2是常量
B.R是变量,π是常量
C.C是变量,π,R是常量
D.C,R是变量,2,π是常量
2.如果每盒圆珠笔有12支,售价18元,用y(元)表示圆珠笔的售价,x(支)表示圆珠笔的数量,那么y与x之间的关系式应该是
( D )
A.y=12x
B.y=18x
C.y=x
D.y=x
3.已知△ABC的底边BC上的高为8
cm,当它的底边BC从16
cm变化到5
cm时,△ABC的面积
( B )
A.从20
cm2变化到64
cm2
B.从64
cm2变化到20
cm2
C.从128
cm2变化到40
cm2
D.从40
cm2变化到128
cm2
4.前些年,某种野生动物由于人们的滥捕滥杀其数量一直在减少,后来我国加强了对它们的保护,使该野生动物的数量又逐渐增加,下列能够体现这种野生动物的数量和时间的关系的图象是
( C )
下面的表格列出了一个实验的统计数据,表示将皮球从高处落下时,弹跳高度b与下降高度d的关系,下面能表示这种关系的式子是
( C )
d
50
80
100
150
b
25
40
50
75
A.b=d2
B.b=2d
C.b=
D.b=d+25
6.根据如图所示的程序,若输入的自变量x的值为-1,则输出的因变量y的值为
( B )
A.1
B.-2
C.
D.3
“龟兔赛跑”讲述了这样的故事:领先的兔子看着缓慢爬行的乌龟,骄傲起来,睡了一觉.当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终点,用s1,s2分别表示乌龟和兔子所行的路程,t为时间,则下列图象中与故事情节相吻合的是
( D )
8.由于干旱,某水库的蓄水量随时间的增加而直线下降.若该水库的蓄水量V(万米3)与干旱的时间t(天)的关系如图所示,则下列说法中正确的是
( D )
A.干旱第50天时,蓄水量为1
200万米3
B.干旱开始后,蓄水量每天增加20万米3
C.干旱开始时,蓄水量为200万米3
D.干旱开始后,蓄水量每天减少20万米3
9.如图,图象(折线OEFPMN)描述了某汽车在行驶过程中速度与时间的关系,下列说法中错误的是
( C )
A.在第3分时汽车的速度是40千米/时
B.在第12分时汽车的速度是0千米/时
C.从第3分到第6分,汽车停止没有前进
D.从第9分到第12分,汽车的速度从60千米/时减小到0千米/时
10.为了增强抗旱能力,保证今年夏粮丰收,某村新修建了一个蓄水池,这个蓄水池安装了两个进水管和一个出水管(两个进水管的进水速度相同),一个进水管和一个出水管的进出水速度如图①所示,某天0点到6点(至少打开一个水管),该蓄水池的蓄水量如图②所示,并给出以下三个论断:①0点到1点不进水,只出水;②1点到4点不进水,不出水;③4点到6点只进水,不出水.则其中一定正确的论断是
( C )
eq
\o(\s\up7(),\s\do5(①))
eq
\o(\s\up7(),\s\do5(②))
A.①③
B.②③
C.③
D.①②
第Ⅱ卷 (非选择题 共90分)
二、填空题(每小题3分,共24分)
11.正方形的边长为a,那么它的面积S与a之间的关系式为S=__a2__.
12.拖拉机工作时,油箱中的余油量Q(升)与工作时间t(时)的关系式为Q=40-6t.当t=4时,Q=__16__.
13.气温日较差是指一天中最高气温与最低气温之差.如图是某地气温日变化曲线图,则在这一天,该地的气温日较差是__11.5_℃__.
eq
\o(\s\up7(),\s\do5(第13题图))
eq
\o(\s\up7(),\s\do5(第14题图))
14.如图是某市某天的温度随时间变化的图象,通过观察可知这天__18__点时温度最高,9点时的温度是__28_℃__.
15.某城市大剧院地面的一部分为扇形,观众席的座位按下列方式设置:
排数
1
2
3
4
座位数
50
53
56
59
按这种方式排下去,第6排有__65__个座位.
16.(增城区校级期末)如图所示的是甲、乙两家商店销售同一种产品的销售价y(元)关于销售量x(件)的函数图象.给出下列说法,其中不正确的是__④__.
①售2件时,甲、乙两家的售价相同;
②买1件时,买乙家的合算;
③买3件时,买甲家的合算;
④乙家的1件售价约为3元.
17.★下面是用棋子摆成的“上”字型图案:
按照以上规律继续摆下去,那么通过观察,可以发现第n个“上”字需用__(4n+2)__枚棋子.
18.某市统计局统计了今年第一季度每月人均GDP的增长情况,并绘制了如图所示的统计图,下列结论:①1月份的人均GDP增长率最高;②2月份的人均GDP比1月份低;③这三个月的人均GDP都在增长.其中正确结论的序号是__①③__.
三、解答题(共66分)
19.(6分)某河受暴雨袭击,某天此河水的水位记录如下表:
时间(小时)
0
4
8
12
16
20
24
水位(米)
2
2.5
3
4
5
6
8
(1)上表反映了哪两个变量之间的关系?
(2)12时,水位是多高?
(3)哪一时段水位上升最快?
解:(1)由表可知,反映了时间和水位之间的关系.
(2)由表可以看出,12时,水位是4米.
(3)由表可以看出,在相等的时间间隔内,20时至24时水位上升最快.
20.(8分)某校办工厂现在年产值是15万元,计划以后每年增加2万元.
(1)写出年产值y(万元)与年数x之间的关系式;
(2)用表格表示当x从0变化到6(每次增加1)时,y的对应值;
(3)求5年后的年产值.
解:(1)关系式为y=2x+15.
(2)列表如下:
x
0
1
2
3
4
5
6
y=2x+15
15
17
19
21
23
25
27
(3)当x=5时,y=2×5+15=25,
∴5年后的年产值是25万元.
21.(8分)(张店区期末)某洗衣机在洗涤衣服时,经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量y(L)与时间x(min)之间的关系如折线图所示,根据图象解答下列问题:
(1)洗衣机的进水时间是________分钟,清洗时洗衣机中的水量是________升;
(2)进水时y与x之间的关系式是________;
(3)已知洗衣机的排水速度是每分钟18升,如果排水时间为2分钟,排水结束时洗衣机中剩下的水量是________升.
解:(1)4,40.
(2)y=10x.
(3)排水结束时洗衣机中剩下的水量是
40-18×2=4(升).
故答案为4.
22.(8分)某药物研究单位试制成功一种新药,经测试,如果患者按规定剂量服用,那么服药后每毫升血液中含药量y(微克)与时间x(时)之间的关系如图所示,如果每毫升血液中的含药量不小于20微克,那么这种药物才能发挥作用,请根据题意回答下列问题:
(1)服药几分钟后,药物开始发挥作用?
(2)服药几小时后,每毫升血液中的含药量最大,最大值是多少微克?
(3)服药后,药物发挥作用的时间有多少小时?
解:(1)服药20分钟后,药物开始发挥作用.
(2)服药2小时后,每毫升血液中的含药量最大,最大值是80微克.
(3)药物发挥作用的时间有6小时.
23.(10分)某机动车出发前油箱内有油42
L.行驶若干小时后,途中在加油站加油若干升.油箱中剩余油量Q(L)与行驶时间t(h)之间的关系如图所示,根据图象回答下列问题.
(1)机动车行驶几小时后加油?
(2)中途加油__24L__;
(3)如果加油站距目的地还有240
km,车速为40
km/h,要到达目的地,油箱中的油是否够用?并说明理由.
解:(1)由图知,5
h后加油.
(3)油箱中的油够用.理由:因为机动车每小时耗油(42-12)÷5=6
L,
所以240÷40×6=36
L,正好到达.
24.(12分)(竞秀区期末)甲骑摩托车从A地去B地.乙开汽车从B地去A地.同时出发,匀速行驶.各自到达终点后停止.甲、乙两人间的距离s(km)与甲行驶的时间t(h)之间的关系如图所示.
(1)以下是点M,点N,点P所代表的实际意义,请将M,N,P填入对应的横线上:
①甲到达终点:__P__;
②甲乙两人相遇:__M__;
③乙到达终点:__N__;
(2)AB两地之间的路程为__240__km;
(3)求甲、乙各自的速度;
(4)甲出发几小时后甲、乙两人相距180
km.
解:(3)甲的速度:
240÷6=40(km/h),
乙的速度:
240÷2-40=80(km/h).
(4)①相遇之前:
(240-180)÷(40+80)=0.5(h);
②相遇之后:
3+(180-120)÷40=4.5(h).
综上所述,甲出发0.5
h或4.5
h后,甲、乙两人相距180
km.
25.(14分)一只蚂蚁在一个半圆形的花坛的周边寻找食物,如图①,蚂蚁从圆心O出发,按图中箭头所示的方向,依次匀速爬完线段OA,半圆弧AB,线段BO后,回到出发点.蚂蚁离出发点的距离s(蚂蚁所在位置与O点之间线段的长度)与时间t之间的图象如图②所示.
(1)请直接写出:花坛的半径是________米,a=________;
(2)当t≤2时,求s与t之间的关系式;
(3)若沿途只有一处有食物,蚂蚁在寻找到食物后停下来吃了2分钟,并知蚂蚁在吃食物的前后,始终保持爬行且爬行速度不变,请你求出:
①蚂蚁停下来吃食物的地方离出发点的距离;
②蚂蚁返回O点的时间.(注:圆周率π的值取3)
解:(1)由图可知,花坛的半径是4米,
蚂蚁的速度为4÷2=2(米/分),
a=(4+4π)÷2=(4+4×3)÷2=8.
故答案为:4;8.
(2)由图象,可知当t=0时,s=0;
当t=2时,s=4,
∴s=2t(t≤2).
(3)①∵沿途只有一处食物,
∴蚂蚁只能在BO段吃食物,11-8-2=1,
∴蚂蚁从B爬1分钟找到食物,
4-1×2=2(米),
∴蚂蚁停下来吃食物的地方距出发点2米;
②∵蚂蚁停下来吃食的地方距出发点2米,
2÷2=1(分钟),11+1=12(分钟),
∴蚂蚁返回O点的时间为12分钟.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
