2020-2021学年黑龙江省大庆市肇源县七年级上学期期末数学试卷(五四学制) (Word版 含解析)
文档属性
| 名称 | 2020-2021学年黑龙江省大庆市肇源县七年级上学期期末数学试卷(五四学制) (Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 846.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-19 05:46:48 | ||
图片预览



文档简介
2020-2021学年黑龙江省大庆市肇源县七年级第一学期期末数学试卷(五四学制)
一、选择题(共10小题).
1.下列计算中,结果是a5的是( )
A.a2+a3 B.a2?a3 C.a10÷a2 D.(a2)3
2.如图,下列推理错误的是( )
A.∵∠1=∠2,∴a∥b B.∵b∥c,∴∠2=∠4
C.∵a∥b,b∥c,∴a∥c D.∵∠2+∠3=180°,∴a∥c
3.变量x与y之间的关系是y=2x+1,当y=5时,自变量x的值是( )
A.13 B.5 C.2 D.3.5
4.花花不慎将一块三角形的玻璃打碎成了如图所示的四块(图中所标①、②、③、④),若要配块与原来大小一样的三角形玻璃,应该带( )
A.第①块 B.第②块 C.第③块 D.第④块
5.如图,点P是直线a外一点,A,B,C,D都在直线上,PB⊥α于B,下列线段最短的是( )
A.PA B.PC C.PB D.PD
6.如图,AB=AC,添加下列条件,不能使△ABE≌△ACD的是( )
A.∠B=∠C B.∠AEB=∠ADC C.AE=AD D.BE=DC
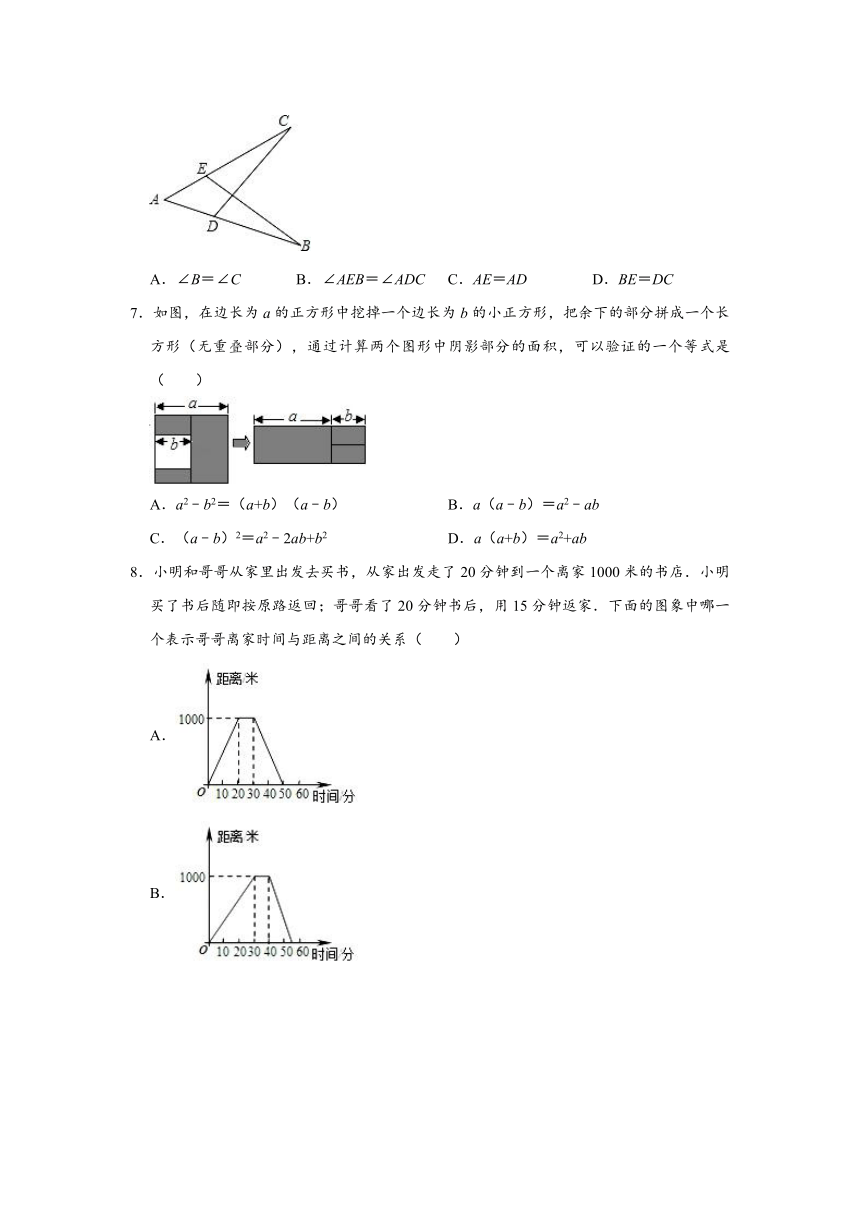
7.如图,在边长为a的正方形中挖掉一个边长为b的小正方形,把余下的部分拼成一个长方形(无重叠部分),通过计算两个图形中阴影部分的面积,可以验证的一个等式是( )
A.a2﹣b2=(a+b)(a﹣b) B.a(a﹣b)=a2﹣ab
C.(a﹣b)2=a2﹣2ab+b2 D.a(a+b)=a2+ab
8.小明和哥哥从家里出发去买书,从家出发走了20分钟到一个离家1000米的书店.小明买了书后随即按原路返回;哥哥看了20分钟书后,用15分钟返家.下面的图象中哪一个表示哥哥离家时间与距离之间的关系( )
A.
B.
C.
D.
9.如图,已知∠O,点P为其内一定点,分别在∠O的两边上找点A、B,使△PAB周长最小的是( )
A. B.
C. D.
10.如图,在△ABC中,∠BAC=90°,AB=AC=6cm,D为BC中点,E,F分别是AB,AC两边上的动点,且∠EDF=90°,下列结论:①BE=AF;②EF的长度不变;③∠BED+∠CFD的度数不变;④四边形AEDF的面积为9cm2.其中正确的结论个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题(共8小题).
11.某种秋冬流感病毒的直径约为0.000000308米,0.000000308用科学记数法表示为 .
12.已知a、b满足|a﹣1|+(b+3)2=0,则ab= .
13.若多项式a2+ka+25是完全平方式,则k的值是 .
14.用直尺和圆规作一个角等于已知角的示意图如下,则要说明∠D′O′C′=∠DOC,需要证明△D′O′C′≌△DOC,则这两个三角形全等的依据是 (写出全等的简写).
15.两条直线相交所构成的四个角,其中:①有三个角都相等;②有一对对顶角相等;③有一个角是直角;④有一对邻补角相等,能判定这两条直线垂直的有 .
16.如图,三角形ABC的高AD=4,BC=6,点E在BC上运动,若设BE的长为x,三角形ACE的面积为y,则y与x的关系式为 .
17.如图,三角形纸片ABC,AB=11cm,BC=7cm,AC=6cm,沿过点B的直线折叠这个三角形,使顶点C落在AB边上的点E处,折痕为BD,则△AED的周长为 cm.
18.如图,四边形ABCD中,∠BAD=∠C=90°,AB=AD,AE⊥BC,垂足为E,若线段AE=3,则四边形ABCD的面积是 .
三、计算题(本大题共4小题,19题4分,20-21题各5分,22题6分,共20分)
19.(4分)计算:(2x2)4﹣x?x3?x4.
20.(5分)计算:(﹣1)2020+(π﹣3.14)0﹣()﹣2﹣|1﹣|.
21.(5分)先化简,再求值:(a+3)2﹣(a+1)(a﹣1)﹣2(2a+4),其中a=.
22.(6分)利用乘法公式计算:20202﹣2019×2021.
四、解答题(本大题共6小题,23题6分,24题7分,25-27题各8分,28题9分,共46分)
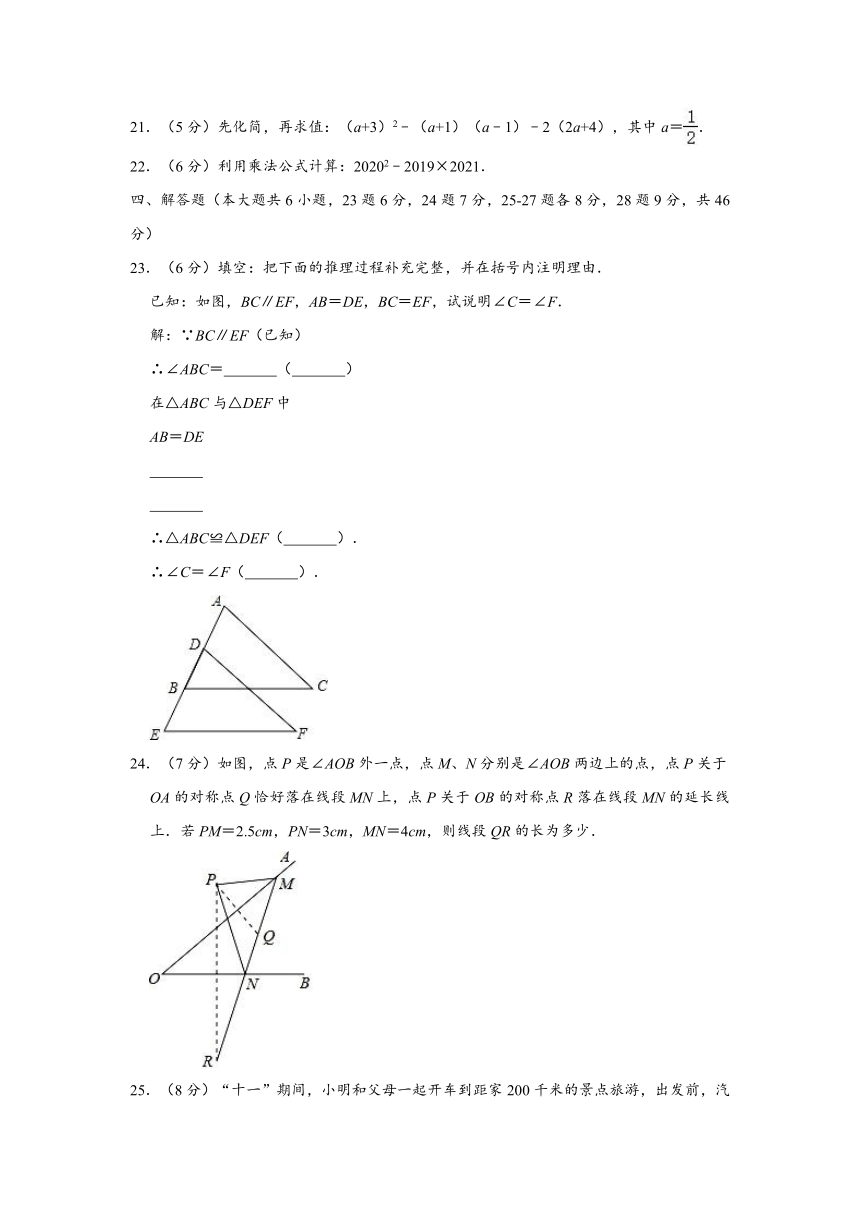
23.(6分)填空:把下面的推理过程补充完整,并在括号内注明理由.
已知:如图,BC∥EF,AB=DE,BC=EF,试说明∠C=∠F.
解:∵BC∥EF(已知)
∴∠ABC= ( )
在△ABC与△DEF中
AB=DE
∴△ABC≌△DEF( ).
∴∠C=∠F( ).
24.(7分)如图,点P是∠AOB外一点,点M、N分别是∠AOB两边上的点,点P关于OA的对称点Q恰好落在线段MN上,点P关于OB的对称点R落在线段MN的延长线上.若PM=2.5cm,PN=3cm,MN=4cm,则线段QR的长为多少.
25.(8分)“十一”期间,小明和父母一起开车到距家200千米的景点旅游,出发前,汽车油箱内储油45升,当行驶150千米时,发现油箱油箱余油量为30升(假设行驶过程中汽车的耗油量是均匀的).
(1)求该车平均每千米的耗油量,并写出行驶路程x(千米)与剩余油量Q(升)的关系式;
(2)当x=280(千米)时,求剩余油量Q的值;
(3)当油箱中剩余油量低于3升时,汽车将自动报警,如果往返途中不加油,他们能否在汽车报警前回到家?请说明理由.
26.(8分)如图,点A、C、D、B在同一条直线上,且AC=BD,∠A=∠B,∠E=∠F.
(1)求证:△ADE≌△BCF;
(2)若∠BCF=65°,求∠DMF的度数.
27.(8分)如图,在正方形网格上的一个△ABC,且每个小正方形的边长为1(其中点A,B,C均在网格上).
(1)作△ABC关于直线MN的轴对称图形△A′B′C′;
(2)在MN上画出点P,使得PA+PC最小;
(3)求出△ABC的面积.
28.(9分)如图,AC⊥BC,DC⊥EC,AC=BC,DC=EC,AE与BD交于点F.
(1)求证:AE=BD;
(2)求∠AFD的度数.
附加题(10分)
29.(10分)已知a+b=3,ab=2,求a2+b2,(a﹣b)2的值.
参考答案
一、选择题(共10小题).
1.下列计算中,结果是a5的是( )
A.a2+a3 B.a2?a3 C.a10÷a2 D.(a2)3
解:A、a2+a3,无法合并,故此选项不合题意;
B、a2?a3=a5,故此选项符合题意;
C、a10÷a2=a8,故此选项不合题意;
D、(a2)3=a6,故此选项不合题意.
故选:B.
2.如图,下列推理错误的是( )
A.∵∠1=∠2,∴a∥b B.∵b∥c,∴∠2=∠4
C.∵a∥b,b∥c,∴a∥c D.∵∠2+∠3=180°,∴a∥c
解:∵∠1=∠2,∴a∥b,选项A正确;
∵b∥c,∴∠2=∠4,选项B正确;
∵a∥b,b∥c,∴a∥c,选项C正确;
∵∠2+∠3=180°,∴b∥c,选项D错误;
故选:D.
3.变量x与y之间的关系是y=2x+1,当y=5时,自变量x的值是( )
A.13 B.5 C.2 D.3.5
解:当y=5时,5=2x+1,
解得:x=2,
故选:C.
4.花花不慎将一块三角形的玻璃打碎成了如图所示的四块(图中所标①、②、③、④),若要配块与原来大小一样的三角形玻璃,应该带( )
A.第①块 B.第②块 C.第③块 D.第④块
解:带②去可以利用“角边角”能配一块与原来大小一样的三角形玻璃.
故选:B.
5.如图,点P是直线a外一点,A,B,C,D都在直线上,PB⊥α于B,下列线段最短的是( )
A.PA B.PC C.PB D.PD
解:由题意,得
点P是直线a外一点,A,B,C,D都在直线上,PB⊥α于B,下列线段最短的是PB,
故选:C.
6.如图,AB=AC,添加下列条件,不能使△ABE≌△ACD的是( )
A.∠B=∠C B.∠AEB=∠ADC C.AE=AD D.BE=DC
解:A、添加∠B=∠C可利用ASA证明△ABE≌△ACD,故此选项不合题意;
B、添加∠AEB=∠ADC可利用AAS证明△ABE≌△ACD,故此选项不合题意;
C、添加AE=AD可利用SAS证明△ABE≌△ACD,故此选项不合题意;
D、添加EB=DC不能证明△ABE≌△ACD,故此选项符合题意;
故选:D.
7.如图,在边长为a的正方形中挖掉一个边长为b的小正方形,把余下的部分拼成一个长方形(无重叠部分),通过计算两个图形中阴影部分的面积,可以验证的一个等式是( )
A.a2﹣b2=(a+b)(a﹣b) B.a(a﹣b)=a2﹣ab
C.(a﹣b)2=a2﹣2ab+b2 D.a(a+b)=a2+ab
解:根据图形可知:第一个图形阴影部分的面积为a2﹣b2,第二个图形阴影部分的面积为(a+b)(a﹣b),
即a2﹣b2=(a+b)(a﹣b),
故选:A.
8.小明和哥哥从家里出发去买书,从家出发走了20分钟到一个离家1000米的书店.小明买了书后随即按原路返回;哥哥看了20分钟书后,用15分钟返家.下面的图象中哪一个表示哥哥离家时间与距离之间的关系( )
A.
B.
C.
D.
解:根据题意,从20分钟到40分钟哥哥在书店里看书,离家距离没有变化,是一条平行于x轴的线段.
故选:D.
9.如图,已知∠O,点P为其内一定点,分别在∠O的两边上找点A、B,使△PAB周长最小的是( )
A. B.
C. D.
解:分别在∠O的两边上找点A、B,使△PAB周长最小的是D选项,
故选:D.
10.如图,在△ABC中,∠BAC=90°,AB=AC=6cm,D为BC中点,E,F分别是AB,AC两边上的动点,且∠EDF=90°,下列结论:①BE=AF;②EF的长度不变;③∠BED+∠CFD的度数不变;④四边形AEDF的面积为9cm2.其中正确的结论个数是( )
A.1个 B.2个 C.3个 D.4个
解:∵AB=AC,∠BAC=90°,BD=CD,
∴AD⊥BC,AD=BD=DC,
∵∠BDA=∠EDF=90°,
∴∠BDE=∠ADF,
∵∠B=∠DAF=45°,
∴△BDE≌△ADF(ASA),
∴BE=AF,DE=DF,
故①正确,
∵DE=DF,∠EDF=90°,
∴△DEF是等腰直角三角形,
∵DE的长度是变化的,
∴EF的长度是变化的.
故②不正确.
∵△BDE≌△ADF,
∴∠BED=∠AFD,
∴∠BED+∠CFD=∠AFD+∠CFD=180°,
故③正确;
∵△BDE≌△ADF,
∴S△BDE=S△ADF,
∴S△ADE+S△ADF=S△ADE+S△BDE=S△ADB==×6×6=9(cm2).
故④正确.
故选:C.
二、填空题(本大题共8小题,共24分)
11.某种秋冬流感病毒的直径约为0.000000308米,0.000000308用科学记数法表示为 3.08×10﹣7 .
解:0.000000308表示成科学记数法为3.08×10﹣7,
故答案为:3.08×10﹣7.
12.已知a、b满足|a﹣1|+(b+3)2=0,则ab= 1 .
解:∵|a﹣1|+(b+3)2=0,
∴a﹣1=0,b+3=0,
∴a=1,b=﹣3,
∴ab=1﹣3=1.
故答案为:1.
13.若多项式a2+ka+25是完全平方式,则k的值是 ±10 .
解:∵a2+ka+25是完全平方式,
∴ka=±2×a×5,
∴k=±10,
故答案为:±10.
14.用直尺和圆规作一个角等于已知角的示意图如下,则要说明∠D′O′C′=∠DOC,需要证明△D′O′C′≌△DOC,则这两个三角形全等的依据是 SSS (写出全等的简写).
解:OC=O′C′,OD=O′D′,CD=C′D′,从而可以利用SSS判定其全等.
故填SSS.
15.两条直线相交所构成的四个角,其中:①有三个角都相等;②有一对对顶角相等;③有一个角是直角;④有一对邻补角相等,能判定这两条直线垂直的有 ①③④ .
解:两条直线相交所构成的四个角,
①因为有三个角都相等,都等于90°,所以能判定这两条直线垂直;
②因为有一对对顶角相等,但不一定等于90°,所以不能判定这两条直线垂直;
③有一个角是直角,能判定这两条直线垂直;
④因为一对邻补角相加等于180°,这对邻补角又相等都等于90°,所以能判定这两条直线垂直;
故答案为:①③④.
16.如图,三角形ABC的高AD=4,BC=6,点E在BC上运动,若设BE的长为x,三角形ACE的面积为y,则y与x的关系式为 y=﹣2x+12 .
解:由线段的和差,得CE=6﹣x,
由三角形的面积,得
y=×4×(6﹣x)
化简,得y=﹣2x+12,
故答案为:y=﹣2x+12.
17.如图,三角形纸片ABC,AB=11cm,BC=7cm,AC=6cm,沿过点B的直线折叠这个三角形,使顶点C落在AB边上的点E处,折痕为BD,则△AED的周长为 10 cm.
解:根据折叠可知:CD=DE、BE=BC,
∴AD+DE=AD+CD=AC=6cm,AE=AB﹣BE=AB﹣BC=4cm,
∴C△AED=AD+DE+AE=6+4=10cm.
故答案为:10.
18.如图,四边形ABCD中,∠BAD=∠C=90°,AB=AD,AE⊥BC,垂足为E,若线段AE=3,则四边形ABCD的面积是 9 .
解:过A点作AF⊥CD交CD的延长线于F点,如图,
∵AE⊥BC,AF⊥CF,
∴∠AEC=∠CFA=90°,
而∠C=90°,
∴四边形AECF为矩形,
∴∠2+∠3=90°,
又∵∠BAD=90°,
∴∠1=∠3,
在△ABE和△ADF中,
∵,
∴△ABE≌△ADF(AAS),
∴AE=AF=3,S△ABE=S△ADF,
∴四边形AECF是边长为3的正方形,
∴S四边形ABCD=S正方形AECF=32=9.
故答案为:9.
三、计算题(本大题共4小题,19题4分,20-21题各5分,22题6分,共20分)
19.(4分)计算:(2x2)4﹣x?x3?x4.
解:原式=16x8﹣x8
=15x8.
20.(5分)计算:(﹣1)2020+(π﹣3.14)0﹣()﹣2﹣|1﹣|.
解:(﹣1)2020+(π﹣3.14)0﹣()﹣2﹣|1﹣|
=1+1﹣9﹣+1
=﹣6﹣.
21.(5分)先化简,再求值:(a+3)2﹣(a+1)(a﹣1)﹣2(2a+4),其中a=.
解:原式=a2+6a+9﹣(a2﹣1)﹣4a﹣8
=2a+2,
∵a=,
∴原式=1+2=3.
22.(6分)利用乘法公式计算:20202﹣2019×2021.
解:20202﹣2019×2021
=20202﹣(2020﹣1)(2020+1)
=20202﹣(20202﹣1)
=1.
四、解答题(本大题共6小题,23题6分,24题7分,25-27题各8分,28题9分,共46分)
23.(6分)填空:把下面的推理过程补充完整,并在括号内注明理由.
已知:如图,BC∥EF,AB=DE,BC=EF,试说明∠C=∠F.
解:∵BC∥EF(已知)
∴∠ABC= ∠DEF ( 两直线平行,同位角相等 )
在△ABC与△DEF中
AB=DE
∠ABC=∠DEF
BC=EF
∴△ABC≌△DEF( SAS ).
∴∠C=∠F( 全等三角形的对应角相等 ).
解:∵BC∥EF(已知),
∴∠ABC=∠DEF(两直线平行,同位角相等),
在△ABC与△DEF中,
AB=DE,
∠ABC=∠E,
BC=EF,
∴△ABC≌△DEF(SAS),
∴∠C=∠F(全等三角形的对应角相等).
24.(7分)如图,点P是∠AOB外一点,点M、N分别是∠AOB两边上的点,点P关于OA的对称点Q恰好落在线段MN上,点P关于OB的对称点R落在线段MN的延长线上.若PM=2.5cm,PN=3cm,MN=4cm,则线段QR的长为多少.
解:QR=4.5cm,理由如下:
∵点P关于OA的对称点Q恰好落在线段MN上,点P关于OB的对称点R落在MN的延长线上,
∴PM=MQ,PN=NR.
∵PM=2.5cm,PN=3cm,MN=4cm,
∴RN=3cm,MQ=2.5cm,NQ=MN﹣MQ=4﹣2.5=1.5(cm).
∴QR=RN+NQ=3+1.5=4.5(cm).
25.(8分)“十一”期间,小明和父母一起开车到距家200千米的景点旅游,出发前,汽车油箱内储油45升,当行驶150千米时,发现油箱油箱余油量为30升(假设行驶过程中汽车的耗油量是均匀的).
(1)求该车平均每千米的耗油量,并写出行驶路程x(千米)与剩余油量Q(升)的关系式;
(2)当x=280(千米)时,求剩余油量Q的值;
(3)当油箱中剩余油量低于3升时,汽车将自动报警,如果往返途中不加油,他们能否在汽车报警前回到家?请说明理由.
解:(1)该车平均每千米的耗油量为(45﹣30)÷150=0.1(升/千米),
行驶路程x(千米)与剩余油量Q(升)的关系式为Q=45﹣0.1x;
(2)当x=280时,Q=45﹣0.1×280=17(L).
答:当x=280(千米)时,剩余油量Q的值为17L.
(3)(45﹣3)÷0.1=420(千米),
∵420>400,
∴他们能在汽车报警前回到家.
26.(8分)如图,点A、C、D、B在同一条直线上,且AC=BD,∠A=∠B,∠E=∠F.
(1)求证:△ADE≌△BCF;
(2)若∠BCF=65°,求∠DMF的度数.
【解答】证明:如图所示:
(1)∵AD=AC+CD,BC=BD+CD,AC=BD,
∴AD=BC,
在△AED和△BFC中,
,
∴△AED≌△BFC(AAS),
(2)∵△AED≌△BFC,
∴∠ADE=∠BCF,
又∵∠BCF=65°,
∴∠ADE=65°,
又∵∠ADE+∠BCF=∠DMF
∴∠DMF=65°×2=130°.
27.(8分)如图,在正方形网格上的一个△ABC,且每个小正方形的边长为1(其中点A,B,C均在网格上).
(1)作△ABC关于直线MN的轴对称图形△A′B′C′;
(2)在MN上画出点P,使得PA+PC最小;
(3)求出△ABC的面积.
解:(1)如图,△A′B′C′为所作;
(2)如图,点P为所作;
(3)△ABC的面积=3×4﹣×1×3﹣×3×2﹣×4×1=.
28.(9分)如图,AC⊥BC,DC⊥EC,AC=BC,DC=EC,AE与BD交于点F.
(1)求证:AE=BD;
(2)求∠AFD的度数.
解:(1)∵AC⊥BC,DC⊥EC,
∴∠ACB=∠DCE=90°,
∴∠ACE=∠BCD,
在△ACE和△BCD中,
,
∴△ACE≌△BCD(SAS),
∴AE=BD;
(2)设BC与AE交于点N,
∵∠ACB=90°,
∴∠A+∠ANC=90°,
∵△ACE≌△BCD,
∴∠A=∠B,
∵∠ANC=∠BNF,
∴∠B+∠BNF=∠A+∠ANC=90°,
∴∠AFD=∠B+∠BNF=90°.
一、选择题
29.(10分)已知a+b=3,ab=2,求a2+b2,(a﹣b)2的值.
解:∵a+b=3,
∴a2+2ab+b2=9,
∵ab=2,
∴a2+b2=9﹣2×2=5;
∴(a﹣b)2=a2﹣2ab+b2=5﹣2×2=1.
一、选择题(共10小题).
1.下列计算中,结果是a5的是( )
A.a2+a3 B.a2?a3 C.a10÷a2 D.(a2)3
2.如图,下列推理错误的是( )
A.∵∠1=∠2,∴a∥b B.∵b∥c,∴∠2=∠4
C.∵a∥b,b∥c,∴a∥c D.∵∠2+∠3=180°,∴a∥c
3.变量x与y之间的关系是y=2x+1,当y=5时,自变量x的值是( )
A.13 B.5 C.2 D.3.5
4.花花不慎将一块三角形的玻璃打碎成了如图所示的四块(图中所标①、②、③、④),若要配块与原来大小一样的三角形玻璃,应该带( )
A.第①块 B.第②块 C.第③块 D.第④块
5.如图,点P是直线a外一点,A,B,C,D都在直线上,PB⊥α于B,下列线段最短的是( )
A.PA B.PC C.PB D.PD
6.如图,AB=AC,添加下列条件,不能使△ABE≌△ACD的是( )
A.∠B=∠C B.∠AEB=∠ADC C.AE=AD D.BE=DC
7.如图,在边长为a的正方形中挖掉一个边长为b的小正方形,把余下的部分拼成一个长方形(无重叠部分),通过计算两个图形中阴影部分的面积,可以验证的一个等式是( )
A.a2﹣b2=(a+b)(a﹣b) B.a(a﹣b)=a2﹣ab
C.(a﹣b)2=a2﹣2ab+b2 D.a(a+b)=a2+ab
8.小明和哥哥从家里出发去买书,从家出发走了20分钟到一个离家1000米的书店.小明买了书后随即按原路返回;哥哥看了20分钟书后,用15分钟返家.下面的图象中哪一个表示哥哥离家时间与距离之间的关系( )
A.
B.
C.
D.
9.如图,已知∠O,点P为其内一定点,分别在∠O的两边上找点A、B,使△PAB周长最小的是( )
A. B.
C. D.
10.如图,在△ABC中,∠BAC=90°,AB=AC=6cm,D为BC中点,E,F分别是AB,AC两边上的动点,且∠EDF=90°,下列结论:①BE=AF;②EF的长度不变;③∠BED+∠CFD的度数不变;④四边形AEDF的面积为9cm2.其中正确的结论个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题(共8小题).
11.某种秋冬流感病毒的直径约为0.000000308米,0.000000308用科学记数法表示为 .
12.已知a、b满足|a﹣1|+(b+3)2=0,则ab= .
13.若多项式a2+ka+25是完全平方式,则k的值是 .
14.用直尺和圆规作一个角等于已知角的示意图如下,则要说明∠D′O′C′=∠DOC,需要证明△D′O′C′≌△DOC,则这两个三角形全等的依据是 (写出全等的简写).
15.两条直线相交所构成的四个角,其中:①有三个角都相等;②有一对对顶角相等;③有一个角是直角;④有一对邻补角相等,能判定这两条直线垂直的有 .
16.如图,三角形ABC的高AD=4,BC=6,点E在BC上运动,若设BE的长为x,三角形ACE的面积为y,则y与x的关系式为 .
17.如图,三角形纸片ABC,AB=11cm,BC=7cm,AC=6cm,沿过点B的直线折叠这个三角形,使顶点C落在AB边上的点E处,折痕为BD,则△AED的周长为 cm.
18.如图,四边形ABCD中,∠BAD=∠C=90°,AB=AD,AE⊥BC,垂足为E,若线段AE=3,则四边形ABCD的面积是 .
三、计算题(本大题共4小题,19题4分,20-21题各5分,22题6分,共20分)
19.(4分)计算:(2x2)4﹣x?x3?x4.
20.(5分)计算:(﹣1)2020+(π﹣3.14)0﹣()﹣2﹣|1﹣|.
21.(5分)先化简,再求值:(a+3)2﹣(a+1)(a﹣1)﹣2(2a+4),其中a=.
22.(6分)利用乘法公式计算:20202﹣2019×2021.
四、解答题(本大题共6小题,23题6分,24题7分,25-27题各8分,28题9分,共46分)
23.(6分)填空:把下面的推理过程补充完整,并在括号内注明理由.
已知:如图,BC∥EF,AB=DE,BC=EF,试说明∠C=∠F.
解:∵BC∥EF(已知)
∴∠ABC= ( )
在△ABC与△DEF中
AB=DE
∴△ABC≌△DEF( ).
∴∠C=∠F( ).
24.(7分)如图,点P是∠AOB外一点,点M、N分别是∠AOB两边上的点,点P关于OA的对称点Q恰好落在线段MN上,点P关于OB的对称点R落在线段MN的延长线上.若PM=2.5cm,PN=3cm,MN=4cm,则线段QR的长为多少.
25.(8分)“十一”期间,小明和父母一起开车到距家200千米的景点旅游,出发前,汽车油箱内储油45升,当行驶150千米时,发现油箱油箱余油量为30升(假设行驶过程中汽车的耗油量是均匀的).
(1)求该车平均每千米的耗油量,并写出行驶路程x(千米)与剩余油量Q(升)的关系式;
(2)当x=280(千米)时,求剩余油量Q的值;
(3)当油箱中剩余油量低于3升时,汽车将自动报警,如果往返途中不加油,他们能否在汽车报警前回到家?请说明理由.
26.(8分)如图,点A、C、D、B在同一条直线上,且AC=BD,∠A=∠B,∠E=∠F.
(1)求证:△ADE≌△BCF;
(2)若∠BCF=65°,求∠DMF的度数.
27.(8分)如图,在正方形网格上的一个△ABC,且每个小正方形的边长为1(其中点A,B,C均在网格上).
(1)作△ABC关于直线MN的轴对称图形△A′B′C′;
(2)在MN上画出点P,使得PA+PC最小;
(3)求出△ABC的面积.
28.(9分)如图,AC⊥BC,DC⊥EC,AC=BC,DC=EC,AE与BD交于点F.
(1)求证:AE=BD;
(2)求∠AFD的度数.
附加题(10分)
29.(10分)已知a+b=3,ab=2,求a2+b2,(a﹣b)2的值.
参考答案
一、选择题(共10小题).
1.下列计算中,结果是a5的是( )
A.a2+a3 B.a2?a3 C.a10÷a2 D.(a2)3
解:A、a2+a3,无法合并,故此选项不合题意;
B、a2?a3=a5,故此选项符合题意;
C、a10÷a2=a8,故此选项不合题意;
D、(a2)3=a6,故此选项不合题意.
故选:B.
2.如图,下列推理错误的是( )
A.∵∠1=∠2,∴a∥b B.∵b∥c,∴∠2=∠4
C.∵a∥b,b∥c,∴a∥c D.∵∠2+∠3=180°,∴a∥c
解:∵∠1=∠2,∴a∥b,选项A正确;
∵b∥c,∴∠2=∠4,选项B正确;
∵a∥b,b∥c,∴a∥c,选项C正确;
∵∠2+∠3=180°,∴b∥c,选项D错误;
故选:D.
3.变量x与y之间的关系是y=2x+1,当y=5时,自变量x的值是( )
A.13 B.5 C.2 D.3.5
解:当y=5时,5=2x+1,
解得:x=2,
故选:C.
4.花花不慎将一块三角形的玻璃打碎成了如图所示的四块(图中所标①、②、③、④),若要配块与原来大小一样的三角形玻璃,应该带( )
A.第①块 B.第②块 C.第③块 D.第④块
解:带②去可以利用“角边角”能配一块与原来大小一样的三角形玻璃.
故选:B.
5.如图,点P是直线a外一点,A,B,C,D都在直线上,PB⊥α于B,下列线段最短的是( )
A.PA B.PC C.PB D.PD
解:由题意,得
点P是直线a外一点,A,B,C,D都在直线上,PB⊥α于B,下列线段最短的是PB,
故选:C.
6.如图,AB=AC,添加下列条件,不能使△ABE≌△ACD的是( )
A.∠B=∠C B.∠AEB=∠ADC C.AE=AD D.BE=DC
解:A、添加∠B=∠C可利用ASA证明△ABE≌△ACD,故此选项不合题意;
B、添加∠AEB=∠ADC可利用AAS证明△ABE≌△ACD,故此选项不合题意;
C、添加AE=AD可利用SAS证明△ABE≌△ACD,故此选项不合题意;
D、添加EB=DC不能证明△ABE≌△ACD,故此选项符合题意;
故选:D.
7.如图,在边长为a的正方形中挖掉一个边长为b的小正方形,把余下的部分拼成一个长方形(无重叠部分),通过计算两个图形中阴影部分的面积,可以验证的一个等式是( )
A.a2﹣b2=(a+b)(a﹣b) B.a(a﹣b)=a2﹣ab
C.(a﹣b)2=a2﹣2ab+b2 D.a(a+b)=a2+ab
解:根据图形可知:第一个图形阴影部分的面积为a2﹣b2,第二个图形阴影部分的面积为(a+b)(a﹣b),
即a2﹣b2=(a+b)(a﹣b),
故选:A.
8.小明和哥哥从家里出发去买书,从家出发走了20分钟到一个离家1000米的书店.小明买了书后随即按原路返回;哥哥看了20分钟书后,用15分钟返家.下面的图象中哪一个表示哥哥离家时间与距离之间的关系( )
A.
B.
C.
D.
解:根据题意,从20分钟到40分钟哥哥在书店里看书,离家距离没有变化,是一条平行于x轴的线段.
故选:D.
9.如图,已知∠O,点P为其内一定点,分别在∠O的两边上找点A、B,使△PAB周长最小的是( )
A. B.
C. D.
解:分别在∠O的两边上找点A、B,使△PAB周长最小的是D选项,
故选:D.
10.如图,在△ABC中,∠BAC=90°,AB=AC=6cm,D为BC中点,E,F分别是AB,AC两边上的动点,且∠EDF=90°,下列结论:①BE=AF;②EF的长度不变;③∠BED+∠CFD的度数不变;④四边形AEDF的面积为9cm2.其中正确的结论个数是( )
A.1个 B.2个 C.3个 D.4个
解:∵AB=AC,∠BAC=90°,BD=CD,
∴AD⊥BC,AD=BD=DC,
∵∠BDA=∠EDF=90°,
∴∠BDE=∠ADF,
∵∠B=∠DAF=45°,
∴△BDE≌△ADF(ASA),
∴BE=AF,DE=DF,
故①正确,
∵DE=DF,∠EDF=90°,
∴△DEF是等腰直角三角形,
∵DE的长度是变化的,
∴EF的长度是变化的.
故②不正确.
∵△BDE≌△ADF,
∴∠BED=∠AFD,
∴∠BED+∠CFD=∠AFD+∠CFD=180°,
故③正确;
∵△BDE≌△ADF,
∴S△BDE=S△ADF,
∴S△ADE+S△ADF=S△ADE+S△BDE=S△ADB==×6×6=9(cm2).
故④正确.
故选:C.
二、填空题(本大题共8小题,共24分)
11.某种秋冬流感病毒的直径约为0.000000308米,0.000000308用科学记数法表示为 3.08×10﹣7 .
解:0.000000308表示成科学记数法为3.08×10﹣7,
故答案为:3.08×10﹣7.
12.已知a、b满足|a﹣1|+(b+3)2=0,则ab= 1 .
解:∵|a﹣1|+(b+3)2=0,
∴a﹣1=0,b+3=0,
∴a=1,b=﹣3,
∴ab=1﹣3=1.
故答案为:1.
13.若多项式a2+ka+25是完全平方式,则k的值是 ±10 .
解:∵a2+ka+25是完全平方式,
∴ka=±2×a×5,
∴k=±10,
故答案为:±10.
14.用直尺和圆规作一个角等于已知角的示意图如下,则要说明∠D′O′C′=∠DOC,需要证明△D′O′C′≌△DOC,则这两个三角形全等的依据是 SSS (写出全等的简写).
解:OC=O′C′,OD=O′D′,CD=C′D′,从而可以利用SSS判定其全等.
故填SSS.
15.两条直线相交所构成的四个角,其中:①有三个角都相等;②有一对对顶角相等;③有一个角是直角;④有一对邻补角相等,能判定这两条直线垂直的有 ①③④ .
解:两条直线相交所构成的四个角,
①因为有三个角都相等,都等于90°,所以能判定这两条直线垂直;
②因为有一对对顶角相等,但不一定等于90°,所以不能判定这两条直线垂直;
③有一个角是直角,能判定这两条直线垂直;
④因为一对邻补角相加等于180°,这对邻补角又相等都等于90°,所以能判定这两条直线垂直;
故答案为:①③④.
16.如图,三角形ABC的高AD=4,BC=6,点E在BC上运动,若设BE的长为x,三角形ACE的面积为y,则y与x的关系式为 y=﹣2x+12 .
解:由线段的和差,得CE=6﹣x,
由三角形的面积,得
y=×4×(6﹣x)
化简,得y=﹣2x+12,
故答案为:y=﹣2x+12.
17.如图,三角形纸片ABC,AB=11cm,BC=7cm,AC=6cm,沿过点B的直线折叠这个三角形,使顶点C落在AB边上的点E处,折痕为BD,则△AED的周长为 10 cm.
解:根据折叠可知:CD=DE、BE=BC,
∴AD+DE=AD+CD=AC=6cm,AE=AB﹣BE=AB﹣BC=4cm,
∴C△AED=AD+DE+AE=6+4=10cm.
故答案为:10.
18.如图,四边形ABCD中,∠BAD=∠C=90°,AB=AD,AE⊥BC,垂足为E,若线段AE=3,则四边形ABCD的面积是 9 .
解:过A点作AF⊥CD交CD的延长线于F点,如图,
∵AE⊥BC,AF⊥CF,
∴∠AEC=∠CFA=90°,
而∠C=90°,
∴四边形AECF为矩形,
∴∠2+∠3=90°,
又∵∠BAD=90°,
∴∠1=∠3,
在△ABE和△ADF中,
∵,
∴△ABE≌△ADF(AAS),
∴AE=AF=3,S△ABE=S△ADF,
∴四边形AECF是边长为3的正方形,
∴S四边形ABCD=S正方形AECF=32=9.
故答案为:9.
三、计算题(本大题共4小题,19题4分,20-21题各5分,22题6分,共20分)
19.(4分)计算:(2x2)4﹣x?x3?x4.
解:原式=16x8﹣x8
=15x8.
20.(5分)计算:(﹣1)2020+(π﹣3.14)0﹣()﹣2﹣|1﹣|.
解:(﹣1)2020+(π﹣3.14)0﹣()﹣2﹣|1﹣|
=1+1﹣9﹣+1
=﹣6﹣.
21.(5分)先化简,再求值:(a+3)2﹣(a+1)(a﹣1)﹣2(2a+4),其中a=.
解:原式=a2+6a+9﹣(a2﹣1)﹣4a﹣8
=2a+2,
∵a=,
∴原式=1+2=3.
22.(6分)利用乘法公式计算:20202﹣2019×2021.
解:20202﹣2019×2021
=20202﹣(2020﹣1)(2020+1)
=20202﹣(20202﹣1)
=1.
四、解答题(本大题共6小题,23题6分,24题7分,25-27题各8分,28题9分,共46分)
23.(6分)填空:把下面的推理过程补充完整,并在括号内注明理由.
已知:如图,BC∥EF,AB=DE,BC=EF,试说明∠C=∠F.
解:∵BC∥EF(已知)
∴∠ABC= ∠DEF ( 两直线平行,同位角相等 )
在△ABC与△DEF中
AB=DE
∠ABC=∠DEF
BC=EF
∴△ABC≌△DEF( SAS ).
∴∠C=∠F( 全等三角形的对应角相等 ).
解:∵BC∥EF(已知),
∴∠ABC=∠DEF(两直线平行,同位角相等),
在△ABC与△DEF中,
AB=DE,
∠ABC=∠E,
BC=EF,
∴△ABC≌△DEF(SAS),
∴∠C=∠F(全等三角形的对应角相等).
24.(7分)如图,点P是∠AOB外一点,点M、N分别是∠AOB两边上的点,点P关于OA的对称点Q恰好落在线段MN上,点P关于OB的对称点R落在线段MN的延长线上.若PM=2.5cm,PN=3cm,MN=4cm,则线段QR的长为多少.
解:QR=4.5cm,理由如下:
∵点P关于OA的对称点Q恰好落在线段MN上,点P关于OB的对称点R落在MN的延长线上,
∴PM=MQ,PN=NR.
∵PM=2.5cm,PN=3cm,MN=4cm,
∴RN=3cm,MQ=2.5cm,NQ=MN﹣MQ=4﹣2.5=1.5(cm).
∴QR=RN+NQ=3+1.5=4.5(cm).
25.(8分)“十一”期间,小明和父母一起开车到距家200千米的景点旅游,出发前,汽车油箱内储油45升,当行驶150千米时,发现油箱油箱余油量为30升(假设行驶过程中汽车的耗油量是均匀的).
(1)求该车平均每千米的耗油量,并写出行驶路程x(千米)与剩余油量Q(升)的关系式;
(2)当x=280(千米)时,求剩余油量Q的值;
(3)当油箱中剩余油量低于3升时,汽车将自动报警,如果往返途中不加油,他们能否在汽车报警前回到家?请说明理由.
解:(1)该车平均每千米的耗油量为(45﹣30)÷150=0.1(升/千米),
行驶路程x(千米)与剩余油量Q(升)的关系式为Q=45﹣0.1x;
(2)当x=280时,Q=45﹣0.1×280=17(L).
答:当x=280(千米)时,剩余油量Q的值为17L.
(3)(45﹣3)÷0.1=420(千米),
∵420>400,
∴他们能在汽车报警前回到家.
26.(8分)如图,点A、C、D、B在同一条直线上,且AC=BD,∠A=∠B,∠E=∠F.
(1)求证:△ADE≌△BCF;
(2)若∠BCF=65°,求∠DMF的度数.
【解答】证明:如图所示:
(1)∵AD=AC+CD,BC=BD+CD,AC=BD,
∴AD=BC,
在△AED和△BFC中,
,
∴△AED≌△BFC(AAS),
(2)∵△AED≌△BFC,
∴∠ADE=∠BCF,
又∵∠BCF=65°,
∴∠ADE=65°,
又∵∠ADE+∠BCF=∠DMF
∴∠DMF=65°×2=130°.
27.(8分)如图,在正方形网格上的一个△ABC,且每个小正方形的边长为1(其中点A,B,C均在网格上).
(1)作△ABC关于直线MN的轴对称图形△A′B′C′;
(2)在MN上画出点P,使得PA+PC最小;
(3)求出△ABC的面积.
解:(1)如图,△A′B′C′为所作;
(2)如图,点P为所作;
(3)△ABC的面积=3×4﹣×1×3﹣×3×2﹣×4×1=.
28.(9分)如图,AC⊥BC,DC⊥EC,AC=BC,DC=EC,AE与BD交于点F.
(1)求证:AE=BD;
(2)求∠AFD的度数.
解:(1)∵AC⊥BC,DC⊥EC,
∴∠ACB=∠DCE=90°,
∴∠ACE=∠BCD,
在△ACE和△BCD中,
,
∴△ACE≌△BCD(SAS),
∴AE=BD;
(2)设BC与AE交于点N,
∵∠ACB=90°,
∴∠A+∠ANC=90°,
∵△ACE≌△BCD,
∴∠A=∠B,
∵∠ANC=∠BNF,
∴∠B+∠BNF=∠A+∠ANC=90°,
∴∠AFD=∠B+∠BNF=90°.
一、选择题
29.(10分)已知a+b=3,ab=2,求a2+b2,(a﹣b)2的值.
解:∵a+b=3,
∴a2+2ab+b2=9,
∵ab=2,
∴a2+b2=9﹣2×2=5;
∴(a﹣b)2=a2﹣2ab+b2=5﹣2×2=1.
同课章节目录
