北师大版 九年级下册 2.1二次函数 课件(共50张)
文档属性
| 名称 | 北师大版 九年级下册 2.1二次函数 课件(共50张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-19 07:59:12 | ||
图片预览










文档简介
二次函数
【重点导航】
通过本课学习,大家将掌握以下内容
二次函数的图像和性质
2.二次函数的三种表示形式
3.二次函数在给定区间上的最值问题
一、二次函数y=ax2+bx+c(a≠0)的图象和性质
(1)是一条抛物线;
(2)对称轴是: x=
(3)顶点坐标是:
(4)开口方向:
a>0时,开口向上;
a<0时,开口向下.
x
y
0
【课程精讲】
1)a>0时,在对称轴左侧(x< ),函
数是减函数;在对称轴右侧(x> ) ,函数是增函数 。
a<0时,在对称轴左侧(x< ),函数
是增函数 ;在对称轴右侧(x> ),函数是减函数。
2) a>0时,y min=
a<0时,y max=
二、二次函数的三种表示形式
二次函数开口方向、对称轴和顶点坐标。
(1)一般式:
(2)顶点式:
(3)交点式:
对称轴:
顶点坐标:
对称轴:
顶点坐标:
x = h
( h ,k )
对称轴:
顶点坐标:
与x轴两个交点为A (x1,0)、B (x2 ,0)
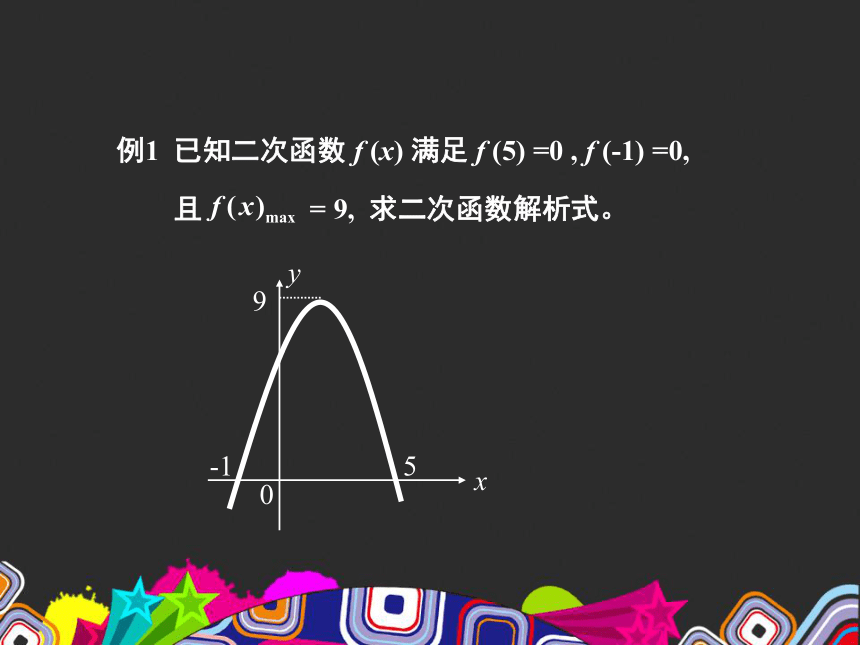
例1 已知二次函数 f (x) 满足 f (5) =0 , f (-1) =0,
且 = 9, 求二次函数解析式。
x
0
9
-1
5
y
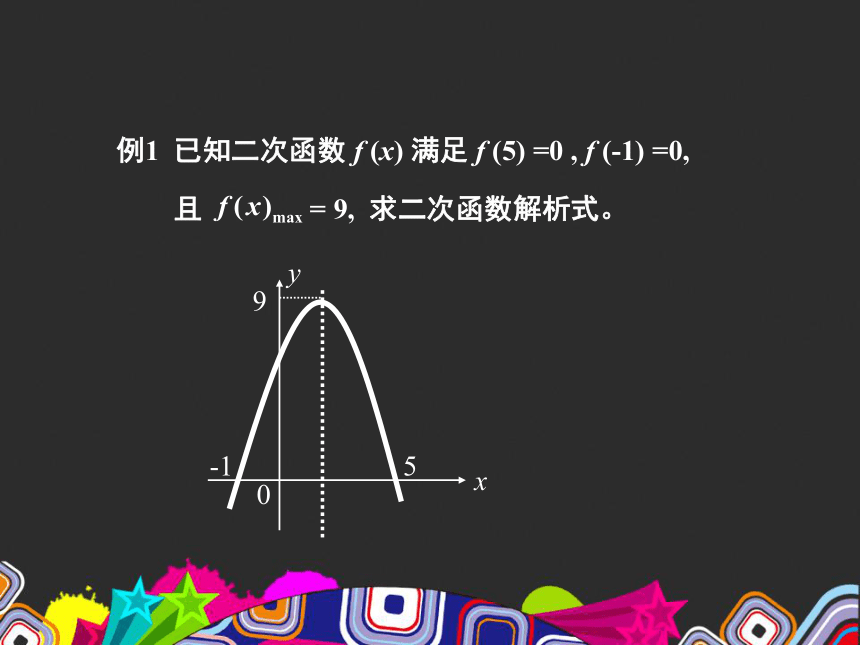
例1 已知二次函数 f (x) 满足 f (5) =0 , f (-1) =0,
且 = 9, 求二次函数解析式。
x
0
9
-1
5
y
例1 已知二次函数 f (x) 满足 f (5) =0 , f (-1) =0,
且 = 9, 求二次函数解析式。
例1 已知二次函数 f (x) 满足 f (5) =0 , f (-1) =0,
且 f (x)max= 9, 求二次函数解析式。
x
0
9
-1
5
y
例1 已知二次函数 f (x) 满足 f (5) =0 , f (-1) =0,
且 = 9, 求二次函数解析式。
例1 已知二次函数 f (x) 满足 f (5) =0 , f (-1) =0,
且 = 9, 求二次函数解析式。
练习: 已知二次函数 f (x) 满足
f (2) = -1 , f (-1) =-1, 且 = 8,
求其函数解析式。
练习: 已知二次函数 f (x) 满足
f (2) = -1 , f (-1) =-1, 且 = 8,
求其函数解析式。
练习: 已知二次函数 f (x) 满足
f (2) = -1 , f (-1) =-1, 且 = 8,
求其函数解析式。
x
0
8
-1
2
y
-1
三、二次函数在给定区间上的最值问题
例2 已知二次函数y=-x2+2x+3
(1)当x∈R, 求 f (x)的值域;
(2)当x∈[-1,0], 求 f (x)的值域;
(3)当x∈[0,3], 求 f (x)的值域;
(4)当x∈[a,a+2], 求 f (x)的最大值;
(1) x∈R, 求f (x) = -x2+2x+3的值域
解: 由题意得 f (x)= -(x-1)2 +4
∵对称轴x=1 ,a<0
∴抛物线开口向下
y max=f (1)=4
∴f (x)的值域为(-∞,4]
x
-1
0
4
3
y
(2)当x∈[-1,0], f (x) =-x2+2x+3的值域
解: 由题意得 f (x)= -(x-1)2 +4
∵f (x)在(-∞,1]上是增函数
∴f (x)在[-1,0]上是增函数
∴y min=f (-1)=0
y max=f (0)=3
∴ f (x)的值域为[0,3]
x
0
4
-1
3
y
1
(3)当x∈[0,3], 求f (x) =-x2+2x+3值域
解:由题意得 f (x)= -(x-1)2 +4
对称轴 x=1 , 而1∈[0,3]
∴ y max= f (1)=4
∵f (0)= 3,f (3)=0
∴f (x)的值域为[0,4]
x
0
4
-1
1
y
3
1.已知 f (x) = -x2-4x+5 ,求它在下列条件下的值域:
(1)当x∈[-1,2];
(2)当x∈[-3, -1];
(3)当x∈[-3,2].
思考练习:
f (x) = - (x-2)2 +9
f (x) = -(x+5) (x-1)
(1)当x∈[-1,2];
(2)当x∈[-3, -1];
(3)当x∈[-3,2].
x
0
9
-2
y
2
(1) y∈[-7,8]
-1
-3
(2) y∈[8,9]
(3) y∈[-7,9]
f (x) = -(x+2)2 +9
答
案
2.已知 f (x) = x2-4x-5 ,求它在下列条件下的值域:
(1)当x∈[-1, 0];
(2)当x∈[0, 3];
(3)当x∈[0,6];
(4)当x∈[4,6];
思考练习:
f (x) = (x-2)2 -1
f (x) = (x+1) (x-5)
(1)当x∈[-2, 0]; (4)当x∈[3,6];
解:f (x) = (x-2)2 -9
x
0
-9
-1
5
y
2
答案:
(1) [-5,7]
(4) [-8,7]
(2)当x∈[0, 3]; (3)当x∈[0,6];
解:f (x) = (x-2)2 -9
x
0
-9
-1
5
y
2
答案:
(2) [-9,-5]
(3) [-9,7]
三、二次函数在给定区间上的最值问题
例2 已知二次函数y=-x2+2x+3
(1)当x∈R, 求 f (x)的值域;
(2)当x∈[-1,0], 求 f (x)的值域;
(3)当x∈[0,3], 求 f (x)的值域;
(4)当x∈[a,a+2], 求 f (x)的最大值;
f (x)= -(x-1)2 +4
x
0
4
y
x=1
(4)当x∈[a,a+2], 求f (x) =-x2+2x+3最大值
x
-1
0
4
3
y
x
-1
0
4
3
y
x
-1
0
4
3
y
f (x) = -(x-1)2 +4 ,x∈[a,a+2],
解: 由题意得 f (x)= -(x-1)2 +4
①当a≤1≤a+2, 即-1≤a≤1时, y max= f(1)=4
②当a+2<1,即a<-1时,
∵f (x)在 (-∞,1]上是增函数
∴y max=f (a+2)= -a2-2a+3
③当a>1时,f (x)在 [1,+∞)是减函数
∴y max= f (a)=-a2+2a+3
变式训练:
把上题(4)改为求最小值
f (x) = -(x-1)2 +4 ,x [a,a+2]
x
-1
0
4
3
y
x
-1
0
4
3
y
对称轴为x=1,区间中点为 x=a+1
①当a+1≤1,即a≤0时,
y min = f (a)=-a2+2a+3
②当a+1>1,,即a>0时,
y min = f (a+2)=-a2-2a+3
解:f (x) = -(x-1)2 +4 ,x ∈[a,a+2],
总结:求二次函数f(x)=ax2+bx+c在[m,n]上
的最值或值域的一般方法是:
(1)配方,画草图,检查x0= 是否属于 [ m,n];
(2)当x0∈[m,n]时,f (m)、f (n)、f (x0)中的较大
者是最大值,较小者是最小值;
(3)当x0 [m,n]时,f(m)、f(n)中的较大者是最大
值, 较小者是最小值.
?
例3 求函数 y =x2+ax+3在区间[-1,1]上的最值
-1
1
0
y
x
例3 求函数 y =x2+ax+3在区间[-1,1]上的最值
-1
1
0
y
x
例3 求函数 y =x2+ax+3在区间[-1,1]上的最值
-1
1
0
y
x
-1
1
0
x
y
例3 求函数 y =x2+ax+3在区间[-1,1]上的最值
⑴当 即a≥ 2时
y min=f (-1)=4-a
函数在[-1,1]上是增函数
y max= f (1)=4+a
例3 求函数 y =x2+ax+3在区间[-1,1]上的最值
0
x
y
1
-1
0
x
y
1
-1
例3 求函数 y =x2+ax+3在区间[-1,1]上的最值
⑵
x
y
1
-1
例3 求函数 y =x2+ax+3在区间[-1,1]上的最值
0
(3)当 即a<-2时
y min= f (1)=4+a
y max= f (-1)=4-a
函数在[-1,1]上是减函数
例3 求函数 y =x2+ax+3在区间[-1,1]上的最值
0
x
y
1
-1
0
2
y
2
0
2
y
2
5
-1
【总结提升】
1.求二次函数在闭区间上最值的步骤是:
(1)配方;(2)画草图
比较对称轴和区间的相对位置关系
2.数形结合和分类讨论。
【重点导航】
通过本课学习,大家将掌握以下内容
二次函数的图像和性质
2.二次函数的三种表示形式
3.二次函数在给定区间上的最值问题
一、二次函数y=ax2+bx+c(a≠0)的图象和性质
(1)是一条抛物线;
(2)对称轴是: x=
(3)顶点坐标是:
(4)开口方向:
a>0时,开口向上;
a<0时,开口向下.
x
y
0
【课程精讲】
1)a>0时,在对称轴左侧(x< ),函
数是减函数;在对称轴右侧(x> ) ,函数是增函数 。
a<0时,在对称轴左侧(x< ),函数
是增函数 ;在对称轴右侧(x> ),函数是减函数。
2) a>0时,y min=
a<0时,y max=
二、二次函数的三种表示形式
二次函数开口方向、对称轴和顶点坐标。
(1)一般式:
(2)顶点式:
(3)交点式:
对称轴:
顶点坐标:
对称轴:
顶点坐标:
x = h
( h ,k )
对称轴:
顶点坐标:
与x轴两个交点为A (x1,0)、B (x2 ,0)
例1 已知二次函数 f (x) 满足 f (5) =0 , f (-1) =0,
且 = 9, 求二次函数解析式。
x
0
9
-1
5
y
例1 已知二次函数 f (x) 满足 f (5) =0 , f (-1) =0,
且 = 9, 求二次函数解析式。
x
0
9
-1
5
y
例1 已知二次函数 f (x) 满足 f (5) =0 , f (-1) =0,
且 = 9, 求二次函数解析式。
例1 已知二次函数 f (x) 满足 f (5) =0 , f (-1) =0,
且 f (x)max= 9, 求二次函数解析式。
x
0
9
-1
5
y
例1 已知二次函数 f (x) 满足 f (5) =0 , f (-1) =0,
且 = 9, 求二次函数解析式。
例1 已知二次函数 f (x) 满足 f (5) =0 , f (-1) =0,
且 = 9, 求二次函数解析式。
练习: 已知二次函数 f (x) 满足
f (2) = -1 , f (-1) =-1, 且 = 8,
求其函数解析式。
练习: 已知二次函数 f (x) 满足
f (2) = -1 , f (-1) =-1, 且 = 8,
求其函数解析式。
练习: 已知二次函数 f (x) 满足
f (2) = -1 , f (-1) =-1, 且 = 8,
求其函数解析式。
x
0
8
-1
2
y
-1
三、二次函数在给定区间上的最值问题
例2 已知二次函数y=-x2+2x+3
(1)当x∈R, 求 f (x)的值域;
(2)当x∈[-1,0], 求 f (x)的值域;
(3)当x∈[0,3], 求 f (x)的值域;
(4)当x∈[a,a+2], 求 f (x)的最大值;
(1) x∈R, 求f (x) = -x2+2x+3的值域
解: 由题意得 f (x)= -(x-1)2 +4
∵对称轴x=1 ,a<0
∴抛物线开口向下
y max=f (1)=4
∴f (x)的值域为(-∞,4]
x
-1
0
4
3
y
(2)当x∈[-1,0], f (x) =-x2+2x+3的值域
解: 由题意得 f (x)= -(x-1)2 +4
∵f (x)在(-∞,1]上是增函数
∴f (x)在[-1,0]上是增函数
∴y min=f (-1)=0
y max=f (0)=3
∴ f (x)的值域为[0,3]
x
0
4
-1
3
y
1
(3)当x∈[0,3], 求f (x) =-x2+2x+3值域
解:由题意得 f (x)= -(x-1)2 +4
对称轴 x=1 , 而1∈[0,3]
∴ y max= f (1)=4
∵f (0)= 3,f (3)=0
∴f (x)的值域为[0,4]
x
0
4
-1
1
y
3
1.已知 f (x) = -x2-4x+5 ,求它在下列条件下的值域:
(1)当x∈[-1,2];
(2)当x∈[-3, -1];
(3)当x∈[-3,2].
思考练习:
f (x) = - (x-2)2 +9
f (x) = -(x+5) (x-1)
(1)当x∈[-1,2];
(2)当x∈[-3, -1];
(3)当x∈[-3,2].
x
0
9
-2
y
2
(1) y∈[-7,8]
-1
-3
(2) y∈[8,9]
(3) y∈[-7,9]
f (x) = -(x+2)2 +9
答
案
2.已知 f (x) = x2-4x-5 ,求它在下列条件下的值域:
(1)当x∈[-1, 0];
(2)当x∈[0, 3];
(3)当x∈[0,6];
(4)当x∈[4,6];
思考练习:
f (x) = (x-2)2 -1
f (x) = (x+1) (x-5)
(1)当x∈[-2, 0]; (4)当x∈[3,6];
解:f (x) = (x-2)2 -9
x
0
-9
-1
5
y
2
答案:
(1) [-5,7]
(4) [-8,7]
(2)当x∈[0, 3]; (3)当x∈[0,6];
解:f (x) = (x-2)2 -9
x
0
-9
-1
5
y
2
答案:
(2) [-9,-5]
(3) [-9,7]
三、二次函数在给定区间上的最值问题
例2 已知二次函数y=-x2+2x+3
(1)当x∈R, 求 f (x)的值域;
(2)当x∈[-1,0], 求 f (x)的值域;
(3)当x∈[0,3], 求 f (x)的值域;
(4)当x∈[a,a+2], 求 f (x)的最大值;
f (x)= -(x-1)2 +4
x
0
4
y
x=1
(4)当x∈[a,a+2], 求f (x) =-x2+2x+3最大值
x
-1
0
4
3
y
x
-1
0
4
3
y
x
-1
0
4
3
y
f (x) = -(x-1)2 +4 ,x∈[a,a+2],
解: 由题意得 f (x)= -(x-1)2 +4
①当a≤1≤a+2, 即-1≤a≤1时, y max= f(1)=4
②当a+2<1,即a<-1时,
∵f (x)在 (-∞,1]上是增函数
∴y max=f (a+2)= -a2-2a+3
③当a>1时,f (x)在 [1,+∞)是减函数
∴y max= f (a)=-a2+2a+3
变式训练:
把上题(4)改为求最小值
f (x) = -(x-1)2 +4 ,x [a,a+2]
x
-1
0
4
3
y
x
-1
0
4
3
y
对称轴为x=1,区间中点为 x=a+1
①当a+1≤1,即a≤0时,
y min = f (a)=-a2+2a+3
②当a+1>1,,即a>0时,
y min = f (a+2)=-a2-2a+3
解:f (x) = -(x-1)2 +4 ,x ∈[a,a+2],
总结:求二次函数f(x)=ax2+bx+c在[m,n]上
的最值或值域的一般方法是:
(1)配方,画草图,检查x0= 是否属于 [ m,n];
(2)当x0∈[m,n]时,f (m)、f (n)、f (x0)中的较大
者是最大值,较小者是最小值;
(3)当x0 [m,n]时,f(m)、f(n)中的较大者是最大
值, 较小者是最小值.
?
例3 求函数 y =x2+ax+3在区间[-1,1]上的最值
-1
1
0
y
x
例3 求函数 y =x2+ax+3在区间[-1,1]上的最值
-1
1
0
y
x
例3 求函数 y =x2+ax+3在区间[-1,1]上的最值
-1
1
0
y
x
-1
1
0
x
y
例3 求函数 y =x2+ax+3在区间[-1,1]上的最值
⑴当 即a≥ 2时
y min=f (-1)=4-a
函数在[-1,1]上是增函数
y max= f (1)=4+a
例3 求函数 y =x2+ax+3在区间[-1,1]上的最值
0
x
y
1
-1
0
x
y
1
-1
例3 求函数 y =x2+ax+3在区间[-1,1]上的最值
⑵
x
y
1
-1
例3 求函数 y =x2+ax+3在区间[-1,1]上的最值
0
(3)当 即a<-2时
y min= f (1)=4+a
y max= f (-1)=4-a
函数在[-1,1]上是减函数
例3 求函数 y =x2+ax+3在区间[-1,1]上的最值
0
x
y
1
-1
0
2
y
2
0
2
y
2
5
-1
【总结提升】
1.求二次函数在闭区间上最值的步骤是:
(1)配方;(2)画草图
比较对称轴和区间的相对位置关系
2.数形结合和分类讨论。
