北师大版八年级下册2.6一元一次不等式组 课件 (共53张PPT)
文档属性
| 名称 | 北师大版八年级下册2.6一元一次不等式组 课件 (共53张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-19 00:00:00 | ||
图片预览










文档简介
1、不等式-X>-2的解是( )
A. X>2 B. X>-2 C. X<2 D. X<-2
C
2、不等式( )的解
在数轴表示,如图所示:
A. X>-1 B. X<-1 C. X≤-1 D. X≥-1
-2 -1 0 1 2
D
温故知新
现有两根木条a和b,a长10 cm,b长3 cm.如果再找一根木条c,用这三根木条钉成一个三角形木框,那么对木条c的长度有什么要求?
解:设这根木条c的长度为Xcm.
类似于方程组的概念,你能说出一元一次不等式组的概念吗?
三角形的两边之和大于第三边,
两边之差小于第三边.
x<10+3
1
x>10-3
2
注意:
(1)每个不等式必须为一元一次不等式;
(2)不等式必须是只含有同一个未知数;
(3)一元一次不等式的数量至少是两个或者多个。
类似于方程组,把这两个或两个以上的一元一次不等式合起来,就组成一个一元一次不等式组。
下列各式中,哪些是一元一次不等式组?
√
×
√
×
×
×
如何解此不等式组呢?
分析
类比方程组的解,怎样确定
不等式组中X的取值范围呢?
不等式组中的各不等式解集的公共部分,
就是不等式组中X的取值范围
x<10+3
1
x>10-3
2
议一议: (用数轴来解释)
在① X>-1 ② X>-2 ③ X<-2 ④ X <-1
X≤2 X>-1 X <2 X >1
各个一元一次不等式组中,两个不等式里X的值,
有公共部分的是: ;
没有公共部分的是: .
-2 -1 0 1 2
-2 -1 0 1 2
-2 -1 0 1 2
②
④
①
③
-2 -1 0 1 2
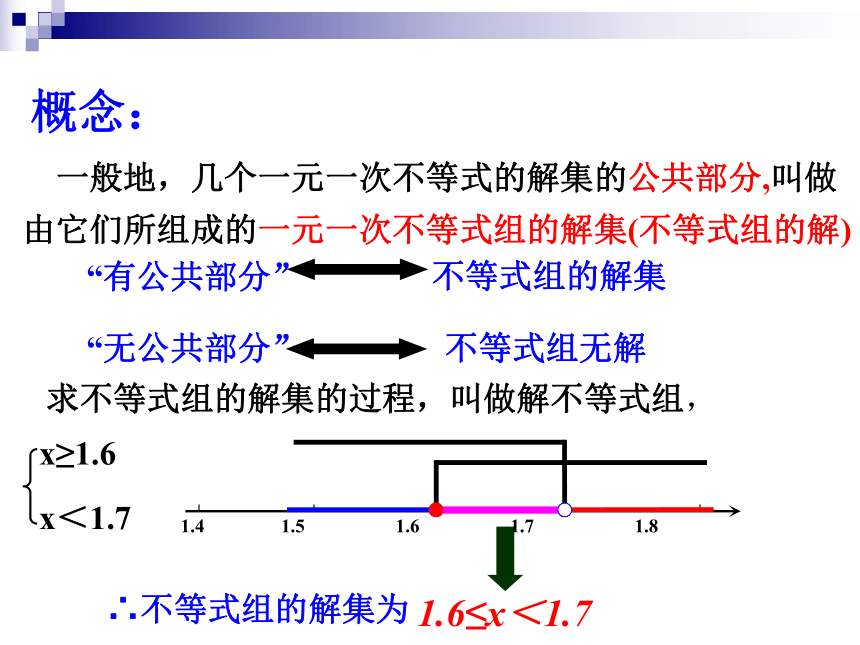
一般地,几个一元一次不等式的解集的公共部分,叫做由它们所组成的一元一次不等式组的解集(不等式组的解)
∴不等式组的解集为
1.6≤x<1.7
x<1.7
x≥1.6
1.4 1.5 1.6 1.7 1.8
“有公共部分”
不等式组的解集
“无公共部分”
不等式组无解
求不等式组的解集的过程,叫做解不等式组,
概念:
2
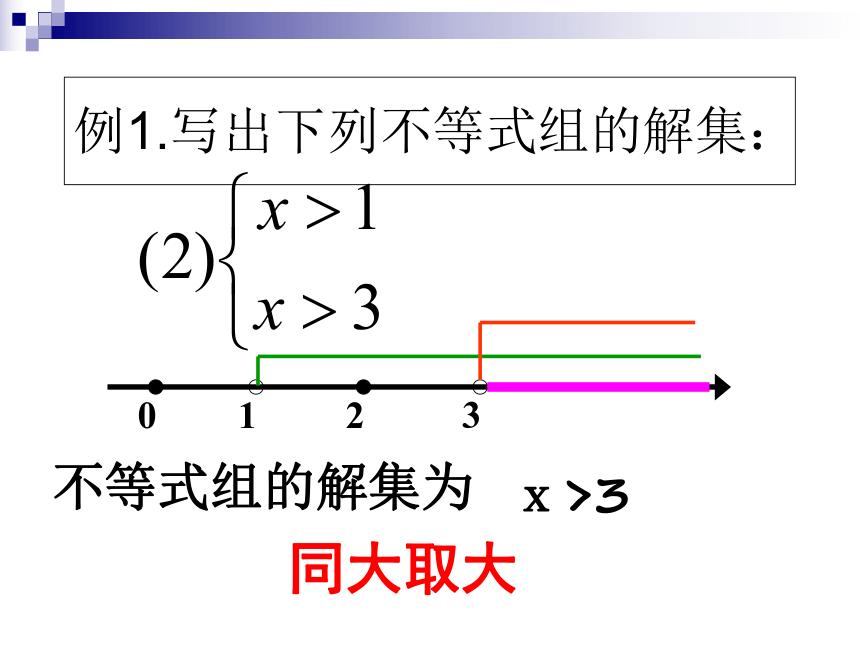
例1.写出下列不等式组的解集:
1
3
0
不等式组的解集为
x>3
同大取大
2
例2.利用数轴判断下列不等式组是否有解集?如有,请写出。
1
3
0
不等式组的解集为
x< 1
同小取小
2
例3.写出下列不等式组的解集:
1
3
0
不等式组的解集为
1<x< 3
大小小大中间找
2
例4.写出下列不等式组的解集:
1
3
0
不等式组的解集为空集
即:不等式组无解
大大小小解不了
练习1.求下列不等式组的解集:
比一比:看谁反应快
运用规律求下列不等式组的解集:
1. 同大取大,
2.同小取小;
3.大小小大中间找,
4.大大小小解不了。
x>2
x>-2
x<3
x<-4
3 -1 无解
无解
-2≤x<1
x≤-2
x<-2
a
a
a
b
x>a
x> b
x<a
x<b
x<a
x> b
x>a x<b
。
。
a
。
。
b
。
。
b
。
。
b
解集为 : x> b
(同大取大)
解集为 : x<a
(同小取小)
一元一次不等式组的解集的规律图析
(若当 a<b时 )
解集为: a<x<b
(大小小大中间找)
解集为:无解
(大大小小解不了)
0 2 3
例1:解下列不等式组
解: 由不等式①,移项得,
由不等式②,移项得,
把不等式①和 ②的解集在数轴上表示出来:
②
①
所以不等式组的解集:
议一议:
解一元一次不等式组的解题步骤:
(1)求出不等式组中各个不等式的解集;
(2)利用数轴,找出这些不等式解集的 公共部分;
(3)根据几个不等式解集的公共部分,写出 这个不等式组的解集。
根据上题的解答过程你认为解一元一次不等式组的一般步骤是什么?
0
8
②
①
解: 解不等式①,得,
解不等式②,得,
把不等式①和 ②的解集在数轴上表示出来:
这两个不等式的解集没有公共部分,所以不等式组无解。
例2:解下列不等式组
2x+1 < -1 ①
3-x≥1 ②
{
解不等式①得:
x< -1
解不等式②得:
x≤2
在数轴上表示不等式①、②的解集:
例3.解不等式组:
解:
1
0
2
-1
所以不等式组的解集为:
x< -1
①
②
解:解不等式①,得
解不等式②,得
不等式组的解集是
2
0
4
2.5
1
3
例4:解下列不等式组
解:
解不等式① ,得
解不等式② ,得
x < 1
x >-2
所以,原不等式组的解集是
- 2 < x<1
2 (x+2) < x+5
3 (x-2)+8 >2x
①
②
0
-2
1
-1
例5:解下列不等式组
0 m 1 3/2 2
例11.若不
等式组
有解,则m的取值范围是______。
解:化简不等式组得
根据不等式组解集的规律,得
因为不等式组有解,所以有
这中间的m当作数轴上的一个已知数
例12.已知关于x
不等式组
无解,则a的取值范围是____
解:将x>-1,x<2在数轴上表示出来为
要使不等式组无解,则a不能在-1的右边,则a≤-1
-1 2
C
B
A. ≥2
D. =2.
B. ≤2
C. 无解
(2)不等式组 的解集是( )
≥2
≤1
(1)不等式组 的解集是 ( )
x ≥-5
x> -2
A. ≥-5
D.
B. >-2
C. 无解
B
C
(4)如图: 则其解集是( )
-1
2.5
4
(3)不等式组 的解集在数轴表示为( )
≥ - 2
-5
-2
A.
-5
-2
C.
-5
-2
B.
D.
-5
-2
D
A.
B.
C.2.5< x ≤4
.
2.5
1
<
<
-
x
解一元一次不等式组的步骤:
2.利用数轴找几个解集的公共部分:
1.求出不等式组中各个不等式的解集;
3.写出这个不等式组的解集;
问题:我属兔,请你根据我的实际情况来猜测我的年龄?
提示: 属兔的年龄有可能是以下数据
5 17 29 41 53 ……
解:根据实际情况可知
20< 老师的年龄<40
又知老师属兔,所以老师的年龄是29岁。
例1、小宝和爸爸、妈妈三人在操场上玩跷跷板,爸爸体重为72千克,坐在跷跷板的一端,体重只有妈妈一半的小宝和妈妈一同坐在跷跷板的另一端,这时,爸爸的脚仍然着地。后来,小宝借来一副质量为6千克的哑铃,加在他和妈妈坐的一端,结果小宝和妈妈的脚着地。猜猜小宝的体重约有多少千克?
分析:从跷跷板的两种状况可以得到的关系
妈妈的体重+小宝的体重 爸爸的体重
妈妈的体重+小宝的体重+6千克 爸爸的体重
解:设小宝的体重是x千克,则妈妈的体重是2x千克。
由题意得
<
>
2x+x<72
2x+x+6>72
解得:22答:
例题解析2 如果每个学生分3个桃子,那么多8个;如果前面每人分5个,那么最后一个人分到桃子但少于3个.试问有几个学生,几个桃子?
设有x个学生,
整理得:
解得:
∵x表示人数
(3x+8)
(3x+8)-5(x-1) <3
2x<13
2x>10
x<6.5
x>5
即:5<x<6.5
∴ 3x+8=
解:
答:共有6个学生,26个桃子。
如果每个学生分3个桃子,那么多8个;如果前面每人分5个,那么最后一个人得到桃子但少于3个.试问有几个学生,几个桃子?
则有(3x+8)个桃子.
5(x-1)
>0
-
∴x取正整数
∴ x=6
26
列一元一次不等式组解应用题的一般步骤:
(1)审:审题,分析题目中已知什么,求什么,明确各数量之间的关系
(2)设:设适当的未知数
(3)找:找出题目中的所有不等关系
(4)列:列不等式组
(5)解、答:求出不等式组的解集,写出符合题意的答案
例3:某班有若干学生住宿,若每间住4人,则有20人没宿舍住;若每间住8人则有一间没有住满人,试求该班宿舍间数及住宿人数?
分析:第一个条件确定,可设有x间宿舍,则有4x+20个学生。有(x-1)间住了8人,住了8(x-1)人。最后一间为4x+20-8(x-1)人,不确定用不等式.
解:设有x间宿舍,则有4x+20人住宿,依题意可得
4x+20-8(x-1)>0
4x+20-8(x-1)<8
x<7
x>5
解得
因为宿舍是整数所以
x=6; 4x+20=44
答:该班有6间宿舍及44人住宿。
例4:一本英语书共98页,张力读了一周(7天)还没读完,而李永不到一周就已读完。李永平均每天比张力多读
3页,张力平均每天读多少页(答案取整数)?
解:设张力平均每天读x页
7( x +3)>98 ①
7 x <98 ②
解不等式①得 x >11
解不等式②得 x <14
因此,不等式组的解集为 11 < x<14
根据题意得,x的值应是整数,所以 x=12或13
答:张力平均每天读12或13页
例5.把价格为20元/千克的甲种糖果8千克和价格为18元/千克的乙种糖果若干千克混合,要使总价不超过400元,且糖果不少于15千克,所混合的乙种糖果最少是多少?
解:设所混合的乙种糖果有xkg.根据题意,得
解得
答:乙种糖果最少7千克.
例6、已知某工厂现有70米,52米的两种布料。现计划用这两种布料生产A、B两种型号的时装共80套,已知做一套A、B型号的时装所需的布料如下表所示,利用现有原料,工厂能否完成任务?若能,有几种生产方案?请你设计出来。
70米
52米
A
0.6米
0.9米
B
1.1米
0.4米
能不能完成啊,我要向厂长交代呀
讨论:1、完成任务是什么意思?
2、70米与52米是否一定要用完?
3、应该设什么为x?
4、用那些关系来列不等式组?
70米
52米
A
0.6米
0.9米
B
1.1米
0.4米
分析:若设生产A型号时装为x套,则生产B型号时装为(80-x)套
X套A型时装需要70米布料 +(80-x)套 B型时装需要的70米布料 70
X套A型时装需要52 米布料+(80-x)套 B型时装需要的52米布料 52
≤
≤
0.6x + 1.1(80-x ) ≤70
0.9x+0.4(80-x)≤52
解得:36 x 40
有五种方案:
36套A型和44套B型 37套A型和43套B型
38套A型和42套B型 39套A型和41套B型
40套A型和40套B型
列一元一次不等式(组)解决实际问题的步骤是:
实际问题
列不等式(组)
检验解是否符合实际
找出题中所有数量关系
解不等式(组)
设未知数
1、不等式组 的解集是( )
A.x ≥2,
D.x =2.
B.x≤2,
C. 无解,
2、不等式组 的整数解是( )
≤1
D. x≤1.
A. 0, 1 ,
B. 0 ,
C. 1,
D
C
≥2
≤2
D.不能确定.
A. -2, 0, -1 ,
B. -2
C. -2, -1,
3、不等式组 的负整数解是( )
≥-2,
4、不等式组 的解集在数轴上
表示为 ( )
≥-2,
A.
D.
C.
B.
C
B
-5
-2
-5
-2
-5
-2
-5
-2
-2
3
0
5、利用数轴判断下列不等式组是否有解集?如有,请写出。
(1)
(2)
(3)
(4)
-2
3
0
不等式组的解集是X>3
不等式组的解集是X< -2
-2
3
0
-2
3
0
不等式的解集是-2 无解
6、关于x的不等式组
有解,那么m的取值范围是( )
A、m>8 B、m≥8 C、m<8 D、m≤8
7、 如果
不等式组
的解集是x>a,则
a > b。
C
8.已知关于x
不等式组
无解,则a的取值范围是___
9.若不等式组
无解,则m的取值范围是__________。
10、关于x的
不等式组
的解集为x>3,则a的取值范围是( )。
A、a≥-3 B、a≤-3 C、a>-3 D、a<-3
A
m ≥2.5
a>3
A. X>2 B. X>-2 C. X<2 D. X<-2
C
2、不等式( )的解
在数轴表示,如图所示:
A. X>-1 B. X<-1 C. X≤-1 D. X≥-1
-2 -1 0 1 2
D
温故知新
现有两根木条a和b,a长10 cm,b长3 cm.如果再找一根木条c,用这三根木条钉成一个三角形木框,那么对木条c的长度有什么要求?
解:设这根木条c的长度为Xcm.
类似于方程组的概念,你能说出一元一次不等式组的概念吗?
三角形的两边之和大于第三边,
两边之差小于第三边.
x<10+3
1
x>10-3
2
注意:
(1)每个不等式必须为一元一次不等式;
(2)不等式必须是只含有同一个未知数;
(3)一元一次不等式的数量至少是两个或者多个。
类似于方程组,把这两个或两个以上的一元一次不等式合起来,就组成一个一元一次不等式组。
下列各式中,哪些是一元一次不等式组?
√
×
√
×
×
×
如何解此不等式组呢?
分析
类比方程组的解,怎样确定
不等式组中X的取值范围呢?
不等式组中的各不等式解集的公共部分,
就是不等式组中X的取值范围
x<10+3
1
x>10-3
2
议一议: (用数轴来解释)
在① X>-1 ② X>-2 ③ X<-2 ④ X <-1
X≤2 X>-1 X <2 X >1
各个一元一次不等式组中,两个不等式里X的值,
有公共部分的是: ;
没有公共部分的是: .
-2 -1 0 1 2
-2 -1 0 1 2
-2 -1 0 1 2
②
④
①
③
-2 -1 0 1 2
一般地,几个一元一次不等式的解集的公共部分,叫做由它们所组成的一元一次不等式组的解集(不等式组的解)
∴不等式组的解集为
1.6≤x<1.7
x<1.7
x≥1.6
1.4 1.5 1.6 1.7 1.8
“有公共部分”
不等式组的解集
“无公共部分”
不等式组无解
求不等式组的解集的过程,叫做解不等式组,
概念:
2
例1.写出下列不等式组的解集:
1
3
0
不等式组的解集为
x>3
同大取大
2
例2.利用数轴判断下列不等式组是否有解集?如有,请写出。
1
3
0
不等式组的解集为
x< 1
同小取小
2
例3.写出下列不等式组的解集:
1
3
0
不等式组的解集为
1<x< 3
大小小大中间找
2
例4.写出下列不等式组的解集:
1
3
0
不等式组的解集为空集
即:不等式组无解
大大小小解不了
练习1.求下列不等式组的解集:
比一比:看谁反应快
运用规律求下列不等式组的解集:
1. 同大取大,
2.同小取小;
3.大小小大中间找,
4.大大小小解不了。
x>2
x>-2
x<3
x<-4
3
无解
-2≤x<1
x≤-2
x<-2
a
a
a
b
x>a
x> b
x<a
x<b
x<a
x> b
x>a x<b
。
。
a
。
。
b
。
。
b
。
。
b
解集为 : x> b
(同大取大)
解集为 : x<a
(同小取小)
一元一次不等式组的解集的规律图析
(若当 a<b时 )
解集为: a<x<b
(大小小大中间找)
解集为:无解
(大大小小解不了)
0 2 3
例1:解下列不等式组
解: 由不等式①,移项得,
由不等式②,移项得,
把不等式①和 ②的解集在数轴上表示出来:
②
①
所以不等式组的解集:
议一议:
解一元一次不等式组的解题步骤:
(1)求出不等式组中各个不等式的解集;
(2)利用数轴,找出这些不等式解集的 公共部分;
(3)根据几个不等式解集的公共部分,写出 这个不等式组的解集。
根据上题的解答过程你认为解一元一次不等式组的一般步骤是什么?
0
8
②
①
解: 解不等式①,得,
解不等式②,得,
把不等式①和 ②的解集在数轴上表示出来:
这两个不等式的解集没有公共部分,所以不等式组无解。
例2:解下列不等式组
2x+1 < -1 ①
3-x≥1 ②
{
解不等式①得:
x< -1
解不等式②得:
x≤2
在数轴上表示不等式①、②的解集:
例3.解不等式组:
解:
1
0
2
-1
所以不等式组的解集为:
x< -1
①
②
解:解不等式①,得
解不等式②,得
不等式组的解集是
2
0
4
2.5
1
3
例4:解下列不等式组
解:
解不等式① ,得
解不等式② ,得
x < 1
x >-2
所以,原不等式组的解集是
- 2 < x<1
2 (x+2) < x+5
3 (x-2)+8 >2x
①
②
0
-2
1
-1
例5:解下列不等式组
0 m 1 3/2 2
例11.若不
等式组
有解,则m的取值范围是______。
解:化简不等式组得
根据不等式组解集的规律,得
因为不等式组有解,所以有
这中间的m当作数轴上的一个已知数
例12.已知关于x
不等式组
无解,则a的取值范围是____
解:将x>-1,x<2在数轴上表示出来为
要使不等式组无解,则a不能在-1的右边,则a≤-1
-1 2
C
B
A. ≥2
D. =2.
B. ≤2
C. 无解
(2)不等式组 的解集是( )
≥2
≤1
(1)不等式组 的解集是 ( )
x ≥-5
x> -2
A. ≥-5
D.
B. >-2
C. 无解
B
C
(4)如图: 则其解集是( )
-1
2.5
4
(3)不等式组 的解集在数轴表示为( )
≥ - 2
-5
-2
A.
-5
-2
C.
-5
-2
B.
D.
-5
-2
D
A.
B.
C.2.5< x ≤4
.
2.5
1
<
<
-
x
解一元一次不等式组的步骤:
2.利用数轴找几个解集的公共部分:
1.求出不等式组中各个不等式的解集;
3.写出这个不等式组的解集;
问题:我属兔,请你根据我的实际情况来猜测我的年龄?
提示: 属兔的年龄有可能是以下数据
5 17 29 41 53 ……
解:根据实际情况可知
20< 老师的年龄<40
又知老师属兔,所以老师的年龄是29岁。
例1、小宝和爸爸、妈妈三人在操场上玩跷跷板,爸爸体重为72千克,坐在跷跷板的一端,体重只有妈妈一半的小宝和妈妈一同坐在跷跷板的另一端,这时,爸爸的脚仍然着地。后来,小宝借来一副质量为6千克的哑铃,加在他和妈妈坐的一端,结果小宝和妈妈的脚着地。猜猜小宝的体重约有多少千克?
分析:从跷跷板的两种状况可以得到的关系
妈妈的体重+小宝的体重 爸爸的体重
妈妈的体重+小宝的体重+6千克 爸爸的体重
解:设小宝的体重是x千克,则妈妈的体重是2x千克。
由题意得
<
>
2x+x<72
2x+x+6>72
解得:22
例题解析2 如果每个学生分3个桃子,那么多8个;如果前面每人分5个,那么最后一个人分到桃子但少于3个.试问有几个学生,几个桃子?
设有x个学生,
整理得:
解得:
∵x表示人数
(3x+8)
(3x+8)-5(x-1) <3
2x<13
2x>10
x<6.5
x>5
即:5<x<6.5
∴ 3x+8=
解:
答:共有6个学生,26个桃子。
如果每个学生分3个桃子,那么多8个;如果前面每人分5个,那么最后一个人得到桃子但少于3个.试问有几个学生,几个桃子?
则有(3x+8)个桃子.
5(x-1)
>0
-
∴x取正整数
∴ x=6
26
列一元一次不等式组解应用题的一般步骤:
(1)审:审题,分析题目中已知什么,求什么,明确各数量之间的关系
(2)设:设适当的未知数
(3)找:找出题目中的所有不等关系
(4)列:列不等式组
(5)解、答:求出不等式组的解集,写出符合题意的答案
例3:某班有若干学生住宿,若每间住4人,则有20人没宿舍住;若每间住8人则有一间没有住满人,试求该班宿舍间数及住宿人数?
分析:第一个条件确定,可设有x间宿舍,则有4x+20个学生。有(x-1)间住了8人,住了8(x-1)人。最后一间为4x+20-8(x-1)人,不确定用不等式.
解:设有x间宿舍,则有4x+20人住宿,依题意可得
4x+20-8(x-1)>0
4x+20-8(x-1)<8
x<7
x>5
解得
因为宿舍是整数所以
x=6; 4x+20=44
答:该班有6间宿舍及44人住宿。
例4:一本英语书共98页,张力读了一周(7天)还没读完,而李永不到一周就已读完。李永平均每天比张力多读
3页,张力平均每天读多少页(答案取整数)?
解:设张力平均每天读x页
7( x +3)>98 ①
7 x <98 ②
解不等式①得 x >11
解不等式②得 x <14
因此,不等式组的解集为 11 < x<14
根据题意得,x的值应是整数,所以 x=12或13
答:张力平均每天读12或13页
例5.把价格为20元/千克的甲种糖果8千克和价格为18元/千克的乙种糖果若干千克混合,要使总价不超过400元,且糖果不少于15千克,所混合的乙种糖果最少是多少?
解:设所混合的乙种糖果有xkg.根据题意,得
解得
答:乙种糖果最少7千克.
例6、已知某工厂现有70米,52米的两种布料。现计划用这两种布料生产A、B两种型号的时装共80套,已知做一套A、B型号的时装所需的布料如下表所示,利用现有原料,工厂能否完成任务?若能,有几种生产方案?请你设计出来。
70米
52米
A
0.6米
0.9米
B
1.1米
0.4米
能不能完成啊,我要向厂长交代呀
讨论:1、完成任务是什么意思?
2、70米与52米是否一定要用完?
3、应该设什么为x?
4、用那些关系来列不等式组?
70米
52米
A
0.6米
0.9米
B
1.1米
0.4米
分析:若设生产A型号时装为x套,则生产B型号时装为(80-x)套
X套A型时装需要70米布料 +(80-x)套 B型时装需要的70米布料 70
X套A型时装需要52 米布料+(80-x)套 B型时装需要的52米布料 52
≤
≤
0.6x + 1.1(80-x ) ≤70
0.9x+0.4(80-x)≤52
解得:36 x 40
有五种方案:
36套A型和44套B型 37套A型和43套B型
38套A型和42套B型 39套A型和41套B型
40套A型和40套B型
列一元一次不等式(组)解决实际问题的步骤是:
实际问题
列不等式(组)
检验解是否符合实际
找出题中所有数量关系
解不等式(组)
设未知数
1、不等式组 的解集是( )
A.x ≥2,
D.x =2.
B.x≤2,
C. 无解,
2、不等式组 的整数解是( )
≤1
D. x≤1.
A. 0, 1 ,
B. 0 ,
C. 1,
D
C
≥2
≤2
D.不能确定.
A. -2, 0, -1 ,
B. -2
C. -2, -1,
3、不等式组 的负整数解是( )
≥-2,
4、不等式组 的解集在数轴上
表示为 ( )
≥-2,
A.
D.
C.
B.
C
B
-5
-2
-5
-2
-5
-2
-5
-2
-2
3
0
5、利用数轴判断下列不等式组是否有解集?如有,请写出。
(1)
(2)
(3)
(4)
-2
3
0
不等式组的解集是X>3
不等式组的解集是X< -2
-2
3
0
-2
3
0
不等式的解集是-2
6、关于x的不等式组
有解,那么m的取值范围是( )
A、m>8 B、m≥8 C、m<8 D、m≤8
7、 如果
不等式组
的解集是x>a,则
a > b。
C
8.已知关于x
不等式组
无解,则a的取值范围是___
9.若不等式组
无解,则m的取值范围是__________。
10、关于x的
不等式组
的解集为x>3,则a的取值范围是( )。
A、a≥-3 B、a≤-3 C、a>-3 D、a<-3
A
m ≥2.5
a>3
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
