北师大版八年级下册5.3分式的加减法 课件 (共30张PPT)
文档属性
| 名称 | 北师大版八年级下册5.3分式的加减法 课件 (共30张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 573.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-19 09:26:12 | ||
图片预览











文档简介
第五章 分式与分式方程
3 分式的加减法(一)
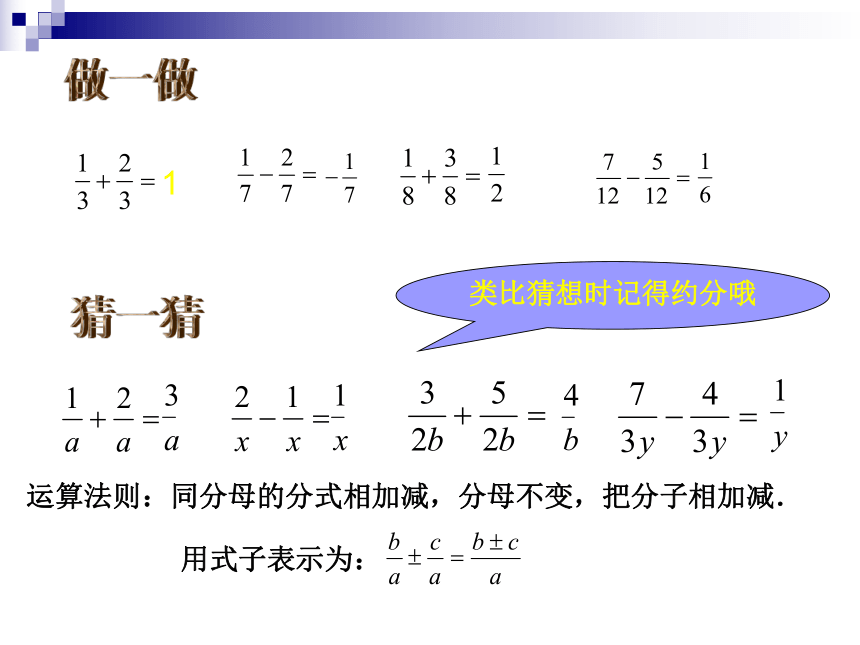
1
类比猜想时记得约分哦
运算法则:同分母的分式相加减,分母不变,把分子相加减.
用式子表示为:
解:原式
解:原式
解:原式
解:原式
记得给多项式的分子添括号,所得结果要化简哦!
答案:
例2 计算:
解:原式
解:原式
分母互为相反式时,改变一下运算符号即可变为同分母哦!
答案:
1、同分母分式加减法则是:同分母的分式相加
减。分母不变,把分子相加减。
2、学会用转化的思想将分母互为相反式的 分式
加减运算转化成同分母分式的加减法。
3、分子是多项式时,一定记得添括号后再进行
加减运算。
4、类比方法很多时候是对的哦,学会用这种方
法去分析和解决问题。
第五章 分式与分式方程
3 分式的加减法(二)
问题1:同分母分式是怎样进行加减运算的?
问题2:异分母分数又是如何进行加减呢?
问题3:那么 ?你是怎么做的?
同分母的分式相加减,分母不变,把分子相加减.
异分母分数相加减,先通分,化为同分母分
数后,再加减.
对于问题3,小明认为,只要把异分母的分式化
成同分母的分式,异分母的分式的加减问题就
变成了同分母的分式的加减问题。小亮同意小
明的这种看法,但他俩的具体做法不同:
你对这两种做法有何评论?与同伴交流。
小明:
小亮:
异分母的分式相加减,先通分,化为同分母的分
式,然后再按同分母分式的加减法法则进行计算.
例3:
解:
解:
解:原式
将下列各组分式通分:
2、计算:
小刚家和小丽家到学校的路程都是3km,其中小丽走的是平路,骑车速度2v km/h.小刚需要走1km 的上坡路、2km 的下坡路,在上坡路上的骑车速度为vkm/h,在下坡路上的骑车速度为3vkm/h.那么
(1)小刚从家到学校需要多长时间?
(2)小刚和小丽谁在路上花费的时间少?少用
多长时间?
:
答案(1)
(2)小丽花的时间 少,
比小刚少
1、异分母分式相加减的法则:
2、通分的关键就是找最简公分母,对于分母是
多项式且能够进行分解因式的要先分解后再
类比最小公倍数找最简公分母。
3、通分前是单项式的分子通分后就可能是多项
式了,运算时记得添括号。
4、运算结果要约分,有一些运算律仍然适用。
用两种方法计算:
解:法一(按运算顺序)
原式
法二(利用乘法分配律)
原式
第五章 分式与分式方程
3 分式的加减法(三)
同分母分式是怎样进行加减运算的?异分母分式呢?
同分母的分式相加减,分母不变,把分子相加减.
异分母的分式相加减,先通分,化为同分母的分
式,然后再按同分母分式的加减法法则进行计算.
练一练
答案:
例6
解:原式
解:原式
记得通分后分子添括号哦!
计算:
例6 已知
,求
的值.
解;原式
因为
即
所以,原式
还有其它接法吗?
先化简,再求值:
(1)已知
,求
的值.
,求
的值.
(2)已知
答案:
答案:
(2)实际修建这条盲道的工期比原计划缩短了几天?
(1)原计划修建这条盲道需少天?实际修建这条盲道用了
多少天?
解:(1)原计划修建需
天,
实际修建需
天;
(2)实比原计划缩短了
天.
根据规划设计,某工程队准备修建一条长 1 120 m 的盲道.由于采用新的施工方式,实际每天修建盲道的长度比原计划增加 10 m,从而缩短了工期.假设原计划每天修建盲道 x m,那么
某蓄水池装有 A,B 两个进水管,每小时可
分别进水 a t,b t.若单独开放 A 进水管,p h 可将该水池注满.如果 A,B 两根水管同时开放,那么能提前多长时间将该蓄水池注满?
答案: h .
1、异分母分式相加减的法则及通分的注意事项。
2、分式的化简求值及变形。
3、实际问题中能正确把握分式所表示的意义将
更有助于解题。
1、计算
2、甲,乙两地相距360km,新修的高速公路开通后,在甲,乙两地间行驶的长途客运车平均车速提高了50%而从甲地到乙地的时间缩短了2h,试确定原来的平均车速。
3、八年级(1)班学生周末坐车到风景区游览,风景区距学校100公里。一部分学生坐慢车先行,出发1小后,另一部分学生坐快车前往,结果快车比慢车还早到1小时。已知快车的速度是慢车速度的1.5倍,求慢车的速度。
3 分式的加减法(一)
1
类比猜想时记得约分哦
运算法则:同分母的分式相加减,分母不变,把分子相加减.
用式子表示为:
解:原式
解:原式
解:原式
解:原式
记得给多项式的分子添括号,所得结果要化简哦!
答案:
例2 计算:
解:原式
解:原式
分母互为相反式时,改变一下运算符号即可变为同分母哦!
答案:
1、同分母分式加减法则是:同分母的分式相加
减。分母不变,把分子相加减。
2、学会用转化的思想将分母互为相反式的 分式
加减运算转化成同分母分式的加减法。
3、分子是多项式时,一定记得添括号后再进行
加减运算。
4、类比方法很多时候是对的哦,学会用这种方
法去分析和解决问题。
第五章 分式与分式方程
3 分式的加减法(二)
问题1:同分母分式是怎样进行加减运算的?
问题2:异分母分数又是如何进行加减呢?
问题3:那么 ?你是怎么做的?
同分母的分式相加减,分母不变,把分子相加减.
异分母分数相加减,先通分,化为同分母分
数后,再加减.
对于问题3,小明认为,只要把异分母的分式化
成同分母的分式,异分母的分式的加减问题就
变成了同分母的分式的加减问题。小亮同意小
明的这种看法,但他俩的具体做法不同:
你对这两种做法有何评论?与同伴交流。
小明:
小亮:
异分母的分式相加减,先通分,化为同分母的分
式,然后再按同分母分式的加减法法则进行计算.
例3:
解:
解:
解:原式
将下列各组分式通分:
2、计算:
小刚家和小丽家到学校的路程都是3km,其中小丽走的是平路,骑车速度2v km/h.小刚需要走1km 的上坡路、2km 的下坡路,在上坡路上的骑车速度为vkm/h,在下坡路上的骑车速度为3vkm/h.那么
(1)小刚从家到学校需要多长时间?
(2)小刚和小丽谁在路上花费的时间少?少用
多长时间?
:
答案(1)
(2)小丽花的时间 少,
比小刚少
1、异分母分式相加减的法则:
2、通分的关键就是找最简公分母,对于分母是
多项式且能够进行分解因式的要先分解后再
类比最小公倍数找最简公分母。
3、通分前是单项式的分子通分后就可能是多项
式了,运算时记得添括号。
4、运算结果要约分,有一些运算律仍然适用。
用两种方法计算:
解:法一(按运算顺序)
原式
法二(利用乘法分配律)
原式
第五章 分式与分式方程
3 分式的加减法(三)
同分母分式是怎样进行加减运算的?异分母分式呢?
同分母的分式相加减,分母不变,把分子相加减.
异分母的分式相加减,先通分,化为同分母的分
式,然后再按同分母分式的加减法法则进行计算.
练一练
答案:
例6
解:原式
解:原式
记得通分后分子添括号哦!
计算:
例6 已知
,求
的值.
解;原式
因为
即
所以,原式
还有其它接法吗?
先化简,再求值:
(1)已知
,求
的值.
,求
的值.
(2)已知
答案:
答案:
(2)实际修建这条盲道的工期比原计划缩短了几天?
(1)原计划修建这条盲道需少天?实际修建这条盲道用了
多少天?
解:(1)原计划修建需
天,
实际修建需
天;
(2)实比原计划缩短了
天.
根据规划设计,某工程队准备修建一条长 1 120 m 的盲道.由于采用新的施工方式,实际每天修建盲道的长度比原计划增加 10 m,从而缩短了工期.假设原计划每天修建盲道 x m,那么
某蓄水池装有 A,B 两个进水管,每小时可
分别进水 a t,b t.若单独开放 A 进水管,p h 可将该水池注满.如果 A,B 两根水管同时开放,那么能提前多长时间将该蓄水池注满?
答案: h .
1、异分母分式相加减的法则及通分的注意事项。
2、分式的化简求值及变形。
3、实际问题中能正确把握分式所表示的意义将
更有助于解题。
1、计算
2、甲,乙两地相距360km,新修的高速公路开通后,在甲,乙两地间行驶的长途客运车平均车速提高了50%而从甲地到乙地的时间缩短了2h,试确定原来的平均车速。
3、八年级(1)班学生周末坐车到风景区游览,风景区距学校100公里。一部分学生坐慢车先行,出发1小后,另一部分学生坐快车前往,结果快车比慢车还早到1小时。已知快车的速度是慢车速度的1.5倍,求慢车的速度。
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
