北师大版九年级数学下册课件:第三章圆第二讲垂径定理、圆周角与圆心角的关系(共30张PPT)
文档属性
| 名称 | 北师大版九年级数学下册课件:第三章圆第二讲垂径定理、圆周角与圆心角的关系(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-19 00:00:00 | ||
图片预览








文档简介
第二节
教学内容
1.垂经定理
2.圆周角与圆心角的关系
圆
1.1垂径定理
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
例1如图,AB是⊙O的直径,弦CD⊥AB,垂足为M,下列结论不一定成立的是( )
A.CM=DM
B.
C.∠ACD=∠ADC
D.OM=MD
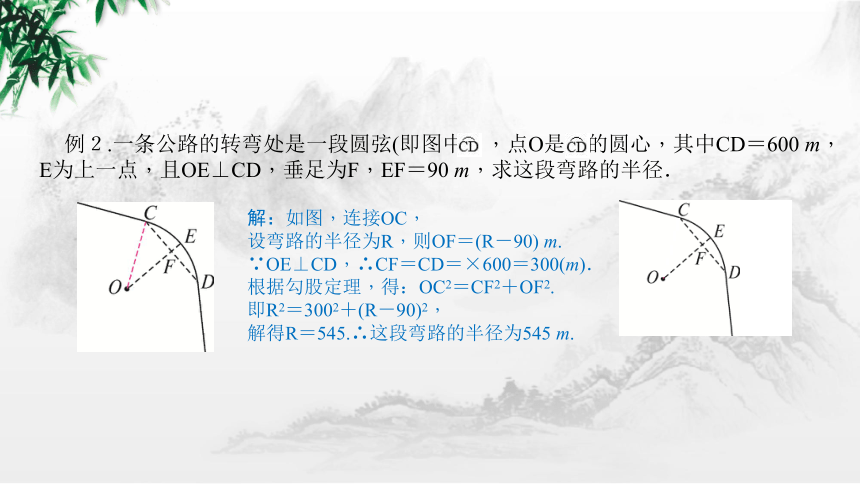
例2.一条公路的转弯处是一段圆弦(即图中 ,点O是 的圆心,其中CD=600 m,E为上一点,且OE⊥CD,垂足为F,EF=90 m,求这段弯路的半径.
解:如图,连接OC,
设弯路的半径为R,则OF=(R-90) m.
∵OE⊥CD,∴CF=CD=×600=300(m).
根据勾股定理,得:OC2=CF2+OF2.
即R2=3002+(R-90)2,
解得R=545.∴这段弯路的半径为545 m.
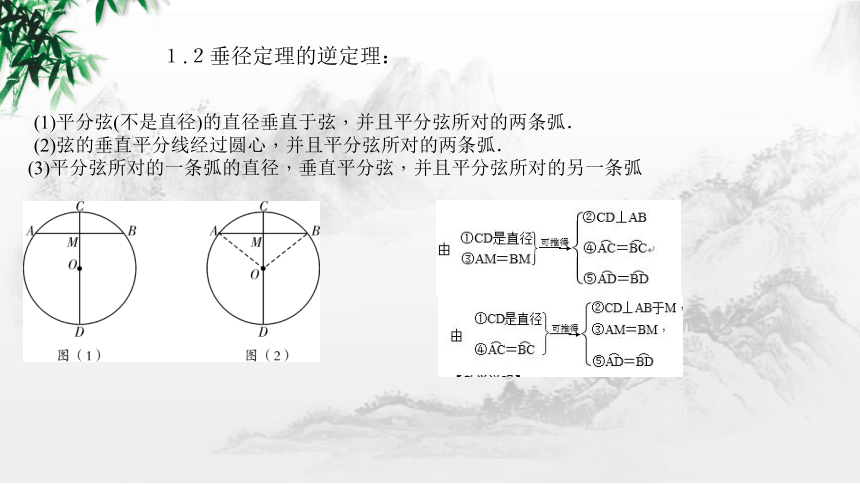
(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧.
(3)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧
1.2垂径定理的逆定理:
例3.OC交AB于点D,AD=DB,AB=6 cm,CD=1 cm,求⊙O的半径长.
解:设圆的半径为r,则OB=OC=r,
∴32+(r-1)2=r2,
解得r=5 cm.
即⊙O的半径长为5 cm.
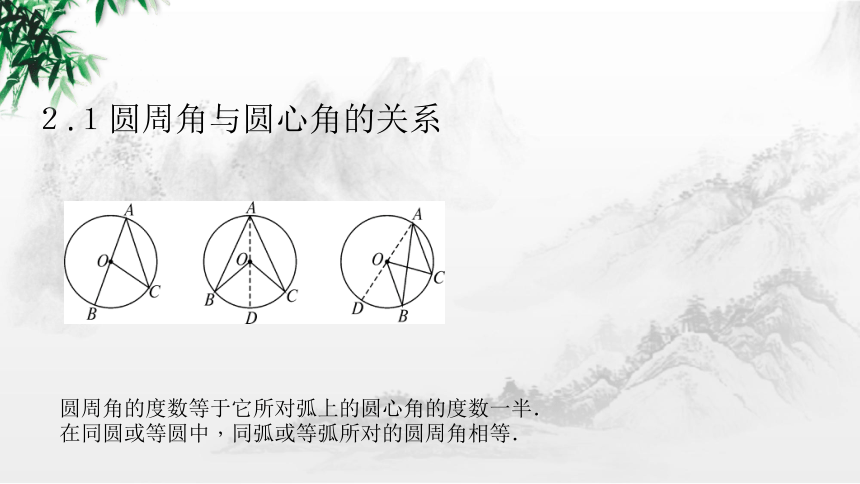
2.1圆周角与圆心角的关系
圆周角的度数等于它所对弧上的圆心角的度数一半.
在同圆或等圆中,同弧或等弧所对的圆周角相等.
2.1圆周角与圆心角的关系
例4已知BD是⊙O的直径,点A、C在⊙O上, ,∠AOB=60°,则∠BDC的度数是( )
A.20° B.25°
C.30° D.40°
解析:∵=,∠AOB=60°,
∴∠BDC=∠AOB=30°.
故选C.
例5.已知A,B,C在⊙O上,为优弧,下列选项中与∠AOB相等的是( )
A.2∠C B.4∠B
C.4∠A D.∠B+∠C
由圆周角定理可得:∠AOB=2∠C.
故选A.
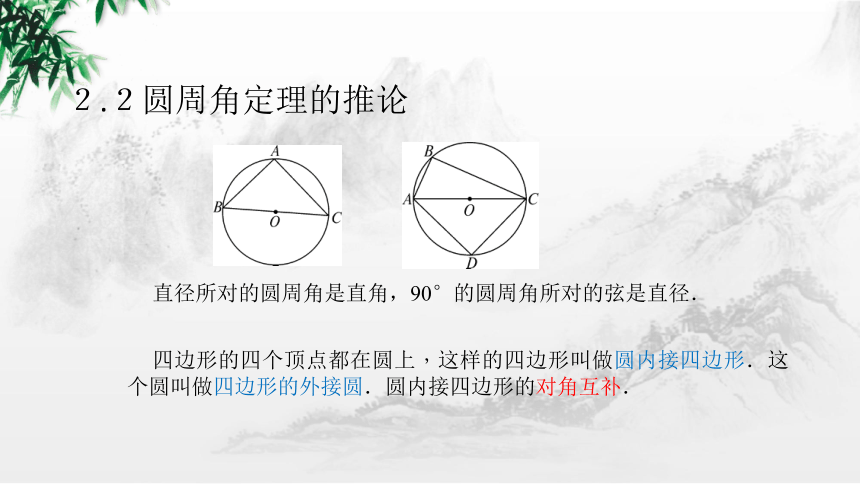
2.2圆周角定理的推论
直径所对的圆周角是直角,90°的圆周角所对的弦是直径.
四边形的四个顶点都在圆上,这样的四边形叫做圆内接四边形.这个圆叫做四边形的外接圆.圆内接四边形的对角互补.
例6.⊙O的两弦AD,BC相交于点E,连接AC,BD,AO,BO.若∠ACB=60°,则下列结论正确的是( )
A.∠AOB=60° B.∠ADB=60°
C.∠AEB=60° D.∠AEB=30°
解析:由圆周角定理及推论可知,
,∠ACB=∠ADB.
∵∠ACB=60°,
∴∠AOB=120°,∠ADB=60°.
答案:B
例7.△ABC为⊙O的内接三角形,若∠AOC=160°,则∠ABC的度数是( )
A.80° B.160° C.100° D.80°或100°
解析:当点B在优弧 上时,∠ABC=2∠AOC=×160°=80°.
当点B在劣弧 上时,∠AB′C=180°-∠ABC=180°-80°=100°.
所以∠ABC的度数是80°或100°.
答案:D
随堂练习:
1.AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OE∥AC交半圆O于点E,过点E作EF⊥AB于F.若AC=2,则OF的长为(?? )
??????????????????
C
2.边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则∠BED的正切值等于(??? )
3.已知点E在半径为5的⊙O上运动,AB是⊙O的弦且AB=8,则使△ABE的面积为8 的点E共有( ?????)个??
A.??? 1??????????????????????????????????????????B.?2??????????????????????????????????????????C.?3??????????????????????????????????????????D.?4
C
4.下列命题正确的个数是(?? ????)
①平分弧的直径垂直平分弧所对的弦;②平分弦的直径平分弦所对的弧;③垂直于弦的直线必过圆心;④垂直于弦的直径平分弦所对的弧.
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
B
5.如图,?ABCD的顶点A、B、D在⊙O上,顶点C在⊙O的直径BE上,连接AE , ∠E=55°,则∠ADC的度数是(??? )
A.?55°???????????B.?45°????????????????C.?35°???????????????????D.?25°
C
6.如图 1 ,把圆形井盖卡在角尺〔角的两边互相垂直,一边有刻度)之间,即圆与两条直角边相切,现将角尺向右平移 10???????? ,如图 2 , ???????? 边与圆的两个交点对应 ???????? 的长为 40???????? ,则可知井盖的直径是( ??)
?
A.?25cm?????B.?30cm????????????C.?50cm??????????????????D.?60cm
C
7.四边形ABCD内接于⊙O,则∠A∶∠B∶∠C∶∠D的值可以是(?? )
A.?2∶3∶4∶5???????????????????????B.?2∶4∶3∶5???????????????????????C.?2∶5∶3∶4???????????????????????D.?2∶3∶5∶4
D
8.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=16cm,则球的半径为(?? )
A.?10 3 cm?????????????B.?10cm????????????????C.?10 2 cm?????????D.?8 3 cm
?
B
9. ???????? 是 ⊙???? 的直径, ???????? 是弦, ????????⊥???????? ,垂足为点 ???? ,连接 ???????? 、 ???????? 、 ???????? , ∠????????????=60? , ????????=2 ,那么 ???????? 的长为( ???)
?
A.?3??????B.?23?????????C.?33????????????D.?43
?
D
10.《九章算术》是我国古代第一部自成体系的数学专著,代表了东方数学的最高成就.它的算法体系至今仍在推动着计算机的发展和应用.书中记载:“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”译为:“今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这木材,锯口深1寸(ED=1寸),锯道长1尺(AB=1尺=10寸)”,问这块圆形木材的直径是多少?”
请根据所学知识计算:圆形木材的直径AC是(?? )
A.?13寸????? B.?20寸?????? ?C.?26寸?????????????????D.?28寸
C
11.如图,△ABC内接于圆O,若∠A=m° ,则∠OBC=________度(用含m的代数式表示)
12.已知⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=8cm,则AC的长为________.
25????????或45????????
?
13.如图,在△ABC中,AB=AC=10,以AB为直径的⊙O与BC交于点D,与AC交于点E,连接OD,交BE于点M且MD=2, 则BE长为________.
8
14.A(1,0)、B(3,0),以AB为直径作⊙M,射线OF交⊙M于E、F两点,C为弧AB 的中点,D为EF的中点.当射线OF绕O点旋转时,CD的最小值为________.
15.四边形ABCD内接于⊙O,E为直径CD延长线上一点,且AB∥CD,若∠C=70°,则∠ADE的大小为________.
110°
16.以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C,D两点,点E为⊙O上一动点,CF⊥AE于F,则弦AB的长度为________;点E在运动过程中,线段FG的长度的最小值为________.
23
?
3?1
?
17.已知:如图△ABC内接于圆O,AB=AC,D为弧BC上任意一点,连结AD,BD
(1)若∠ADB=65°,求∠BAC的度数
(2)求证:∠ABD=∠AEB
(1)解: ∵AB=AC
∴∠C=∠ABC,弧AB=弧AC
∴∠C=∠ABC=∠ADB=65°
∴∠BAC=(180°-65°×2)=50°
(2)证明: ∵∠AEB=∠DAC+∠C
∠ABD=∠ABC+∠DBC
∵弧CD=弧CD
∴∠DAC=∠DBC
∵∠ABC=∠C
∴∠ABD=∠AEB
18.已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D.
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆心O到直线AB的距离为6,求AC的长
(1)证明:过点O作OE⊥AB于E,
则CE=DE,AE=BE.
∴AE-CE=BE-DE
即AC=BD
(2)解:连接OC,OA
由(1)可知,OE⊥AB且OE⊥CD,
∴OE=6
∴CE= ????????2?????????2=82?62=27
AE= ????????2?????????2=102?62=8
∴AC=AE-CE=8-2 7
?
19.四边形ABCD内接于⊙O,AC平分∠BAD,延长DC交AB的延长线于点E.
(1)若∠ADC=86°,求∠CBE的度数;
(2)若AC=EC,求证:AD=BE
(1)解:∵四边形 ABCD 内接于⊙O,
∴∠ADC+∠ABC=180°,
∵∠CBE+∠ABC=180°,
∴∠ADC=∠CBE,
又∵∠ADC=86°,
∴∠CBE=86°.
(2)证明:∵AC=EC,
∴∠E=∠CAE,
∵AC 平分∠BAD,
∴∠DAC=∠CAB,
∴∠DAC=∠E,
又∵四边形 ABCD 内接于⊙O,
∴∠ADC+∠ABC=180°,
∵∠CBE+∠ABC=180°,
∴∠ADC=∠CBE,
在△ ADC 和△ EBC 中{∠????????????=∠????????????∠????????????=∠????????????=????????
∴△ADC≌△EBC(AAS),
∴AD=BE.
?
20.用工件槽(如图1)可以检测一种铁球的大小是否符合要求,已知工件槽的两个底角均为90°,尺寸如图(单位:cm).将形状规则的铁球放入槽内时,若同时具有图1所示的A、B、E三个接触点,该球的大小就符合要求.图2是过球心O及A、B、E三点的截面示意图,求这种铁球的直径.
20.解:连接OA、OE,设OE与AB交于点P,如图
∵AC=BD,AC⊥CD,BD⊥CD
∴四边形ACDB是矩形
∵CD=16cm,PE=4cm
∴PA=8cm,BP=8cm,
在Rt△OAP中,由勾股定理得OA2=PA2+OP2
即OA2=82+(OA﹣4)2
解得:OA=10.
答:这种铁球的直径为20cm.
21.如图,已知OA、OB、OC是⊙O的三条半径,点C是弧AB的中点,M、N分别是OA、OB的中点.求证:MC=NC.
.证明:∵点 C 是弧 AB 的中点,
∴ 弧 AC 和弧 BC 相等,
∴∠AOC=∠BOC,
又∵OA=OB,M、N 分别是 OA、OB 的中点,
∴OM=ON,
在△ MOC 和△ NOC 中,{????????=????????∠????????????=∠????????????????????=????????
∴△MOC≌△NOC(SAS),
∴MC=NC.
?
22.已知AB是⊙O的弦,OB=2,∠B=30°,C是弦AB上任意一点(不与点A、B重合),连接CO并延长CO交⊙O于点D,连接AD.
(1)弦长AB等于________(结果保留根号);
(2)当∠D=20°时,求∠BOD的度数.
23
?
(2)解:如图所示,连接OA,
因为OA=OB,OA=OD,所以
∠OAB=∠OBA=30°,
∠OAD=∠ODA=20°
∴∠CAD=50°
∴∠OCB=50°+20°=70°
∴∠BOD=∠OCB+∠B=100°
23.在圆内接四边形ABCD中,O为圆心,∠BOD=160°,求∠BCD的度数.
解:∵∠BOD=160°∴∠BAD= 12∠????????????=80?
∵A、B、C、D 四点共圆,
∴∠BCD+∠BAD=180°,
∴∠BCD=100°.
?
24.生活中看似平常的隧道设计也很精巧.如图是一张盾构隧道断面结构图,隧道内部为以O为圆心AB为直径的圆.隧道内部共分为三层,上层为排烟道,中间为行车隧道,下层为服务层.点A到顶棚的距离为0.8a,顶棚到路面的距离是3.2a,点B到路面的距离为2a.请你求出路面的宽度l.(用含a的式子表示)
解:如图,连接OC,AB交CD于E,
由题意知:AB=0.8a+3.2a+2a=6a,
所以OC=OB=3a,
OE=OB-BE=3a-2a=a,
由题意可知:AB⊥CD,
∵AB过O,
∴CD=2CE,
在Rt△OCE中,由勾股定理得:CE= ????????2?????????2 = (3????)2?????2 =2 2 a,
∴CD=2CE=4 2 a,
所以路面的宽度l为4 2 a.
?
课堂小结:
① 垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.
垂径定理的逆应用:圆心、中点,垂直
②圆周角与圆心角的关系
圆周角的度数等于它所对弧上的圆心角的度数一半.
在同圆或等圆中,同弧或等弧所对的圆周角相等
推论:直径所对的圆周角是直角,90°的圆周角所对的弦是直径.
谢谢观看
教学内容
1.垂经定理
2.圆周角与圆心角的关系
圆
1.1垂径定理
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
例1如图,AB是⊙O的直径,弦CD⊥AB,垂足为M,下列结论不一定成立的是( )
A.CM=DM
B.
C.∠ACD=∠ADC
D.OM=MD
例2.一条公路的转弯处是一段圆弦(即图中 ,点O是 的圆心,其中CD=600 m,E为上一点,且OE⊥CD,垂足为F,EF=90 m,求这段弯路的半径.
解:如图,连接OC,
设弯路的半径为R,则OF=(R-90) m.
∵OE⊥CD,∴CF=CD=×600=300(m).
根据勾股定理,得:OC2=CF2+OF2.
即R2=3002+(R-90)2,
解得R=545.∴这段弯路的半径为545 m.
(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧.
(3)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧
1.2垂径定理的逆定理:
例3.OC交AB于点D,AD=DB,AB=6 cm,CD=1 cm,求⊙O的半径长.
解:设圆的半径为r,则OB=OC=r,
∴32+(r-1)2=r2,
解得r=5 cm.
即⊙O的半径长为5 cm.
2.1圆周角与圆心角的关系
圆周角的度数等于它所对弧上的圆心角的度数一半.
在同圆或等圆中,同弧或等弧所对的圆周角相等.
2.1圆周角与圆心角的关系
例4已知BD是⊙O的直径,点A、C在⊙O上, ,∠AOB=60°,则∠BDC的度数是( )
A.20° B.25°
C.30° D.40°
解析:∵=,∠AOB=60°,
∴∠BDC=∠AOB=30°.
故选C.
例5.已知A,B,C在⊙O上,为优弧,下列选项中与∠AOB相等的是( )
A.2∠C B.4∠B
C.4∠A D.∠B+∠C
由圆周角定理可得:∠AOB=2∠C.
故选A.
2.2圆周角定理的推论
直径所对的圆周角是直角,90°的圆周角所对的弦是直径.
四边形的四个顶点都在圆上,这样的四边形叫做圆内接四边形.这个圆叫做四边形的外接圆.圆内接四边形的对角互补.
例6.⊙O的两弦AD,BC相交于点E,连接AC,BD,AO,BO.若∠ACB=60°,则下列结论正确的是( )
A.∠AOB=60° B.∠ADB=60°
C.∠AEB=60° D.∠AEB=30°
解析:由圆周角定理及推论可知,
,∠ACB=∠ADB.
∵∠ACB=60°,
∴∠AOB=120°,∠ADB=60°.
答案:B
例7.△ABC为⊙O的内接三角形,若∠AOC=160°,则∠ABC的度数是( )
A.80° B.160° C.100° D.80°或100°
解析:当点B在优弧 上时,∠ABC=2∠AOC=×160°=80°.
当点B在劣弧 上时,∠AB′C=180°-∠ABC=180°-80°=100°.
所以∠ABC的度数是80°或100°.
答案:D
随堂练习:
1.AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OE∥AC交半圆O于点E,过点E作EF⊥AB于F.若AC=2,则OF的长为(?? )
??????????????????
C
2.边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则∠BED的正切值等于(??? )
3.已知点E在半径为5的⊙O上运动,AB是⊙O的弦且AB=8,则使△ABE的面积为8 的点E共有( ?????)个??
A.??? 1??????????????????????????????????????????B.?2??????????????????????????????????????????C.?3??????????????????????????????????????????D.?4
C
4.下列命题正确的个数是(?? ????)
①平分弧的直径垂直平分弧所对的弦;②平分弦的直径平分弦所对的弧;③垂直于弦的直线必过圆心;④垂直于弦的直径平分弦所对的弧.
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
B
5.如图,?ABCD的顶点A、B、D在⊙O上,顶点C在⊙O的直径BE上,连接AE , ∠E=55°,则∠ADC的度数是(??? )
A.?55°???????????B.?45°????????????????C.?35°???????????????????D.?25°
C
6.如图 1 ,把圆形井盖卡在角尺〔角的两边互相垂直,一边有刻度)之间,即圆与两条直角边相切,现将角尺向右平移 10???????? ,如图 2 , ???????? 边与圆的两个交点对应 ???????? 的长为 40???????? ,则可知井盖的直径是( ??)
?
A.?25cm?????B.?30cm????????????C.?50cm??????????????????D.?60cm
C
7.四边形ABCD内接于⊙O,则∠A∶∠B∶∠C∶∠D的值可以是(?? )
A.?2∶3∶4∶5???????????????????????B.?2∶4∶3∶5???????????????????????C.?2∶5∶3∶4???????????????????????D.?2∶3∶5∶4
D
8.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=16cm,则球的半径为(?? )
A.?10 3 cm?????????????B.?10cm????????????????C.?10 2 cm?????????D.?8 3 cm
?
B
9. ???????? 是 ⊙???? 的直径, ???????? 是弦, ????????⊥???????? ,垂足为点 ???? ,连接 ???????? 、 ???????? 、 ???????? , ∠????????????=60? , ????????=2 ,那么 ???????? 的长为( ???)
?
A.?3??????B.?23?????????C.?33????????????D.?43
?
D
10.《九章算术》是我国古代第一部自成体系的数学专著,代表了东方数学的最高成就.它的算法体系至今仍在推动着计算机的发展和应用.书中记载:“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”译为:“今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这木材,锯口深1寸(ED=1寸),锯道长1尺(AB=1尺=10寸)”,问这块圆形木材的直径是多少?”
请根据所学知识计算:圆形木材的直径AC是(?? )
A.?13寸????? B.?20寸?????? ?C.?26寸?????????????????D.?28寸
C
11.如图,△ABC内接于圆O,若∠A=m° ,则∠OBC=________度(用含m的代数式表示)
12.已知⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=8cm,则AC的长为________.
25????????或45????????
?
13.如图,在△ABC中,AB=AC=10,以AB为直径的⊙O与BC交于点D,与AC交于点E,连接OD,交BE于点M且MD=2, 则BE长为________.
8
14.A(1,0)、B(3,0),以AB为直径作⊙M,射线OF交⊙M于E、F两点,C为弧AB 的中点,D为EF的中点.当射线OF绕O点旋转时,CD的最小值为________.
15.四边形ABCD内接于⊙O,E为直径CD延长线上一点,且AB∥CD,若∠C=70°,则∠ADE的大小为________.
110°
16.以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C,D两点,点E为⊙O上一动点,CF⊥AE于F,则弦AB的长度为________;点E在运动过程中,线段FG的长度的最小值为________.
23
?
3?1
?
17.已知:如图△ABC内接于圆O,AB=AC,D为弧BC上任意一点,连结AD,BD
(1)若∠ADB=65°,求∠BAC的度数
(2)求证:∠ABD=∠AEB
(1)解: ∵AB=AC
∴∠C=∠ABC,弧AB=弧AC
∴∠C=∠ABC=∠ADB=65°
∴∠BAC=(180°-65°×2)=50°
(2)证明: ∵∠AEB=∠DAC+∠C
∠ABD=∠ABC+∠DBC
∵弧CD=弧CD
∴∠DAC=∠DBC
∵∠ABC=∠C
∴∠ABD=∠AEB
18.已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D.
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆心O到直线AB的距离为6,求AC的长
(1)证明:过点O作OE⊥AB于E,
则CE=DE,AE=BE.
∴AE-CE=BE-DE
即AC=BD
(2)解:连接OC,OA
由(1)可知,OE⊥AB且OE⊥CD,
∴OE=6
∴CE= ????????2?????????2=82?62=27
AE= ????????2?????????2=102?62=8
∴AC=AE-CE=8-2 7
?
19.四边形ABCD内接于⊙O,AC平分∠BAD,延长DC交AB的延长线于点E.
(1)若∠ADC=86°,求∠CBE的度数;
(2)若AC=EC,求证:AD=BE
(1)解:∵四边形 ABCD 内接于⊙O,
∴∠ADC+∠ABC=180°,
∵∠CBE+∠ABC=180°,
∴∠ADC=∠CBE,
又∵∠ADC=86°,
∴∠CBE=86°.
(2)证明:∵AC=EC,
∴∠E=∠CAE,
∵AC 平分∠BAD,
∴∠DAC=∠CAB,
∴∠DAC=∠E,
又∵四边形 ABCD 内接于⊙O,
∴∠ADC+∠ABC=180°,
∵∠CBE+∠ABC=180°,
∴∠ADC=∠CBE,
在△ ADC 和△ EBC 中{∠????????????=∠????????????∠????????????=∠????????????=????????
∴△ADC≌△EBC(AAS),
∴AD=BE.
?
20.用工件槽(如图1)可以检测一种铁球的大小是否符合要求,已知工件槽的两个底角均为90°,尺寸如图(单位:cm).将形状规则的铁球放入槽内时,若同时具有图1所示的A、B、E三个接触点,该球的大小就符合要求.图2是过球心O及A、B、E三点的截面示意图,求这种铁球的直径.
20.解:连接OA、OE,设OE与AB交于点P,如图
∵AC=BD,AC⊥CD,BD⊥CD
∴四边形ACDB是矩形
∵CD=16cm,PE=4cm
∴PA=8cm,BP=8cm,
在Rt△OAP中,由勾股定理得OA2=PA2+OP2
即OA2=82+(OA﹣4)2
解得:OA=10.
答:这种铁球的直径为20cm.
21.如图,已知OA、OB、OC是⊙O的三条半径,点C是弧AB的中点,M、N分别是OA、OB的中点.求证:MC=NC.
.证明:∵点 C 是弧 AB 的中点,
∴ 弧 AC 和弧 BC 相等,
∴∠AOC=∠BOC,
又∵OA=OB,M、N 分别是 OA、OB 的中点,
∴OM=ON,
在△ MOC 和△ NOC 中,{????????=????????∠????????????=∠????????????????????=????????
∴△MOC≌△NOC(SAS),
∴MC=NC.
?
22.已知AB是⊙O的弦,OB=2,∠B=30°,C是弦AB上任意一点(不与点A、B重合),连接CO并延长CO交⊙O于点D,连接AD.
(1)弦长AB等于________(结果保留根号);
(2)当∠D=20°时,求∠BOD的度数.
23
?
(2)解:如图所示,连接OA,
因为OA=OB,OA=OD,所以
∠OAB=∠OBA=30°,
∠OAD=∠ODA=20°
∴∠CAD=50°
∴∠OCB=50°+20°=70°
∴∠BOD=∠OCB+∠B=100°
23.在圆内接四边形ABCD中,O为圆心,∠BOD=160°,求∠BCD的度数.
解:∵∠BOD=160°∴∠BAD= 12∠????????????=80?
∵A、B、C、D 四点共圆,
∴∠BCD+∠BAD=180°,
∴∠BCD=100°.
?
24.生活中看似平常的隧道设计也很精巧.如图是一张盾构隧道断面结构图,隧道内部为以O为圆心AB为直径的圆.隧道内部共分为三层,上层为排烟道,中间为行车隧道,下层为服务层.点A到顶棚的距离为0.8a,顶棚到路面的距离是3.2a,点B到路面的距离为2a.请你求出路面的宽度l.(用含a的式子表示)
解:如图,连接OC,AB交CD于E,
由题意知:AB=0.8a+3.2a+2a=6a,
所以OC=OB=3a,
OE=OB-BE=3a-2a=a,
由题意可知:AB⊥CD,
∵AB过O,
∴CD=2CE,
在Rt△OCE中,由勾股定理得:CE= ????????2?????????2 = (3????)2?????2 =2 2 a,
∴CD=2CE=4 2 a,
所以路面的宽度l为4 2 a.
?
课堂小结:
① 垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.
垂径定理的逆应用:圆心、中点,垂直
②圆周角与圆心角的关系
圆周角的度数等于它所对弧上的圆心角的度数一半.
在同圆或等圆中,同弧或等弧所对的圆周角相等
推论:直径所对的圆周角是直角,90°的圆周角所对的弦是直径.
谢谢观看
