北师大版九年级数学下册课件:第三章圆第三讲确定圆的条件、圆与直线的位置关系以及圆的相关计算(共24张PPT)
文档属性
| 名称 | 北师大版九年级数学下册课件:第三章圆第三讲确定圆的条件、圆与直线的位置关系以及圆的相关计算(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-19 00:00:00 | ||
图片预览



文档简介
第三节
教学内容
1.确定圆的条件
2. 直线与圆的位置关系
3.切线长定理
4.圆的内接正多边形
圆
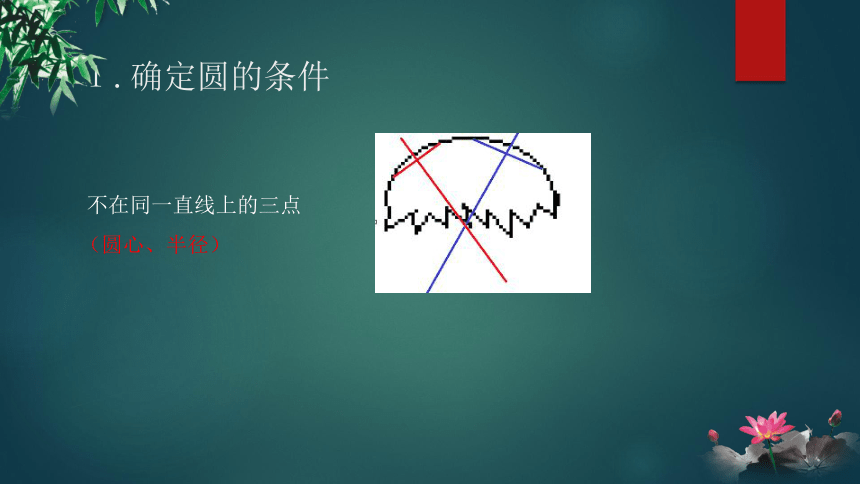
1.确定圆的条件
不在同一直线上的三点
(圆心、半径)
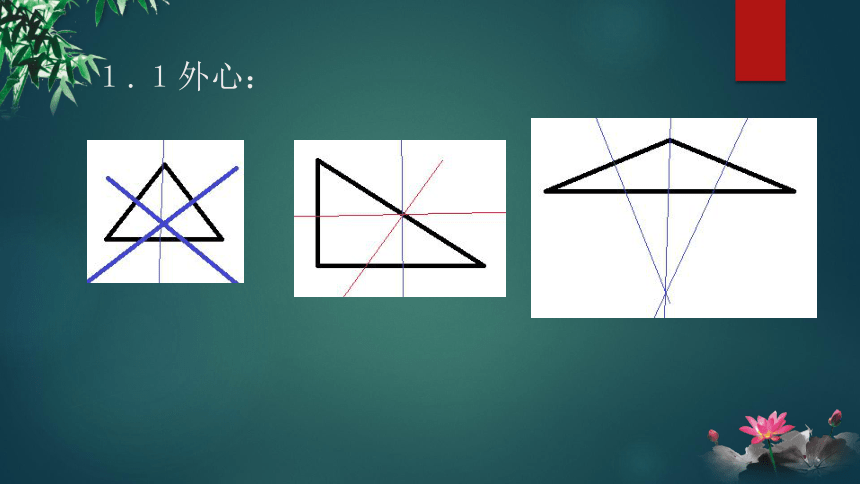
1.1外心:
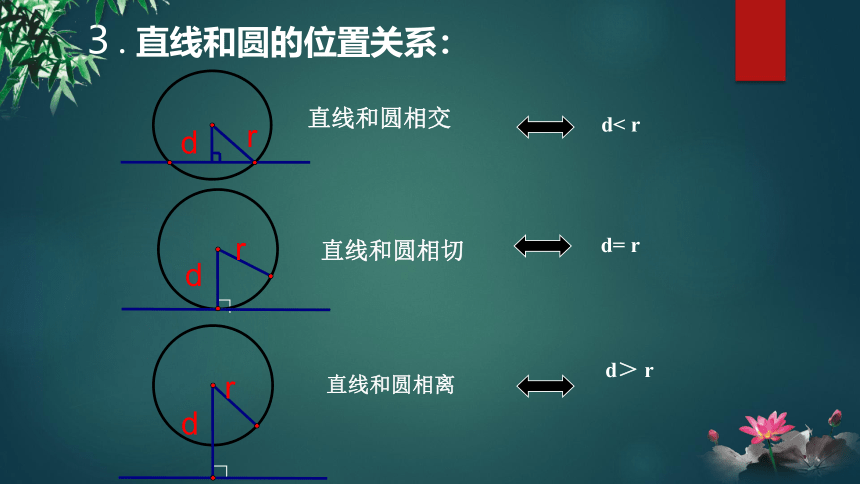
3.直线和圆的位置关系:
r
d
∟
r
d
∟
r
d
直线和圆相交
d< r
直线和圆相切
d> r
直线和圆相离
d= r
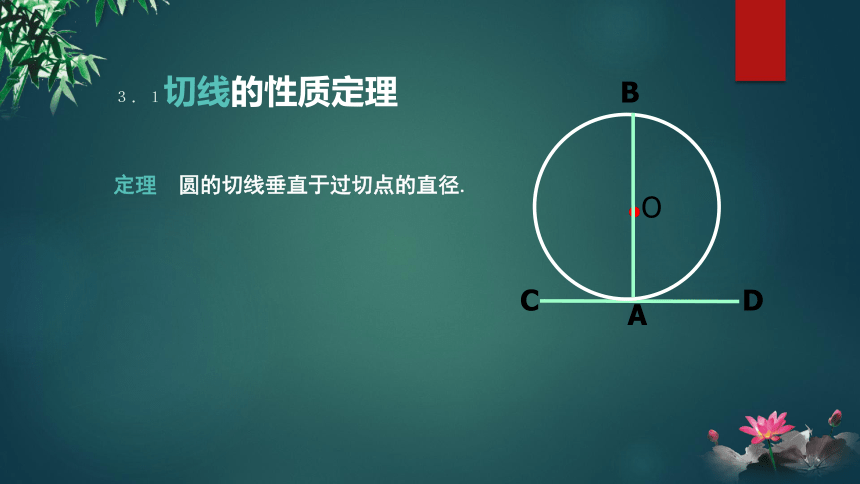
3.1切线的性质定理
定理 圆的切线垂直于过切点的直径.
C
D
B
●O
A
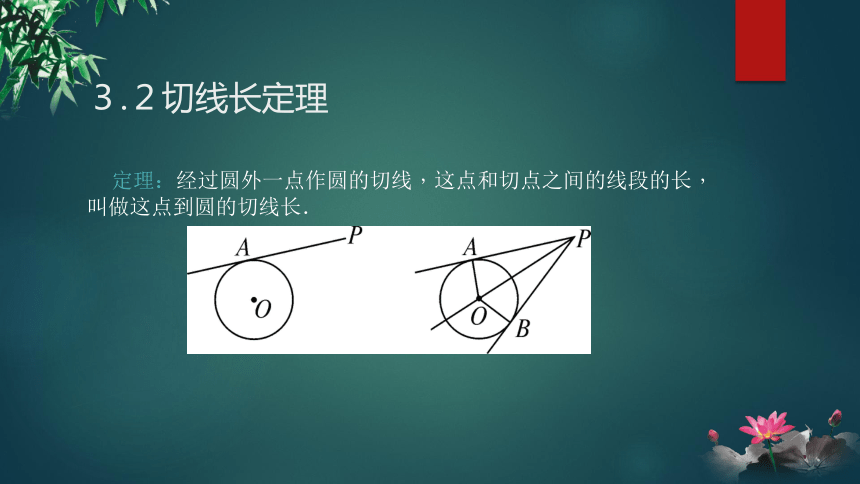
3.2切线长定理
定理:经过圆外一点作圆的切线,这点和切点之间的线段的长,叫做这点到圆的切线长.
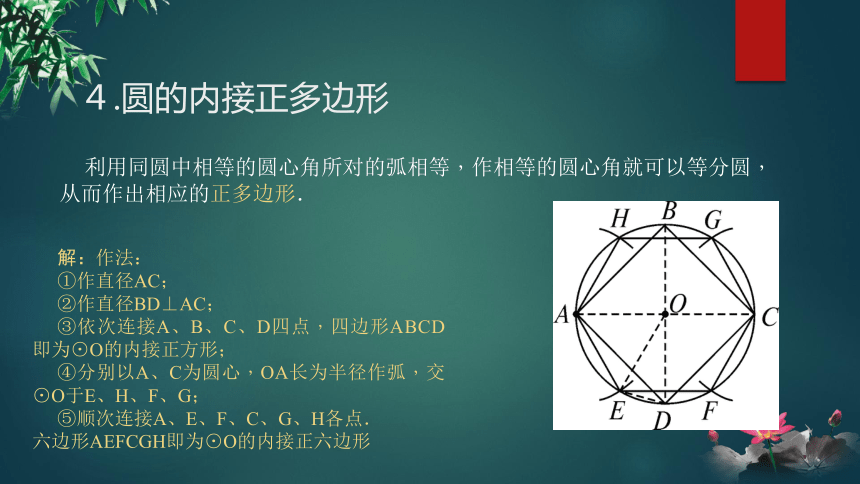
4.圆的内接正多边形
利用同圆中相等的圆心角所对的弧相等,作相等的圆心角就可以等分圆,从而作出相应的正多边形.
解:作法:
①作直径AC;
②作直径BD⊥AC;
③依次连接A、B、C、D四点,四边形ABCD即为⊙O的内接正方形;
④分别以A、C为圆心,OA长为半径作弧,交⊙O于E、H、F、G;
⑤顺次连接A、E、F、C、G、H各点.
六边形AEFCGH即为⊙O的内接正六边形
5.弧长及扇形面积
例1.已知Rt△ABC的斜边AB=8cm,直角边AC=4cm.
(1)以点C为圆心作圆,当半径为多长时,AB与⊙C相切?
(2)以点C为圆心,分别以2cm,4cm为半径作两个圆,这两个圆与AB分别有怎样的位置关系?
D
解:(1)过点C作CD⊥AB于D.
∵AB=8cm,AC=4cm.
∴∠A=60°
(2)由(1)可知,圆心到AB的距离
d= cm
∴当r=2cm时,d>r,AB与⊙C相离;
∴当r=2cm时,d>r,AB与⊙C相离;
例2.已知⊙O的半径是6,点O到直线l的距离为5,则直线l与⊙O的位置关系是( )
A.相离 B.相切 C.相交 D.无法判断
解:∵⊙O的半径为6,圆心O到直线l的距离为5,∵6>5,即:d∴直线l与⊙O的位置关系是相交.故选C.
例3.Rt△ABC中,∠C=90°,AC=3 cm,BC=4 cm,以C为圆心,r为半径作圆,若圆C与直线AB相切,则r的值为( )
A.2 cm B.2.4 cm C.3 cm D.4 cm
解析:Rt△ABC中,∠C=90°,AC=3 cm,BC=4 cm;
由勾股定理,得:AB2=32+42=25,∴AB=5 cm;
又∵AB是⊙C的切线,设切点为D,∴CD⊥AB,∴CD=r.
∵S△ABC=AC·BC=AB·r.∴r=2.4 cm,故选B.
例4.下列直线中一定是圆的切线的是( )
A.与圆有公共点的直线 B.到圆心的距离等于半径的直线
C.垂直于圆的半径的直线 D.过圆的直径端点的直线
解析:根据切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.A有可能是割线,B距离就表明垂直关系,距离又等于半径就表明经过半径的外端.所以是对的,C也有可能是割线,D过圆的直径端点的直线不一定垂直.
答案:B
例5.AB是⊙O的直径,∠ABT=45°,AT=AB.求证:AT是⊙O的切线.
证明:∵AB=AT,∠ABT=45°.
∴∠ATB=∠ABT=45°,
∴∠TAB=180°-∠ABT-∠ATB=90°,
∴AT⊥AB,即AT是⊙O的切线.
例6.下列说法中,正确的是( )
A.垂直于半径的直线一定是这个圆的切线
B.圆有且只有一个外切三角形
C.三角形有且只有一个内切圆
D.三角形的内心到三角形的三个顶点的距离相等
?
解析:A有可能是割线;B外切三角形是指三角形的三边与圆相切,这样的三角形有无数个;C内切圆的圆心是三角形三角的角平分线的交点,这样的交点只有一个,所以正确;D应该是到三边的距离相等.故选C.
例7.如图,⊙O内切Rt△ABC,切点分别是D、E、F,则四边形OECF是________.
解析:根据切线的性质可得∠OFC=∠OEC=90°且∠ACB=90°.
所以四边形OECF是矩形.再根据三角形的内心可得OE=OF.
所以四边形OECF是正方形.
答案:正方形
例8.△ABC中,O是内心,∠A的平分线和△ABC的外接圆相交于点D,求证:DO=DB.
证明:连接OB,
∵点O是△ABC的内心,∴∠1=∠2,∠3=∠4.
∵∠2=∠5,∴∠1=∠5.∵∠BOD=∠1+∠3,
∠OBD=∠5+∠4,
∴∠BOD=∠OBD.∴DO=DB.
例8.AE、AD、BC分别切⊙O于点E、D、F,若AD=20,求△ABC的周长.
解:∵AD,AE切于⊙O于D,E,
∴AD=AE=20,
∵AD,BF切于⊙O于D,F,
∴BD=BF,同理:CF=CE.
∴C△ABC=AB+BC+AC=AB+BF+FC+AC
=AB+BD+EC+AC=AD+AE=40.
例9.PA、PB是⊙O的两条切线,切点分别为点A、B,若直径AC=12,∠P=60°,求弦AB的长.
解:连接BC.
∵PA,PB切⊙O于A,B,∴PA=PB.
∵∠P=60°,∴△ABP是正三角形.
∵∠PAB=60°,∴PA是⊙O切线.
∴CA⊥AP.
∴∠CAP=90°.∴∠CAB=30°
∵直径AC,∴∠ABC=90°.
∴AB=6.
例10.正三角形的高、外接圆半径、边心距之比为( )
A.3∶2∶1 B.4∶3∶2 B.4∶2∶1 D.6∶4∶3
A
例11.制作弯形管道时,需要先按中心线计算“展直长度”再下料,试计算下图中管道的展直长度,即AB的长(结果精确到0.1 mm).
课堂小结:
① 确定圆的条件:不在一条线上的三点
② 圆与直线的位置关系:交、切、离
③ 切线长定理:经过圆外一点作圆的切线,这点和切点之间的线段的长,叫做这点到圆的切线长.
4.圆的内接正多边形 :
5.弧长公式:
扇形面积公式:
谢谢观看
创意中国风/学校教育/论文答辩
教学内容
1.确定圆的条件
2. 直线与圆的位置关系
3.切线长定理
4.圆的内接正多边形
圆
1.确定圆的条件
不在同一直线上的三点
(圆心、半径)
1.1外心:
3.直线和圆的位置关系:
r
d
∟
r
d
∟
r
d
直线和圆相交
d< r
直线和圆相切
d> r
直线和圆相离
d= r
3.1切线的性质定理
定理 圆的切线垂直于过切点的直径.
C
D
B
●O
A
3.2切线长定理
定理:经过圆外一点作圆的切线,这点和切点之间的线段的长,叫做这点到圆的切线长.
4.圆的内接正多边形
利用同圆中相等的圆心角所对的弧相等,作相等的圆心角就可以等分圆,从而作出相应的正多边形.
解:作法:
①作直径AC;
②作直径BD⊥AC;
③依次连接A、B、C、D四点,四边形ABCD即为⊙O的内接正方形;
④分别以A、C为圆心,OA长为半径作弧,交⊙O于E、H、F、G;
⑤顺次连接A、E、F、C、G、H各点.
六边形AEFCGH即为⊙O的内接正六边形
5.弧长及扇形面积
例1.已知Rt△ABC的斜边AB=8cm,直角边AC=4cm.
(1)以点C为圆心作圆,当半径为多长时,AB与⊙C相切?
(2)以点C为圆心,分别以2cm,4cm为半径作两个圆,这两个圆与AB分别有怎样的位置关系?
D
解:(1)过点C作CD⊥AB于D.
∵AB=8cm,AC=4cm.
∴∠A=60°
(2)由(1)可知,圆心到AB的距离
d= cm
∴当r=2cm时,d>r,AB与⊙C相离;
∴当r=2cm时,d>r,AB与⊙C相离;
例2.已知⊙O的半径是6,点O到直线l的距离为5,则直线l与⊙O的位置关系是( )
A.相离 B.相切 C.相交 D.无法判断
解:∵⊙O的半径为6,圆心O到直线l的距离为5,∵6>5,即:d
例3.Rt△ABC中,∠C=90°,AC=3 cm,BC=4 cm,以C为圆心,r为半径作圆,若圆C与直线AB相切,则r的值为( )
A.2 cm B.2.4 cm C.3 cm D.4 cm
解析:Rt△ABC中,∠C=90°,AC=3 cm,BC=4 cm;
由勾股定理,得:AB2=32+42=25,∴AB=5 cm;
又∵AB是⊙C的切线,设切点为D,∴CD⊥AB,∴CD=r.
∵S△ABC=AC·BC=AB·r.∴r=2.4 cm,故选B.
例4.下列直线中一定是圆的切线的是( )
A.与圆有公共点的直线 B.到圆心的距离等于半径的直线
C.垂直于圆的半径的直线 D.过圆的直径端点的直线
解析:根据切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.A有可能是割线,B距离就表明垂直关系,距离又等于半径就表明经过半径的外端.所以是对的,C也有可能是割线,D过圆的直径端点的直线不一定垂直.
答案:B
例5.AB是⊙O的直径,∠ABT=45°,AT=AB.求证:AT是⊙O的切线.
证明:∵AB=AT,∠ABT=45°.
∴∠ATB=∠ABT=45°,
∴∠TAB=180°-∠ABT-∠ATB=90°,
∴AT⊥AB,即AT是⊙O的切线.
例6.下列说法中,正确的是( )
A.垂直于半径的直线一定是这个圆的切线
B.圆有且只有一个外切三角形
C.三角形有且只有一个内切圆
D.三角形的内心到三角形的三个顶点的距离相等
?
解析:A有可能是割线;B外切三角形是指三角形的三边与圆相切,这样的三角形有无数个;C内切圆的圆心是三角形三角的角平分线的交点,这样的交点只有一个,所以正确;D应该是到三边的距离相等.故选C.
例7.如图,⊙O内切Rt△ABC,切点分别是D、E、F,则四边形OECF是________.
解析:根据切线的性质可得∠OFC=∠OEC=90°且∠ACB=90°.
所以四边形OECF是矩形.再根据三角形的内心可得OE=OF.
所以四边形OECF是正方形.
答案:正方形
例8.△ABC中,O是内心,∠A的平分线和△ABC的外接圆相交于点D,求证:DO=DB.
证明:连接OB,
∵点O是△ABC的内心,∴∠1=∠2,∠3=∠4.
∵∠2=∠5,∴∠1=∠5.∵∠BOD=∠1+∠3,
∠OBD=∠5+∠4,
∴∠BOD=∠OBD.∴DO=DB.
例8.AE、AD、BC分别切⊙O于点E、D、F,若AD=20,求△ABC的周长.
解:∵AD,AE切于⊙O于D,E,
∴AD=AE=20,
∵AD,BF切于⊙O于D,F,
∴BD=BF,同理:CF=CE.
∴C△ABC=AB+BC+AC=AB+BF+FC+AC
=AB+BD+EC+AC=AD+AE=40.
例9.PA、PB是⊙O的两条切线,切点分别为点A、B,若直径AC=12,∠P=60°,求弦AB的长.
解:连接BC.
∵PA,PB切⊙O于A,B,∴PA=PB.
∵∠P=60°,∴△ABP是正三角形.
∵∠PAB=60°,∴PA是⊙O切线.
∴CA⊥AP.
∴∠CAP=90°.∴∠CAB=30°
∵直径AC,∴∠ABC=90°.
∴AB=6.
例10.正三角形的高、外接圆半径、边心距之比为( )
A.3∶2∶1 B.4∶3∶2 B.4∶2∶1 D.6∶4∶3
A
例11.制作弯形管道时,需要先按中心线计算“展直长度”再下料,试计算下图中管道的展直长度,即AB的长(结果精确到0.1 mm).
课堂小结:
① 确定圆的条件:不在一条线上的三点
② 圆与直线的位置关系:交、切、离
③ 切线长定理:经过圆外一点作圆的切线,这点和切点之间的线段的长,叫做这点到圆的切线长.
4.圆的内接正多边形 :
5.弧长公式:
扇形面积公式:
谢谢观看
创意中国风/学校教育/论文答辩
