北师大版九年级数学下册课件:第三章圆第一讲认识圆以及圆与直线的位置关系(共25张PPT)
文档属性
| 名称 | 北师大版九年级数学下册课件:第三章圆第一讲认识圆以及圆与直线的位置关系(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-19 09:34:51 | ||
图片预览







文档简介
第一讲
教学内容
1.圆的概念
2.圆的有关概念
4.圆的对称性
圆
3.点和圆的位置关系
1.圆的概念
在平面内,圆是到定点的距离等于定长的所有的点组成的图形.这个定点就是圆心,定长是半径.以点O为圆心的圆,记作⊙O,读作“圆O”.
2.与圆相关的概念
(1)连接圆上任意两点的线段叫做弦,如图①线段AC,AB;
(2)经过圆心的弦叫做直径,如图①线段AB;
(3)圆上任意两点间的部分叫做圆弧,简称弧,“以A、C为端点的弧记作”读作“圆弧AC”或“弧AC”.大于半圆的弧(如图①所示)叫做优弧,小于半圆的弧(如图①所示)或叫做劣弧;
与圆相关的概念
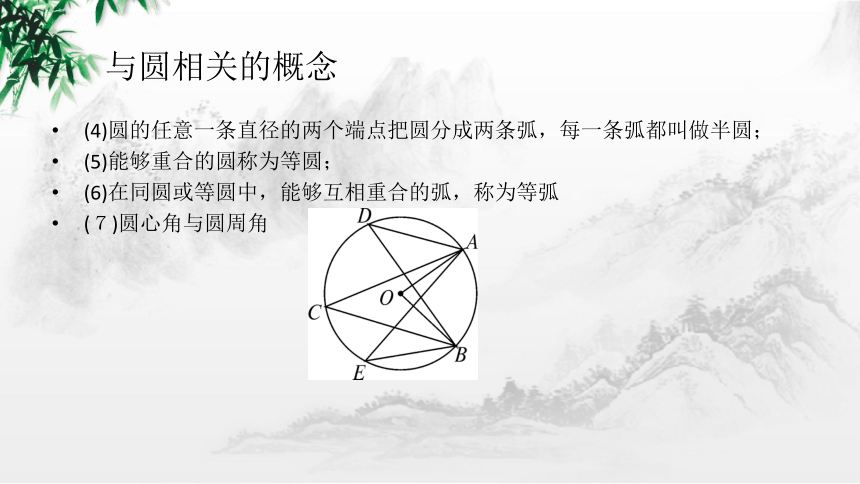
(4)圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆;
(5)能够重合的圆称为等圆;
(6)在同圆或等圆中,能够互相重合的弧,称为等弧
(7)圆心角与圆周角
3.点和圆的位置关系
如图②所示,设⊙O的半径为r,点到圆心的距离为d.
则有:点P在圆外d>r;点P在圆上d=r;点P在圆内d<r.
4.圆的对称性
1.圆是轴对称图形,对称轴是任意一条过圆心直线.
2.圆是中心对称图形,对称中心是圆心.
3.在同圆或等圆中,如果圆心角相等,那么它们所对的弧相等,所对的弦相等.
4.推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中的一组量相等,那么他们对应的其余各组量都分别相等.
运用新知,深化理解
1.判断:
(1)直径是弦.( )
(2)弦是直径.( )
(3)半圆是弧,但弧不一定是半圆.( )
(4)半径相等的两个半圆是等弧.( )
(5)长度相等的两条弧是等弧.( )
(6)周长相等的圆是等圆.( )
(7)面积相等的圆是等圆.( )
(8)优弧一定比劣弧长.( )
√
×
√
√
×
√
√
×
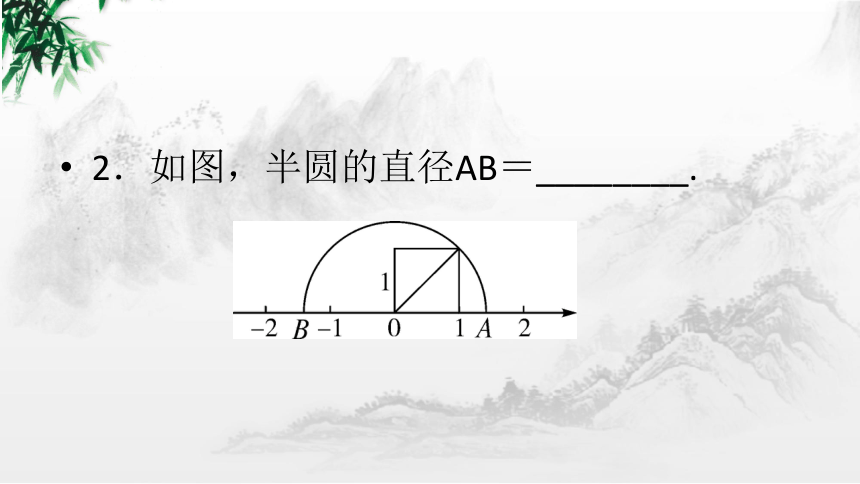
2.如图,半圆的直径AB=________.
3.点A在以O为圆心,3 cm为半径的⊙O内,则点A到圆心O的距离d的范围是________.
解析:根据点和圆的位置关系判定.
答案:0≤d<3.
4.下列说法正确的是( )
A.相等的圆心角所对的弧相等
B.在同圆中,等弧所对的圆心角相等
C.相等的弦所对的圆心到弦的距离相等
D.圆心到弦的距离相等,则弦相等
B
5.如图,AB、AC、BC都是⊙O的弦,∠AOC=∠BOC,∠ABC与∠BAC相等吗?为什么?
解:∵∠AOC=∠BOC,
∴AC=BC.(在同圆或等圆中,如果圆心角相等,那么它们所对的弧相等,所对的弦相等)
∴∠ABC=∠BAC.
随堂练习
1.已知AB是半径为5的圆的一条弦,则AB的长不可能是(?? )
A.?4?????????????????????????B.?8?????????????????C.?10??????????????????????D.?12
2.下列说法①直径是弦②半圆是弧③弦是直径④弧是半圆,其中正确的有(? ?)
3.如图,数轴上有A,B,C三点,点A,C关于点B对称,以原点O为圆心作圆,若点A,B,C分别在 ⊙???? ?外, ⊙???? 内, ⊙???? 上,则原点O的位置应该在(?? )
?
A.?点A与点B之间靠近A点???????????????????????????????????????B.?点A与点B之间靠近B点
C.?点B与点C之间靠近B点????????????????????????????????????????D.?点B与点C之间靠近C点
D
B
C
4.两圆的圆心都是O,半径分别为r1 , r2(r1A.?大圆外??????????????????B.?小圆内????????????????????C.?大圆内,小圆外?????????????????D.?无法确定
5.⊙O的半径为4,圆心O的坐标为(0,0),点P的坐标为(4,2),则点P与⊙O的位置关系是(??? )
A.?点P在⊙O内????????????????B.?点P的⊙O上????????????????C.?点P在⊙O外????????????????D.?点P在⊙O上或⊙O外
6.如图,在网格中(每个小正方形的边长均为1个单位)选取9个格点(格线的交点称为格点).如果以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为(?? )
A.?2 2 <r< 17?????????????????B.?17 <r<3 2???????????????
??C.?17 <r<5?????????????????D.?5<r< 29
?
C
C
B
7.如图,四边形PAOB是扇形OMN的内接矩形,顶点P在 ???????? 上,且不与M、N重合,当P点在 ???????? 上移动时,矩形PAOB的形状,大小随之变化,则AB的长度(?? )
?
A.?不变?????????????B.?变小??????????C.?变大?????????????D.?不能确定
8.如图点A,D,G,B在半圆上,四边形ABOC,DEOF,HMNO均为矩形,设BC=a, EF=b, NH=c,则下列说法正确的是(??? )
A.?a>b>c???????????B.?a=b=c ????????????C.?c>a>b?????????????D.?b>c>a?
A
B
9.在Rt△ABC中 ,∠C=90°,AC=2 , BC=4,若以点C为圆心,AC为半径作圆,则AB边的中点E与⊙C的位置关系为________.
10.已知⊙O的直径是方程 ????2?2?????12=0 的根,且点A到点O的距离是6,则点A与⊙O的位置关系是________.
?
11.如图,在矩形 ???????????????? 中, ????????=3 , ????????=4 ,若以点 ???? 为圆心,以 4 为半径作 ⊙???? ,则点 ???? ,点 ???? ,点 ???? ,点 ???? 四点中在 ⊙???? 外的是________.
?
点E在⊙C外
点A在圆外
点 C
?
12.平面上有⊙O及一点P,P到⊙O上一点的距离最长为6cm,最短为2cm,则⊙O的半径为________cm.
13.爆炸区 50???? 内是危险区,一人在离爆炸中心 ???? 点 30???? 的 ???? 处(如图),这人沿射线________的方向离开最快,离开________ ???? 无危险
?
14.在矩形ABCD中,AB=3,AD=4,以点A为圆心,r为半径画圆,若使点B在⊙A内,点C在⊙A外,则半径r的取值范围是________.
14.3<r<5
20
?
OA
4或2
15.⊙O的半径r=10cm,圆心O到直线l的距离OD=6cm,在直线l上有A、B、C三点,且AD=6cm,BD=8cm,CD=5 3 cm,问:A、B、C三点与⊙O的位置关系各是怎样?
?
解:∵OA= ????????2+????????2 = 62+62 = 72 (cm)<r=10cm,
OB= ????????2+????????2 = 62+82 =10(cm)=r,
OC= ????????2+????????2 = 62+(53)2 = 111 (cm)>r=10cm,
∴点A在⊙O内,点B在⊙O上,点C在⊙O外.
?
16.⊙O的半径r=10cm,圆心O到直线l的距离OD=6cm,在直线l上有A、B、C三点,且AD=6cm,BD=8cm,CD=5 3 cm,问:A、B、C三点与⊙O的位置关系各是怎样?
16.如图,已知AB,CB为⊙O的两条弦,请写出图中所有的弧.
?
图中的弧为 ????????,????????,????????,????????????,????????????,????????????.
?
17.已知:如图,△ABC中, ∠????=90° , ????????=2 ?cm, ????????=4 cm,CM是中线,以C为圆心,以 5 cm长为半径画圆,则点A、B、M与⊙C的关系如何?
?
解:在Rt△ABC中,由勾股定理得,
????????=42+22=25 (cm);
∵ ????????=2 cm <5 cm,
∴点A在⊙O内;
∵ ????????=4 cm >5 cm,
∴点B在⊙C外;
∵ ∠????=90° ,CM斜边上的是中线,
∴ ????????=12????????=5 cm
∴M点在⊙C上.
?
18.在△ABC中,∠C=90°,AC=4,AB=5,以点C为圆心,以r=3为半径作圆,判断A,B两点和⊙C的位置关系.
解:∵∠C=90°,AC=4,AB=5,
∴BC=3.
∵AC=4>r,
∴点A在⊙C外.
∵BC=3=r,
∴点B在⊙C上.
19.以矩形ABCD的顶点A为圆心画⊙A,使得B、C、D中至少有一点在⊙A内,且至少有一点在⊙A外,若BC=12,CD=5.求⊙A的半径r的取值范围。
解:根据题意画图如右,
因为BC=12,CD=5,所以????????=122+52=169=13。若想使得B、C、D中至少有一点在⊙A内,且至少有一点在⊙A外,则第一种情况为:B点在圆内,C、D点在圆外;第二种情况:B、D点在圆内,C点在圆外。综合两种情况来看,5?
20.如图,在直角梯形ABCD中,AD∥BC, ????????=1 , ????????=9 ,M为AB的中点,以CD为直径画圆P.
?
(1)当点M在圆P外时,求CD的长的取值范围;
(2)当点M在圆P上时,求CD的长;
(3)当点M在圆P内时,求CD的长的取值范围.
(1)解:取CD的中点P,连接MP,
∵M为AB的中点,
∴MP是梯形ABCD的中位线.
∵ ????????=1 , ????????=9 ,
∴ ????????=12×(1+9)=5 ,
∵点M在圆P外,
∴ ????????>???????? ,即 2????????>???????? ,
∴ 0?
(2)解:∵点M在圆P上,
∴ ????????=???????? ,即 2????????=???????? ,
∴ ????????=2×5=10
(3)解:∵点M在圆P内,
∴ ????????∴ ????????>10 .
?
21.城市 ???? 的正北方向 50???????? 的 ???? 处,有一无线电信号发射塔.已知,该发射塔发射的无线电信号的有效半径为 100???????? , ???????? 是一条直达 ???? 城的公路,从 ???? 城发往 ???? 城的班车速度为 60????????/h .
?
(1)当班车从 ???? 城出发开往 ???? 城时,某人立即打开无线电收音机,班车行驶了 0.5h 的时候接收信号最强.此时,班车到发射塔的距离是多少千米?(离发射塔越近,信号越强)
(2)班车从 ???? 城到 ???? 城共行驶了 2h ,请你判断到 ???? 城后还能接收到信号吗?请说明理由.
?
(1)解:过点 ???? 作 ????????⊥???????? 于点 ???? ,
设班车行驶了 0.5h 的时候到达 ???? 点.
根据此时接受信号最强,则 ????????⊥???????? ,
又 ????????=30???????? , ????????=50????????
∴ 由勾股定理得 ????????=40????????
∴ 此时,班车到发射塔的距离是40千米.
?
(2)解:连接 BC ,
∵AC=60×2=120km,AM=30km
∴CM=AC-AM=90km
由勾股定理得, BC=1097km
∴1097<100
∴ 故 ???? 城能接到信号.
?
课堂小结:
对称性:既是轴对称图形也是中心对称图形;
等圆或同圆中等弧对等角对等弦;
推论:
点和圆的位置关系:圆内、圆外以及圆上
相关概念:弦、弧、半圆、优弧、劣弧、
圆心角以及圆周角
圆的概念:圆是到定点的距离等于定长的所有的点组成的图形.
圆
谢谢观看
教学内容
1.圆的概念
2.圆的有关概念
4.圆的对称性
圆
3.点和圆的位置关系
1.圆的概念
在平面内,圆是到定点的距离等于定长的所有的点组成的图形.这个定点就是圆心,定长是半径.以点O为圆心的圆,记作⊙O,读作“圆O”.
2.与圆相关的概念
(1)连接圆上任意两点的线段叫做弦,如图①线段AC,AB;
(2)经过圆心的弦叫做直径,如图①线段AB;
(3)圆上任意两点间的部分叫做圆弧,简称弧,“以A、C为端点的弧记作”读作“圆弧AC”或“弧AC”.大于半圆的弧(如图①所示)叫做优弧,小于半圆的弧(如图①所示)或叫做劣弧;
与圆相关的概念
(4)圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆;
(5)能够重合的圆称为等圆;
(6)在同圆或等圆中,能够互相重合的弧,称为等弧
(7)圆心角与圆周角
3.点和圆的位置关系
如图②所示,设⊙O的半径为r,点到圆心的距离为d.
则有:点P在圆外d>r;点P在圆上d=r;点P在圆内d<r.
4.圆的对称性
1.圆是轴对称图形,对称轴是任意一条过圆心直线.
2.圆是中心对称图形,对称中心是圆心.
3.在同圆或等圆中,如果圆心角相等,那么它们所对的弧相等,所对的弦相等.
4.推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中的一组量相等,那么他们对应的其余各组量都分别相等.
运用新知,深化理解
1.判断:
(1)直径是弦.( )
(2)弦是直径.( )
(3)半圆是弧,但弧不一定是半圆.( )
(4)半径相等的两个半圆是等弧.( )
(5)长度相等的两条弧是等弧.( )
(6)周长相等的圆是等圆.( )
(7)面积相等的圆是等圆.( )
(8)优弧一定比劣弧长.( )
√
×
√
√
×
√
√
×
2.如图,半圆的直径AB=________.
3.点A在以O为圆心,3 cm为半径的⊙O内,则点A到圆心O的距离d的范围是________.
解析:根据点和圆的位置关系判定.
答案:0≤d<3.
4.下列说法正确的是( )
A.相等的圆心角所对的弧相等
B.在同圆中,等弧所对的圆心角相等
C.相等的弦所对的圆心到弦的距离相等
D.圆心到弦的距离相等,则弦相等
B
5.如图,AB、AC、BC都是⊙O的弦,∠AOC=∠BOC,∠ABC与∠BAC相等吗?为什么?
解:∵∠AOC=∠BOC,
∴AC=BC.(在同圆或等圆中,如果圆心角相等,那么它们所对的弧相等,所对的弦相等)
∴∠ABC=∠BAC.
随堂练习
1.已知AB是半径为5的圆的一条弦,则AB的长不可能是(?? )
A.?4?????????????????????????B.?8?????????????????C.?10??????????????????????D.?12
2.下列说法①直径是弦②半圆是弧③弦是直径④弧是半圆,其中正确的有(? ?)
3.如图,数轴上有A,B,C三点,点A,C关于点B对称,以原点O为圆心作圆,若点A,B,C分别在 ⊙???? ?外, ⊙???? 内, ⊙???? 上,则原点O的位置应该在(?? )
?
A.?点A与点B之间靠近A点???????????????????????????????????????B.?点A与点B之间靠近B点
C.?点B与点C之间靠近B点????????????????????????????????????????D.?点B与点C之间靠近C点
D
B
C
4.两圆的圆心都是O,半径分别为r1 , r2(r1
5.⊙O的半径为4,圆心O的坐标为(0,0),点P的坐标为(4,2),则点P与⊙O的位置关系是(??? )
A.?点P在⊙O内????????????????B.?点P的⊙O上????????????????C.?点P在⊙O外????????????????D.?点P在⊙O上或⊙O外
6.如图,在网格中(每个小正方形的边长均为1个单位)选取9个格点(格线的交点称为格点).如果以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为(?? )
A.?2 2 <r< 17?????????????????B.?17 <r<3 2???????????????
??C.?17 <r<5?????????????????D.?5<r< 29
?
C
C
B
7.如图,四边形PAOB是扇形OMN的内接矩形,顶点P在 ???????? 上,且不与M、N重合,当P点在 ???????? 上移动时,矩形PAOB的形状,大小随之变化,则AB的长度(?? )
?
A.?不变?????????????B.?变小??????????C.?变大?????????????D.?不能确定
8.如图点A,D,G,B在半圆上,四边形ABOC,DEOF,HMNO均为矩形,设BC=a, EF=b, NH=c,则下列说法正确的是(??? )
A.?a>b>c???????????B.?a=b=c ????????????C.?c>a>b?????????????D.?b>c>a?
A
B
9.在Rt△ABC中 ,∠C=90°,AC=2 , BC=4,若以点C为圆心,AC为半径作圆,则AB边的中点E与⊙C的位置关系为________.
10.已知⊙O的直径是方程 ????2?2?????12=0 的根,且点A到点O的距离是6,则点A与⊙O的位置关系是________.
?
11.如图,在矩形 ???????????????? 中, ????????=3 , ????????=4 ,若以点 ???? 为圆心,以 4 为半径作 ⊙???? ,则点 ???? ,点 ???? ,点 ???? ,点 ???? 四点中在 ⊙???? 外的是________.
?
点E在⊙C外
点A在圆外
点 C
?
12.平面上有⊙O及一点P,P到⊙O上一点的距离最长为6cm,最短为2cm,则⊙O的半径为________cm.
13.爆炸区 50???? 内是危险区,一人在离爆炸中心 ???? 点 30???? 的 ???? 处(如图),这人沿射线________的方向离开最快,离开________ ???? 无危险
?
14.在矩形ABCD中,AB=3,AD=4,以点A为圆心,r为半径画圆,若使点B在⊙A内,点C在⊙A外,则半径r的取值范围是________.
14.3<r<5
20
?
OA
4或2
15.⊙O的半径r=10cm,圆心O到直线l的距离OD=6cm,在直线l上有A、B、C三点,且AD=6cm,BD=8cm,CD=5 3 cm,问:A、B、C三点与⊙O的位置关系各是怎样?
?
解:∵OA= ????????2+????????2 = 62+62 = 72 (cm)<r=10cm,
OB= ????????2+????????2 = 62+82 =10(cm)=r,
OC= ????????2+????????2 = 62+(53)2 = 111 (cm)>r=10cm,
∴点A在⊙O内,点B在⊙O上,点C在⊙O外.
?
16.⊙O的半径r=10cm,圆心O到直线l的距离OD=6cm,在直线l上有A、B、C三点,且AD=6cm,BD=8cm,CD=5 3 cm,问:A、B、C三点与⊙O的位置关系各是怎样?
16.如图,已知AB,CB为⊙O的两条弦,请写出图中所有的弧.
?
图中的弧为 ????????,????????,????????,????????????,????????????,????????????.
?
17.已知:如图,△ABC中, ∠????=90° , ????????=2 ?cm, ????????=4 cm,CM是中线,以C为圆心,以 5 cm长为半径画圆,则点A、B、M与⊙C的关系如何?
?
解:在Rt△ABC中,由勾股定理得,
????????=42+22=25 (cm);
∵ ????????=2 cm <5 cm,
∴点A在⊙O内;
∵ ????????=4 cm >5 cm,
∴点B在⊙C外;
∵ ∠????=90° ,CM斜边上的是中线,
∴ ????????=12????????=5 cm
∴M点在⊙C上.
?
18.在△ABC中,∠C=90°,AC=4,AB=5,以点C为圆心,以r=3为半径作圆,判断A,B两点和⊙C的位置关系.
解:∵∠C=90°,AC=4,AB=5,
∴BC=3.
∵AC=4>r,
∴点A在⊙C外.
∵BC=3=r,
∴点B在⊙C上.
19.以矩形ABCD的顶点A为圆心画⊙A,使得B、C、D中至少有一点在⊙A内,且至少有一点在⊙A外,若BC=12,CD=5.求⊙A的半径r的取值范围。
解:根据题意画图如右,
因为BC=12,CD=5,所以????????=122+52=169=13。若想使得B、C、D中至少有一点在⊙A内,且至少有一点在⊙A外,则第一种情况为:B点在圆内,C、D点在圆外;第二种情况:B、D点在圆内,C点在圆外。综合两种情况来看,5?
20.如图,在直角梯形ABCD中,AD∥BC, ????????=1 , ????????=9 ,M为AB的中点,以CD为直径画圆P.
?
(1)当点M在圆P外时,求CD的长的取值范围;
(2)当点M在圆P上时,求CD的长;
(3)当点M在圆P内时,求CD的长的取值范围.
(1)解:取CD的中点P,连接MP,
∵M为AB的中点,
∴MP是梯形ABCD的中位线.
∵ ????????=1 , ????????=9 ,
∴ ????????=12×(1+9)=5 ,
∵点M在圆P外,
∴ ????????>???????? ,即 2????????>???????? ,
∴ 0?
(2)解:∵点M在圆P上,
∴ ????????=???????? ,即 2????????=???????? ,
∴ ????????=2×5=10
(3)解:∵点M在圆P内,
∴ ????????∴ ????????>10 .
?
21.城市 ???? 的正北方向 50???????? 的 ???? 处,有一无线电信号发射塔.已知,该发射塔发射的无线电信号的有效半径为 100???????? , ???????? 是一条直达 ???? 城的公路,从 ???? 城发往 ???? 城的班车速度为 60????????/h .
?
(1)当班车从 ???? 城出发开往 ???? 城时,某人立即打开无线电收音机,班车行驶了 0.5h 的时候接收信号最强.此时,班车到发射塔的距离是多少千米?(离发射塔越近,信号越强)
(2)班车从 ???? 城到 ???? 城共行驶了 2h ,请你判断到 ???? 城后还能接收到信号吗?请说明理由.
?
(1)解:过点 ???? 作 ????????⊥???????? 于点 ???? ,
设班车行驶了 0.5h 的时候到达 ???? 点.
根据此时接受信号最强,则 ????????⊥???????? ,
又 ????????=30???????? , ????????=50????????
∴ 由勾股定理得 ????????=40????????
∴ 此时,班车到发射塔的距离是40千米.
?
(2)解:连接 BC ,
∵AC=60×2=120km,AM=30km
∴CM=AC-AM=90km
由勾股定理得, BC=1097km
∴1097<100
∴ 故 ???? 城能接到信号.
?
课堂小结:
对称性:既是轴对称图形也是中心对称图形;
等圆或同圆中等弧对等角对等弦;
推论:
点和圆的位置关系:圆内、圆外以及圆上
相关概念:弦、弧、半圆、优弧、劣弧、
圆心角以及圆周角
圆的概念:圆是到定点的距离等于定长的所有的点组成的图形.
圆
谢谢观看
