北师大版数学七年级下册1.2《幂的乘方与积的乘方(第1课时)幂的乘方》课件(共22张PPT)
文档属性
| 名称 | 北师大版数学七年级下册1.2《幂的乘方与积的乘方(第1课时)幂的乘方》课件(共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 381.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-19 08:39:19 | ||
图片预览








文档简介
1.乙正方体的棱长是2cm,则乙正方体的体积V=______.甲正方体的棱长是乙正方体的5倍,则甲正方体的体积V=______。
2.乙球的半径为3cm,则乙球的体积V=________甲球的半径是乙球的10倍,则甲球的体积V甲=______cm3。
2.幂的乘方与积的乘方
第1课时 幂的乘方
1. 经历探索幂的乘方的运算法则的过程,进一步体会幂的意义.
2.了解幂的乘方的运算法则,并能解决一些实际问题.
学习目标
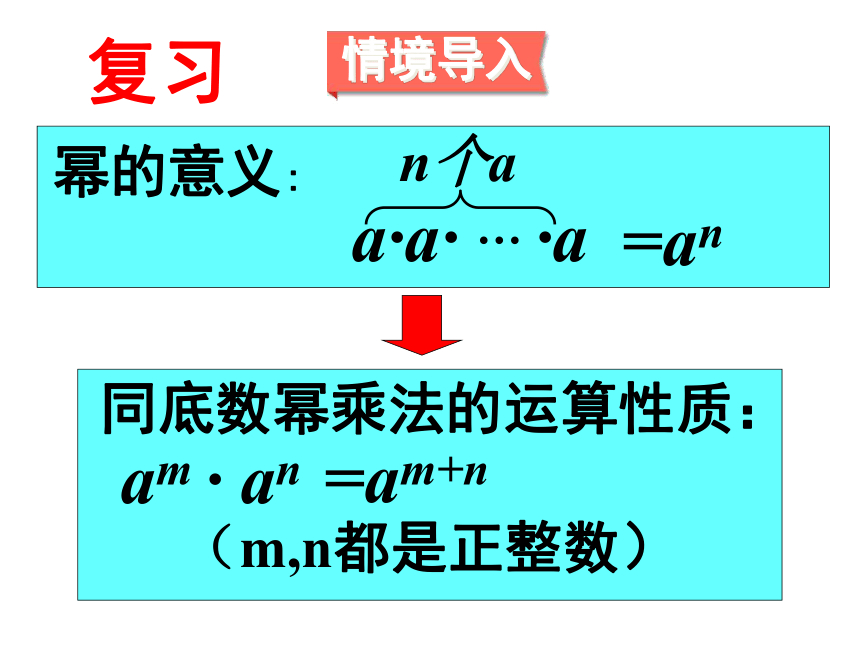
复习
幂的意义:
a·a· … ·a
n个a
=an
同底数幂乘法的运算性质:
am · an
=am+n
(m,n都是正整数)
情境导入
地球、木星、太阳可以近似地看作球体 .木星、太阳的半径分别约是地球的10倍和102倍,它们的体积分别约是地球的 倍和 倍!那么你知道 等于多少吗?
103
(102)3
(102)3
(102)3
=102×102×102
=102+2+2
=102×3
=106
太棒了!
(根据 ).
(根据 ).
同底数幂的乘法性质
幂的意义
探索新知
做一做
计算下列各式,并说明理由
(am)n
=am·am· … ·am
n个am
=am+m+ … +m
n个m
=amn
(幂的意义)
(同底数幂的乘法)
(乘法的意义)
幂的乘方法则:
这就是说:
幂的乘方,底数不变,
指数相乘。
其中m , n都是正整数
(1)(102)3 ; (2) (b5)5 ; (3) (an)3; (4) -(x2)m ; (5) (y2)3 · y ; (6) 2(a2)6 – (a3)4 .
例1计算:
练一练
计算:
(1)(103)3 ; (2) –(a2)5 ;
(3) (x3)4 · x2 ; (4) [(-x)2 ]3 ;
(5) (-a)2(a2)2 ; (6) x·x4 – x2 · x3 .
2. 判断下面计算是否正确?如果有错误请改正:
想一想:同底数幂的乘法法则与幂的乘方法则有什么相同点和不同点?
幂的乘方法则:
(其中m,n都是正整数)
同底数幂的乘法法则:
底数不变
指数相乘
指数相加
同底数幂相乘
幂的乘方
其中m,n都是正整数
底数不变
思考题:
1、若 am = 2,
则 a3m =____.
2、若 mx = 2, my = 3 ,
则 mx+y =___,
m3x+2y =___.
8
6
72
动脑筋!
随堂演练
小结
Ⅰ.幂的乘方法则:
Ⅱ.请特别注意同底数幂的乘法法则与幂的乘方法则的区别.
小结
同底数幂乘法的运算性质:
am·an=am+n(m,n都是正整数)
底数 ,
指数 .
幂的乘方的运算性质:
(am)n = amn (m,n 都是正整数).
底数 ,
指数 .
相加
相乘
不变
不变
幂的意义
在255,344,433,522这四个幂中,数值最大的一个是———。
344
课堂作业:
课本P6页,习题1.2
第1、2 题.
2.乙球的半径为3cm,则乙球的体积V=________甲球的半径是乙球的10倍,则甲球的体积V甲=______cm3。
2.幂的乘方与积的乘方
第1课时 幂的乘方
1. 经历探索幂的乘方的运算法则的过程,进一步体会幂的意义.
2.了解幂的乘方的运算法则,并能解决一些实际问题.
学习目标
复习
幂的意义:
a·a· … ·a
n个a
=an
同底数幂乘法的运算性质:
am · an
=am+n
(m,n都是正整数)
情境导入
地球、木星、太阳可以近似地看作球体 .木星、太阳的半径分别约是地球的10倍和102倍,它们的体积分别约是地球的 倍和 倍!那么你知道 等于多少吗?
103
(102)3
(102)3
(102)3
=102×102×102
=102+2+2
=102×3
=106
太棒了!
(根据 ).
(根据 ).
同底数幂的乘法性质
幂的意义
探索新知
做一做
计算下列各式,并说明理由
(am)n
=am·am· … ·am
n个am
=am+m+ … +m
n个m
=amn
(幂的意义)
(同底数幂的乘法)
(乘法的意义)
幂的乘方法则:
这就是说:
幂的乘方,底数不变,
指数相乘。
其中m , n都是正整数
(1)(102)3 ; (2) (b5)5 ; (3) (an)3; (4) -(x2)m ; (5) (y2)3 · y ; (6) 2(a2)6 – (a3)4 .
例1计算:
练一练
计算:
(1)(103)3 ; (2) –(a2)5 ;
(3) (x3)4 · x2 ; (4) [(-x)2 ]3 ;
(5) (-a)2(a2)2 ; (6) x·x4 – x2 · x3 .
2. 判断下面计算是否正确?如果有错误请改正:
想一想:同底数幂的乘法法则与幂的乘方法则有什么相同点和不同点?
幂的乘方法则:
(其中m,n都是正整数)
同底数幂的乘法法则:
底数不变
指数相乘
指数相加
同底数幂相乘
幂的乘方
其中m,n都是正整数
底数不变
思考题:
1、若 am = 2,
则 a3m =____.
2、若 mx = 2, my = 3 ,
则 mx+y =___,
m3x+2y =___.
8
6
72
动脑筋!
随堂演练
小结
Ⅰ.幂的乘方法则:
Ⅱ.请特别注意同底数幂的乘法法则与幂的乘方法则的区别.
小结
同底数幂乘法的运算性质:
am·an=am+n(m,n都是正整数)
底数 ,
指数 .
幂的乘方的运算性质:
(am)n = amn (m,n 都是正整数).
底数 ,
指数 .
相加
相乘
不变
不变
幂的意义
在255,344,433,522这四个幂中,数值最大的一个是———。
344
课堂作业:
课本P6页,习题1.2
第1、2 题.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
