4.3利用“边边边”判定三角形全等(1)-北师大版七年级下册数学课件 (共36张PPT)
文档属性
| 名称 | 4.3利用“边边边”判定三角形全等(1)-北师大版七年级下册数学课件 (共36张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 566.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-19 00:00:00 | ||
图片预览






文档简介
探索三角形全等
的条件
1.掌握三角形全等的“SSS”判定,并能应用它判别两个三
角形是否全等,以及运用该条件解决一些简单的实际
问题;(重点)
2.了解三角形的稳定性,以及这一性质在生活中的实际
应用;
3.由探索三角形全等条件的过程,体会由操作、归纳获
得数学结论的过程.(难点)
学习目标
如图,
A
B
C
E
F
G
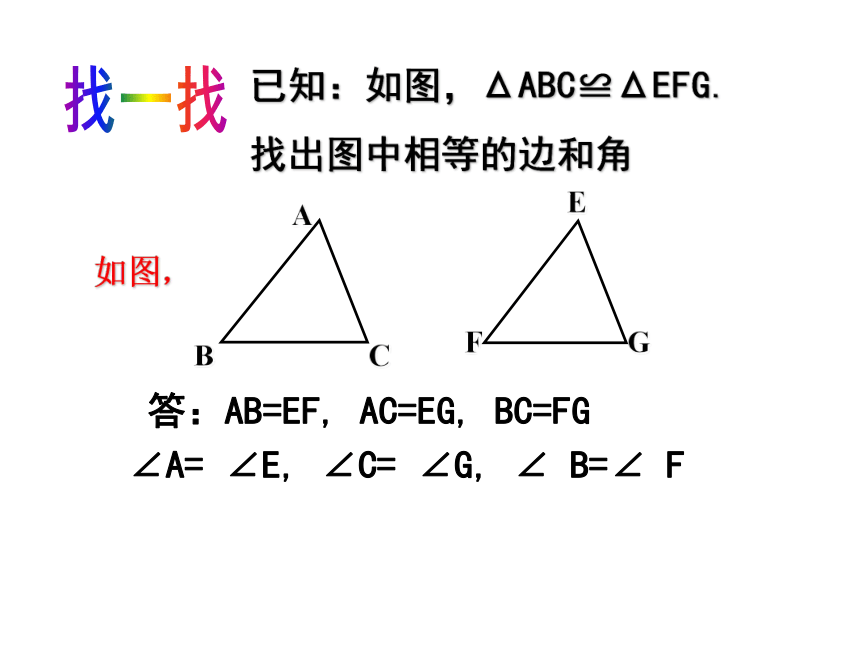
已知:如图,ΔABC≌ΔEFG.
找出图中相等的边和角
答:AB=EF, AC=EG, BC=FG
∠A= ∠E, ∠C= ∠G, ∠ B=∠ F
找一找
小颖作业本上画的三角形被墨迹污染了,她想画一个与原来完全一样的三角形,她该怎么办?请你帮助小颖想一个办法,并说明你的理由?
注意:与原来完全一样的三角形,即是与原来三角形全等的三角形.
问题引入
要画一个三角形与小颖画的三角形全等。需要几个与边或角的大小有关的条件?只知道一个条件行吗?两个条件呢?三个条件呢?
让我们一起来探索三角形全等的条件
想一想
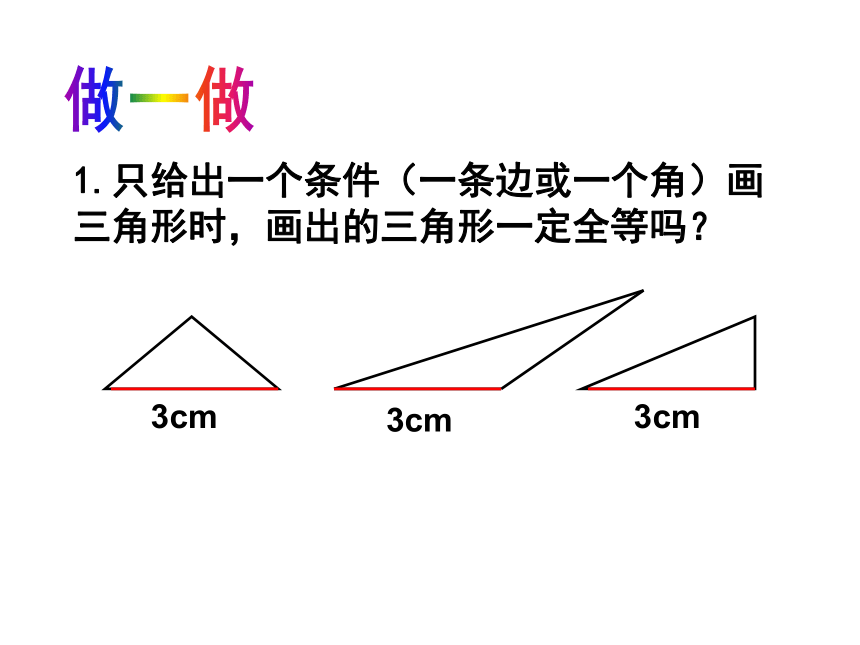
1.只给出一个条件(一条边或一个角)画三角形时,画出的三角形一定全等吗?
3cm
3cm
3cm
做一做
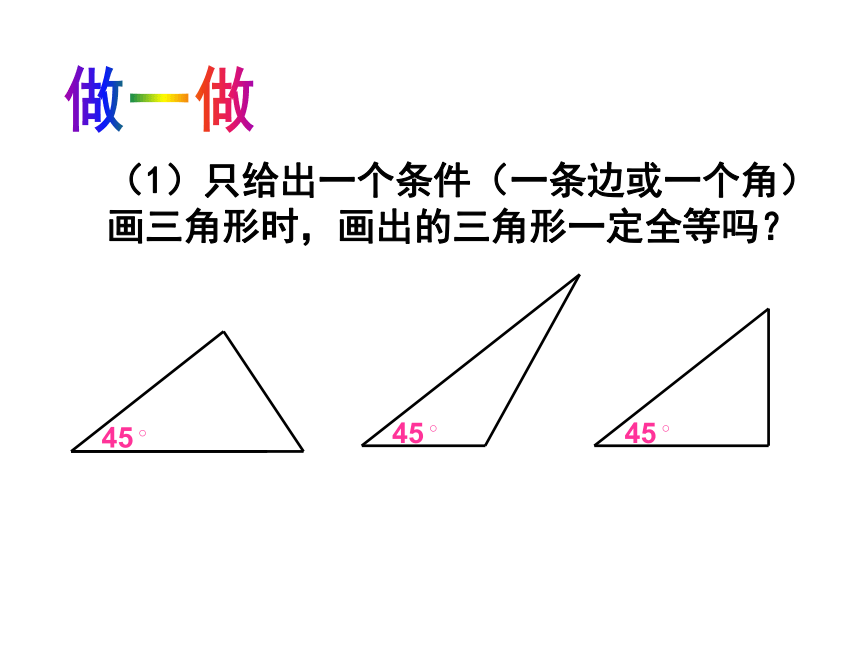
(1)只给出一个条件(一条边或一个角)画三角形时,画出的三角形一定全等吗?
45?
45?
45?
做一做
1)三角形的一个内角、一条边分别相等;
2)三角形的两个内角分别相等;
3)三角形的两条边分别相等.
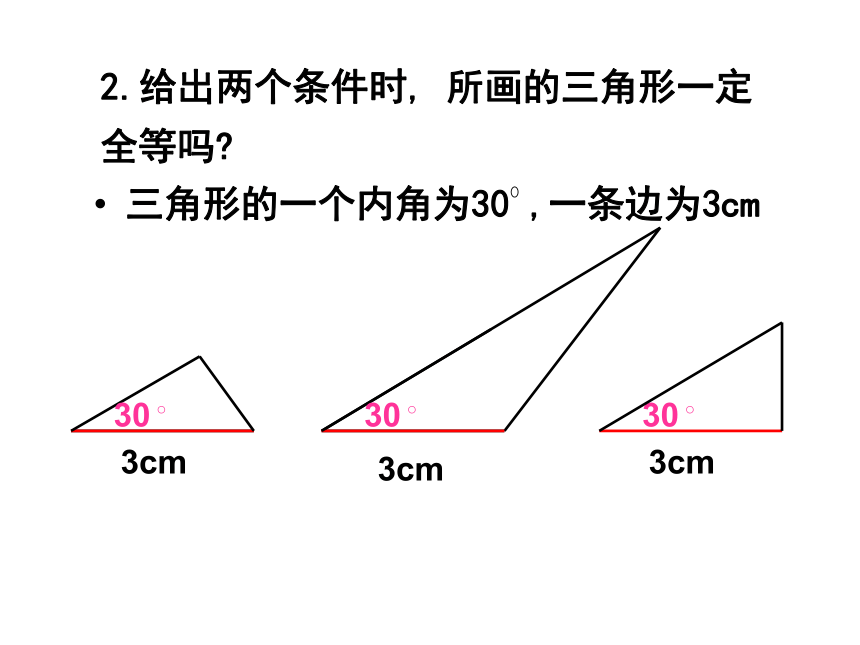
2.给出两个条件画三角形时,有几种可能的情况?每种情况下作出的三角形一定全等吗?
三角形的一个内角为30 ,一条边为3cm
30?
3cm
3cm
3cm
30?
30?
2.给出两个条件时, 所画的三角形一定全等吗?
30?
30?
50?
50?
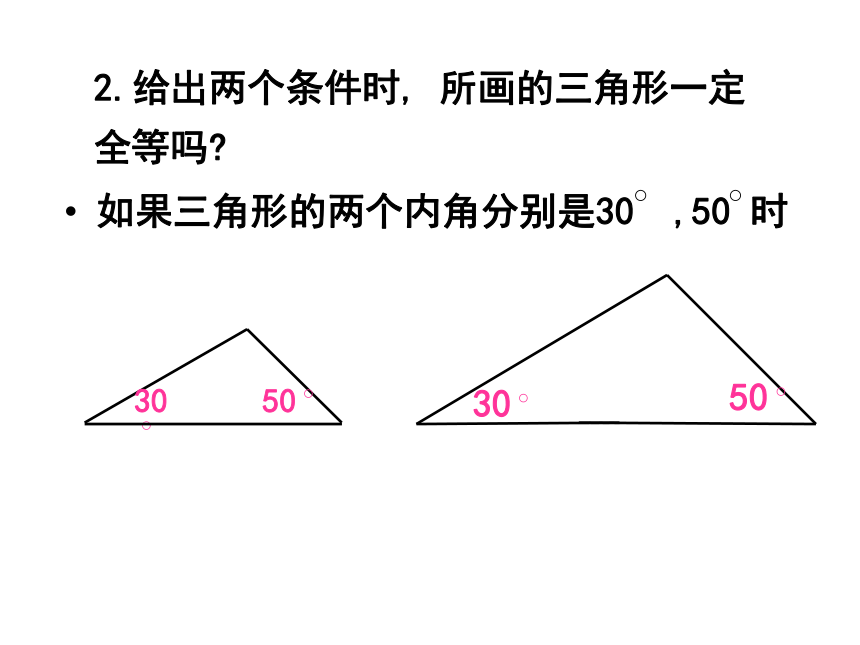
2.给出两个条件时, 所画的三角形一定全等吗?
如果三角形的两个内角分别是30 ,50 时
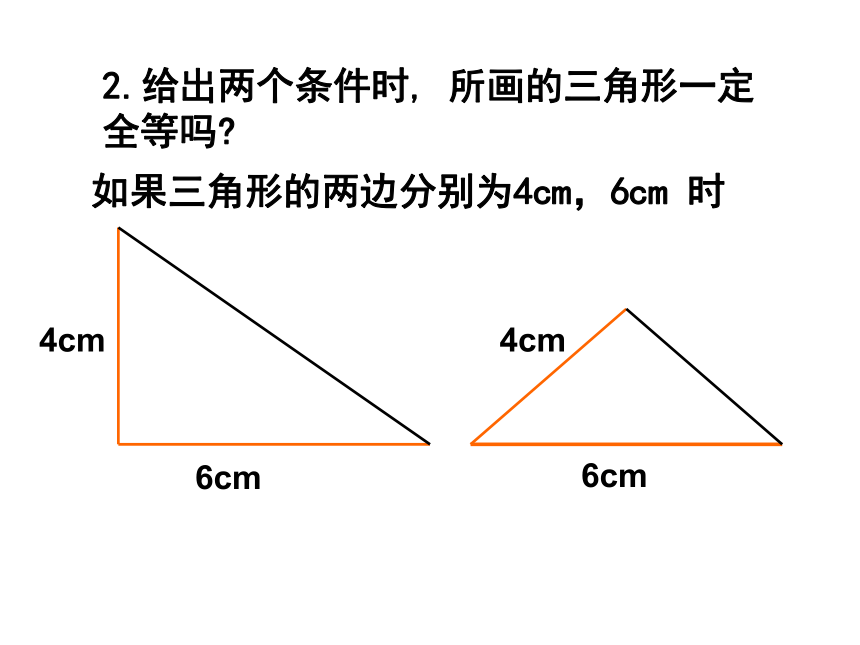
2.给出两个条件时, 所画的三角形一定全等吗?
如果三角形的两边分别为4cm,6cm 时
6cm
6cm
4cm
4cm
只给出一个条件或两个条件时,
都不能保证所画出的三角形全等。
结论:
若给出三个条件画三角形,你能说出有哪几种可能情况?
都给角:给三个角
2.都给边:给三条边
3.既给角,又给边:
(1)给一条边,两个角
(2)给两条边,一个角
议一议
已知一个三角形的三个内角 分别为400,600,800,请画出这个三角形。
结论:三个内角对应相等的两个三角形不一定全等.
1.给出三个角
做一做
已知三角形的三条边分别为4cm、5cm和7cm,请画出这个三角形。
三边对应相等的两个三角形全等,简写为“边边边”或“SSS”
边边边公理:
2.给出三条边
做一做
三边对应相等的两个三角形全等,简写为“边边边”或“SSS”。
用法
A
B
C
D
E
F
在△ABC和△DEF中
∵
AB=DE
BC=EF
AC=DF
∴ △ABC≌△DEF(SSS)
导入新课
观察与思考
拿三根火柴棍搭三角形,你能搭出几种呢?试试看.
只能搭出唯一三角形
讲授新课
“SSS”判定三角形全等及三角形的稳定性
一
已知两个三角形的三条边都分别为3cm、4cm、6cm .它们一定全等吗?
3cm
4cm
6cm
4cm
6cm
3cm
6cm
4cm
3cm
结论: 三边对应相等的两个三角形全等(可以简写为“边边边”或“SSS”)
A
B
C
D
E
F
在△ABC和△ DEF中,
∴ △ABC ≌△ DEF(SSS).
AB=DE,
BC=EF,
CA=FD,
用符号语言表达为:
这个定理说明,只要三角形的三边的长度确定了,这个三角形的形状和大小就完全确定了,这也是三角形具有稳定性的原理.
三角形的大小和形状是固定不变的,而四边形的形状会改变.
A
C
B
D
证明:∵D是BC的中点,
∴BD=CD.
在△ABD与△ACD中,
AB=AC(已知),
BD=CD(已证),
AD=AD(公共边),
∴△ABD≌△ACD(SSS),
如图, △ABC是一个钢架,AB=AC,AD是连接A与BC中点D的支架,求证:
∠B=∠C.
∴∠B=∠C.
“SSS”的判定与性质的综合运用
二
例1 如图,当 AB=CD,BC=DA时,图中的△ABC与△CDA是否全等?并说明理由。
答:△ABC与△CDA是全等三角形。
证明:
在△ABC与△CDA中
∴△ABC≌△CDA
(SSS)
∵
AB=CD
AD=CB
AC=CA
(已知)
(已知)
(公共边)
例题赏析
答:能判定AB∥CD.
变式:如图,当 AB=CD,BC=DA时,你能说明AB与CD、AD与BC的位置关系吗?为什么?
1
2
3
4
举一反三
∴∠3=∠4,∠1=∠2
(全等三角形对应角相等)
∴AB∥CD,AD∥BC
(内错角相等,两直线平行)
证明:
在△ABC与△CDA中
∴△ABC≌△CDA
(SSS)
∵
AB=CD
AD=CB
AC=CA
(已知)
(已知)
(公共边)
1
2
3
4
举一反三
两个锐角对应相等的两个直角三角形全等吗?为什么?
答:不一定全等
比如右边的两图,满足上述条件,但不全等
练一练
2.已知:AC、BD相交于点O,且AB=DC,AC=DB,那么∠A=∠D吗?为什么?
答: 我认为:∠A=∠D
证明:
在△ABC和△DCB中
∵
∴△ABC≌△DCB(SSS)
∴∠A=∠D(全等三角形的对应角相等)
准备若干长度适中的小木条,用其中三根木条钉成一个三角形的框架,它的形状和大小是固定的吗?如果用四根小木条钉成的框架形状和大小固定吗?
三角形的框架,它的大小和形状是固定不变的,三角形的这个性质叫做三角形的稳定性。
动手做一做
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
观察下图,这些图形的设计原理是什么?
你还能举出一些其他的例子吗?
只给出一个条件或两个条件时,都不能保证两个三角形全等。
三个内角对应相等的两个三角形不一定全等。
边边边公理:三边对应相等的两个三角形全等,简写为“边边边”或“SSS”。
三角形具有稳定性。
1.通过这节课的学习活动你有哪些收获?
你还有什么想法吗?
感悟与反思
1. 如图,AB=AC, BD=CD, BH=CH. 图中有几组全等的三角形?它们全等的条件是什么?
解: 在△ABH和△ACH中
同理 △ABD≌△ACD
△DBH≌△DCH
( SSS)
∴△ABH≌△ACH
∵
达标测试
四边形不具有稳定性,人们往往通过改造,将其变成三角形从而增强其稳定性
盖房子时,在窗框未安装好之前,木工师傅常常在窗框上斜定一根木条。为什么要这样做呢?
三边分别相等的两个三角形
三角形全等的“SSS”判定:三边分别相等的两个三角形全等.
课堂小结
三角形的稳定性:三角形三边长度确定了,这个三角形的形状和大小就完全确定了.
的条件
1.掌握三角形全等的“SSS”判定,并能应用它判别两个三
角形是否全等,以及运用该条件解决一些简单的实际
问题;(重点)
2.了解三角形的稳定性,以及这一性质在生活中的实际
应用;
3.由探索三角形全等条件的过程,体会由操作、归纳获
得数学结论的过程.(难点)
学习目标
如图,
A
B
C
E
F
G
已知:如图,ΔABC≌ΔEFG.
找出图中相等的边和角
答:AB=EF, AC=EG, BC=FG
∠A= ∠E, ∠C= ∠G, ∠ B=∠ F
找一找
小颖作业本上画的三角形被墨迹污染了,她想画一个与原来完全一样的三角形,她该怎么办?请你帮助小颖想一个办法,并说明你的理由?
注意:与原来完全一样的三角形,即是与原来三角形全等的三角形.
问题引入
要画一个三角形与小颖画的三角形全等。需要几个与边或角的大小有关的条件?只知道一个条件行吗?两个条件呢?三个条件呢?
让我们一起来探索三角形全等的条件
想一想
1.只给出一个条件(一条边或一个角)画三角形时,画出的三角形一定全等吗?
3cm
3cm
3cm
做一做
(1)只给出一个条件(一条边或一个角)画三角形时,画出的三角形一定全等吗?
45?
45?
45?
做一做
1)三角形的一个内角、一条边分别相等;
2)三角形的两个内角分别相等;
3)三角形的两条边分别相等.
2.给出两个条件画三角形时,有几种可能的情况?每种情况下作出的三角形一定全等吗?
三角形的一个内角为30 ,一条边为3cm
30?
3cm
3cm
3cm
30?
30?
2.给出两个条件时, 所画的三角形一定全等吗?
30?
30?
50?
50?
2.给出两个条件时, 所画的三角形一定全等吗?
如果三角形的两个内角分别是30 ,50 时
2.给出两个条件时, 所画的三角形一定全等吗?
如果三角形的两边分别为4cm,6cm 时
6cm
6cm
4cm
4cm
只给出一个条件或两个条件时,
都不能保证所画出的三角形全等。
结论:
若给出三个条件画三角形,你能说出有哪几种可能情况?
都给角:给三个角
2.都给边:给三条边
3.既给角,又给边:
(1)给一条边,两个角
(2)给两条边,一个角
议一议
已知一个三角形的三个内角 分别为400,600,800,请画出这个三角形。
结论:三个内角对应相等的两个三角形不一定全等.
1.给出三个角
做一做
已知三角形的三条边分别为4cm、5cm和7cm,请画出这个三角形。
三边对应相等的两个三角形全等,简写为“边边边”或“SSS”
边边边公理:
2.给出三条边
做一做
三边对应相等的两个三角形全等,简写为“边边边”或“SSS”。
用法
A
B
C
D
E
F
在△ABC和△DEF中
∵
AB=DE
BC=EF
AC=DF
∴ △ABC≌△DEF(SSS)
导入新课
观察与思考
拿三根火柴棍搭三角形,你能搭出几种呢?试试看.
只能搭出唯一三角形
讲授新课
“SSS”判定三角形全等及三角形的稳定性
一
已知两个三角形的三条边都分别为3cm、4cm、6cm .它们一定全等吗?
3cm
4cm
6cm
4cm
6cm
3cm
6cm
4cm
3cm
结论: 三边对应相等的两个三角形全等(可以简写为“边边边”或“SSS”)
A
B
C
D
E
F
在△ABC和△ DEF中,
∴ △ABC ≌△ DEF(SSS).
AB=DE,
BC=EF,
CA=FD,
用符号语言表达为:
这个定理说明,只要三角形的三边的长度确定了,这个三角形的形状和大小就完全确定了,这也是三角形具有稳定性的原理.
三角形的大小和形状是固定不变的,而四边形的形状会改变.
A
C
B
D
证明:∵D是BC的中点,
∴BD=CD.
在△ABD与△ACD中,
AB=AC(已知),
BD=CD(已证),
AD=AD(公共边),
∴△ABD≌△ACD(SSS),
如图, △ABC是一个钢架,AB=AC,AD是连接A与BC中点D的支架,求证:
∠B=∠C.
∴∠B=∠C.
“SSS”的判定与性质的综合运用
二
例1 如图,当 AB=CD,BC=DA时,图中的△ABC与△CDA是否全等?并说明理由。
答:△ABC与△CDA是全等三角形。
证明:
在△ABC与△CDA中
∴△ABC≌△CDA
(SSS)
∵
AB=CD
AD=CB
AC=CA
(已知)
(已知)
(公共边)
例题赏析
答:能判定AB∥CD.
变式:如图,当 AB=CD,BC=DA时,你能说明AB与CD、AD与BC的位置关系吗?为什么?
1
2
3
4
举一反三
∴∠3=∠4,∠1=∠2
(全等三角形对应角相等)
∴AB∥CD,AD∥BC
(内错角相等,两直线平行)
证明:
在△ABC与△CDA中
∴△ABC≌△CDA
(SSS)
∵
AB=CD
AD=CB
AC=CA
(已知)
(已知)
(公共边)
1
2
3
4
举一反三
两个锐角对应相等的两个直角三角形全等吗?为什么?
答:不一定全等
比如右边的两图,满足上述条件,但不全等
练一练
2.已知:AC、BD相交于点O,且AB=DC,AC=DB,那么∠A=∠D吗?为什么?
答: 我认为:∠A=∠D
证明:
在△ABC和△DCB中
∵
∴△ABC≌△DCB(SSS)
∴∠A=∠D(全等三角形的对应角相等)
准备若干长度适中的小木条,用其中三根木条钉成一个三角形的框架,它的形状和大小是固定的吗?如果用四根小木条钉成的框架形状和大小固定吗?
三角形的框架,它的大小和形状是固定不变的,三角形的这个性质叫做三角形的稳定性。
动手做一做
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
观察下图,这些图形的设计原理是什么?
你还能举出一些其他的例子吗?
只给出一个条件或两个条件时,都不能保证两个三角形全等。
三个内角对应相等的两个三角形不一定全等。
边边边公理:三边对应相等的两个三角形全等,简写为“边边边”或“SSS”。
三角形具有稳定性。
1.通过这节课的学习活动你有哪些收获?
你还有什么想法吗?
感悟与反思
1. 如图,AB=AC, BD=CD, BH=CH. 图中有几组全等的三角形?它们全等的条件是什么?
解: 在△ABH和△ACH中
同理 △ABD≌△ACD
△DBH≌△DCH
( SSS)
∴△ABH≌△ACH
∵
达标测试
四边形不具有稳定性,人们往往通过改造,将其变成三角形从而增强其稳定性
盖房子时,在窗框未安装好之前,木工师傅常常在窗框上斜定一根木条。为什么要这样做呢?
三边分别相等的两个三角形
三角形全等的“SSS”判定:三边分别相等的两个三角形全等.
课堂小结
三角形的稳定性:三角形三边长度确定了,这个三角形的形状和大小就完全确定了.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
