_高中数学人教A版必修一率三章3.1.1方程的根和函数的零点(公开课)课件(共14张PPT)
文档属性
| 名称 | _高中数学人教A版必修一率三章3.1.1方程的根和函数的零点(公开课)课件(共14张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 403.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-19 00:00:00 | ||
图片预览


文档简介
人教A版必修1
第三章 函数的应用
3.1.1 方程的根与函数的零点
问题·探索
问题:判断下面方程是否有实根,有几个实根?
x2- 2x- 3=0
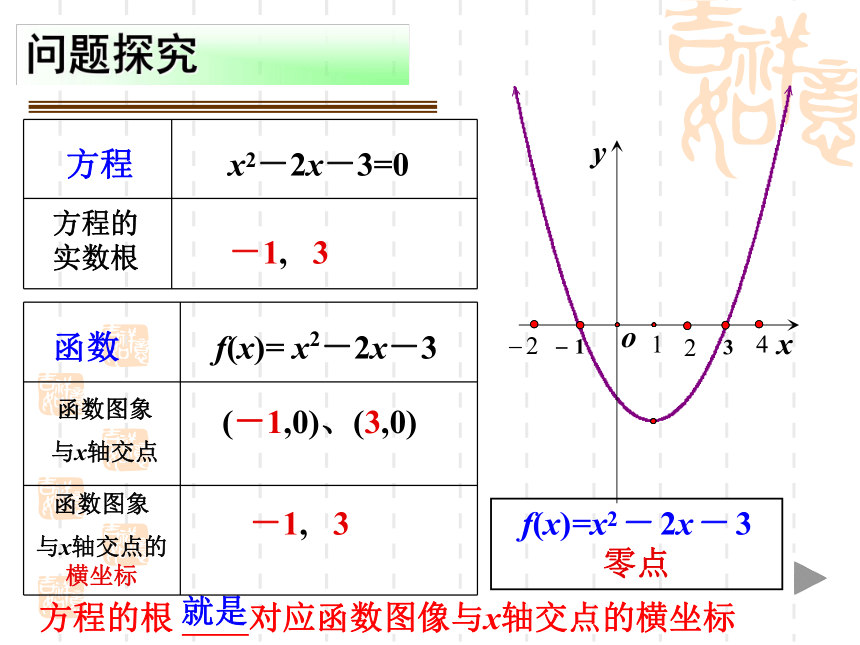
问题探究
x
y
o
方程
x2-2x-3=0
方程的
实数根
-1, 3
函数
f(x)= x2-2x-3
(-1,0)、(3,0)
方程的根 对应函数图像与x轴交点的横坐标
就是
函数图象
与x轴交点
函数图象
与x轴交点的横坐标
-1, 3
f(x)=x2- 2x- 3 零点
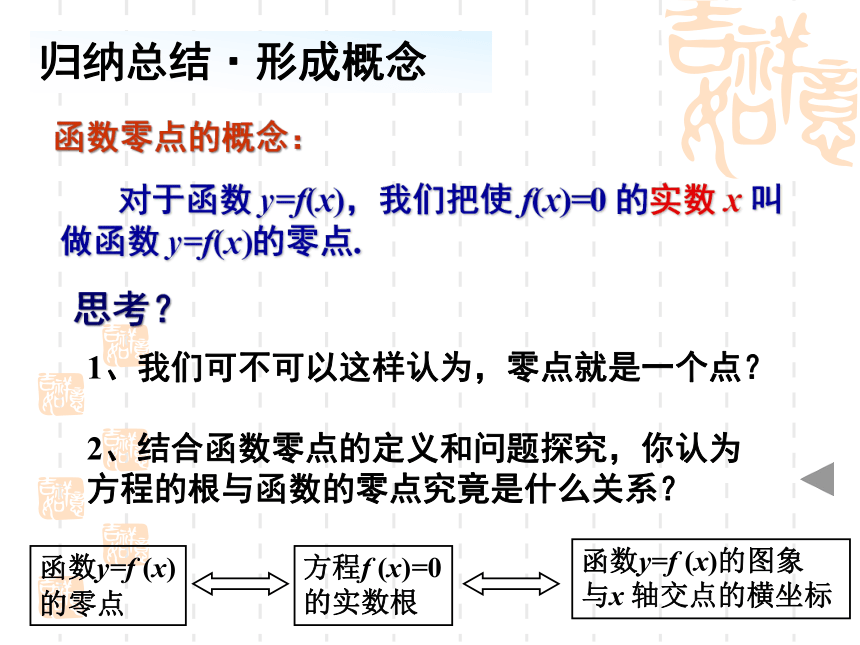
函数零点的概念:
对于函数 y=f(x),我们把使 f(x)=0 的实数 x 叫做函数 y=f(x)的零点.
思考?
1、我们可不可以这样认为,零点就是一个点?
2、结合函数零点的定义和问题探究,你认为方程的根与函数的零点究竟是什么关系?
归纳总结·形成概念
方程f (x)=0
的实数根
函数y=f (x)的图象
与x 轴交点的横坐标
函数y=f (x)
的零点
5
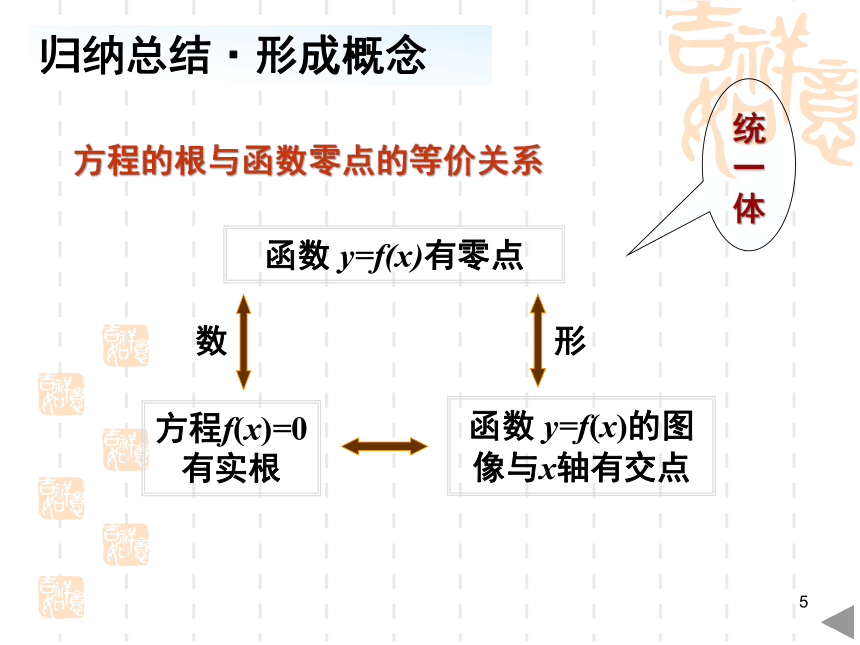
函数 y=f(x)有零点
方程的根与函数零点的等价关系
方程f(x)=0有实根
函数 y=f(x)的图像与x轴有交点
数
形
统一体
归纳总结·形成概念
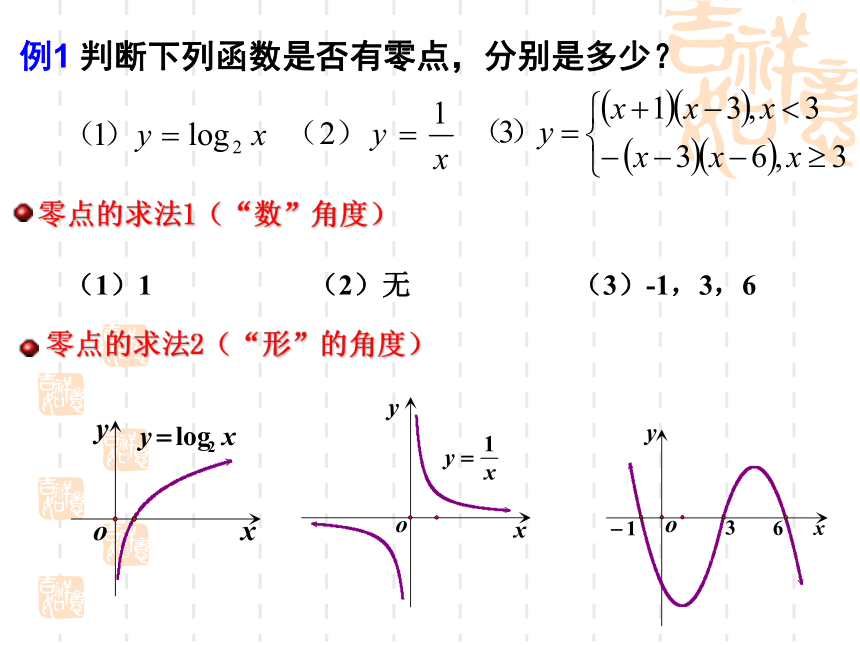
例1 判断下列函数是否有零点,分别是多少?
零点的求法2(“形”的角度)
零点的求法1(“数”角度)
(1)1
(2)无
(3)-1,3,6
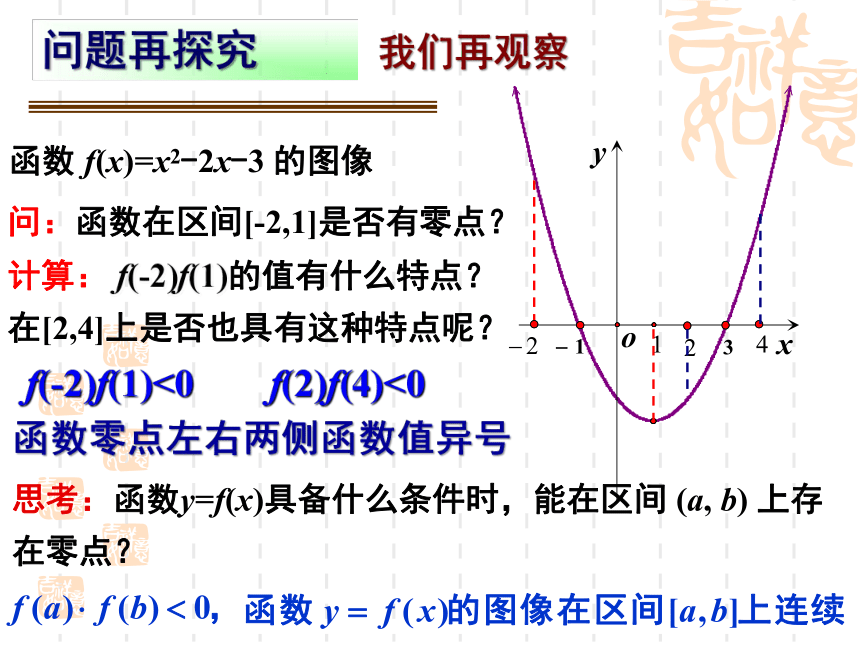
问题再探究
我们再观察
函数 f(x)=x2-2x-3 的图像
函数零点左右两侧函数值异号
问:函数在区间[-2,1]是否有零点?
计算: f(-2)f(1)的值有什么特点?在[2,4]上是否也具有这种特点呢?
x
y
o
思考:函数y=f(x)具备什么条件时,能在区间 (a, b) 上存在零点?
f(-2)f(1)<0
f(2)f(4)<0
零点存在性定理
如果函数 y=f(x) 在区间[a,b]上的图象是连续不断的一条曲线,并且有 f(a)?f(b)<0,那么,函数 y=f(x) 在区间(a, b)内有零点.
即存在c∈(a, b),使得 f(c)=0,这个c 也就是方程 f(x)=0 的根.
建构数学
定理理解
思考1 若只给条件f(a) · f(b)<0能否保证在(a,b)有零点?
注1:函数y=f(x)在(a,b)存在零点必须同时满足:
(1)函数在[a,b]连续;
(2)f(a)·f(b) <0.
定理理解
思考2 如果函数y=f(x)在区间[a,b]上的图象是连续不断曲线,那么当f(a)·f(b)>0时,y=f(x)在区间(a,b)内一定没有零点吗?
注2:若f(x)在区间[a,b]连续且f(a)·f(b)>0,则f(x)在(a,b)也可能有零点.
定理理解
思考3 满足定理条件的零点唯一吗?什么情况零点唯一?
注3:(1)定理只能判断存在性,不能确定有多少个零点;
(2)若f(x)是单调函数,并在区间[a,b]连续且f(a)·f(b)<0,则f(x)在(a,b)有唯一零点.
说明函数在区间(e-1,e)内有零点.
根据函数单调性的性质可知函数f(x)=lnx+2x-6在定义域(0,+∞)内是增函数.
例2讨论f(x)=lnx+2x-6在区间[e-1,e]上零点的存在性及个数.
应用与实践
下面给出证明:任取x1、x2>0,不妨x1因此,f(x)=lnx+2x-6在[e-1,e]仅有一个零点.
练习 在下列哪个区间内,函数f(x)= x3+x-2
一定有零点( )
A.(-1,0) B.(0,2) C.(1,2) D.(2,3)
B
1.知识方面
零点的概念
方程的根与函数零点的等价关系
零点存在性定理
2.数学思想方面
函数与方程思想
化归转化思想
数形结合思想
第三章 函数的应用
3.1.1 方程的根与函数的零点
问题·探索
问题:判断下面方程是否有实根,有几个实根?
x2- 2x- 3=0
问题探究
x
y
o
方程
x2-2x-3=0
方程的
实数根
-1, 3
函数
f(x)= x2-2x-3
(-1,0)、(3,0)
方程的根 对应函数图像与x轴交点的横坐标
就是
函数图象
与x轴交点
函数图象
与x轴交点的横坐标
-1, 3
f(x)=x2- 2x- 3 零点
函数零点的概念:
对于函数 y=f(x),我们把使 f(x)=0 的实数 x 叫做函数 y=f(x)的零点.
思考?
1、我们可不可以这样认为,零点就是一个点?
2、结合函数零点的定义和问题探究,你认为方程的根与函数的零点究竟是什么关系?
归纳总结·形成概念
方程f (x)=0
的实数根
函数y=f (x)的图象
与x 轴交点的横坐标
函数y=f (x)
的零点
5
函数 y=f(x)有零点
方程的根与函数零点的等价关系
方程f(x)=0有实根
函数 y=f(x)的图像与x轴有交点
数
形
统一体
归纳总结·形成概念
例1 判断下列函数是否有零点,分别是多少?
零点的求法2(“形”的角度)
零点的求法1(“数”角度)
(1)1
(2)无
(3)-1,3,6
问题再探究
我们再观察
函数 f(x)=x2-2x-3 的图像
函数零点左右两侧函数值异号
问:函数在区间[-2,1]是否有零点?
计算: f(-2)f(1)的值有什么特点?在[2,4]上是否也具有这种特点呢?
x
y
o
思考:函数y=f(x)具备什么条件时,能在区间 (a, b) 上存在零点?
f(-2)f(1)<0
f(2)f(4)<0
零点存在性定理
如果函数 y=f(x) 在区间[a,b]上的图象是连续不断的一条曲线,并且有 f(a)?f(b)<0,那么,函数 y=f(x) 在区间(a, b)内有零点.
即存在c∈(a, b),使得 f(c)=0,这个c 也就是方程 f(x)=0 的根.
建构数学
定理理解
思考1 若只给条件f(a) · f(b)<0能否保证在(a,b)有零点?
注1:函数y=f(x)在(a,b)存在零点必须同时满足:
(1)函数在[a,b]连续;
(2)f(a)·f(b) <0.
定理理解
思考2 如果函数y=f(x)在区间[a,b]上的图象是连续不断曲线,那么当f(a)·f(b)>0时,y=f(x)在区间(a,b)内一定没有零点吗?
注2:若f(x)在区间[a,b]连续且f(a)·f(b)>0,则f(x)在(a,b)也可能有零点.
定理理解
思考3 满足定理条件的零点唯一吗?什么情况零点唯一?
注3:(1)定理只能判断存在性,不能确定有多少个零点;
(2)若f(x)是单调函数,并在区间[a,b]连续且f(a)·f(b)<0,则f(x)在(a,b)有唯一零点.
说明函数在区间(e-1,e)内有零点.
根据函数单调性的性质可知函数f(x)=lnx+2x-6在定义域(0,+∞)内是增函数.
例2讨论f(x)=lnx+2x-6在区间[e-1,e]上零点的存在性及个数.
应用与实践
下面给出证明:任取x1、x2>0,不妨x1
练习 在下列哪个区间内,函数f(x)= x3+x-2
一定有零点( )
A.(-1,0) B.(0,2) C.(1,2) D.(2,3)
B
1.知识方面
零点的概念
方程的根与函数零点的等价关系
零点存在性定理
2.数学思想方面
函数与方程思想
化归转化思想
数形结合思想
