高二数学人教B版(2019)选择性必修第一册第二章2.2.3两条直线的位置关系 课件(共15张PPT)
文档属性
| 名称 | 高二数学人教B版(2019)选择性必修第一册第二章2.2.3两条直线的位置关系 课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 307.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-19 00:00:00 | ||
图片预览





文档简介
2.2.3 两条直线的位置关系
时间:2020年11月4日
主讲人:
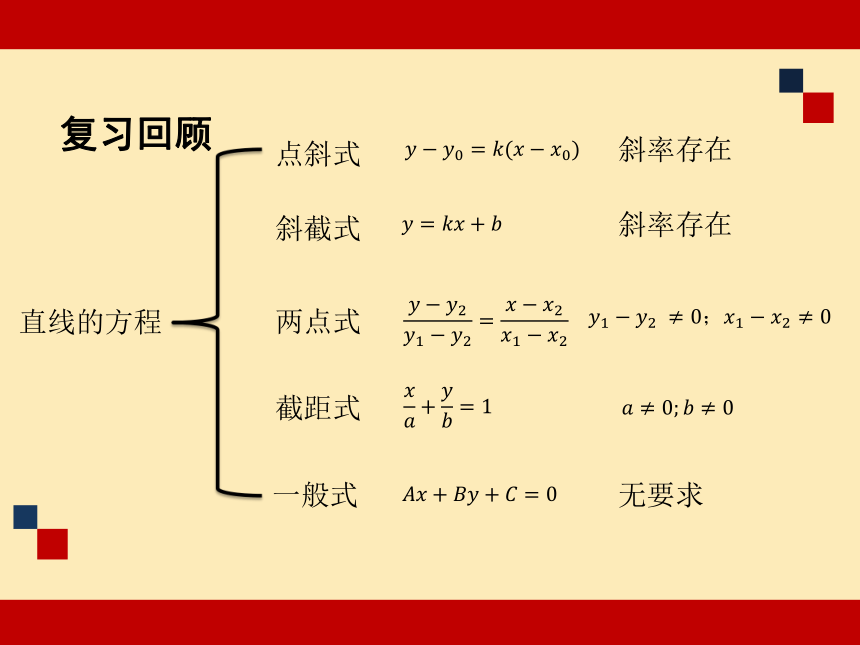
复习回顾
直线的方程
点斜式
斜截式
一般式
两点式
截距式
?????????0=????(?????????0)
?
????=????????+????
?
?????????2????1?????2=?????????2????1?????2
?
????????+????????=1
?
????????+????????+????=0
?
斜率存在
斜率存在
????1?????2?≠0;????1?????2≠0
?
????≠0;????≠0
?
无要求
学习目标
1.从直线的交点和法向量两个方面掌握直线位置关系和方程各项系数的等价关系。
2.会根据直线方程的系数判断两条直线相交、平行、重合。
复习回顾
在 平面内 的两条直线称为平行直线
同一个
不相交
关键词:
不相交
代表了没有交点
????
?
????
?
直线平行的定义:
思考:1、如何使用定义来证明直线平行?
2、如何使用方程的语言描述两条直线没有交点?
????
?
????
?
????
?
????
?
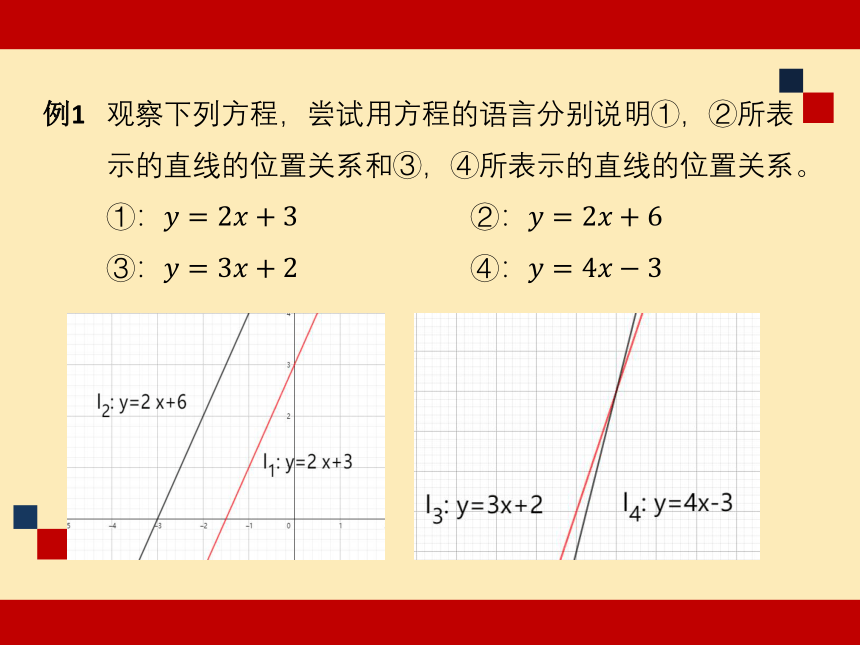
例1
观察下列方程,尝试用方程的语言分别说明①,②所表
示的直线的位置关系和③,④所表示的直线的位置关系。
①:????=2????+3 ②:????=2????+6
③:????=3????+2 ④:????=4?????3
?
?
归纳总结
对于????1:??????=????1????+????1与????2:??????=????2????+????2,联立两个直线方程得
?
&????=????1????+????1&????=????2????+????2
?
得
????1?????2????=(????2?????1)
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}?
系数的情况
方程解的情况
代表的直线位置情况
情况一
????1=????2?, ????1=????2
无数解?
重合?
情况二
?????1=????2?, ????1≠????2?
无解?
?平行
情况三
?????1≠????2?
唯一解?
相交?
例2
如果直线????1:??????=????????+3与直线????2:??????=4????+4平行
求????的值。
?
新问题的产生
斜截式方程并不能表示全部直线
是否有一种直线方程可以表示全部直线?
从向量的角度去解决问题
对于直线????2:??????1????+????1????+????1=0与直线????2:??????2????+????2????+????2=0,他们的法向量分别是
?
????1=(????1,????1)和????2=(????2,????2)
?
&????1/????2<==>????1与????2平行或重合?&&????1/????2<==>????1与????2相交
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}l1与l2相交
l1与l2平行
???
l1与l2重合
??
????1????2≠????2????1??
?
????1=????????2????1=????????2????1≠????????2
?
????1=????????2????1=????????2????1=????????2?
?
例3
判断以下两对直线的位置关系,如果相交,求出交点坐标:
????1:???????????+1=0,???????????2:??2?????2????+1=0
????3:???????2????+1=0,????????4:??????+2????+5=0
?
?
例4
已知直线????过点(1,?4)且与直线2????+3????+5=0平行,求直线????的方程。
?
回顾总结
在本节课你收获了什么知识?
谢谢聆听
时间:2020年11月4日
主讲人:
复习回顾
直线的方程
点斜式
斜截式
一般式
两点式
截距式
?????????0=????(?????????0)
?
????=????????+????
?
?????????2????1?????2=?????????2????1?????2
?
????????+????????=1
?
????????+????????+????=0
?
斜率存在
斜率存在
????1?????2?≠0;????1?????2≠0
?
????≠0;????≠0
?
无要求
学习目标
1.从直线的交点和法向量两个方面掌握直线位置关系和方程各项系数的等价关系。
2.会根据直线方程的系数判断两条直线相交、平行、重合。
复习回顾
在 平面内 的两条直线称为平行直线
同一个
不相交
关键词:
不相交
代表了没有交点
????
?
????
?
直线平行的定义:
思考:1、如何使用定义来证明直线平行?
2、如何使用方程的语言描述两条直线没有交点?
????
?
????
?
????
?
????
?
例1
观察下列方程,尝试用方程的语言分别说明①,②所表
示的直线的位置关系和③,④所表示的直线的位置关系。
①:????=2????+3 ②:????=2????+6
③:????=3????+2 ④:????=4?????3
?
?
归纳总结
对于????1:??????=????1????+????1与????2:??????=????2????+????2,联立两个直线方程得
?
&????=????1????+????1&????=????2????+????2
?
得
????1?????2????=(????2?????1)
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}?
系数的情况
方程解的情况
代表的直线位置情况
情况一
????1=????2?, ????1=????2
无数解?
重合?
情况二
?????1=????2?, ????1≠????2?
无解?
?平行
情况三
?????1≠????2?
唯一解?
相交?
例2
如果直线????1:??????=????????+3与直线????2:??????=4????+4平行
求????的值。
?
新问题的产生
斜截式方程并不能表示全部直线
是否有一种直线方程可以表示全部直线?
从向量的角度去解决问题
对于直线????2:??????1????+????1????+????1=0与直线????2:??????2????+????2????+????2=0,他们的法向量分别是
?
????1=(????1,????1)和????2=(????2,????2)
?
&????1/????2<==>????1与????2平行或重合?&&????1/????2<==>????1与????2相交
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}l1与l2相交
l1与l2平行
???
l1与l2重合
??
????1????2≠????2????1??
?
????1=????????2????1=????????2????1≠????????2
?
????1=????????2????1=????????2????1=????????2?
?
例3
判断以下两对直线的位置关系,如果相交,求出交点坐标:
????1:???????????+1=0,???????????2:??2?????2????+1=0
????3:???????2????+1=0,????????4:??????+2????+5=0
?
?
例4
已知直线????过点(1,?4)且与直线2????+3????+5=0平行,求直线????的方程。
?
回顾总结
在本节课你收获了什么知识?
谢谢聆听
