高中数学人教A版必修一:2.1.2 指数函数及其性质 课件(17张PPT)
文档属性
| 名称 | 高中数学人教A版必修一:2.1.2 指数函数及其性质 课件(17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 458.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-20 16:47:20 | ||
图片预览




文档简介
数学是打开科学大门的钥匙, 轻视数学必将造成对一切知识的损害,因为轻视数学的人不可能掌握其它学科和理解万物。
————弗·培根
指数函数及其性质(1)
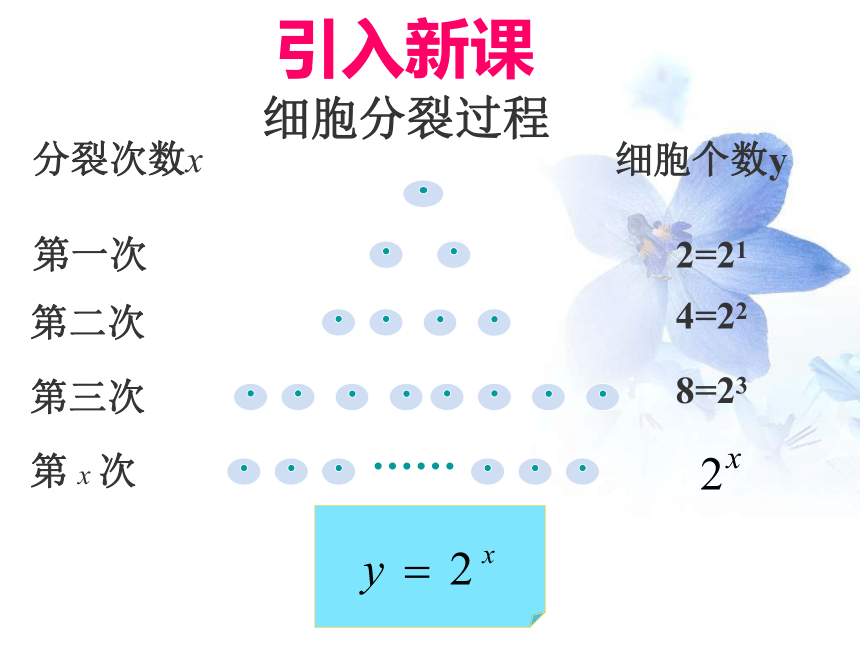
细胞分裂过程
细胞个数y
2=21
8=23
4=22
…………
分裂次数x
第二次
第三次
第 x 次
第一次
……
引入新课
…...
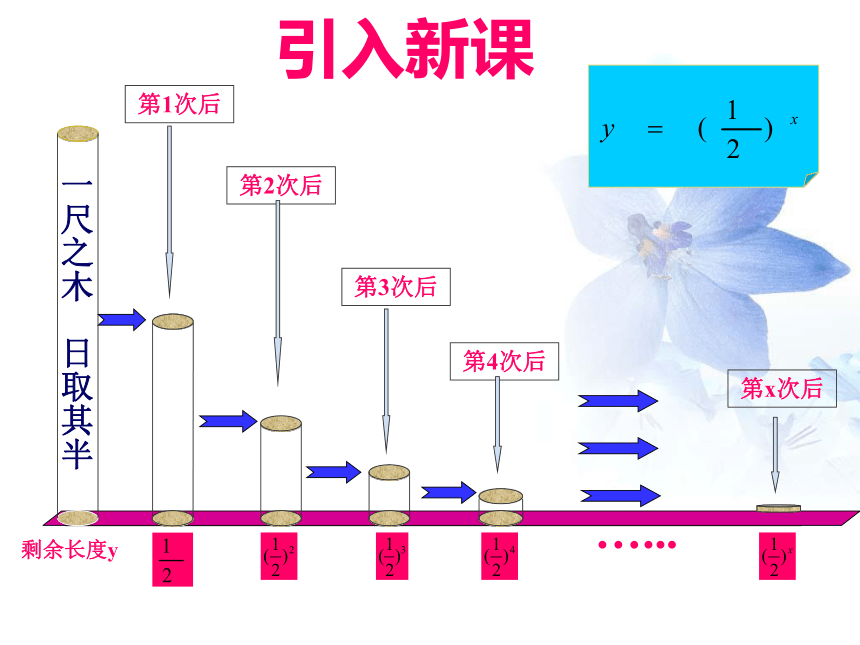
剩余长度y
一尺之木 日取其半
第1次后
第2次后
第3次后
第4次后
第x次后
引入新课
仔细观察这两个函数表达式的底数和指数,请问你有什么发现?
思考1
一般地,形如
的函数叫做指数函数,
函数的定义域是 R .
其中
是自变量.
讲授新课
?
?
0
1
a
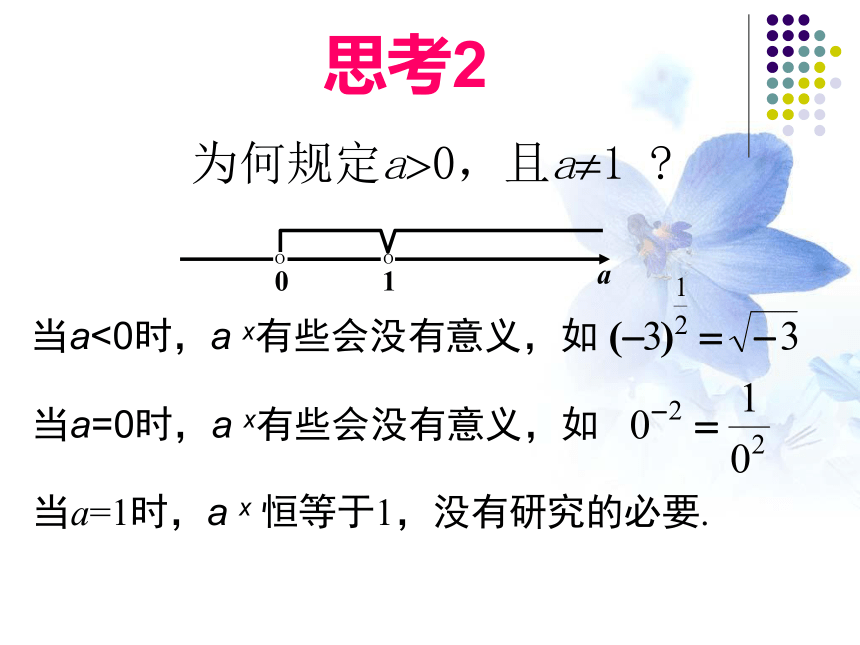
当a=1时,a x 恒等于1,没有研究的必要.
为何规定a?0,且a?1 ?
当a<0时,a x有些会没有意义,如
当a=0时,a x有些会没有意义,如
思考2
下列函数中,那些是指数函数? .
(1) (7)
(1) (2)
(3) (4)
(5) (6)
(7)
课堂练习
常数(大于0且不等于1)
自变量
系数为1
y=1 · ax
知识小结
完成讲学稿中变式练习
课堂练习
作出函数 与 的图象
讲授新课
y
x
0
· (0,1)
指数函数 的图象和性质
1. 定义域:
2. 值 域:
3. 过 点:
4. 单调性:
5. 函数值的变化情况:
当 x < 0时, 0< y <1.
R ;
( 0 , +∞) ;
( 0 , 1) ;
在 R 上是增函数;
当 x > 0时, y > 1.
讲授新课
在R上是减函数
在R上是增函数
单调性
(0,1)
(0,1)
过定点
R
R
值 域
(0,+∞)
(0,+∞)
定义域
图 象
函 数
R
(0,+∞)
(0,1)
知识小结
例1. 比较下列各题中两个值的大小:
(1)1.72.5 , 1.73 ; (2)0.8-0.1 ,0.8 -0.2
(3) 22.5 , 0.5-3 ; (4)1.70.3 , 0.93.1.
小结 比较指数幂大小的方法:
①单调性法:利用函数的单调性,
数的特征是底同指不同(包括可以化为同底的)。
②中间值法:找一个 “中间值”如“1”来过渡,
数的特征是底不同。
应用举例
(1)已知0.3x≥0.37,求实数x的取值范围.
(2)已知 5x< , 求实数x的取值范围.
变式练习
3.会比较指数的大小。
2.研究函数的一般步骤:定义→图象→性质→应用;
1.数学知识点: 指数函数的概念、图象和性质;
课堂小结
作业布置
必做题:讲学稿中达标检测
选做题:课本60页B组1,2
谢谢!
————弗·培根
指数函数及其性质(1)
细胞分裂过程
细胞个数y
2=21
8=23
4=22
…………
分裂次数x
第二次
第三次
第 x 次
第一次
……
引入新课
…...
剩余长度y
一尺之木 日取其半
第1次后
第2次后
第3次后
第4次后
第x次后
引入新课
仔细观察这两个函数表达式的底数和指数,请问你有什么发现?
思考1
一般地,形如
的函数叫做指数函数,
函数的定义域是 R .
其中
是自变量.
讲授新课
?
?
0
1
a
当a=1时,a x 恒等于1,没有研究的必要.
为何规定a?0,且a?1 ?
当a<0时,a x有些会没有意义,如
当a=0时,a x有些会没有意义,如
思考2
下列函数中,那些是指数函数? .
(1) (7)
(1) (2)
(3) (4)
(5) (6)
(7)
课堂练习
常数(大于0且不等于1)
自变量
系数为1
y=1 · ax
知识小结
完成讲学稿中变式练习
课堂练习
作出函数 与 的图象
讲授新课
y
x
0
· (0,1)
指数函数 的图象和性质
1. 定义域:
2. 值 域:
3. 过 点:
4. 单调性:
5. 函数值的变化情况:
当 x < 0时, 0< y <1.
R ;
( 0 , +∞) ;
( 0 , 1) ;
在 R 上是增函数;
当 x > 0时, y > 1.
讲授新课
在R上是减函数
在R上是增函数
单调性
(0,1)
(0,1)
过定点
R
R
值 域
(0,+∞)
(0,+∞)
定义域
图 象
函 数
R
(0,+∞)
(0,1)
知识小结
例1. 比较下列各题中两个值的大小:
(1)1.72.5 , 1.73 ; (2)0.8-0.1 ,0.8 -0.2
(3) 22.5 , 0.5-3 ; (4)1.70.3 , 0.93.1.
小结 比较指数幂大小的方法:
①单调性法:利用函数的单调性,
数的特征是底同指不同(包括可以化为同底的)。
②中间值法:找一个 “中间值”如“1”来过渡,
数的特征是底不同。
应用举例
(1)已知0.3x≥0.37,求实数x的取值范围.
(2)已知 5x< , 求实数x的取值范围.
变式练习
3.会比较指数的大小。
2.研究函数的一般步骤:定义→图象→性质→应用;
1.数学知识点: 指数函数的概念、图象和性质;
课堂小结
作业布置
必做题:讲学稿中达标检测
选做题:课本60页B组1,2
谢谢!
