人教A版高中数学必修一第二章:2.2.1对数运算性质第2,3课时 课件(28张PPT)
文档属性
| 名称 | 人教A版高中数学必修一第二章:2.2.1对数运算性质第2,3课时 课件(28张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 576.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-20 00:00:00 | ||
图片预览








文档简介
2.2.1 对数与对数运算(2)
一般地,如果
的b次幂等于N, 即
那么数 b就叫做
以a为底 N的对数,记作
a叫做对数的底数,N叫做真数。
定义:
知识回放
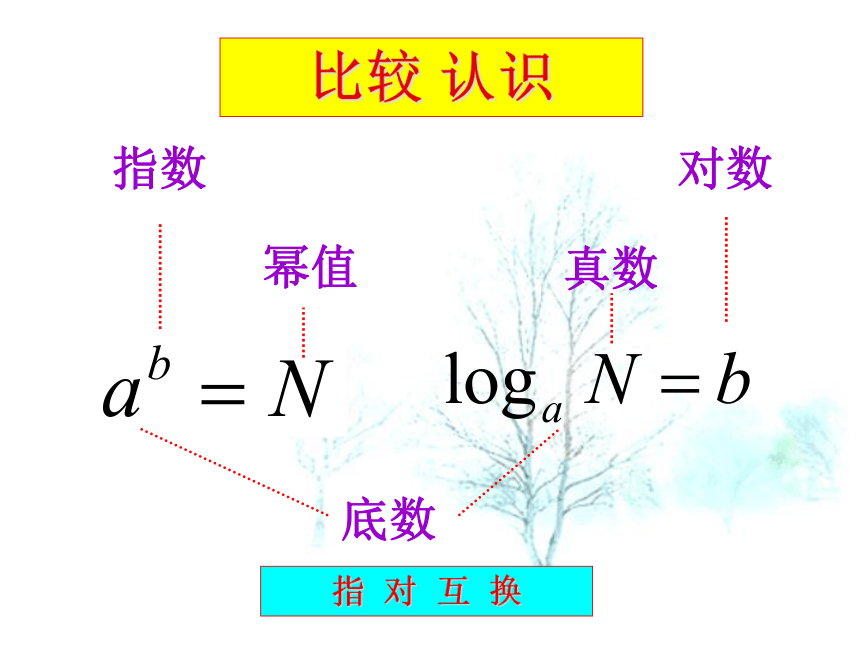
底数
幂值
真数
指数
对数
比较 认识
指 对 互 换
四个恒等式:
二、学习新内容:
积、商、幂的对数运算法则:
如果 a > 0,a ? 1,M > 0, N > 0 有:
对这三个性质的理解:它其实是对幂的运算性质的另一种表达。(幂运算的逆运算)
上述关于对数运算的三个运算法则如何用文字语言描述?
两数积的对数,等于各数的对数的和;
两数商的对数,等于被除数的对数减去除数的对数;
幂的对数等于幂指数乘以底数的对数.
证明: 设
由对数的定义可以得:
∴MN=
即证得
几点说明
1、公式中为什么加上条件M>0,N>0?
2、公式能够从右到左运用吗?
3、由性质1可得
由性质3可得常用的两个结论
这是为了保证所得结果中的对数都存在例如:lg[(-2)(-1)]=lg2存在,但lg(-2),lg(-1)都不存在。
辨析1:
关于对数的运算性质,下列说法正确的有( ).
D
辨析2:
下列7个式子中,其中正确的有:
(3) (6) (7)
例1
解(1)
解(2)
用
表示下列各式:
2、用lgx,lgy,lgz表示下列各式:
(2)
(1)
=lgx+3lgy-
lgz;
例2 计算下列各式的值:
(1)
解 :
=5+14=19
解 :
(2)
1、计算:
解:
练习:
课堂练习:
课本68页第1、2、3题
如果 a > 0,a ? 1,M > 0, N > 0 有:
课堂小结:
作业布置:
课本74页A组第3、4、5题
⑴ 若
⑵ 的值为______
⑶
拓展练习:
2
2.2.1 对数与对数运算(3)
如果 a > 0,a ? 1,M > 0, N > 0 有:
知识回放
⑴ 若
⑵ 的值为______
⑶
练习:
2
思考:
证明:
这就是对数里很重要的一个公式:换底公式
log
b
x
b
a
a
x
=
?
=
证明下式:
利用关系式
利用换底公式证明下列式子:
证明:
例1.求 的值
解:
=3
例2:
例6 生物机体内碳14的半衰期为5730年,湖南长沙马王堆汉墓女尸出土时碳14的残余量约占原始含量的76.7%,试推算马王堆汉墓的年代。
课堂练习:
课本第68页第4题
作业布置:
第 75 页 A组 第11题
第82页 A组 第3题
小结:
换底公式:
2、已知
试用a, b 表示
拓展练习:
1、计算下列各式的值:
(1)
一般地,如果
的b次幂等于N, 即
那么数 b就叫做
以a为底 N的对数,记作
a叫做对数的底数,N叫做真数。
定义:
知识回放
底数
幂值
真数
指数
对数
比较 认识
指 对 互 换
四个恒等式:
二、学习新内容:
积、商、幂的对数运算法则:
如果 a > 0,a ? 1,M > 0, N > 0 有:
对这三个性质的理解:它其实是对幂的运算性质的另一种表达。(幂运算的逆运算)
上述关于对数运算的三个运算法则如何用文字语言描述?
两数积的对数,等于各数的对数的和;
两数商的对数,等于被除数的对数减去除数的对数;
幂的对数等于幂指数乘以底数的对数.
证明: 设
由对数的定义可以得:
∴MN=
即证得
几点说明
1、公式中为什么加上条件M>0,N>0?
2、公式能够从右到左运用吗?
3、由性质1可得
由性质3可得常用的两个结论
这是为了保证所得结果中的对数都存在例如:lg[(-2)(-1)]=lg2存在,但lg(-2),lg(-1)都不存在。
辨析1:
关于对数的运算性质,下列说法正确的有( ).
D
辨析2:
下列7个式子中,其中正确的有:
(3) (6) (7)
例1
解(1)
解(2)
用
表示下列各式:
2、用lgx,lgy,lgz表示下列各式:
(2)
(1)
=lgx+3lgy-
lgz;
例2 计算下列各式的值:
(1)
解 :
=5+14=19
解 :
(2)
1、计算:
解:
练习:
课堂练习:
课本68页第1、2、3题
如果 a > 0,a ? 1,M > 0, N > 0 有:
课堂小结:
作业布置:
课本74页A组第3、4、5题
⑴ 若
⑵ 的值为______
⑶
拓展练习:
2
2.2.1 对数与对数运算(3)
如果 a > 0,a ? 1,M > 0, N > 0 有:
知识回放
⑴ 若
⑵ 的值为______
⑶
练习:
2
思考:
证明:
这就是对数里很重要的一个公式:换底公式
log
b
x
b
a
a
x
=
?
=
证明下式:
利用关系式
利用换底公式证明下列式子:
证明:
例1.求 的值
解:
=3
例2:
例6 生物机体内碳14的半衰期为5730年,湖南长沙马王堆汉墓女尸出土时碳14的残余量约占原始含量的76.7%,试推算马王堆汉墓的年代。
课堂练习:
课本第68页第4题
作业布置:
第 75 页 A组 第11题
第82页 A组 第3题
小结:
换底公式:
2、已知
试用a, b 表示
拓展练习:
1、计算下列各式的值:
(1)
