人教A版高中数学必修一第一章:1.1.3 集合的基本运算(1) 课件(16张PPT)
文档属性
| 名称 | 人教A版高中数学必修一第一章:1.1.3 集合的基本运算(1) 课件(16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 118.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-20 16:49:01 | ||
图片预览






文档简介
1.1.3 集合的基本运算(1)
作业问题:
1、布置的习题作业或者补充作业一定要抄上题目。
以后不抄题目的扣分。
2、解答过程中一定要先写上“解:”,考试时不写上“解”的一定会扣分的;要设字母的一定说明清楚所表达的意思。
比如:P12 3(1) 解:设A为大于1且小于6的整数所构成的集合,则A={2,3,4,5}。
作业问题:
3、课本上出现的例题或者辅导书上的例题,同学们一定要记清楚它的书写格式和解题步骤,考试时书写格式要规范,解题
的每一步骤都要写详细(它怎么的来的?)。考试时是按解题的步骤给分的,每一步骤对应相应的分数,少或错了一步,都是不给分的。
4、无论是作业或者考试,书写一定要工整,简洁,明了,这能给老师一个良好的印象分。
作 业讲评1
1、课本P12:
2、
第3、4题
3、已知A={a-2,2a2+5a,10},且
-3∈A,求a。
作业讲评2
1、P12 A组 第5 题(填在书上)
2、P44 A组 第4题
3、设A={x , x2 , xy} , B={1 , x , y} ,
且A=B,求实数x , y的值.
观察集合A,B,C元素间的关系:
(1) A={4,5,6,8},B={3,5,7,8},
C={3,4,5,6,7,8}
(2) A={x|x是有理数},B={x|x是无理数},
C={x|x是实数}
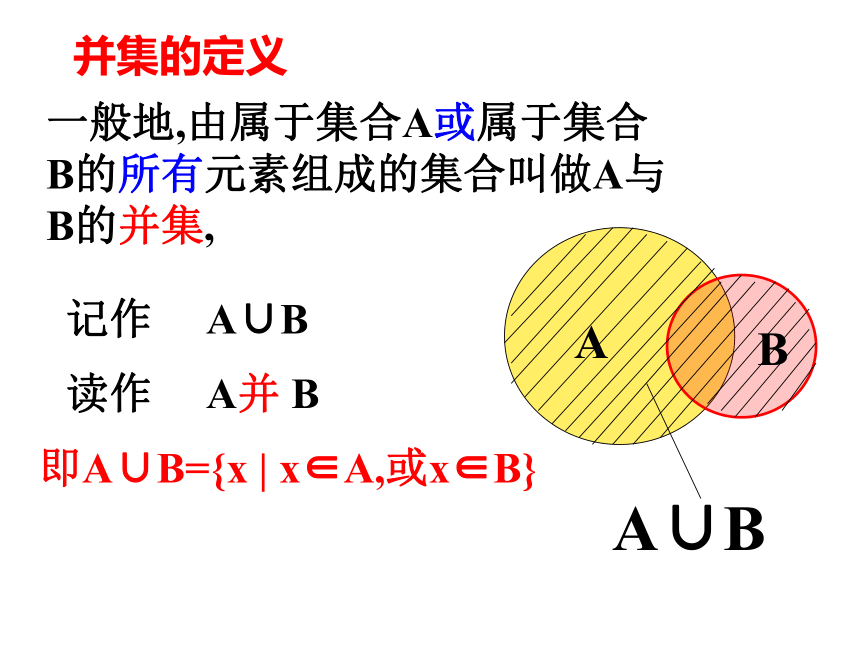
并集的定义
一般地,由属于集合A或属于集合B的所有元素组成的集合叫做A与B的并集,
记作 A∪B
即A∪B={x | x∈A,或x∈B}
读作 A并 B
A
B
A∪B
并集的性质:
1、A∪A = A∪φ =
A
A
=
2、A∪B B∪A
3、A A∪B
B A∪B
4、若A∪B=A,则B A .反之亦然。
例1. A={4,5,6,8},B={3,5,7,8},求A∪B.
例2.设A={x|-1 A={4,5,6,8},
B={3,5,7,8},
C={5,8}
观察集合A,B,C元素间的关系:
交集的定义
一般地,由既属于集合A又属于集合B的所有元素组成的集合叫做A与B的交集.
记作 A∩B
即 A∩B={x |x∈A,且x∈B}
读作 A交 B
A
B
A∩B
性 质1
A∩A = A∩φ =
A
φ
=
A∩B B∩A
性 质2
性 质3
A∩B A
A∩B B
若A∩B=A,则A B.
反之亦然.
例3.新华中学开运动会,设
A={x|x是新华中学高一年级参加百米赛跑的同学}
B={x|x是新华中学高一年级参加跳高比赛的同学}
求:A∩B
例4.设平面内直线l1上点的集合为L1,直线l2上点的集合为L2试用集合的运算表示l1,l2的位置关系。
课堂练习
教材P11练习1~3
课堂小结
1. 理解两个集合交集与并集的概念bb和性质.
2. 求两个集合的交集与并集,常用 bb 数轴法和图示法(Venn图).
3.解题时要灵活、准确地运用交集、并集的性质,涉及到字母时,要对字母进行讨论,并检验符不符合题意。
1、教材P12 A组第 6,7 题
作业布置
2、设集合A={ -4,2m-1, m2 },
B={9,m-5,1-m},又A∩B={9},
求实数m的值.
作业问题:
1、布置的习题作业或者补充作业一定要抄上题目。
以后不抄题目的扣分。
2、解答过程中一定要先写上“解:”,考试时不写上“解”的一定会扣分的;要设字母的一定说明清楚所表达的意思。
比如:P12 3(1) 解:设A为大于1且小于6的整数所构成的集合,则A={2,3,4,5}。
作业问题:
3、课本上出现的例题或者辅导书上的例题,同学们一定要记清楚它的书写格式和解题步骤,考试时书写格式要规范,解题
的每一步骤都要写详细(它怎么的来的?)。考试时是按解题的步骤给分的,每一步骤对应相应的分数,少或错了一步,都是不给分的。
4、无论是作业或者考试,书写一定要工整,简洁,明了,这能给老师一个良好的印象分。
作 业讲评1
1、课本P12:
2、
第3、4题
3、已知A={a-2,2a2+5a,10},且
-3∈A,求a。
作业讲评2
1、P12 A组 第5 题(填在书上)
2、P44 A组 第4题
3、设A={x , x2 , xy} , B={1 , x , y} ,
且A=B,求实数x , y的值.
观察集合A,B,C元素间的关系:
(1) A={4,5,6,8},B={3,5,7,8},
C={3,4,5,6,7,8}
(2) A={x|x是有理数},B={x|x是无理数},
C={x|x是实数}
并集的定义
一般地,由属于集合A或属于集合B的所有元素组成的集合叫做A与B的并集,
记作 A∪B
即A∪B={x | x∈A,或x∈B}
读作 A并 B
A
B
A∪B
并集的性质:
1、A∪A = A∪φ =
A
A
=
2、A∪B B∪A
3、A A∪B
B A∪B
4、若A∪B=A,则B A .反之亦然。
例1. A={4,5,6,8},B={3,5,7,8},求A∪B.
例2.设A={x|-1
B={3,5,7,8},
C={5,8}
观察集合A,B,C元素间的关系:
交集的定义
一般地,由既属于集合A又属于集合B的所有元素组成的集合叫做A与B的交集.
记作 A∩B
即 A∩B={x |x∈A,且x∈B}
读作 A交 B
A
B
A∩B
性 质1
A∩A = A∩φ =
A
φ
=
A∩B B∩A
性 质2
性 质3
A∩B A
A∩B B
若A∩B=A,则A B.
反之亦然.
例3.新华中学开运动会,设
A={x|x是新华中学高一年级参加百米赛跑的同学}
B={x|x是新华中学高一年级参加跳高比赛的同学}
求:A∩B
例4.设平面内直线l1上点的集合为L1,直线l2上点的集合为L2试用集合的运算表示l1,l2的位置关系。
课堂练习
教材P11练习1~3
课堂小结
1. 理解两个集合交集与并集的概念bb和性质.
2. 求两个集合的交集与并集,常用 bb 数轴法和图示法(Venn图).
3.解题时要灵活、准确地运用交集、并集的性质,涉及到字母时,要对字母进行讨论,并检验符不符合题意。
1、教材P12 A组第 6,7 题
作业布置
2、设集合A={ -4,2m-1, m2 },
B={9,m-5,1-m},又A∩B={9},
求实数m的值.
