人教A版数学必修1第三章3.1.2 用二分法求方程的近似解课件(共18张PPT)
文档属性
| 名称 | 人教A版数学必修1第三章3.1.2 用二分法求方程的近似解课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 246.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-19 00:00:00 | ||
图片预览






文档简介
数值逼近的其中一个思想:
将数轴上的一个区间无限缩小,最终将逼近到数轴上的一个点。
思考:求下列方程的解
(1)
(2)
(3)
2x-16=0
x2-3x-4=0
lnx+2x-6=0
?
解得:x=8
解得:x=-1或4
逼近零点
寻找函数f(x)=lnx+2x-6的零点。
f(2)f(3)<0,
零点在(2,3)里,且只有一个零点。
接下来,就该去(2,3)里找这个零点啦!
f(x)的定义域为(0,+∞),单调递增。
用二分法求方程的近似解
二分法的定义
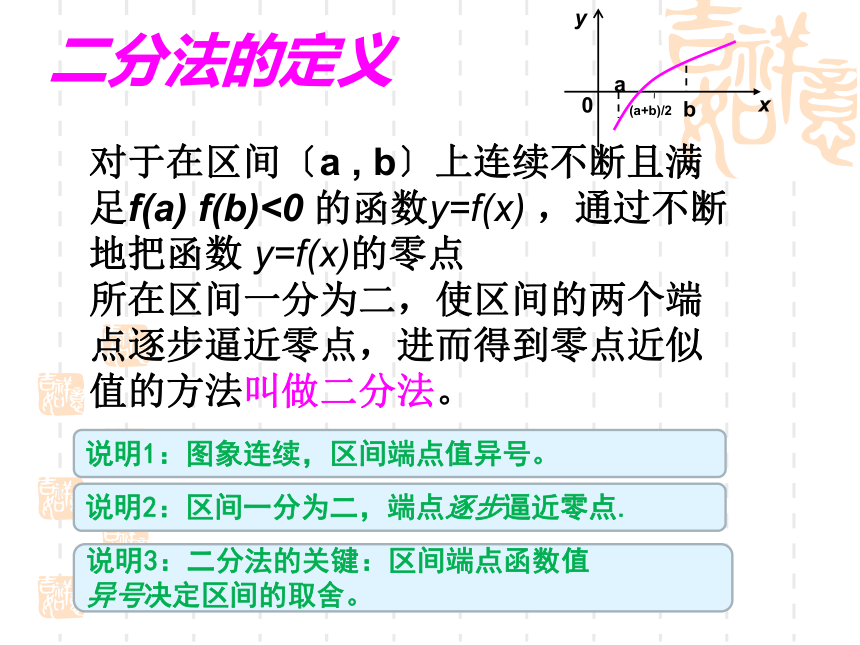
对于在区间〔a , b〕上连续不断且满足f(a) f(b)<0 的函数y=f(x) ,通过不断地把函数 y=f(x)的零点
所在区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法。
x
y
0
a
b
(a+b)/2
说明1:图象连续,区间端点值异号。
说明2:区间一分为二,端点逐步逼近零点.
说明3:二分法的关键:区间端点函数值 异号决定区间的取舍。
用二分法找出函数f(x)=lnx+2x-6 在区间(2, 3)内的零点近似值?
(精确到0.01)
次数
(a+b)/2
f[(a+b)/2]
区间(a,b)
|a-b|
1
2
3
4
5
6
7
f(x)=lnx+2x-6
f(2)=-1.3069
f(3)=1.0986
2.5
-0.084
2.75
0.512
2.625
0.215
2.5625
0.066
0.5
0.25
0.125
0.0625
(2.5,3)
(2.5 , 2.75)
(2.5 , 2.625)
(2.5 , 2.5625)
2.53125
-0.009
2.546875
0.029
2.5390625
0.010
0.03125
0.015625
0.0078125
(2.53125 , 2.5625)
(2.53125 , 2.546875)
(2.53125 , 2.5390625)
因为精确度ε为0.01,
且∣2.53125 —2.5390625∣=0.0078125<0.01
所以,方程lnx+2x-6=0的近似解是x=2.5390625。
能否根据二分法求方程近似解的过程归纳其一般步骤?
1,确定区间〔a,b〕,验证f(a) f(b)<0 ,
给定精确度ε;
3,计算 f(c)的值
2,求区间 (a,b) 的中点c;
(1)若 f(c) =0 ,则c就是函数的零点;
(2)若 f(a) f(c)<0 ,则令b=c(此时零点
x0∈(a,c));
(3)若 f(c) f(b)<0 ,则令a=c(此时零点
x0∈(c,b))。
步骤:
4,判断是否达到精确度ε:即若| |<ε,
则得到零点近似值 (或 );否则重复2~4。
选初始区间
取区间中点
中点函
数值为零
结束
是
定新区间
否
区间长度
小于精确度
否
是
x
y
x
y
x
y
x
y
练习1
下列函数图象与x轴均有交点,其中不能用二
分法求图中交点横坐标的是( )
A
D
C
B
B
练习2
A
D
C
B
函数 在区间[-2,4]上的零点必定属于区间( )。
C
[-2,1]
[-2,-1/2]
[7/4,5/2]
[1,7/4]
用二分法求方程2x+3x-7=0的近似解
(精确度0.1)
操 作
近似解为1.4375
小 结
1.数值逼近的思想
2.二分法的定义
3.用二分法求方程近似解的步骤
函数
方程
转
化
思
想
逼
近
思
想
数学
源于生活
数学
用于生活
小结
二分法
数形结合
1.寻找解所在的区间
2.不断二分解所在的区间
3.根据精确度得出近似解
用二分法求
方程的近似解
算法思想
作 业
1、回忆本堂内容(二分法你会用了吗?)
2、
将数轴上的一个区间无限缩小,最终将逼近到数轴上的一个点。
思考:求下列方程的解
(1)
(2)
(3)
2x-16=0
x2-3x-4=0
lnx+2x-6=0
?
解得:x=8
解得:x=-1或4
逼近零点
寻找函数f(x)=lnx+2x-6的零点。
f(2)f(3)<0,
零点在(2,3)里,且只有一个零点。
接下来,就该去(2,3)里找这个零点啦!
f(x)的定义域为(0,+∞),单调递增。
用二分法求方程的近似解
二分法的定义
对于在区间〔a , b〕上连续不断且满足f(a) f(b)<0 的函数y=f(x) ,通过不断地把函数 y=f(x)的零点
所在区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法。
x
y
0
a
b
(a+b)/2
说明1:图象连续,区间端点值异号。
说明2:区间一分为二,端点逐步逼近零点.
说明3:二分法的关键:区间端点函数值 异号决定区间的取舍。
用二分法找出函数f(x)=lnx+2x-6 在区间(2, 3)内的零点近似值?
(精确到0.01)
次数
(a+b)/2
f[(a+b)/2]
区间(a,b)
|a-b|
1
2
3
4
5
6
7
f(x)=lnx+2x-6
f(2)=-1.3069
f(3)=1.0986
2.5
-0.084
2.75
0.512
2.625
0.215
2.5625
0.066
0.5
0.25
0.125
0.0625
(2.5,3)
(2.5 , 2.75)
(2.5 , 2.625)
(2.5 , 2.5625)
2.53125
-0.009
2.546875
0.029
2.5390625
0.010
0.03125
0.015625
0.0078125
(2.53125 , 2.5625)
(2.53125 , 2.546875)
(2.53125 , 2.5390625)
因为精确度ε为0.01,
且∣2.53125 —2.5390625∣=0.0078125<0.01
所以,方程lnx+2x-6=0的近似解是x=2.5390625。
能否根据二分法求方程近似解的过程归纳其一般步骤?
1,确定区间〔a,b〕,验证f(a) f(b)<0 ,
给定精确度ε;
3,计算 f(c)的值
2,求区间 (a,b) 的中点c;
(1)若 f(c) =0 ,则c就是函数的零点;
(2)若 f(a) f(c)<0 ,则令b=c(此时零点
x0∈(a,c));
(3)若 f(c) f(b)<0 ,则令a=c(此时零点
x0∈(c,b))。
步骤:
4,判断是否达到精确度ε:即若| |<ε,
则得到零点近似值 (或 );否则重复2~4。
选初始区间
取区间中点
中点函
数值为零
结束
是
定新区间
否
区间长度
小于精确度
否
是
x
y
x
y
x
y
x
y
练习1
下列函数图象与x轴均有交点,其中不能用二
分法求图中交点横坐标的是( )
A
D
C
B
B
练习2
A
D
C
B
函数 在区间[-2,4]上的零点必定属于区间( )。
C
[-2,1]
[-2,-1/2]
[7/4,5/2]
[1,7/4]
用二分法求方程2x+3x-7=0的近似解
(精确度0.1)
操 作
近似解为1.4375
小 结
1.数值逼近的思想
2.二分法的定义
3.用二分法求方程近似解的步骤
函数
方程
转
化
思
想
逼
近
思
想
数学
源于生活
数学
用于生活
小结
二分法
数形结合
1.寻找解所在的区间
2.不断二分解所在的区间
3.根据精确度得出近似解
用二分法求
方程的近似解
算法思想
作 业
1、回忆本堂内容(二分法你会用了吗?)
2、
