人教A版高中数学必修一第二章阶段检测(word版含解析)
文档属性
| 名称 | 人教A版高中数学必修一第二章阶段检测(word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 325.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-19 00:00:00 | ||
图片预览



文档简介
阶段检测(二)
测试范围:一元二次函数、方程和不等式
选择题部分(共40分)
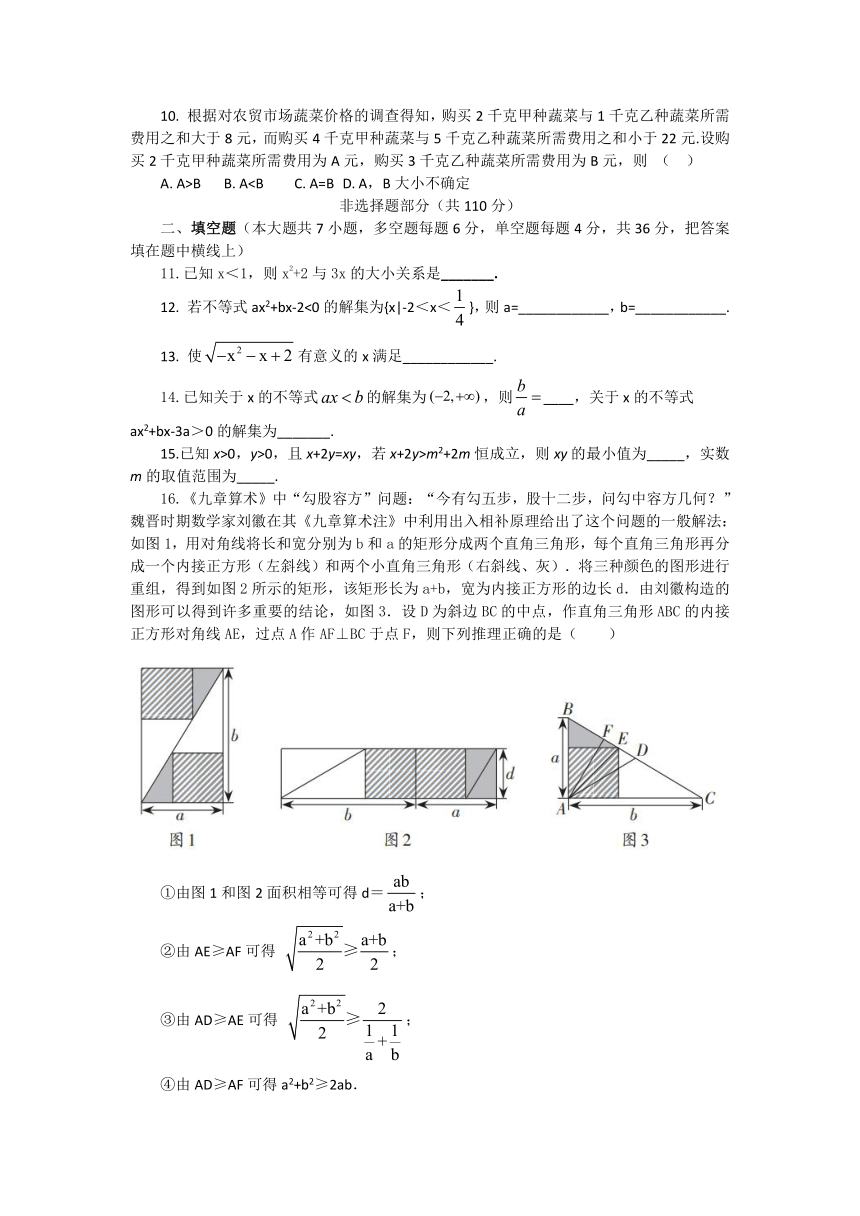
一、选择题(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1. 若falseA.false>false B. a|b| D. a2>b2
2.给出下列不等式:
①a2+3>2a;
②a2+b2>2(a-b-1);
③x2+y2>2xy;
④a+b≥2false.
其中恒成立的不等式的个数为 ( )
A. 3 B. 2 C. 1 D. 0
3. 已知集合A={x|x>1},B={x|x2-2x<0},则A∪B= ( )
A. {x|x>0}B. {x|x>1}C. {x|14.false(x>0)取最大值时x的值为 ( )
A. 2 B.false C.false D. false
5. 已知矩形的相邻边长x,y满足4x+3y=12,则该矩形面积的最大值为 ( )
A. 3 B. 6 C. 8 D. 9
6. 若正数a,b满足ab-a-b=1,则a+b的最小值为 ( )
A. 2+2false B.2-2false C. -false D.-2false
7. 若关于x的不等式x2-ax-6a2>0(a<0)的解集为{x|x<x1,或x>x2},且x2-x1=5false,则a= ( )
A.- false B. -false C. -false D. -false
8. 若0false,则a,b的大小关系是( )
A. ab D. a≥b
9. 已知不等式(x+y)(false)≥9对任意正实数x,y恒成立,则正实数a的最小值是 ( )
A. 2 B. 4 C. 6 D. 8
10. 根据对农贸市场蔬菜价格的调查得知,购买2千克甲种蔬菜与1千克乙种蔬菜所需费用之和大于8元,而购买4千克甲种蔬菜与5千克乙种蔬菜所需费用之和小于22元.设购买2千克甲种蔬菜所需费用为A元,购买3千克乙种蔬菜所需费用为B元,则 ( )
A. A>B B. A非选择题部分(共110分)
二、填空题(本大题共7小题,多空题每题6分,单空题每题4分,共36分,把答案填在题中横线上)
11.已知x<1,则x2+2与3x的大小关系是_______.
12. 若不等式ax2+bx-2<0的解集为{x|-2<x<false},则a=____________,b=____________.
13. 使false有意义的x满足____________.
14.已知关于x的不等式false的解集为false,则false____,关于x的不等式ax2+bx-3a>0的解集为_______.
15.已知x>0,y>0,且x+2y=xy,若x+2y>m2+2m恒成立,则xy的最小值为_____,实数m的取值范围为_____.
16.《九章算术》中“勾股容方”问题:“今有勾五步,股十二步,问勾中容方几何?”魏晋时期数学家刘徽在其《九章算术注》中利用出入相补原理给出了这个问题的一般解法:如图1,用对角线将长和宽分别为b和a的矩形分成两个直角三角形,每个直角三角形再分成一个内接正方形(左斜线)和两个小直角三角形(右斜线、灰).将三种颜色的图形进行重组,得到如图2所示的矩形,该矩形长为a+b,宽为内接正方形的边长d.由刘徽构造的图形可以得到许多重要的结论,如图3.设D为斜边BC的中点,作直角三角形ABC的内接正方形对角线AE,过点A作AF⊥BC于点F,则下列推理正确的是( )
①由图1和图2面积相等可得d=false;
②由AE≥AF可得 false;
③由AD≥AE可得 false;
④由AD≥AF可得a2+b2≥2ab.
其中,正确结论的序号是 .
17.三个同学对问题“已知m,n均为正数,且m+n=1,求false的最小值”提出各自的解题思路:
甲:false=false=2+false,可用基本不等式求解;
乙:false=false=false=false,可用二次函数配方法求解;
丙:false=(false)(m+n)=2+false,可用基本不等式求解.
参考上述解题思路,可求得当x= 时,false(0<x<10,a>0)有最小值 .
三、解答题(解答应写出文字说明,证明过程或演算步骤)
18.(本小题满分14分)已知全集U=R,A={x|-falsex2+x+1>0},B={x|3x2-4x+1>0},求?U(A∩B).
19.(本小题满分15分)(1)若a>0,b>0,a≠b,试比较false+false与false的大小.
(2)已知2<x<3<y<4,求x-y,2x-y,false各自的取值范围.
20.(本小题满分15分)已知x>0,y>0,且2x+8y-xy=0,求:
(1)xy的最小值;
(2)x+y的最小值.
21.(本小题满分15分)已知不等式ax2-3x+2<0的解集为{x|1(1)求实数a,b的值;
(2)解不等式ax2-(ac+b)x+bc≥0(c∈R).
22.(本小题满分15分)如图4所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求点B在AM上,点D在AN上,且对角线MN过点C.已知AB=3米,AD=2米.
(1)要使矩形AMPN的面积大于32平方米,请问AN的长应在什么范围;
(2)当AN的长度是多少时,矩形AMPN的面积最小,并求出最小面积.
阶段检测(二)
一、选择题
1.A 【解析】因为false,所以false,所以false,所以false,false,a<a-b<0.
2.C 【解析】因为false,所以①正确;因为false,false,当a<0,b<0时,a+b≥2false不成立,所以②③④错误.
3. A 【解析】因为x2-2x<0,所以01}∪{x|00},选A.
4. D 【解析】因为x>0,所以false,当且仅当false,即false时,等号成立.
5. A 【解析】因为4x+3y≥2false=4false,所以4false≤12,即xy≤3.当且仅当4x=3y,即x=false,y=2时,等号成立.所以S矩形=xy≤3.
6. A 【解析】因为a+b=ab-1≤false-1,所以(a+b)2-4(a+b)-4≥0,又因为a,b均为正数,所以a+b≥2+2false,当且仅当a=b时等号成立.
7. C 【解析】false,又false,false.
8. A 【解析】若a=b,则(1-a)a>false,即a-a2>false,即a2-a+false<0,即(a-false)2<0,这显然不成立,所以a≠b.若取a=false,b=false,可知题设式子成立;若取a=false,b=false,则不成立.
9. B 【解析】(x+y)(false)=1+a+false≥1+a+2false,当且仅当y=falsex时等号成立,所以1+a+2false≥9,解得a≥4.
10. A 【解析】设购买1千克甲种蔬菜所需费用为x元,购买1千克乙种蔬菜所需费用为y元,由题意得2x+y>8,4x+5y<22,2x=A,3y=B,整理得x=false,y=false,A+false>8, ①2A+falseB<22,②
①×(-2)+②得B<6,将B<6代入A>8-false中,解得A>6,故A>B,故选A.
二、填空题
11.x2+2>3x 【解析】因为x<1,所以x2+2-3x=(x-1)(x-2)>0,即x2+2>3x.
12. 4 7 【解析】由题意得-2+false=-false,(-2)×false=-false,解得a=4,b=7.
13. {x|-2≤x≤1} 【解析】由题意得-x2-x+2≥0,解得{x|-2≤x≤1}.
14.-2 {x|-1<x<3} 【解析】由false的解集为{x|x<-2},得false且false,不等式ax2+bx-3a>0等价于ax2-2ax-3a>0,因为false,所以false,解得-1<x<3,所以关于x的不等式ax2+bx-3a>0的解集为{x|-1<x<3}.
15.false false 【解析】因为实数x,y满足x>y>0,且xy=4,所以false≥2false=false,当且仅当x=2false,y=false时等号成立;false=false=false≤false,当且仅当x=2false+2,y=2false-2时等号成立.
16.①②③④ 【解析】由图1和图2面积相等知ab=(a+b)d,可得d=false,①正确;图3中由面积相等知falseab=falsefalse?AF,所以AF=false,又d=false,则AE=false,所以由AE≥AF可得false≥false,整理得 false,故②正确;又AD=falseBC=falsefalse,由AD≥AE可得falsefalse≥false,整理得 false,故③正确;由AD≥AF可得falsefalse≥false,整理得a2+b2≥2ab,故④正确.
17.false false 【解析】false=(false)[x2+(100-x2)]×false=false[a2+1+false]≥false,当且仅当false,即x=false时,等号成立.
三、解答题
18. 【解析】由于A={x|3x2-4x-4<0}={x|-false0}={x|x则A∩B={x|-false所以?U(A∩B)={x|x≤-false,或false≤x≤1,或x≥2}.
19. 【解析】(1)false+false-false=false+false
=(b-a)(false-false)=(b-a)false
=false,
因为a>0,b>0,a≠b,所以false>0,false>0,false>0,所以false>0,
所以false+false>false.
(2)因为220. 【解析】由2x+8y-xy=0,得false=1.
(1)因为x>0,y>0,所以1=false≥2false=false,所以xy≥64,当且仅当x=16,y=4时,等号成立,
所以xy的最小值为64.
(2)x+y=(false)(x+y)=10+false≥10+2false=18,
当且仅当x=12,y=6时,等号成立,
所以x+y的最小值为18.
21.【解析】(1)因为不等式等式false的解集为false,
所以1和false是方程false的两个实数根.
所以false解得false
(2)由(1)知不等式false,即false,
即false.
当false时,原不等式的解集为false;
当false时,原不等式的解集为false;
当false时,原不等式的解集为false.
22.【解析】设false的长为false米false,则由false,得AM=false,
所以false.
(1)由false,得false.
又false①,所以false②.
从而,由①②联立解得false.
故所求false长度的取值范围是{x|2<x<false或x>8}.
(2)falsefalse,其中false. 又false,
所以false,当且仅当false,即false时,等号成立.
故false的长为4米时,矩形false的面积最小,且最小面积为24平方米.
测试范围:一元二次函数、方程和不等式
选择题部分(共40分)
一、选择题(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1. 若false
2.给出下列不等式:
①a2+3>2a;
②a2+b2>2(a-b-1);
③x2+y2>2xy;
④a+b≥2false.
其中恒成立的不等式的个数为 ( )
A. 3 B. 2 C. 1 D. 0
3. 已知集合A={x|x>1},B={x|x2-2x<0},则A∪B= ( )
A. {x|x>0}B. {x|x>1}C. {x|1
A. 2 B.false C.false D. false
5. 已知矩形的相邻边长x,y满足4x+3y=12,则该矩形面积的最大值为 ( )
A. 3 B. 6 C. 8 D. 9
6. 若正数a,b满足ab-a-b=1,则a+b的最小值为 ( )
A. 2+2false B.2-2false C. -false D.-2false
7. 若关于x的不等式x2-ax-6a2>0(a<0)的解集为{x|x<x1,或x>x2},且x2-x1=5false,则a= ( )
A.- false B. -false C. -false D. -false
8. 若0
A. ab D. a≥b
9. 已知不等式(x+y)(false)≥9对任意正实数x,y恒成立,则正实数a的最小值是 ( )
A. 2 B. 4 C. 6 D. 8
10. 根据对农贸市场蔬菜价格的调查得知,购买2千克甲种蔬菜与1千克乙种蔬菜所需费用之和大于8元,而购买4千克甲种蔬菜与5千克乙种蔬菜所需费用之和小于22元.设购买2千克甲种蔬菜所需费用为A元,购买3千克乙种蔬菜所需费用为B元,则 ( )
A. A>B B. A非选择题部分(共110分)
二、填空题(本大题共7小题,多空题每题6分,单空题每题4分,共36分,把答案填在题中横线上)
11.已知x<1,则x2+2与3x的大小关系是_______.
12. 若不等式ax2+bx-2<0的解集为{x|-2<x<false},则a=____________,b=____________.
13. 使false有意义的x满足____________.
14.已知关于x的不等式false的解集为false,则false____,关于x的不等式ax2+bx-3a>0的解集为_______.
15.已知x>0,y>0,且x+2y=xy,若x+2y>m2+2m恒成立,则xy的最小值为_____,实数m的取值范围为_____.
16.《九章算术》中“勾股容方”问题:“今有勾五步,股十二步,问勾中容方几何?”魏晋时期数学家刘徽在其《九章算术注》中利用出入相补原理给出了这个问题的一般解法:如图1,用对角线将长和宽分别为b和a的矩形分成两个直角三角形,每个直角三角形再分成一个内接正方形(左斜线)和两个小直角三角形(右斜线、灰).将三种颜色的图形进行重组,得到如图2所示的矩形,该矩形长为a+b,宽为内接正方形的边长d.由刘徽构造的图形可以得到许多重要的结论,如图3.设D为斜边BC的中点,作直角三角形ABC的内接正方形对角线AE,过点A作AF⊥BC于点F,则下列推理正确的是( )
①由图1和图2面积相等可得d=false;
②由AE≥AF可得 false;
③由AD≥AE可得 false;
④由AD≥AF可得a2+b2≥2ab.
其中,正确结论的序号是 .
17.三个同学对问题“已知m,n均为正数,且m+n=1,求false的最小值”提出各自的解题思路:
甲:false=false=2+false,可用基本不等式求解;
乙:false=false=false=false,可用二次函数配方法求解;
丙:false=(false)(m+n)=2+false,可用基本不等式求解.
参考上述解题思路,可求得当x= 时,false(0<x<10,a>0)有最小值 .
三、解答题(解答应写出文字说明,证明过程或演算步骤)
18.(本小题满分14分)已知全集U=R,A={x|-falsex2+x+1>0},B={x|3x2-4x+1>0},求?U(A∩B).
19.(本小题满分15分)(1)若a>0,b>0,a≠b,试比较false+false与false的大小.
(2)已知2<x<3<y<4,求x-y,2x-y,false各自的取值范围.
20.(本小题满分15分)已知x>0,y>0,且2x+8y-xy=0,求:
(1)xy的最小值;
(2)x+y的最小值.
21.(本小题满分15分)已知不等式ax2-3x+2<0的解集为{x|1
(2)解不等式ax2-(ac+b)x+bc≥0(c∈R).
22.(本小题满分15分)如图4所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求点B在AM上,点D在AN上,且对角线MN过点C.已知AB=3米,AD=2米.
(1)要使矩形AMPN的面积大于32平方米,请问AN的长应在什么范围;
(2)当AN的长度是多少时,矩形AMPN的面积最小,并求出最小面积.
阶段检测(二)
一、选择题
1.A 【解析】因为false,所以false,所以false,所以false,false,a<a-b<0.
2.C 【解析】因为false,所以①正确;因为false,false,当a<0,b<0时,a+b≥2false不成立,所以②③④错误.
3. A 【解析】因为x2-2x<0,所以0
4. D 【解析】因为x>0,所以false,当且仅当false,即false时,等号成立.
5. A 【解析】因为4x+3y≥2false=4false,所以4false≤12,即xy≤3.当且仅当4x=3y,即x=false,y=2时,等号成立.所以S矩形=xy≤3.
6. A 【解析】因为a+b=ab-1≤false-1,所以(a+b)2-4(a+b)-4≥0,又因为a,b均为正数,所以a+b≥2+2false,当且仅当a=b时等号成立.
7. C 【解析】false,又false,false.
8. A 【解析】若a=b,则(1-a)a>false,即a-a2>false,即a2-a+false<0,即(a-false)2<0,这显然不成立,所以a≠b.若取a=false,b=false,可知题设式子成立;若取a=false,b=false,则不成立.
9. B 【解析】(x+y)(false)=1+a+false≥1+a+2false,当且仅当y=falsex时等号成立,所以1+a+2false≥9,解得a≥4.
10. A 【解析】设购买1千克甲种蔬菜所需费用为x元,购买1千克乙种蔬菜所需费用为y元,由题意得2x+y>8,4x+5y<22,2x=A,3y=B,整理得x=false,y=false,A+false>8, ①2A+falseB<22,②
①×(-2)+②得B<6,将B<6代入A>8-false中,解得A>6,故A>B,故选A.
二、填空题
11.x2+2>3x 【解析】因为x<1,所以x2+2-3x=(x-1)(x-2)>0,即x2+2>3x.
12. 4 7 【解析】由题意得-2+false=-false,(-2)×false=-false,解得a=4,b=7.
13. {x|-2≤x≤1} 【解析】由题意得-x2-x+2≥0,解得{x|-2≤x≤1}.
14.-2 {x|-1<x<3} 【解析】由false的解集为{x|x<-2},得false且false,不等式ax2+bx-3a>0等价于ax2-2ax-3a>0,因为false,所以false,解得-1<x<3,所以关于x的不等式ax2+bx-3a>0的解集为{x|-1<x<3}.
15.false false 【解析】因为实数x,y满足x>y>0,且xy=4,所以false≥2false=false,当且仅当x=2false,y=false时等号成立;false=false=false≤false,当且仅当x=2false+2,y=2false-2时等号成立.
16.①②③④ 【解析】由图1和图2面积相等知ab=(a+b)d,可得d=false,①正确;图3中由面积相等知falseab=falsefalse?AF,所以AF=false,又d=false,则AE=false,所以由AE≥AF可得false≥false,整理得 false,故②正确;又AD=falseBC=falsefalse,由AD≥AE可得falsefalse≥false,整理得 false,故③正确;由AD≥AF可得falsefalse≥false,整理得a2+b2≥2ab,故④正确.
17.false false 【解析】false=(false)[x2+(100-x2)]×false=false[a2+1+false]≥false,当且仅当false,即x=false时,等号成立.
三、解答题
18. 【解析】由于A={x|3x2-4x-4<0}={x|-false
19. 【解析】(1)false+false-false=false+false
=(b-a)(false-false)=(b-a)false
=false,
因为a>0,b>0,a≠b,所以false>0,false>0,false>0,所以false>0,
所以false+false>false.
(2)因为2
(1)因为x>0,y>0,所以1=false≥2false=false,所以xy≥64,当且仅当x=16,y=4时,等号成立,
所以xy的最小值为64.
(2)x+y=(false)(x+y)=10+false≥10+2false=18,
当且仅当x=12,y=6时,等号成立,
所以x+y的最小值为18.
21.【解析】(1)因为不等式等式false的解集为false,
所以1和false是方程false的两个实数根.
所以false解得false
(2)由(1)知不等式false,即false,
即false.
当false时,原不等式的解集为false;
当false时,原不等式的解集为false;
当false时,原不等式的解集为false.
22.【解析】设false的长为false米false,则由false,得AM=false,
所以false.
(1)由false,得false.
又false①,所以false②.
从而,由①②联立解得false.
故所求false长度的取值范围是{x|2<x<false或x>8}.
(2)falsefalse,其中false. 又false,
所以false,当且仅当false,即false时,等号成立.
故false的长为4米时,矩形false的面积最小,且最小面积为24平方米.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
