北师大版九年级下册第三章圆高分突破压轴专练试卷(二)(Word版含答案)
文档属性
| 名称 | 北师大版九年级下册第三章圆高分突破压轴专练试卷(二)(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 298.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-19 00:00:00 | ||
图片预览


文档简介
第三章《圆》高分突破压轴专练(二)
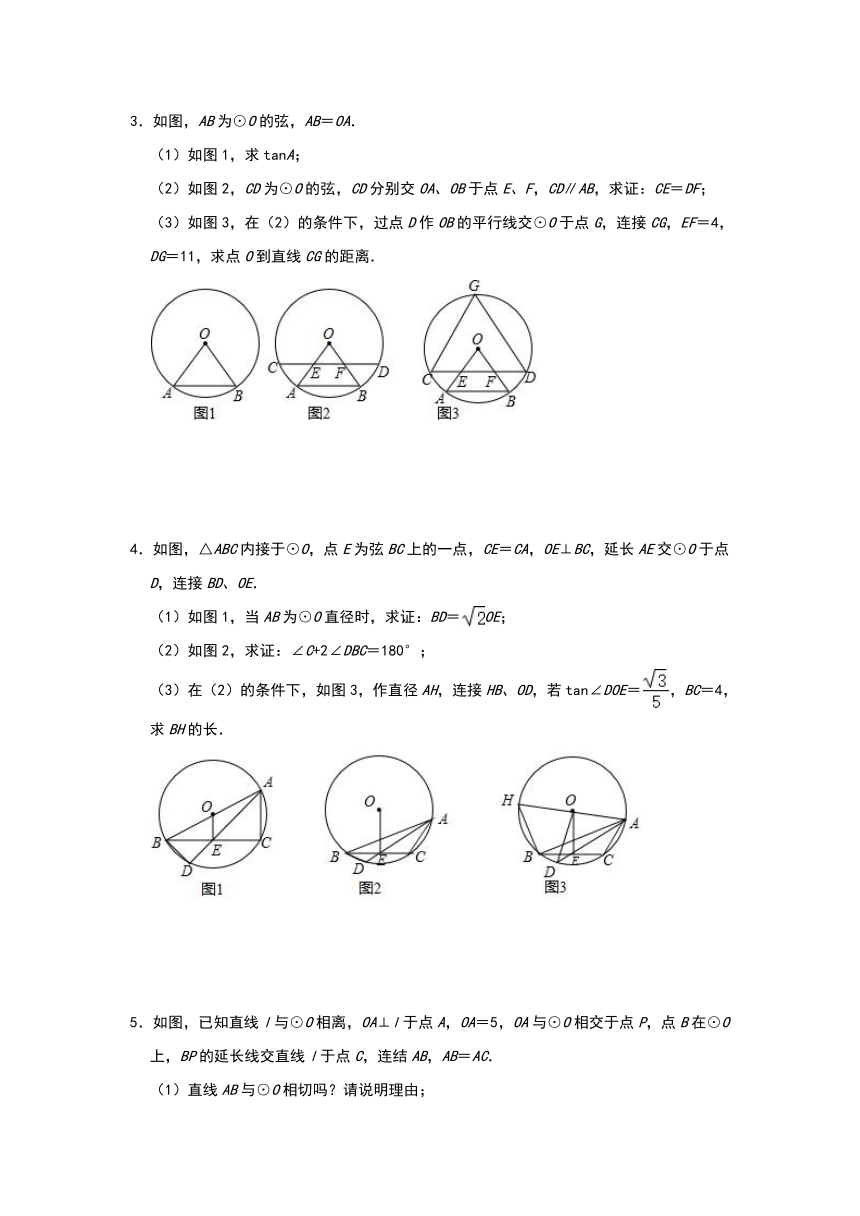
1.如图①,在平面直角坐标系中,直径为2的⊙A经过坐标系原点O(0,0),与x轴交于点B,与y轴交于点C(0,).
(1)求点B的坐标;
(2)如图②,过点B作⊙A的切线交直线OA于点P,求点P的坐标;
(3)过点P作⊙A的另一条切线PE,请直接写出切点E的坐标.
2.如图,已知△ABC是等边三角形,以AB为直径作⊙O,交BC边于点D,交AC边于点F,作DE⊥AC于点E.
(1)求证:DE是⊙O的切线;
(2)若△ABC的边长为4,求EF的长度.
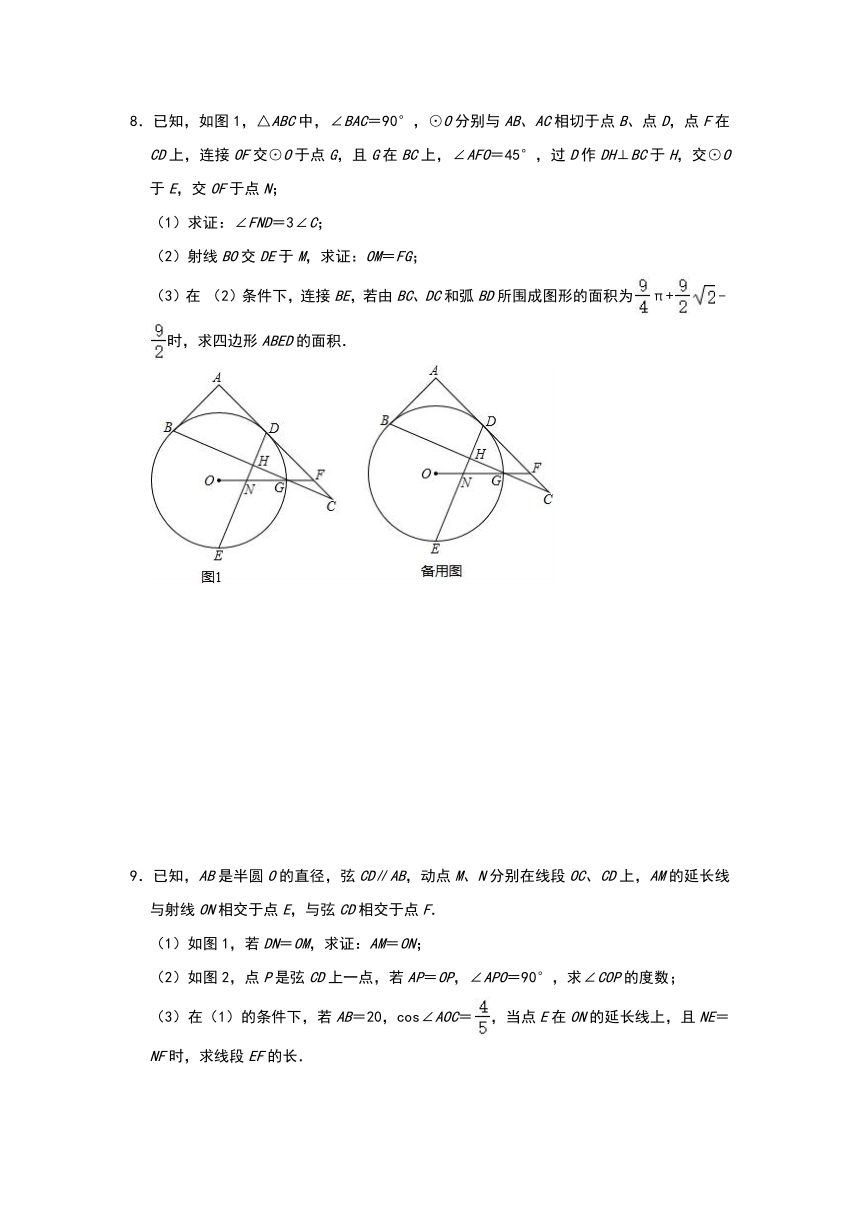
3.如图,AB为⊙O的弦,AB=OA.
(1)如图1,求tanA;
(2)如图2,CD为⊙O的弦,CD分别交OA、OB于点E、F,CD∥AB,求证:CE=DF;
(3)如图3,在(2)的条件下,过点D作OB的平行线交⊙O于点G,连接CG,EF=4,DG=11,求点O到直线CG的距离.
4.如图,△ABC内接于⊙O,点E为弦BC上的一点,CE=CA,OE⊥BC,延长AE交⊙O于点D,连接BD、OE.
(1)如图1,当AB为⊙O直径时,求证:BD=OE;
(2)如图2,求证:∠C+2∠DBC=180°;
(3)在(2)的条件下,如图3,作直径AH,连接HB、OD,若tan∠DOE=,BC=4,求BH的长.
5.如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA与⊙O相交于点P,点B在⊙O上,BP的延长线交直线l于点C,连结AB,AB=AC.
(1)直线AB与⊙O相切吗?请说明理由;
(2)线段BC的中点为M,当⊙O的半径r为多少时,直线AM与⊙O相切.
6.如图PA、PB分别切⊙O于点A、B,线段PO交⊙O于点D,AO的延长线交⊙O于点C,过点P作PM∥AC交CB的延长线于点M.
(1)求证:四边形POCM是平行四边形;
(2)若△PAB为等边三角形,判断点A、D、M是否在同一条直线上并说明理由;
(3)若线段PA、PD长是方程x2﹣6x+8=0的两个根,求平行四边形POCM的面积.
7.如图,AB是⊙O的直径,点C在⊙O上,CD⊥AB于D,AD=2,CD=4.∠BCD的角平分线CE与过点B的切线l交过点E.
(1)求⊙O半径的长;
(2)求点E到直线BC的距离.
8.已知,如图1,△ABC中,∠BAC=90°,⊙O分别与AB、AC相切于点B、点D,点F在CD上,连接OF交⊙O于点G,且G在BC上,∠AFO=45°,过D作DH⊥BC于H,交⊙O于E,交OF于点N;
(1)求证:∠FND=3∠C;
(2)射线BO交DE于M,求证:OM=FG;
(3)在
(2)条件下,连接BE,若由BC、DC和弧BD所围成图形的面积为π+﹣时,求四边形ABED的面积.
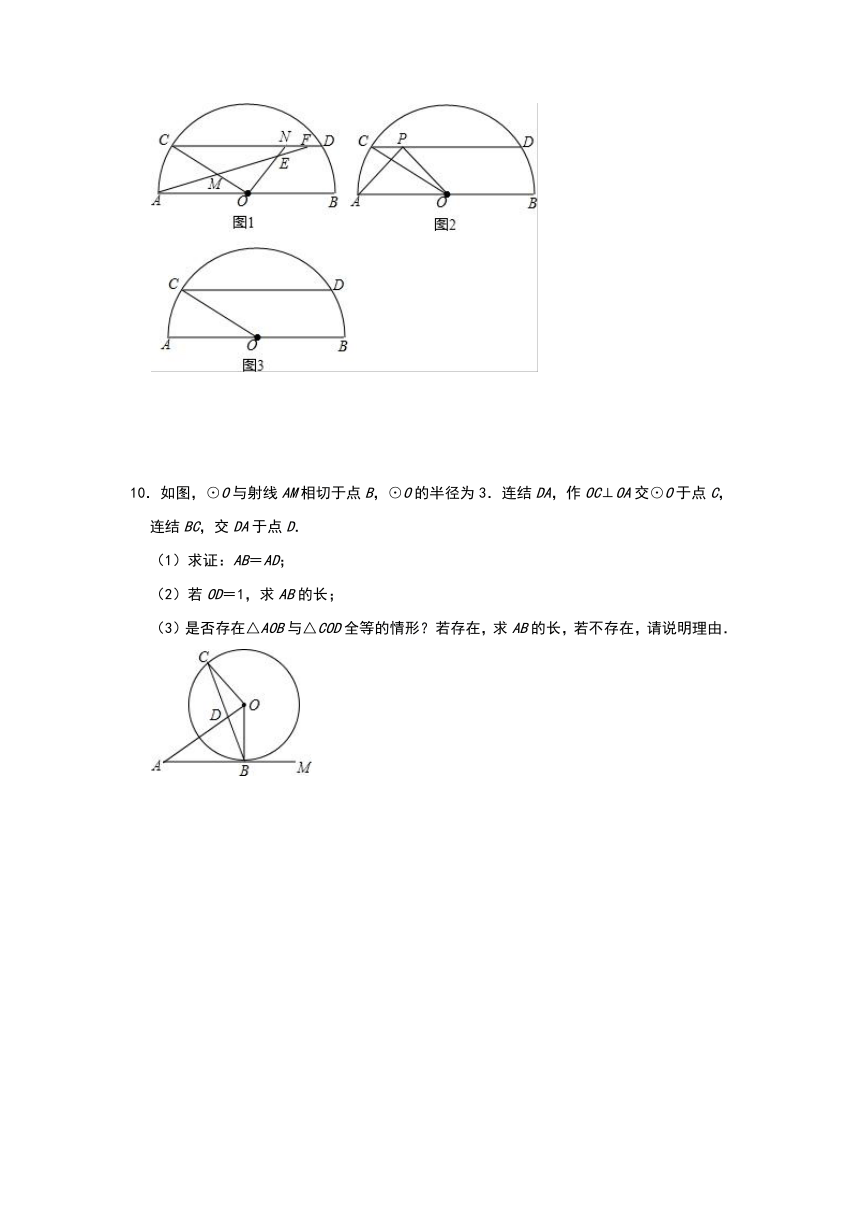
9.已知,AB是半圆O的直径,弦CD∥AB,动点M、N分别在线段OC、CD上,AM的延长线与射线ON相交于点E,与弦CD相交于点F.
(1)如图1,若DN=OM,求证:AM=ON;
(2)如图2,点P是弦CD上一点,若AP=OP,∠APO=90°,求∠COP的度数;
(3)在(1)的条件下,若AB=20,cos∠AOC=,当点E在ON的延长线上,且NE=NF时,求线段EF的长.
10.如图,⊙O与射线AM相切于点B,⊙O的半径为3.连结DA,作OC⊥OA交⊙O于点C,连结BC,交DA于点D.
(1)求证:AB=AD;
(2)若OD=1,求AB的长;
(3)是否存在△AOB与△COD全等的情形?若存在,求AB的长,若不存在,请说明理由.
参考答案
1.解:(1)如图①,连接BC,
∵∠BOC=90°,
∴BC是⊙A的直径,
∴,
∵,
∴.
∴OB==3,
∴B(3,0);
(2)如图②,过点P作PD⊥x轴于点D,
∵PB为⊙A的切线,
,
∴.
∴∠OBC=30°,
∴∠AOB=30°.
∴∠OPB=180°﹣∠POB﹣∠ABO﹣∠ABP=30°.
∴OB=BP=3,
在Rt△PBD中,∠PDB=90°,∠PBD=60°,BP=3,
∴,.
∵OB=3,
∴.
∴;
(3)由(2)得,∠OPB=30°,
∵PE、PB是⊙A的切线,
∴∠EPA=∠OPB=30°,
∴∠EPB=60°,又∠PBD=60°,
∴PE∥OD,
∴.
2.(1)证明:如图1,连接OD,
∵△ABC是等边三角形,
∴∠B=∠C=60°.
∵OB=OD,
∴∠ODB=∠B=60°.
∵DE⊥AC,
∴∠DEC=90°.
∴∠EDC=30°.
∴∠ODE=90°.
∴DE⊥OD于点D.
∵点D在⊙O上,
∴DE是⊙O的切线;
(2)解:如图2,连接AD,BF,
∵AB为⊙O直径,
∴∠AFB=∠ADB=90°.
∴AF⊥BF,AD⊥BD.
∵△ABC是等边三角形,
∴,.
∵∠EDC=30°,
∴.
∴FE=FC﹣EC=1.
3.解:(1)如图1中,
∵OA=OB,AB=OA,
∴OA=OB=AB,
∴△OAB是等边三角形,
∴∠A=60°,
∴tanA=.
(2)如图2中,作OK⊥CD于K.
∵OK⊥CD,
∴CK=KD,
∵CD∥AB,
∴∠OEF=∠A=60°=∠AOB,
∴△OEF是等边三角形,
∴OE=OF,∵OK⊥EF,
∴KE=KF,
∴CK﹣KE=KD﹣KF,即CE=DF.
(3)如图3中,作OH⊥CD于K,FK⊥DG于K,GN⊥CD于N,OJ⊥CD于J,OM⊥CG于M.
∵△OEF是等边三角形,
∴EF=OF=OE=4,
∵∠OHK=∠FKH=90°,
∵DG∥OB,
∴∠HOF+∠OHK=180°,
∴∠HOF=90°,
∴∠OHK=∠FKH=∠HOF=90°,
∴四边形OFKH是矩形,设OH=x,
∴HK=OF=4,OH=FK=x,KD=x,
∵OH⊥DG,DG=11,
∴DH=GH=,
∴4+x=,
∴x=,
∴OD===,
∴JD=CJ===5,CD=2JD=10,
在Rt△GND中,∵DG=11,∠GDN=60°,∠GND=90°,
∴DN=,GN=,CN=CD﹣DN=,
在Rt△CGN中,CG===,
∵S△COG+S△COD+S△DOG=S△CDG,
∴?OM+?10?2+?11?=?10?,
∴OM=.
4.解:(1)如图1中,
∵OE⊥BC,
∴BE=EC.
∵OA=OB,
∴OE=AC.
∵AB为直径,
∴∠ADB=∠ACB=90°.
∵AC=CE,
∴∠CAE=∠BED=45°.
∵sin∠BED==,
∴BE=CE=AC=BD,
∴BD=OE.
(2)如图2中,
∵AC=CE,
∴∠CAE=∠CEA,
∵∠DBC=∠EAC,
∴∠DBC+∠CEA+∠ACB=180°,
∴∠C+2∠DBC=180°;
(3)解:如图3,过点O作OM⊥AC于点M,过点D作DK⊥BC于点K、DG⊥OE交OE延长线于点G,连接OC,过点A作AP⊥BC交BC延长线于点P.
由(2)得:BE=CE=AC=BC=2,
∵OA=OC,
∴AM=CM=1,
∵BD=DE,
∴BK=KE=1,
∵∠DKE=∠DGE=∠GEK=90°,四边形DKEG为矩形,
∴DG=1,
∵OA=OD,
∴△OAM≌△ODG,
∴∠DOG=∠AOM,
∴tan∠AOM=tan∠DOG==,
∵AM=1,
∴OM=,
∴OA==,
∴AH=2OA=,
∵∠AOC=2∠ABC,
∴∠ABC=∠AOM,
∵tan∠ABC=tan∠AOM==,
设AP=a,BP=5a,
∴CP=5a﹣4,
∵AP2+CP2=AC2,即(a)2+(5a﹣4)2=22,
解得:a1=1,a2=(舍去),
∴BP=5,AP=,AB==2,
∴BH==.
5.解:(1)直线AB与⊙O相切.理由如下:
连接OB,如图,
∵AB=AC,
∴∠ABC=∠ACB,
又∵OP=OB,
∴∠OPB=∠OBP,
∵OA⊥l,
∴∠OAC=90°,
∴∠ACB+∠APC=90°.
而∠ABC=∠ACB,∠APC=∠OPB=∠OBP,
∴∠OBP+∠ABC=90°,即∠OBA=90°,
∴OB⊥AB,
∴直线AB是⊙O的切线;
(2)设AM与⊙O切于点T,连接OT,如图,
∵AB和AT为切线,
∴∠OAT=∠OAB,
∵M点为BC的中点,
而AB=AC,
∴∠CAM=∠BAM,
∴∠CAM=2∠OAT,
而∠CAO=90,
∴∠OAT=30°,
∴OT=OA=.
6.解:(1)∵PA、PB分别切⊙O于点A、B,线段PO交⊙O于点D,
∴PO⊥AB,
∵AC是⊙O的直径,
∴∠ABC=∠ABM=90°,
∴PO∥MC,
∵PM∥AC,
∴四边形POCM是平行四边形;
(2)在,
理由:如图,连接AD,CD,DM,
∵△PAB为等边三角形,
∴∠APO=30°,
∵PA是⊙O的切线,
∴∠PAO=90°,
∴∠AOD=60°,
∵AC是⊙O直径,
∴∠ADC=90°,
∠OCD=30°,
∵OA=OD=OC,
∴∠ODC=∠OCD=30°,
∵AC∥PM,
∴∠OPM=∠AOD=60°
∵PO∥MC,
∴∠DCM=∠ODC=30°,
在Rt△AOP中,∠APO=30°,
∴PO=2OA=2OD=2OC,
∴PD=OC,
由(1)知,四边形POCM是平行四边形,
∴∠POC=∠PMC=120°,OC=CM,
∴PD=CM,
∴∠PMD=∠PDM=60°,
∴∠DMC=60°,
∴∠DMC+∠DCM=60°+30°=90°,
∴∠CDM=90°,
∵∠ADC=90°,
∴点A、D、M在同一条直线上.
(3)如图1,
∵线段PA、PD长是方程x2﹣6x+8=0的两个根,
∴PA=4,PD=2,
根据切割线定理得,PA2=PD(PD+AC),
∴16=2(2+AC),
∴AC=6,
∴OA=OD=3,
∴PO=PD+OD=5,
根据等面积法得,PA×OA=AF×PO,
∴4×3=AF×5,
∴AF=,
∴S平行四边形POCM=PO×BF=PO×AF=5×=12.
7.解:(1)如图1中,连接OC,设⊙O的半径为r.
∵AD=2,OD=r﹣2,
∵CD⊥AB,
∴∠CDO=90°,
在Rt△CDO中,∵CD2+DO2=CO2,
∴42+(r﹣2)2=r2,
∴r=5,
⊙O的半径为5.
(2)如图2中,过点E作EF⊥CD,垂足为点F,EG⊥CB,垂足为G,则∠EFD=90°,
∵直线l切⊙O于B,
∴AB⊥l,
∴∠DBE=90°,
∵CD⊥AB,
∴∠BDF=90°,
∴四边形BDFE是矩形,
∴EF=BO+OD=8,
∵点E在∠BCD的平分线上,
∴EG=EF=8.
∴点E到直线BC的距离为8.
8.解:(1)如图1,
∵∠BAC=90°,
∴∠C+∠ABC=90°,
连接OB,OD,
∵⊙O分别与AB、AC相切于点B、点D,
∴∠ABO=∠ADO=90°,
∴∠OBC+∠ABC=90°,
∴∠OBC=∠C,
∵∠ODC=90°,∠AFO=45°,
∴∠DOF=45°
∵∠BAD=90°,
∴四边形ABOD是矩形,
∴∠BOD=90°,
∴∠BOG=∠BOD+∠DOF=135°,
∵OB=OG,
∴∠OBG=∠OGB=22.5°,
∴∠C=∠OBC=22.5°,
在四边形ABHD中,
∵DH⊥BC,
∴∠BHD=90°,
∵∠A=90°,
∴∠ABH+∠ADH=180°,
∴∠ABO﹣∠OBC+∠ADO+∠ODN=180°,
∵∠ABO=∠ADO=90°,
∴∠ODN=∠OBC=22.5°,
∴∠DNF=∠DOF+∠ODN=45°+22.5°=67.5°,
∵∠C=22.5°,
∴∠FDN=3∠C,
(2)如图2,
由(1)知,∠ODN=22.5°,
∴∠FDN=67.5°=∠DNF,
∴FN=FD,
在Rt△ODF中,∠AFO=45°,
∴FD=OD=OG=ON+NG,
∵FN=ON+NG,
∴FG=ON,
∵∠BOF=135°,
∴∠MON=45°,
∵∠ONM=∠DNF=67.5°,
∴∠OMN=67.5°,
∴OM=ON,
∴OM=FG,
(3)如图3,设⊙O的半径为R,
∴AB=AD=OB=R,
∴BD=OB=R,
由(2)知,∠CDH=67.5°,
由(1)知,∠ODN=22.5°,
∵∠ODB=45°,
∴∠BDH=67.5°,
∴∠BDH=∠CDH,
∵DH⊥BC,
∴CD=BD=R,
∴AC=AD+CD=(+1)R,
∵BD是正方形ABOD的对角线,
∴S△ABD=S△OBD
∵由BC、DC和弧BD所围成图形的面积为π+﹣,
∴π+﹣=S△ABC﹣S△ABD+S弓形BD
=S△ABC﹣S△ABD+S扇形OBD﹣S△BDO=S△ABC+S扇形OBD﹣2S△BDO=AB×AC+﹣2×OB2=R×(+1)R+﹣R2=(﹣+)R2,
∴R=3,
∵∠BDE=67.5°,∠E=∠BOD=45°,
∴∠EBD=67.5°=∠BDE,
∴BE=DE,
∵OB=OD,
∴点O,E都在BD的垂直平分线上,
∴△BDE的边BD上的高h=R+,
∴S四边形ABED=S△ABD+S△BDE=×+=(1+)R2=9+.
9.解:(1)如图1,
连接OD,
∴OA=OD,
∵CD∥AB,
∴∠BOD=∠NDO,,
∴∠AOC=∠BCD,
∴∠AOC=∠CDO,
在△AMO和△OND中,,
∴△AMO≌△OND,
∴AM=ON,
(2)如图2,
过点C作CG⊥AB,PH⊥AB,
∴CG=PH,
∵AP=OP,∠APO=90°,
∴∠AOP=45°,PH=OA,
∴CG=OA=OC,
∴∠AOC=30°,
∴∠COP=∠AOP﹣∠AOC=15°.
(3)如图3,
作OG⊥CD于G,连接OD,
∵AB=20,
∴OC=10
CG=OC?cos∠C=OC?cos∠AOC=10×=8
∴CD=2CG=16
∵NE=NF,
∴∠E=∠EFN
∵CD∥AB,
∴∠EFN=∠A
∴∠E=∠A,
∴OE=OA
∵CD∥AB,
∴∠BOD=∠D=∠C=∠AOC
∴∠AOE=∠COD
∴△AOE≌△COD,
∴AE=CD=16
∵△AOM≌△ODN,
∴∠NOD=∠A=∠E
∴AE∥OD,
∴四边形AODF是平行四边形
∴AF=OD=10
∴EF=AE﹣AF=16﹣10=6,
10.解:(1)∵OB=OC,
∴∠OCB=∠OBC,
∵OC⊥OA,
∴∠OCB+∠ODC=90°,
∴∠OBC+∠ODC=90°,
∵∠ADB=∠ODC,
∴∠OBC+∠ADB=90°,
∵⊙O与射线AM相切于点B,
∴∠ABO=90°,
∴∠OBC+∠ABD=90°,
∴∠ABD=∠ADB,
∴AB=AD;
(2)由(1)知,AB=AD,
∴OA=AD+OD=AD+1,
在Rt△ABO中,AB2+OB2=OA2,
AD2+9=(AD+1)2,
∴AB=AD=4;
(3)存在,
理由:∵△AOB和△COD都是直角三角形,
∴△AOB与△COD全等,
只有AB=OC或AB=OD,
①当AB=OC时,
∵OB=OC,
∴AB=OB=3,
∴∠A=∠AOB=45°,
∵AB=AD,
∴∠ODC=∠ADB=67.5°≠∠AOB,
∴此种情况不存在,
②当AB=OD时,
∵AD=AB,
∴AD=OD,即:OA=2AD=2AB,
在Rt△ABO中,OB=3,
根据勾股定理得,AB2+OB2=AD2,
∴AB2+9=4AB2,
∴AB=
即:存在△AOB与△COD全等,此时AB=.
1.如图①,在平面直角坐标系中,直径为2的⊙A经过坐标系原点O(0,0),与x轴交于点B,与y轴交于点C(0,).
(1)求点B的坐标;
(2)如图②,过点B作⊙A的切线交直线OA于点P,求点P的坐标;
(3)过点P作⊙A的另一条切线PE,请直接写出切点E的坐标.
2.如图,已知△ABC是等边三角形,以AB为直径作⊙O,交BC边于点D,交AC边于点F,作DE⊥AC于点E.
(1)求证:DE是⊙O的切线;
(2)若△ABC的边长为4,求EF的长度.
3.如图,AB为⊙O的弦,AB=OA.
(1)如图1,求tanA;
(2)如图2,CD为⊙O的弦,CD分别交OA、OB于点E、F,CD∥AB,求证:CE=DF;
(3)如图3,在(2)的条件下,过点D作OB的平行线交⊙O于点G,连接CG,EF=4,DG=11,求点O到直线CG的距离.
4.如图,△ABC内接于⊙O,点E为弦BC上的一点,CE=CA,OE⊥BC,延长AE交⊙O于点D,连接BD、OE.
(1)如图1,当AB为⊙O直径时,求证:BD=OE;
(2)如图2,求证:∠C+2∠DBC=180°;
(3)在(2)的条件下,如图3,作直径AH,连接HB、OD,若tan∠DOE=,BC=4,求BH的长.
5.如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA与⊙O相交于点P,点B在⊙O上,BP的延长线交直线l于点C,连结AB,AB=AC.
(1)直线AB与⊙O相切吗?请说明理由;
(2)线段BC的中点为M,当⊙O的半径r为多少时,直线AM与⊙O相切.
6.如图PA、PB分别切⊙O于点A、B,线段PO交⊙O于点D,AO的延长线交⊙O于点C,过点P作PM∥AC交CB的延长线于点M.
(1)求证:四边形POCM是平行四边形;
(2)若△PAB为等边三角形,判断点A、D、M是否在同一条直线上并说明理由;
(3)若线段PA、PD长是方程x2﹣6x+8=0的两个根,求平行四边形POCM的面积.
7.如图,AB是⊙O的直径,点C在⊙O上,CD⊥AB于D,AD=2,CD=4.∠BCD的角平分线CE与过点B的切线l交过点E.
(1)求⊙O半径的长;
(2)求点E到直线BC的距离.
8.已知,如图1,△ABC中,∠BAC=90°,⊙O分别与AB、AC相切于点B、点D,点F在CD上,连接OF交⊙O于点G,且G在BC上,∠AFO=45°,过D作DH⊥BC于H,交⊙O于E,交OF于点N;
(1)求证:∠FND=3∠C;
(2)射线BO交DE于M,求证:OM=FG;
(3)在
(2)条件下,连接BE,若由BC、DC和弧BD所围成图形的面积为π+﹣时,求四边形ABED的面积.
9.已知,AB是半圆O的直径,弦CD∥AB,动点M、N分别在线段OC、CD上,AM的延长线与射线ON相交于点E,与弦CD相交于点F.
(1)如图1,若DN=OM,求证:AM=ON;
(2)如图2,点P是弦CD上一点,若AP=OP,∠APO=90°,求∠COP的度数;
(3)在(1)的条件下,若AB=20,cos∠AOC=,当点E在ON的延长线上,且NE=NF时,求线段EF的长.
10.如图,⊙O与射线AM相切于点B,⊙O的半径为3.连结DA,作OC⊥OA交⊙O于点C,连结BC,交DA于点D.
(1)求证:AB=AD;
(2)若OD=1,求AB的长;
(3)是否存在△AOB与△COD全等的情形?若存在,求AB的长,若不存在,请说明理由.
参考答案
1.解:(1)如图①,连接BC,
∵∠BOC=90°,
∴BC是⊙A的直径,
∴,
∵,
∴.
∴OB==3,
∴B(3,0);
(2)如图②,过点P作PD⊥x轴于点D,
∵PB为⊙A的切线,
,
∴.
∴∠OBC=30°,
∴∠AOB=30°.
∴∠OPB=180°﹣∠POB﹣∠ABO﹣∠ABP=30°.
∴OB=BP=3,
在Rt△PBD中,∠PDB=90°,∠PBD=60°,BP=3,
∴,.
∵OB=3,
∴.
∴;
(3)由(2)得,∠OPB=30°,
∵PE、PB是⊙A的切线,
∴∠EPA=∠OPB=30°,
∴∠EPB=60°,又∠PBD=60°,
∴PE∥OD,
∴.
2.(1)证明:如图1,连接OD,
∵△ABC是等边三角形,
∴∠B=∠C=60°.
∵OB=OD,
∴∠ODB=∠B=60°.
∵DE⊥AC,
∴∠DEC=90°.
∴∠EDC=30°.
∴∠ODE=90°.
∴DE⊥OD于点D.
∵点D在⊙O上,
∴DE是⊙O的切线;
(2)解:如图2,连接AD,BF,
∵AB为⊙O直径,
∴∠AFB=∠ADB=90°.
∴AF⊥BF,AD⊥BD.
∵△ABC是等边三角形,
∴,.
∵∠EDC=30°,
∴.
∴FE=FC﹣EC=1.
3.解:(1)如图1中,
∵OA=OB,AB=OA,
∴OA=OB=AB,
∴△OAB是等边三角形,
∴∠A=60°,
∴tanA=.
(2)如图2中,作OK⊥CD于K.
∵OK⊥CD,
∴CK=KD,
∵CD∥AB,
∴∠OEF=∠A=60°=∠AOB,
∴△OEF是等边三角形,
∴OE=OF,∵OK⊥EF,
∴KE=KF,
∴CK﹣KE=KD﹣KF,即CE=DF.
(3)如图3中,作OH⊥CD于K,FK⊥DG于K,GN⊥CD于N,OJ⊥CD于J,OM⊥CG于M.
∵△OEF是等边三角形,
∴EF=OF=OE=4,
∵∠OHK=∠FKH=90°,
∵DG∥OB,
∴∠HOF+∠OHK=180°,
∴∠HOF=90°,
∴∠OHK=∠FKH=∠HOF=90°,
∴四边形OFKH是矩形,设OH=x,
∴HK=OF=4,OH=FK=x,KD=x,
∵OH⊥DG,DG=11,
∴DH=GH=,
∴4+x=,
∴x=,
∴OD===,
∴JD=CJ===5,CD=2JD=10,
在Rt△GND中,∵DG=11,∠GDN=60°,∠GND=90°,
∴DN=,GN=,CN=CD﹣DN=,
在Rt△CGN中,CG===,
∵S△COG+S△COD+S△DOG=S△CDG,
∴?OM+?10?2+?11?=?10?,
∴OM=.
4.解:(1)如图1中,
∵OE⊥BC,
∴BE=EC.
∵OA=OB,
∴OE=AC.
∵AB为直径,
∴∠ADB=∠ACB=90°.
∵AC=CE,
∴∠CAE=∠BED=45°.
∵sin∠BED==,
∴BE=CE=AC=BD,
∴BD=OE.
(2)如图2中,
∵AC=CE,
∴∠CAE=∠CEA,
∵∠DBC=∠EAC,
∴∠DBC+∠CEA+∠ACB=180°,
∴∠C+2∠DBC=180°;
(3)解:如图3,过点O作OM⊥AC于点M,过点D作DK⊥BC于点K、DG⊥OE交OE延长线于点G,连接OC,过点A作AP⊥BC交BC延长线于点P.
由(2)得:BE=CE=AC=BC=2,
∵OA=OC,
∴AM=CM=1,
∵BD=DE,
∴BK=KE=1,
∵∠DKE=∠DGE=∠GEK=90°,四边形DKEG为矩形,
∴DG=1,
∵OA=OD,
∴△OAM≌△ODG,
∴∠DOG=∠AOM,
∴tan∠AOM=tan∠DOG==,
∵AM=1,
∴OM=,
∴OA==,
∴AH=2OA=,
∵∠AOC=2∠ABC,
∴∠ABC=∠AOM,
∵tan∠ABC=tan∠AOM==,
设AP=a,BP=5a,
∴CP=5a﹣4,
∵AP2+CP2=AC2,即(a)2+(5a﹣4)2=22,
解得:a1=1,a2=(舍去),
∴BP=5,AP=,AB==2,
∴BH==.
5.解:(1)直线AB与⊙O相切.理由如下:
连接OB,如图,
∵AB=AC,
∴∠ABC=∠ACB,
又∵OP=OB,
∴∠OPB=∠OBP,
∵OA⊥l,
∴∠OAC=90°,
∴∠ACB+∠APC=90°.
而∠ABC=∠ACB,∠APC=∠OPB=∠OBP,
∴∠OBP+∠ABC=90°,即∠OBA=90°,
∴OB⊥AB,
∴直线AB是⊙O的切线;
(2)设AM与⊙O切于点T,连接OT,如图,
∵AB和AT为切线,
∴∠OAT=∠OAB,
∵M点为BC的中点,
而AB=AC,
∴∠CAM=∠BAM,
∴∠CAM=2∠OAT,
而∠CAO=90,
∴∠OAT=30°,
∴OT=OA=.
6.解:(1)∵PA、PB分别切⊙O于点A、B,线段PO交⊙O于点D,
∴PO⊥AB,
∵AC是⊙O的直径,
∴∠ABC=∠ABM=90°,
∴PO∥MC,
∵PM∥AC,
∴四边形POCM是平行四边形;
(2)在,
理由:如图,连接AD,CD,DM,
∵△PAB为等边三角形,
∴∠APO=30°,
∵PA是⊙O的切线,
∴∠PAO=90°,
∴∠AOD=60°,
∵AC是⊙O直径,
∴∠ADC=90°,
∠OCD=30°,
∵OA=OD=OC,
∴∠ODC=∠OCD=30°,
∵AC∥PM,
∴∠OPM=∠AOD=60°
∵PO∥MC,
∴∠DCM=∠ODC=30°,
在Rt△AOP中,∠APO=30°,
∴PO=2OA=2OD=2OC,
∴PD=OC,
由(1)知,四边形POCM是平行四边形,
∴∠POC=∠PMC=120°,OC=CM,
∴PD=CM,
∴∠PMD=∠PDM=60°,
∴∠DMC=60°,
∴∠DMC+∠DCM=60°+30°=90°,
∴∠CDM=90°,
∵∠ADC=90°,
∴点A、D、M在同一条直线上.
(3)如图1,
∵线段PA、PD长是方程x2﹣6x+8=0的两个根,
∴PA=4,PD=2,
根据切割线定理得,PA2=PD(PD+AC),
∴16=2(2+AC),
∴AC=6,
∴OA=OD=3,
∴PO=PD+OD=5,
根据等面积法得,PA×OA=AF×PO,
∴4×3=AF×5,
∴AF=,
∴S平行四边形POCM=PO×BF=PO×AF=5×=12.
7.解:(1)如图1中,连接OC,设⊙O的半径为r.
∵AD=2,OD=r﹣2,
∵CD⊥AB,
∴∠CDO=90°,
在Rt△CDO中,∵CD2+DO2=CO2,
∴42+(r﹣2)2=r2,
∴r=5,
⊙O的半径为5.
(2)如图2中,过点E作EF⊥CD,垂足为点F,EG⊥CB,垂足为G,则∠EFD=90°,
∵直线l切⊙O于B,
∴AB⊥l,
∴∠DBE=90°,
∵CD⊥AB,
∴∠BDF=90°,
∴四边形BDFE是矩形,
∴EF=BO+OD=8,
∵点E在∠BCD的平分线上,
∴EG=EF=8.
∴点E到直线BC的距离为8.
8.解:(1)如图1,
∵∠BAC=90°,
∴∠C+∠ABC=90°,
连接OB,OD,
∵⊙O分别与AB、AC相切于点B、点D,
∴∠ABO=∠ADO=90°,
∴∠OBC+∠ABC=90°,
∴∠OBC=∠C,
∵∠ODC=90°,∠AFO=45°,
∴∠DOF=45°
∵∠BAD=90°,
∴四边形ABOD是矩形,
∴∠BOD=90°,
∴∠BOG=∠BOD+∠DOF=135°,
∵OB=OG,
∴∠OBG=∠OGB=22.5°,
∴∠C=∠OBC=22.5°,
在四边形ABHD中,
∵DH⊥BC,
∴∠BHD=90°,
∵∠A=90°,
∴∠ABH+∠ADH=180°,
∴∠ABO﹣∠OBC+∠ADO+∠ODN=180°,
∵∠ABO=∠ADO=90°,
∴∠ODN=∠OBC=22.5°,
∴∠DNF=∠DOF+∠ODN=45°+22.5°=67.5°,
∵∠C=22.5°,
∴∠FDN=3∠C,
(2)如图2,
由(1)知,∠ODN=22.5°,
∴∠FDN=67.5°=∠DNF,
∴FN=FD,
在Rt△ODF中,∠AFO=45°,
∴FD=OD=OG=ON+NG,
∵FN=ON+NG,
∴FG=ON,
∵∠BOF=135°,
∴∠MON=45°,
∵∠ONM=∠DNF=67.5°,
∴∠OMN=67.5°,
∴OM=ON,
∴OM=FG,
(3)如图3,设⊙O的半径为R,
∴AB=AD=OB=R,
∴BD=OB=R,
由(2)知,∠CDH=67.5°,
由(1)知,∠ODN=22.5°,
∵∠ODB=45°,
∴∠BDH=67.5°,
∴∠BDH=∠CDH,
∵DH⊥BC,
∴CD=BD=R,
∴AC=AD+CD=(+1)R,
∵BD是正方形ABOD的对角线,
∴S△ABD=S△OBD
∵由BC、DC和弧BD所围成图形的面积为π+﹣,
∴π+﹣=S△ABC﹣S△ABD+S弓形BD
=S△ABC﹣S△ABD+S扇形OBD﹣S△BDO=S△ABC+S扇形OBD﹣2S△BDO=AB×AC+﹣2×OB2=R×(+1)R+﹣R2=(﹣+)R2,
∴R=3,
∵∠BDE=67.5°,∠E=∠BOD=45°,
∴∠EBD=67.5°=∠BDE,
∴BE=DE,
∵OB=OD,
∴点O,E都在BD的垂直平分线上,
∴△BDE的边BD上的高h=R+,
∴S四边形ABED=S△ABD+S△BDE=×+=(1+)R2=9+.
9.解:(1)如图1,
连接OD,
∴OA=OD,
∵CD∥AB,
∴∠BOD=∠NDO,,
∴∠AOC=∠BCD,
∴∠AOC=∠CDO,
在△AMO和△OND中,,
∴△AMO≌△OND,
∴AM=ON,
(2)如图2,
过点C作CG⊥AB,PH⊥AB,
∴CG=PH,
∵AP=OP,∠APO=90°,
∴∠AOP=45°,PH=OA,
∴CG=OA=OC,
∴∠AOC=30°,
∴∠COP=∠AOP﹣∠AOC=15°.
(3)如图3,
作OG⊥CD于G,连接OD,
∵AB=20,
∴OC=10
CG=OC?cos∠C=OC?cos∠AOC=10×=8
∴CD=2CG=16
∵NE=NF,
∴∠E=∠EFN
∵CD∥AB,
∴∠EFN=∠A
∴∠E=∠A,
∴OE=OA
∵CD∥AB,
∴∠BOD=∠D=∠C=∠AOC
∴∠AOE=∠COD
∴△AOE≌△COD,
∴AE=CD=16
∵△AOM≌△ODN,
∴∠NOD=∠A=∠E
∴AE∥OD,
∴四边形AODF是平行四边形
∴AF=OD=10
∴EF=AE﹣AF=16﹣10=6,
10.解:(1)∵OB=OC,
∴∠OCB=∠OBC,
∵OC⊥OA,
∴∠OCB+∠ODC=90°,
∴∠OBC+∠ODC=90°,
∵∠ADB=∠ODC,
∴∠OBC+∠ADB=90°,
∵⊙O与射线AM相切于点B,
∴∠ABO=90°,
∴∠OBC+∠ABD=90°,
∴∠ABD=∠ADB,
∴AB=AD;
(2)由(1)知,AB=AD,
∴OA=AD+OD=AD+1,
在Rt△ABO中,AB2+OB2=OA2,
AD2+9=(AD+1)2,
∴AB=AD=4;
(3)存在,
理由:∵△AOB和△COD都是直角三角形,
∴△AOB与△COD全等,
只有AB=OC或AB=OD,
①当AB=OC时,
∵OB=OC,
∴AB=OB=3,
∴∠A=∠AOB=45°,
∵AB=AD,
∴∠ODC=∠ADB=67.5°≠∠AOB,
∴此种情况不存在,
②当AB=OD时,
∵AD=AB,
∴AD=OD,即:OA=2AD=2AB,
在Rt△ABO中,OB=3,
根据勾股定理得,AB2+OB2=AD2,
∴AB2+9=4AB2,
∴AB=
即:存在△AOB与△COD全等,此时AB=.
