四川省江油市八校2020-2021学年九年级上学期12月月考数学试卷(Word版含简单答案)
文档属性
| 名称 | 四川省江油市八校2020-2021学年九年级上学期12月月考数学试卷(Word版含简单答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 478.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-19 00:00:00 | ||
图片预览



文档简介
四川省江油市八校2020-2021学年九年级上学期12月月考数学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
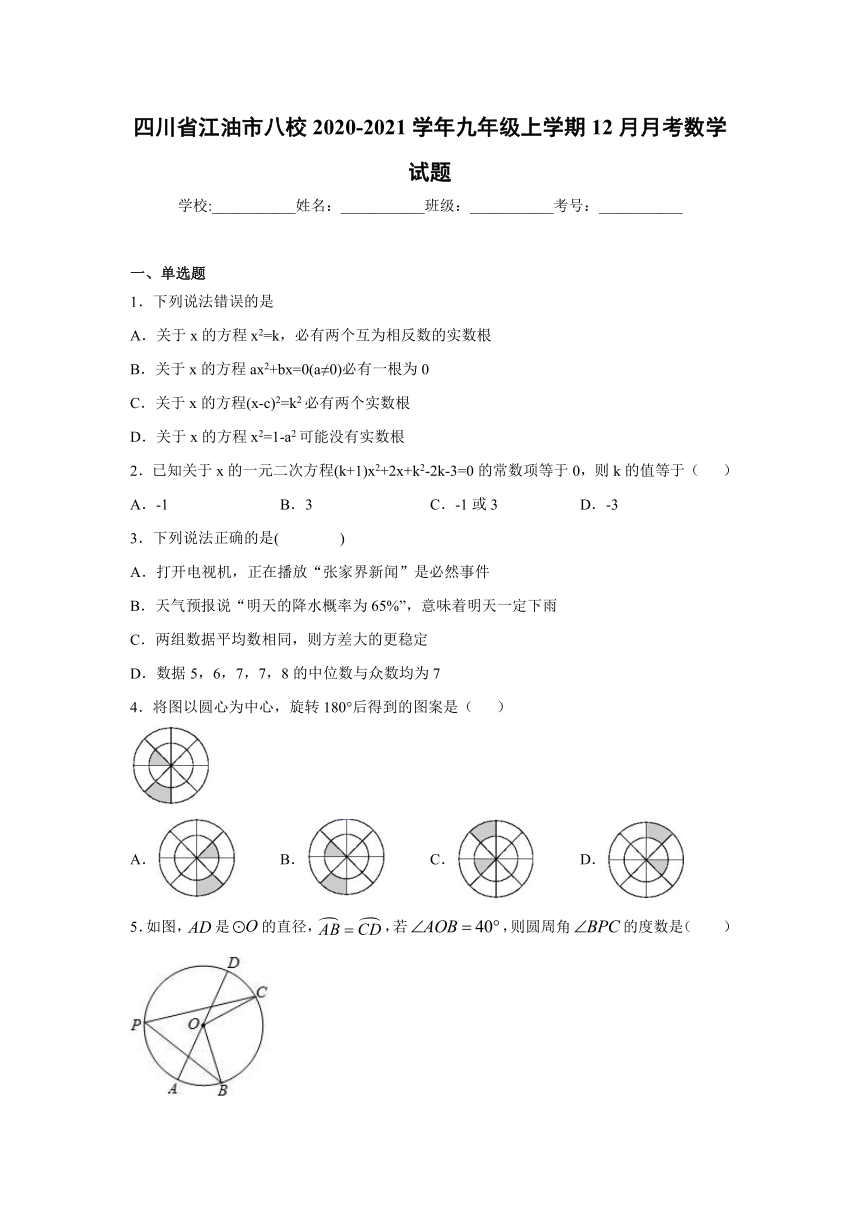
1.下列说法错误的是
A.关于x的方程x2=k,必有两个互为相反数的实数根
B.关于x的方程ax2+bx=0(a≠0)必有一根为0
C.关于x的方程(x-c)2=k2必有两个实数根
D.关于x的方程x2=1-a2可能没有实数根
2.已知关于x的一元二次方程(k+1)x2+2x+k2-2k-3=0的常数项等于0,则k的值等于(
)
A.-1
B.3
C.-1或3
D.-3
3.下列说法正确的是(
)
A.打开电视机,正在播放“张家界新闻”是必然事件
B.天气预报说“明天的降水概率为65%”,意味着明天一定下雨
C.两组数据平均数相同,则方差大的更稳定
D.数据5,6,7,7,8的中位数与众数均为7
4.将图以圆心为中心,旋转180°后得到的图案是(
)
A.
B.
C.
D.
5.如图,是的直径,,若,则圆周角的度数是( )
A.
B.
C.
D.
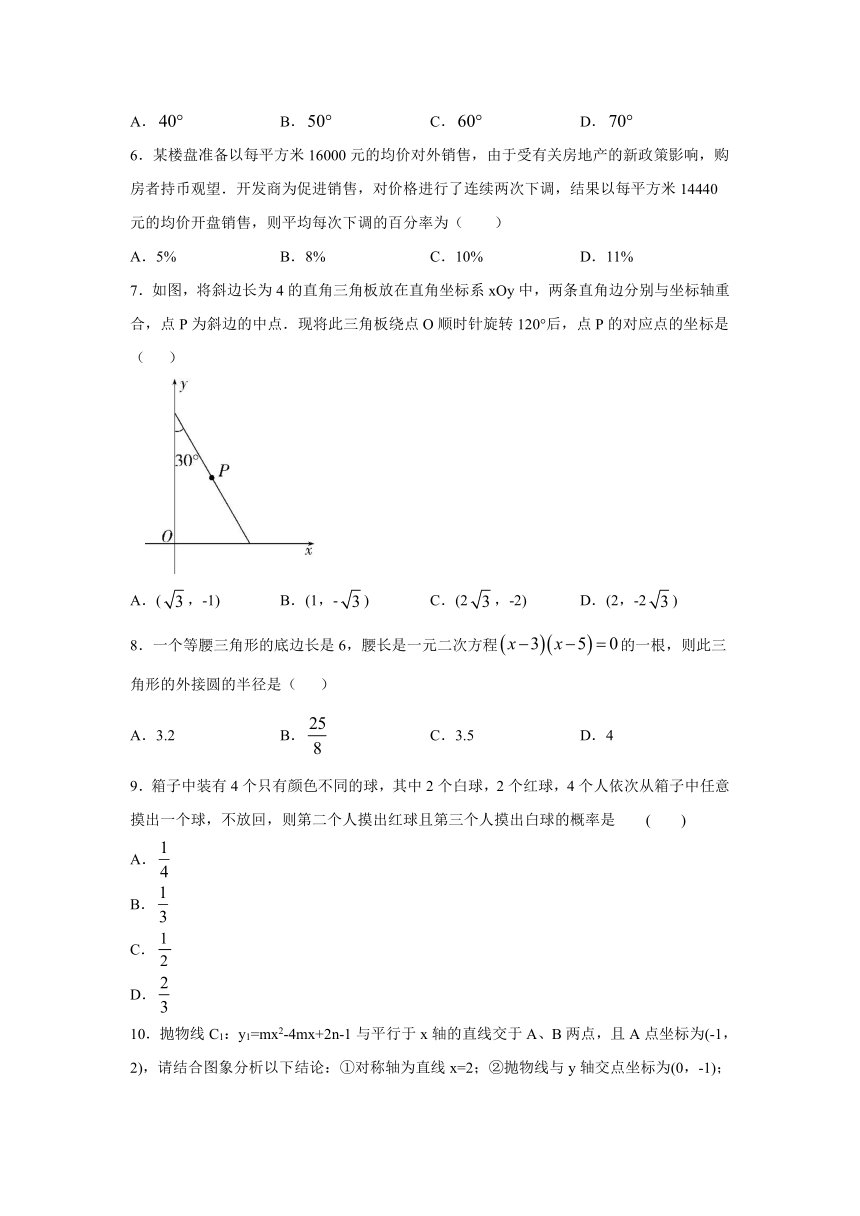
6.某楼盘准备以每平方米16000元的均价对外销售,由于受有关房地产的新政策影响,购房者持币观望.开发商为促进销售,对价格进行了连续两次下调,结果以每平方米14440元的均价开盘销售,则平均每次下调的百分率为( )
A.5%
B.8%
C.10%
D.11%
7.如图,将斜边长为4的直角三角板放在直角坐标系xOy中,两条直角边分别与坐标轴重合,点P为斜边的中点.现将此三角板绕点O顺时针旋转120°后,点P的对应点的坐标是(
)
?
A.(,-1)
B.(1,-)
C.(2,-2)
D.(2,-2)
8.一个等腰三角形的底边长是6,腰长是一元二次方程的一根,则此三角形的外接圆的半径是(
)
A.3.2
B.
C.3.5
D.4
9.箱子中装有4个只有颜色不同的球,其中2个白球,2个红球,4个人依次从箱子中任意摸出一个球,不放回,则第二个人摸出红球且第三个人摸出白球的概率是
(
)
A.
B.
C.
D.
10.抛物线C1:y1=mx2-4mx+2n-1与平行于x轴的直线交于A、B两点,且A点坐标为(-1,2),请结合图象分析以下结论:①对称轴为直线x=2;②抛物线与y轴交点坐标为(0,-1);③m>;④若抛物线C2:y2=ax2(a≠0)与线段AB恰有一个公共点,则a的取值范围是≤a<2;⑤不等式mx2-4mx+2n>0的解作为函数C1的自变量的取值时,对应的函数值均为正数,其中正确结论的个数有(
)
A.2个
B.3个
C.4个
D.5个
二、填空题
11.在一个不透明的袋子中放有a个红球,b个黑球,6个白球,这些球除颜色外完全相同,若每次把球充分搅匀后,任意摸出一个球记下颜色再放回袋子.通过大量重复试验后,发现摸到白球的频率稳定在0.25左右,则a,b的关系是__.
12.有五张背面完全相同的卡片,其正面分别画有等腰三角形,平行四边形,矩形,正方形,菱形,将这五张卡片背面向上洗匀,从中随机抽取一张,卡片上的图形是轴对称图形的概率为___,是中心对称图形的概率为__,既是轴对称图形又是中心对称图形的概率为___.
13.关于x的一元二次方程mx2+nx=0的一根为x=3,则关于x的方程m(x+2)2+nx+2n=0的根为_____.
14.抛物线经过点、两点,则关于的一元二次方程的解是___________
15.为响应“足球进校园”的号召,我县教体局在今年
11
月份组织了“县长杯”校园足球比赛.在某场比赛中,一个球被从地面向上踢出,它距地面的高度
h(m)可用公式
h=﹣5t2+v0t
表示,其中
t(s)表示足球被踢出后经过的时间,v0(m/s)是足球被踢出时的速度,如果足球的最大高度到
20m,那么足球被踢出时的速度应达到________m/s.
16.如图,正方形和,,连接.若绕点旋转,当最大时,_____.
17.如图,正方形ABCD的边长为2a,E为BC边的中点,
的圆心分别在边AB、CD上,这两段圆弧在正方形内交于点F,则E、F间的距离为
.
18.如图,边长为的正方形的顶点、在一个半径为的圆上,顶点、在圆内,将正方形沿圆的内壁逆时针方向作无滑动的滚动.当点第一次落在圆上时,点运动的路径长为________.
19.如图,P是抛物线y=x2﹣4x+3上的一点,以点P为圆心、1个单位长度为半径作⊙P,当⊙P与直线y=0相切时,点P的坐标为_____.
20.抛物线y=x?+2x-3与x轴相交于A、B两点,其顶点为M,将此抛物线在x轴下方的部分沿x轴翻折,其余部分保持不变,得到一个新的图象,如图.在这个新图象上有一点P,能使得S△ABP=6,则点P的坐标为___________.
三、解答题
21.已知关于x的一元二次方程x2+2x+m=0.
(1)当m=3时,判断方程的根的情况;
(2)当m=﹣3时,求方程的根.
22.抛物线中,函数值y与自变量之间的部分对应关系如下表:
…
0
1
…
y
…
0
…
(1)求该抛物线的表达式;
(2)如果将该抛物线平移,使它的顶点移到点M(2,4)的位置,那么其平移的方法是____________.
23.安顺市某商贸公司以每千克40元的价格购进一种干果,计划以每千克60元的价格销售,为了让顾客得到更大的实惠,现决定降价销售,已知这种干果销售量(千克)与每千克降价(元)之间满足一次函数关系,其图象如图所示:
(1)求与之间的函数关系式;
(2)商贸公司要想获利2090元,则这种干果每千克应降价多少元?
24.如图,在中,,,点在的内部,经过,两点,交于点,连接并延长交于点,以,为邻边作.
(1)判断与的位置关系,并说明理由.
(2)若点是的中点,的半径为2,求的长.
25.一个不透明的袋子中装有四个小球,上面分别标有数字-2,-1,0,1,它们除了数字不一样外,其它完全相同.
(1)随机从袋子中摸出一个小球,摸出的球上面标的数字为正数的概率是__________.
(2)小聪先从袋子中随机摸出一个小球,记下数字作为点的纵坐标,如图,已知四边形的四个顶点的坐标分别为,,,,请用画树状图或列表法,求点落在四边形所围成的部分内(含边界)的概率.
26.如图,在平面直角坐标系中,Rt△ABC的斜边AB在y轴上,边AC与x轴交于点D,经过A,D两点的圆的圆心F恰好在y轴上,⊙F与边BC相切于点E,与x轴交于点M,与y轴相交于另一点G,连接AE.
(1)求证:AE平分∠BAC;
(2)若点A,D的坐标分别为(0,﹣1),(2,0),求⊙F的半径;
(3)求经过三点M,F,D的抛物线的解析式.
27.
(1)(操作发现)
如图①,将△ABC绕点A顺时针旋转60°,得到△ADE,连接BD,则∠ABD=____度;
(2)(类比探究)
如图②,在等边三角形ABC内任取一点P,连接PA,PB,PC,求证:以PA,PB,PC的长为三边必能组成三角形:
(3)(解决问题)
如图③,在边长为的等边三角形ABC内有一点P,∠APC=90°,∠BPC=120°,求△APC的面积;
(4)(拓展应用)
图④是A,B,C三个村子位置的平面图,经测量AC=4,BC=5,∠ACB=30°,P为△ABC内的一个动点,连接PA,PB,PC,求PA+PB+PC的最小值.
参考答案
1.A
2.B
3.D
4.D
5.B
6.A
7.B
8.B
9.B
10.A
11.
12.
13.1或﹣2.
14.,.
15.20
16.6
17.a.
18.
19.(2+,1)或(2﹣,1)或(2,﹣1).
20.(-
1+,3)或(-1-,3)或(-2,3)或(0,3)
21.(1)原方程无实数根.
(2)x1=1,x2=﹣3.
22.(1);(2)向右移3个单位,向上移4个单位;
23.(1);(2)商贸公司要想获利2090元,则这种干果每千克应降价9元.
24.(1)是的切线;理由见解析;(2)的长.
25.(1);(2).
26.(1)详见解析;(2)⊙F的半径为;(3)y=﹣x2+.
27.(1)60,理由见解析;(2)见解析;(3)
;(4)
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列说法错误的是
A.关于x的方程x2=k,必有两个互为相反数的实数根
B.关于x的方程ax2+bx=0(a≠0)必有一根为0
C.关于x的方程(x-c)2=k2必有两个实数根
D.关于x的方程x2=1-a2可能没有实数根
2.已知关于x的一元二次方程(k+1)x2+2x+k2-2k-3=0的常数项等于0,则k的值等于(
)
A.-1
B.3
C.-1或3
D.-3
3.下列说法正确的是(
)
A.打开电视机,正在播放“张家界新闻”是必然事件
B.天气预报说“明天的降水概率为65%”,意味着明天一定下雨
C.两组数据平均数相同,则方差大的更稳定
D.数据5,6,7,7,8的中位数与众数均为7
4.将图以圆心为中心,旋转180°后得到的图案是(
)
A.
B.
C.
D.
5.如图,是的直径,,若,则圆周角的度数是( )
A.
B.
C.
D.
6.某楼盘准备以每平方米16000元的均价对外销售,由于受有关房地产的新政策影响,购房者持币观望.开发商为促进销售,对价格进行了连续两次下调,结果以每平方米14440元的均价开盘销售,则平均每次下调的百分率为( )
A.5%
B.8%
C.10%
D.11%
7.如图,将斜边长为4的直角三角板放在直角坐标系xOy中,两条直角边分别与坐标轴重合,点P为斜边的中点.现将此三角板绕点O顺时针旋转120°后,点P的对应点的坐标是(
)
?
A.(,-1)
B.(1,-)
C.(2,-2)
D.(2,-2)
8.一个等腰三角形的底边长是6,腰长是一元二次方程的一根,则此三角形的外接圆的半径是(
)
A.3.2
B.
C.3.5
D.4
9.箱子中装有4个只有颜色不同的球,其中2个白球,2个红球,4个人依次从箱子中任意摸出一个球,不放回,则第二个人摸出红球且第三个人摸出白球的概率是
(
)
A.
B.
C.
D.
10.抛物线C1:y1=mx2-4mx+2n-1与平行于x轴的直线交于A、B两点,且A点坐标为(-1,2),请结合图象分析以下结论:①对称轴为直线x=2;②抛物线与y轴交点坐标为(0,-1);③m>;④若抛物线C2:y2=ax2(a≠0)与线段AB恰有一个公共点,则a的取值范围是≤a<2;⑤不等式mx2-4mx+2n>0的解作为函数C1的自变量的取值时,对应的函数值均为正数,其中正确结论的个数有(
)
A.2个
B.3个
C.4个
D.5个
二、填空题
11.在一个不透明的袋子中放有a个红球,b个黑球,6个白球,这些球除颜色外完全相同,若每次把球充分搅匀后,任意摸出一个球记下颜色再放回袋子.通过大量重复试验后,发现摸到白球的频率稳定在0.25左右,则a,b的关系是__.
12.有五张背面完全相同的卡片,其正面分别画有等腰三角形,平行四边形,矩形,正方形,菱形,将这五张卡片背面向上洗匀,从中随机抽取一张,卡片上的图形是轴对称图形的概率为___,是中心对称图形的概率为__,既是轴对称图形又是中心对称图形的概率为___.
13.关于x的一元二次方程mx2+nx=0的一根为x=3,则关于x的方程m(x+2)2+nx+2n=0的根为_____.
14.抛物线经过点、两点,则关于的一元二次方程的解是___________
15.为响应“足球进校园”的号召,我县教体局在今年
11
月份组织了“县长杯”校园足球比赛.在某场比赛中,一个球被从地面向上踢出,它距地面的高度
h(m)可用公式
h=﹣5t2+v0t
表示,其中
t(s)表示足球被踢出后经过的时间,v0(m/s)是足球被踢出时的速度,如果足球的最大高度到
20m,那么足球被踢出时的速度应达到________m/s.
16.如图,正方形和,,连接.若绕点旋转,当最大时,_____.
17.如图,正方形ABCD的边长为2a,E为BC边的中点,
的圆心分别在边AB、CD上,这两段圆弧在正方形内交于点F,则E、F间的距离为
.
18.如图,边长为的正方形的顶点、在一个半径为的圆上,顶点、在圆内,将正方形沿圆的内壁逆时针方向作无滑动的滚动.当点第一次落在圆上时,点运动的路径长为________.
19.如图,P是抛物线y=x2﹣4x+3上的一点,以点P为圆心、1个单位长度为半径作⊙P,当⊙P与直线y=0相切时,点P的坐标为_____.
20.抛物线y=x?+2x-3与x轴相交于A、B两点,其顶点为M,将此抛物线在x轴下方的部分沿x轴翻折,其余部分保持不变,得到一个新的图象,如图.在这个新图象上有一点P,能使得S△ABP=6,则点P的坐标为___________.
三、解答题
21.已知关于x的一元二次方程x2+2x+m=0.
(1)当m=3时,判断方程的根的情况;
(2)当m=﹣3时,求方程的根.
22.抛物线中,函数值y与自变量之间的部分对应关系如下表:
…
0
1
…
y
…
0
…
(1)求该抛物线的表达式;
(2)如果将该抛物线平移,使它的顶点移到点M(2,4)的位置,那么其平移的方法是____________.
23.安顺市某商贸公司以每千克40元的价格购进一种干果,计划以每千克60元的价格销售,为了让顾客得到更大的实惠,现决定降价销售,已知这种干果销售量(千克)与每千克降价(元)之间满足一次函数关系,其图象如图所示:
(1)求与之间的函数关系式;
(2)商贸公司要想获利2090元,则这种干果每千克应降价多少元?
24.如图,在中,,,点在的内部,经过,两点,交于点,连接并延长交于点,以,为邻边作.
(1)判断与的位置关系,并说明理由.
(2)若点是的中点,的半径为2,求的长.
25.一个不透明的袋子中装有四个小球,上面分别标有数字-2,-1,0,1,它们除了数字不一样外,其它完全相同.
(1)随机从袋子中摸出一个小球,摸出的球上面标的数字为正数的概率是__________.
(2)小聪先从袋子中随机摸出一个小球,记下数字作为点的纵坐标,如图,已知四边形的四个顶点的坐标分别为,,,,请用画树状图或列表法,求点落在四边形所围成的部分内(含边界)的概率.
26.如图,在平面直角坐标系中,Rt△ABC的斜边AB在y轴上,边AC与x轴交于点D,经过A,D两点的圆的圆心F恰好在y轴上,⊙F与边BC相切于点E,与x轴交于点M,与y轴相交于另一点G,连接AE.
(1)求证:AE平分∠BAC;
(2)若点A,D的坐标分别为(0,﹣1),(2,0),求⊙F的半径;
(3)求经过三点M,F,D的抛物线的解析式.
27.
(1)(操作发现)
如图①,将△ABC绕点A顺时针旋转60°,得到△ADE,连接BD,则∠ABD=____度;
(2)(类比探究)
如图②,在等边三角形ABC内任取一点P,连接PA,PB,PC,求证:以PA,PB,PC的长为三边必能组成三角形:
(3)(解决问题)
如图③,在边长为的等边三角形ABC内有一点P,∠APC=90°,∠BPC=120°,求△APC的面积;
(4)(拓展应用)
图④是A,B,C三个村子位置的平面图,经测量AC=4,BC=5,∠ACB=30°,P为△ABC内的一个动点,连接PA,PB,PC,求PA+PB+PC的最小值.
参考答案
1.A
2.B
3.D
4.D
5.B
6.A
7.B
8.B
9.B
10.A
11.
12.
13.1或﹣2.
14.,.
15.20
16.6
17.a.
18.
19.(2+,1)或(2﹣,1)或(2,﹣1).
20.(-
1+,3)或(-1-,3)或(-2,3)或(0,3)
21.(1)原方程无实数根.
(2)x1=1,x2=﹣3.
22.(1);(2)向右移3个单位,向上移4个单位;
23.(1);(2)商贸公司要想获利2090元,则这种干果每千克应降价9元.
24.(1)是的切线;理由见解析;(2)的长.
25.(1);(2).
26.(1)详见解析;(2)⊙F的半径为;(3)y=﹣x2+.
27.(1)60,理由见解析;(2)见解析;(3)
;(4)
同课章节目录
