人教版八年级数学下 19.2.2 第3课时 用待定系数法求一次函数的解析式(共12张)
文档属性
| 名称 | 人教版八年级数学下 19.2.2 第3课时 用待定系数法求一次函数的解析式(共12张) |

|
|
| 格式 | zip | ||
| 文件大小 | 564.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-19 00:00:00 | ||
图片预览





文档简介
(共12张PPT)
第3课时 用待定系数法求一次函数的解析式
一、教学目标
二、教学重难点
重点
难点
1.了解待定系数法的概念.
2.经历用待定系数法求一次函数的解析式的过程,掌握用待定系数法求一次函数解析式的方法,体会方程思想和数形结合的思想.
用待定系数法确定一次函数解析式.
理解k,b的几何意义.
活动1
新课导入
三、教学设计
1.回顾一次函数的概念和性质.
2.直线y=2x-3与x轴的交点坐标为__________,与y轴的交点坐标为___________,图象经过_____________象限,y随x的增大而_______.
3.若已知一次函数图象经过点,
(0,-3),如何求一次函数的解析式?
(0,-3)
一、三、四
增大
活动2
探究新知
思考完成并交流展示.
教材P93例4.
提出问题:
(1)为什么求一次函数解析式,只需要已知两个点的坐标就可以了?
(2)给出两个点的坐标,如何求经过这两个点的直线的解析式?
(3)什么叫做待定系数法?
(4)用待定系数法求一次函数解析式的步骤是什么?
活动3
知识归纳
1.先设出函数的解析式,再根据条件确定解析式中未知数的_______,从而得出函数解析式的方法,叫做_______________.
2.用待定系数法求一次函数解析式的步骤:
(1)设一次函数的解析式为____________;
(2)把满足条件的两个点(x1,y1),(x2,y2)代入解析式中,得到关于k,b的方程组;
(3)解方程组,得到_________的值;
(4)将求出的k,b值回代到所设函数的解析式中,即可得到所求的函数解析式.
以上简记为:“一设、二代、三解、四回代”.
系数
待定系数法
y=kx+b
k,b
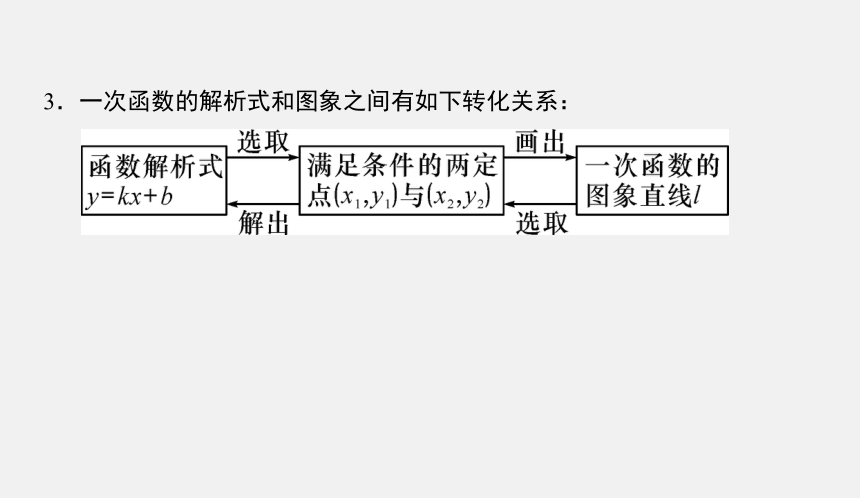
3.一次函数的解析式和图象之间有如下转化关系:
活动4
例题与练习
例1 已知一次函数图象经过点A(3,5)和点B(-4,-9).
(1)求此一次函数的解析式;
(2)若点C(m,2)是该函数图象上一点,求点C的坐标.
解:(1)设此一次函数的解析式为y=kx+b.由题意,
∴此一次函数的解析式为y=2x-1;
(2)∵点C(m,2)在y=2x-1上,
∴2=2m-1,
例2 已知水银体温计的读数y(℃)与水银柱的长度x(cm)之间是一次函数关系.现有一支水银体温计,其部分刻度线不清晰(如图),表中记录的是该体温计部分清晰刻度线及其对应水银柱的长度.
水银柱的长度x(cm)
4.2
…
8.2
9.8
体温计的读数y(℃)
35.0
…
40.0
42.0
(1)求y关于x的函数关系式;(不需要写出函数自变量的取值范围)
(2)用该体温计测体温时,当水银柱的长度为6.2
cm,求此时体温计的读数.
解:(1)设y关于x的函数关系式为y=kx+b.由题意,得
∴y=1.25x+29.75.
∴y关于x的函数关系式为y=1.25x+29.75;
(2)当x=6.2时,y=1.25×6.2+29.75=37.5.
答:此时体温计的读数为37.5
℃.
练
习
1.教材P95练习第1题.
2.已知一次函数y=kx+b的图象与y=x平行,且过点(1,2),那么它必过点(
)
A.(-1,0) B.(2,-1) C.(2,1) D.(0,-1)
3.已知一次函数y=kx+b(k≠0)的图象过点(0,2),且与两坐标轴围成的三角形的面积为2,则此一次函数的解析式为______________________.
A
y=x+2或y=-x+2
练
习
4.如图,一次函数的图象与x轴和y轴分别相交于A,B两点,如果点A的坐标为(2,0),且OA=OB,求这个一次函数的解析式.
解:∵OA=OB,点A的坐标为(2,0),
∴点B的坐标为(0,-2).
设这个一次函数的解析式为y=kx+b.将A,B两点的坐标代入解析式,得
∴这个一次函数的解析式为y=x-2.
五、课堂小结
用待定系数法求一次函数的解析式
2.
根据已知条件列出关于k,b的方程(组);
1.
设所求的一次函数解析式为y=kx+b;
3.
解方程,求出k,b;
4.
把求出的k,b代回解析式即可.
第3课时 用待定系数法求一次函数的解析式
一、教学目标
二、教学重难点
重点
难点
1.了解待定系数法的概念.
2.经历用待定系数法求一次函数的解析式的过程,掌握用待定系数法求一次函数解析式的方法,体会方程思想和数形结合的思想.
用待定系数法确定一次函数解析式.
理解k,b的几何意义.
活动1
新课导入
三、教学设计
1.回顾一次函数的概念和性质.
2.直线y=2x-3与x轴的交点坐标为__________,与y轴的交点坐标为___________,图象经过_____________象限,y随x的增大而_______.
3.若已知一次函数图象经过点,
(0,-3),如何求一次函数的解析式?
(0,-3)
一、三、四
增大
活动2
探究新知
思考完成并交流展示.
教材P93例4.
提出问题:
(1)为什么求一次函数解析式,只需要已知两个点的坐标就可以了?
(2)给出两个点的坐标,如何求经过这两个点的直线的解析式?
(3)什么叫做待定系数法?
(4)用待定系数法求一次函数解析式的步骤是什么?
活动3
知识归纳
1.先设出函数的解析式,再根据条件确定解析式中未知数的_______,从而得出函数解析式的方法,叫做_______________.
2.用待定系数法求一次函数解析式的步骤:
(1)设一次函数的解析式为____________;
(2)把满足条件的两个点(x1,y1),(x2,y2)代入解析式中,得到关于k,b的方程组;
(3)解方程组,得到_________的值;
(4)将求出的k,b值回代到所设函数的解析式中,即可得到所求的函数解析式.
以上简记为:“一设、二代、三解、四回代”.
系数
待定系数法
y=kx+b
k,b
3.一次函数的解析式和图象之间有如下转化关系:
活动4
例题与练习
例1 已知一次函数图象经过点A(3,5)和点B(-4,-9).
(1)求此一次函数的解析式;
(2)若点C(m,2)是该函数图象上一点,求点C的坐标.
解:(1)设此一次函数的解析式为y=kx+b.由题意,
∴此一次函数的解析式为y=2x-1;
(2)∵点C(m,2)在y=2x-1上,
∴2=2m-1,
例2 已知水银体温计的读数y(℃)与水银柱的长度x(cm)之间是一次函数关系.现有一支水银体温计,其部分刻度线不清晰(如图),表中记录的是该体温计部分清晰刻度线及其对应水银柱的长度.
水银柱的长度x(cm)
4.2
…
8.2
9.8
体温计的读数y(℃)
35.0
…
40.0
42.0
(1)求y关于x的函数关系式;(不需要写出函数自变量的取值范围)
(2)用该体温计测体温时,当水银柱的长度为6.2
cm,求此时体温计的读数.
解:(1)设y关于x的函数关系式为y=kx+b.由题意,得
∴y=1.25x+29.75.
∴y关于x的函数关系式为y=1.25x+29.75;
(2)当x=6.2时,y=1.25×6.2+29.75=37.5.
答:此时体温计的读数为37.5
℃.
练
习
1.教材P95练习第1题.
2.已知一次函数y=kx+b的图象与y=x平行,且过点(1,2),那么它必过点(
)
A.(-1,0) B.(2,-1) C.(2,1) D.(0,-1)
3.已知一次函数y=kx+b(k≠0)的图象过点(0,2),且与两坐标轴围成的三角形的面积为2,则此一次函数的解析式为______________________.
A
y=x+2或y=-x+2
练
习
4.如图,一次函数的图象与x轴和y轴分别相交于A,B两点,如果点A的坐标为(2,0),且OA=OB,求这个一次函数的解析式.
解:∵OA=OB,点A的坐标为(2,0),
∴点B的坐标为(0,-2).
设这个一次函数的解析式为y=kx+b.将A,B两点的坐标代入解析式,得
∴这个一次函数的解析式为y=x-2.
五、课堂小结
用待定系数法求一次函数的解析式
2.
根据已知条件列出关于k,b的方程(组);
1.
设所求的一次函数解析式为y=kx+b;
3.
解方程,求出k,b;
4.
把求出的k,b代回解析式即可.
