1.4 角平分线 一课一练（含解析）

初中数学北师大版八年级下学期 第一章 1.4 角平分线
一、单选题
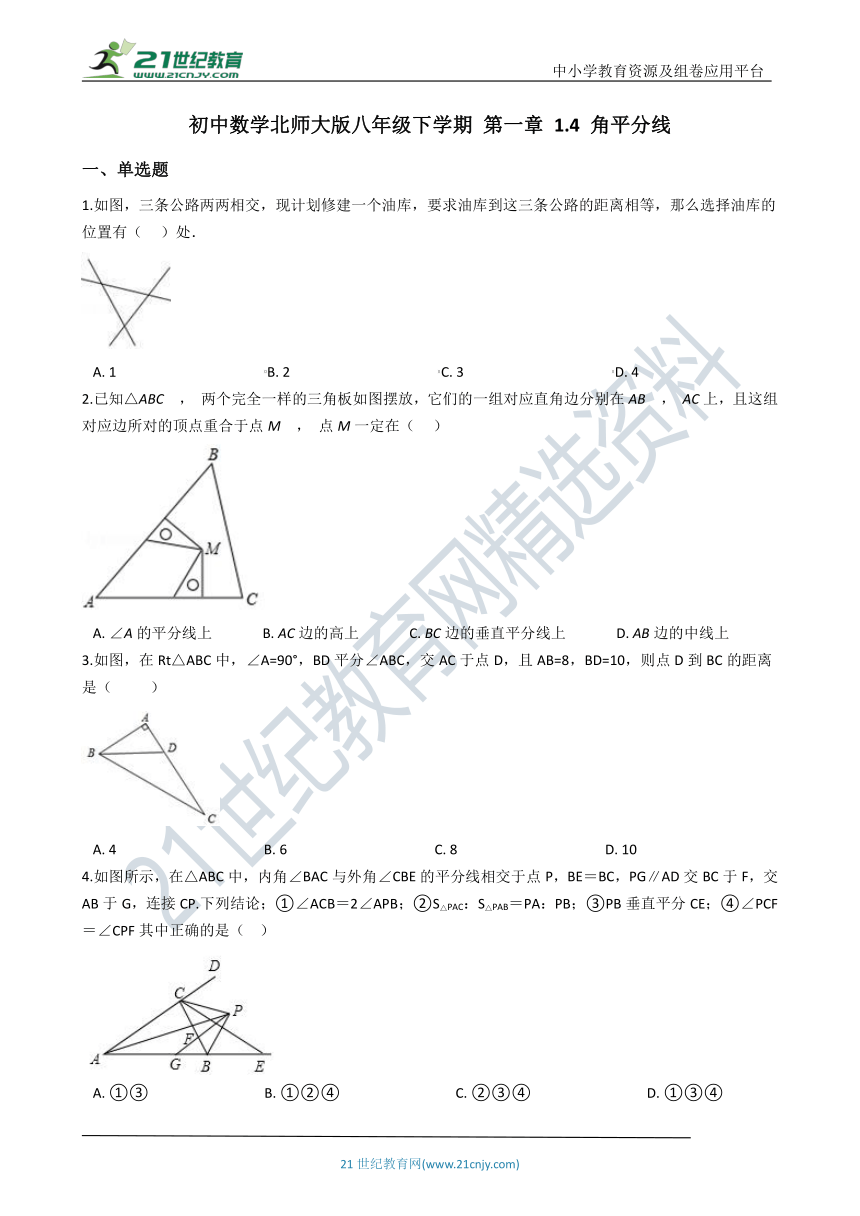
1.如图，三条公路两两相交，现计划修建一个油库，要求油库到这三条公路的距离相等，那么选择油库的位置有（??? ）处．
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
2.已知△ABC ， 两个完全一样的三角板如图摆放，它们的一组对应直角边分别在AB ， AC上，且这组对应边所对的顶点重合于点M ， 点M一定在（??? ）
A.?∠A的平分线上??????????????B.?AC边的高上??????????????C.?BC边的垂直平分线上??????????????D.?AB边的中线上
3.如图，在Rt△ABC中，∠A=90°，BD平分∠ABC，交AC于点D，且AB=8，BD=10，则点D到BC的距离是（ 　　）
A.?4???????????????????????????????????????????B.?6???????????????????????????????????????????C.?8???????????????????????????????????????????D.?10
4.如图所示，在△ABC中，内角∠BAC与外角∠CBE的平分线相交于点P，BE＝BC，PG∥AD交BC于F，交AB于G，连接CP.下列结论；①∠ACB＝2∠APB；②S△PAC：S△PAB＝PA：PB；③PB垂直平分CE；④∠PCF＝∠CPF其中正确的是（?? ）
A.?①③?????????????????????????????????B.?①②④?????????????????????????????????C.?②③④?????????????????????????????????D.?①③④
5.如图，已知∠AOB，以点O为圆心，任意长为半径画弧，交OA于点C，交OB于点D，再分别以C，D为圆心，以大于 CD长为半径画弧，两弧交于点F，作射线OF，点P为OF上一点，PE⊥OB，垂足为点E，若PE＝5，则点P到OA的距离为（?? ）
A.?5??????????????????????????????????????????B.?4??????????????????????????????????????????C.?3??????????????????????????????????????????D.?
6.如图，△ABC中，∠C=90°，AD平分∠BAC，过点D作DE⊥AB于E，测得BC=9，BE=3，则△BDE的周长是（?? ）
A.?15??????????????????????????????????????????B.?12??????????????????????????????????????????C.?9??????????????????????????????????????????D.?6
7.如图，OD平分∠AOB，DE⊥AO于点E，DE=4，点F是射线OB上的任意一点，则DF的长度不可能是（??? ）
A.?3???????????????????????????????????????????B.?4???????????????????????????????????????????C.?5???????????????????????????????????????????D.?6
8.若射线OC在∠AOB内部，则下列①∠AOC=∠BOC；②∠AOB=2∠AOC；③∠AOB=∠AOC+∠BOC；④∠BOC= ∠AOB；能判定射线OC是∠AOB的角平分线的有(??? )
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
二、填空题
9.如图：在Rt△ABC中，∠B＝90°，以顶点C为圆心，适当长为半径画弧，分别交AC、BC于点E、F，再分别以点E、F为圆心，大于EF的长为半径画弧，两弧交于点P，作射线CP交AB于点D，若BD＝2，AC＝6，则△ACD的面积为________．
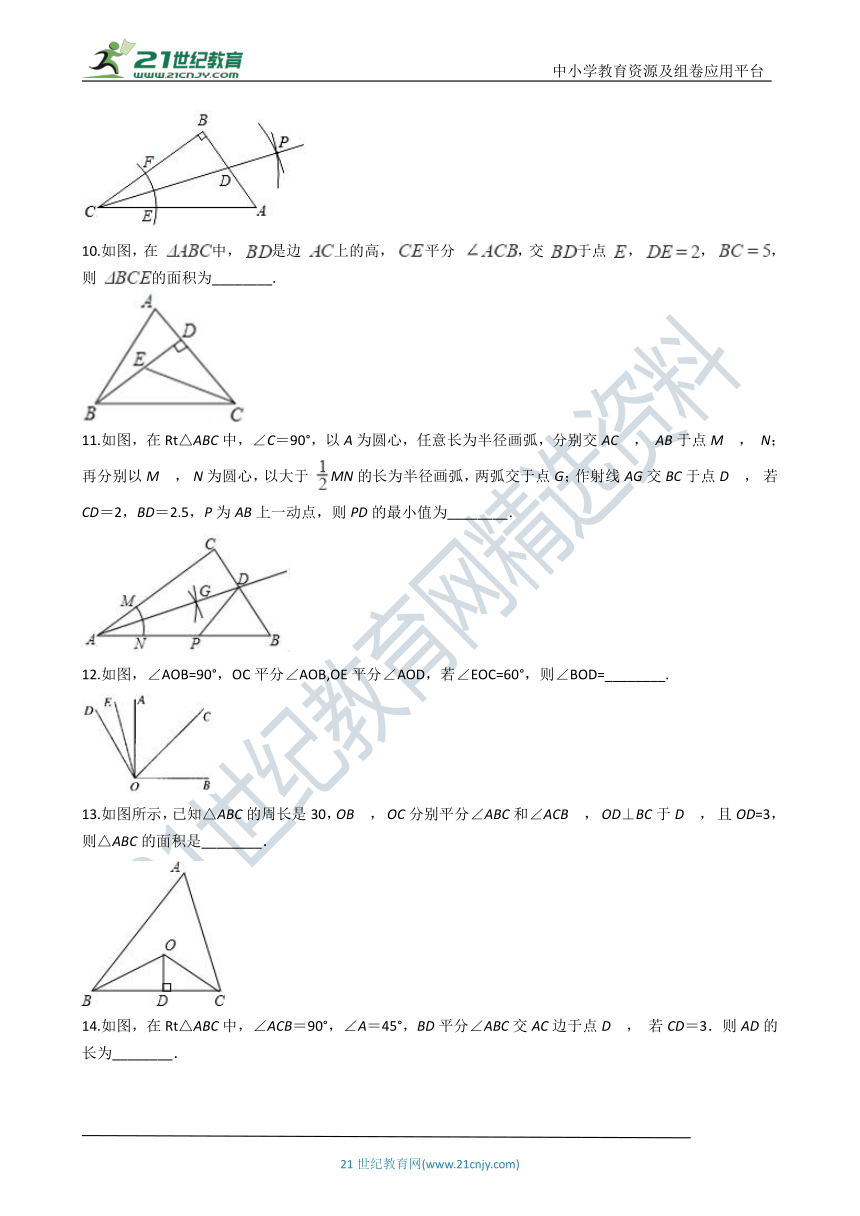
10.如图，在 中， 是边 上的高， 平分 ，交 于点 ， ， ，则 的面积为________.
11.如图，在Rt△ABC中，∠C＝90°，以A为圆心，任意长为半径画弧，分别交AC ， AB于点M ， N；再分别以M ， N为圆心，以大于 MN的长为半径画弧，两弧交于点G；作射线AG交BC于点D ， 若CD＝2，BD＝2.5，P为AB上一动点，则PD的最小值为________．
12.如图，∠AOB=90°，OC平分∠AOB,OE平分∠AOD，若∠EOC=60°，则∠BOD=________.
13.如图所示，已知△ABC的周长是30，OB ， OC分别平分∠ABC和∠ACB ， OD⊥BC于D ， 且OD=3，则△ABC的面积是________．
14.如图，在Rt△ABC中，∠ACB＝90°，∠A＝45°，BD平分∠ABC交AC边于点D ， 若CD＝3．则AD的长为________．
三、解答题
15.如图,在△ABC中,∠C=90°，AB=10，AD是△ABC的一条角平分线。若CD=3，
求 的面积.
16.已知，如图， ， 是 上一点， 、 分别平分 、 .求证： 是 的中点.
答案解析部分
一、单选题
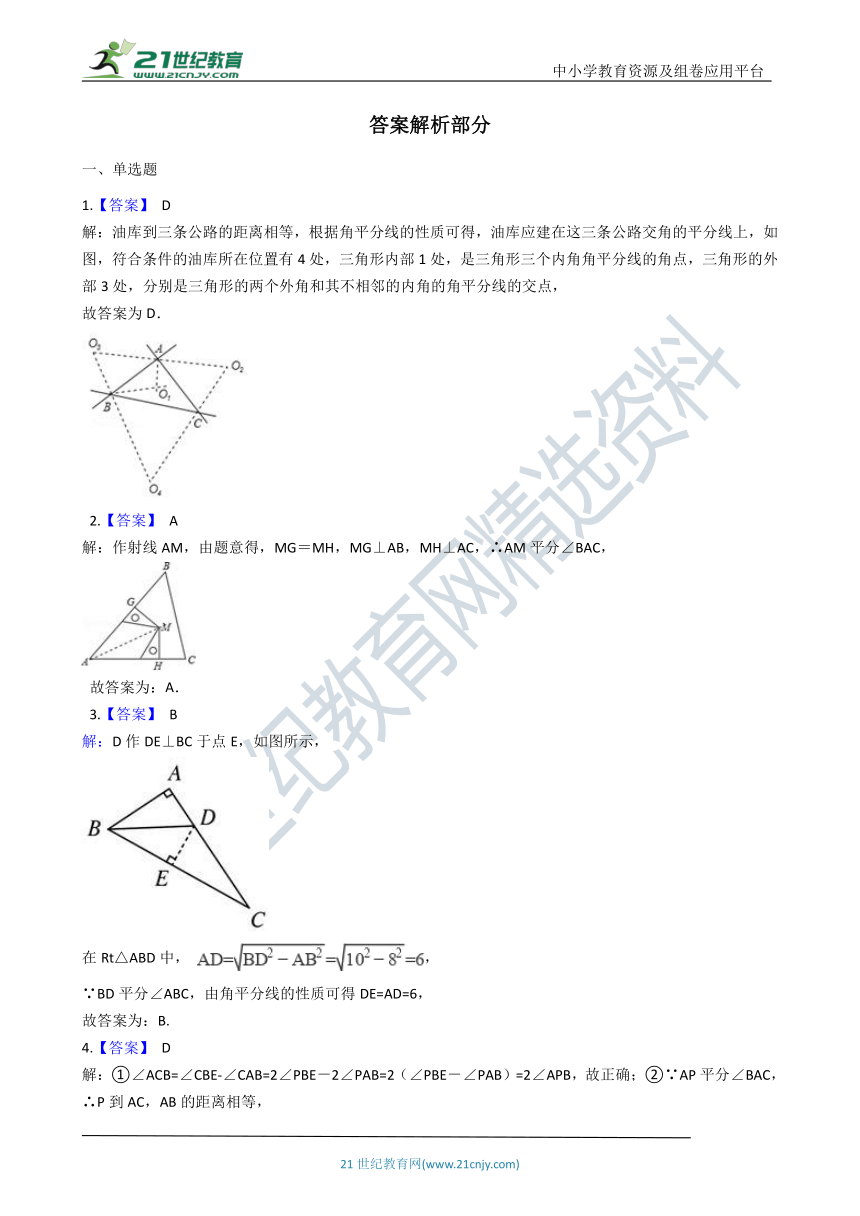
1.【答案】 D
解：油库到三条公路的距离相等，根据角平分线的性质可得，油库应建在这三条公路交角的平分线上，如图，符合条件的油库所在位置有4处，三角形内部1处，是三角形三个内角角平分线的角点，三角形的外部3处，分别是三角形的两个外角和其不相邻的内角的角平分线的交点，
故答案为D．
2.【答案】 A
解：作射线AM，由题意得，MG＝MH，MG⊥AB，MH⊥AC，∴AM平分∠BAC，
故答案为：A．
3.【答案】 B
解：D作DE⊥BC于点E，如图所示，
在Rt△ABD中， ，
∵BD平分∠ABC，由角平分线的性质可得DE=AD=6，
故答案为：B.
4.【答案】 D
解：①∠ACB=∠CBE-∠CAB=2∠PBE－2∠PAB=2（∠PBE－∠PAB）=2∠APB，故正确；②∵AP平分∠BAC，
∴P到AC，AB的距离相等，
∴S△PAC:S△PAB=AC:AB，但不定等于PA：PB，故错误；③∵BE=BC，BP平分∠CBE，
∴PB垂直平分CE(三线合一)，故正确；④∵∠BAC与∠CBE的平分线相交于点P，可得点P也位于∠BCD的平分线上，
∴∠DCP=∠PCF，
又∵PG∥AD，
∴∠CPF=∠DCP，
∴∠PCF＝∠CPF，故正确.
故①③④都正确.
故答案为：D.
5.【答案】 A
解：过点P作PT⊥OA于T.
由作图可知，OF平分∠AOB，
∵PT⊥OA，PE⊥OB，
∴PT＝PE＝5，
故答案为：A.
6.【答案】 B
解：∵△ABC中，∠C=90°
∴AC⊥CD
又∵AD平分∠BAC，DE⊥AB
∴DE=CD
∵BC=9，BE=3
∴△BDE的周长是：BE+BD+DE=BE+BD+CD=BE+BC=3+9=12
故答案为：B
7.【答案】 A
解：∵OD是∠AOB的角平分线，
由“角平分线上的点到角两边的距离相等”可知，
D到OB边的距离等于DE长，即为4，
又由点到直线的距离垂线段最短可知，
DF≥4，
故答案为：A．
8.【答案】 C
解：①∵∠AOC=∠BOC
∴OC平分∠AOB，即OC为∠AOB的角平分线，正确；
②∵∠AOC=∠AOB
∴∠AOB=2∠AOC=∠AOC+∠BOC
∴∠AOC=∠BOC
∴OC平分∠AOB，即OC为∠AOB的平分线。
③∵∠AOC+∠BOC=∠AOB
∴假设∠AOC=30°，∠BOC=40°，，∠AOB=70°，但是OC不是∠AOB的平分线；④∵∠AOB=2∠BOC=∠AOC+∠BOC
∴∠AOC=∠BOC
∴OC平分∠AOB，即OC为∠AOB的角平分线，正确；
故答案为：C.
二、填空题
9.【答案】 6
解：如图，作DQ⊥AC于Q．
由作图知CP是∠ACB的平分线，
∵∠B=90°，BD=2，
∴DB=DQ=2，
∵AC=6，
∴S△ACD AC?DQ ×6×2=6．
故答案为：6．
10.【答案】 5
解：作EF⊥BC于F，
∵CE平分∠ACB，BD⊥AC，EF⊥BC，
∴EF=DE=2，
∴S△BCE= BC?EF= ×5×2=5.
故答案为：5.
11.【答案】 2
解：由作法得AD平分∠BAC ，
∴点D到AB的距离等于DC＝2，
∴PD的最小值为2．
故答案为：2．
12.【答案】 120?
解：∵∠AOB=90°，OC平分∠AOB，
∴∠AOC= ∠AOB= ×90°=45°，
∵∠EOC=60°，
∴∠AOE=∠EOC-∠AOC=60°-45°=15°，
∵OE平分∠AOD，
∴∠AOD=2∠AOE=2×15°=30°．
∴∠BOD=30°+90°=120°.
即答案为120°.
13.【答案】 45
解：如图，连接OA，过O作OE⊥AB于E，OF⊥AC于F，
∵OB、OC分别平分∠ABC和∠ACB，
∴OE＝OF＝OD＝3，
∵△ABC的周长是30，OD⊥BC于D，且OD＝3，
∴S△ABC＝ ×AB×OE＋ ×BC×OD＋ ×AC×OF＝ ×（AB＋BC＋AC）×3
＝ ×30×3＝45，
故答案为：45．
【分析】根据角平分线上的点到角的两边的距离相等可得点O到AB、AC、BC的距离都相等（即OE＝OD＝OF），从而可得到△ABC的面积等于周长的一半乘以3，代入求出即可．
14.【答案】
解：如图，过D作DG⊥AB于G，
∵BD平分∠ABC，∠ACB＝90°，
∴CD＝DG＝3，
∵∠A＝45°，∠AGD＝90°，
∴AG＝DG＝3，
∴AD＝ ，
故答案为： ．
三、解答题
15.【答案】 解：作DE⊥AB于E.
∵AD平分∠BAC，DE⊥AB，DC⊥AC，
∴DE=CD=3.
∴△ABD的面积为 ×3×10=15.
16.【答案】 解：过点 作 于点
∵
∴ ?????????
又∵ ????????? 平分
∴
∵ ????????? 平分
∴
∴
∴ 是 的中点