1.3 线段的垂直平分线 一课一练(含解析)
文档属性
| 名称 | 1.3 线段的垂直平分线 一课一练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-19 21:11:01 | ||
图片预览




文档简介
初中数学北师大版八年级下学期 第一章 1.3 线段的垂直平分线
一、单选题
1.如图,DE是△ABC的边AB的垂直平分线,D为垂足,DE交AC于点E,且AC=8,BC=5,则△BEC的周长是(?? )
A.?12?????????????????????????????????????????B.?13?????????????????????????????????????????C.?14?????????????????????????????????????????D.?15
2.如图,已知 ,以 两点为圆心,大于 的长为半径画圆,两弧相交于点 ,连接 与 相较于点 ,则 的周长为(??? )
A.?8?????????????????????????????????????????B.?10?????????????????????????????????????????C.?11?????????????????????????????????????????D.?13
3.如图,在△ABC中,∠C=90°,AD平分∠BAC,且DE⊥AB于E,DE=5,BC=11,则BD的长为(??? )
A.?5???????????????????????????????????????????B.?6???????????????????????????????????????????C.?7???????????????????????????????????????????D.?8
4.如图,AC=AD,BC=BD,则有( )
A.?AB垂直平分CD????????????B.?CD垂直平分AB????????????C.?AB与CD互相垂直平分????????????D.?CD平分∠ACB
5.如图,DE是△ABC中AC边的垂直平分线,若BC=8,AB=10,则△EBC的周长为(?? ).
A.?16?????????????????????????????????????????B.?18?????????????????????????????????????????C.?26?????????????????????????????????????????D.?28
6.如图,在△ABE中,AE的垂直平分线MN交BE于点C,∠E=30°,且AB=CE,则∠BAE的度数是(?????? )
A.?80°??????????????????????????????????????B.?85°??????????????????????????????????????C.?90°??????????????????????????????????????D.?105°
7.若一个三角形两边的垂直平分线的交点在第三边上,则这个三角形是( )
A.?锐角三角形????????????????????????B.?钝角三角形????????????????????????C.?直角三角形????????????????????????D.?不能确定
8.如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中正确结论的个数是( )
A.?4个???????????????????????????????????????B.?3个???????????????????????????????????????C.?2个???????????????????????????????????????D.?1个
二、填空题
9.已知点O为△ABC三边垂直平分线的交点,点O到顶点A的距离为6cm,则OA+OB+OC=________.
10.在△ABC中,边AB、BC、AC的垂直平分线相交于P,则PA、PB、PC的大小关系是________.
11.如图,在△ABC中,已知AC=27,AB的垂直平分线交AB于点D,交AC与点E,若三角形BCE的周长等于50,则BC的长为________.
12.如图所示,在△ABC中,∠BAC=106°,EF、MN分别是AB、AC的垂直平分线,点E、N在BC上,则∠EAN=________.
13.如图,在菱形 中, ,取大于 的长为半径,分别以点 , 为圆心作弧相交于两点,过此两点的直线交 边于点 (作图痕迹如图所示),连接 , ,则 的度数为________.
三、解答题
14.已知,如图,在△ABC中,边AC的垂直平分线DE交AC于E,交BC于D,若AE=3cm,△ABD的周长为13cm,求△ABC的周长.
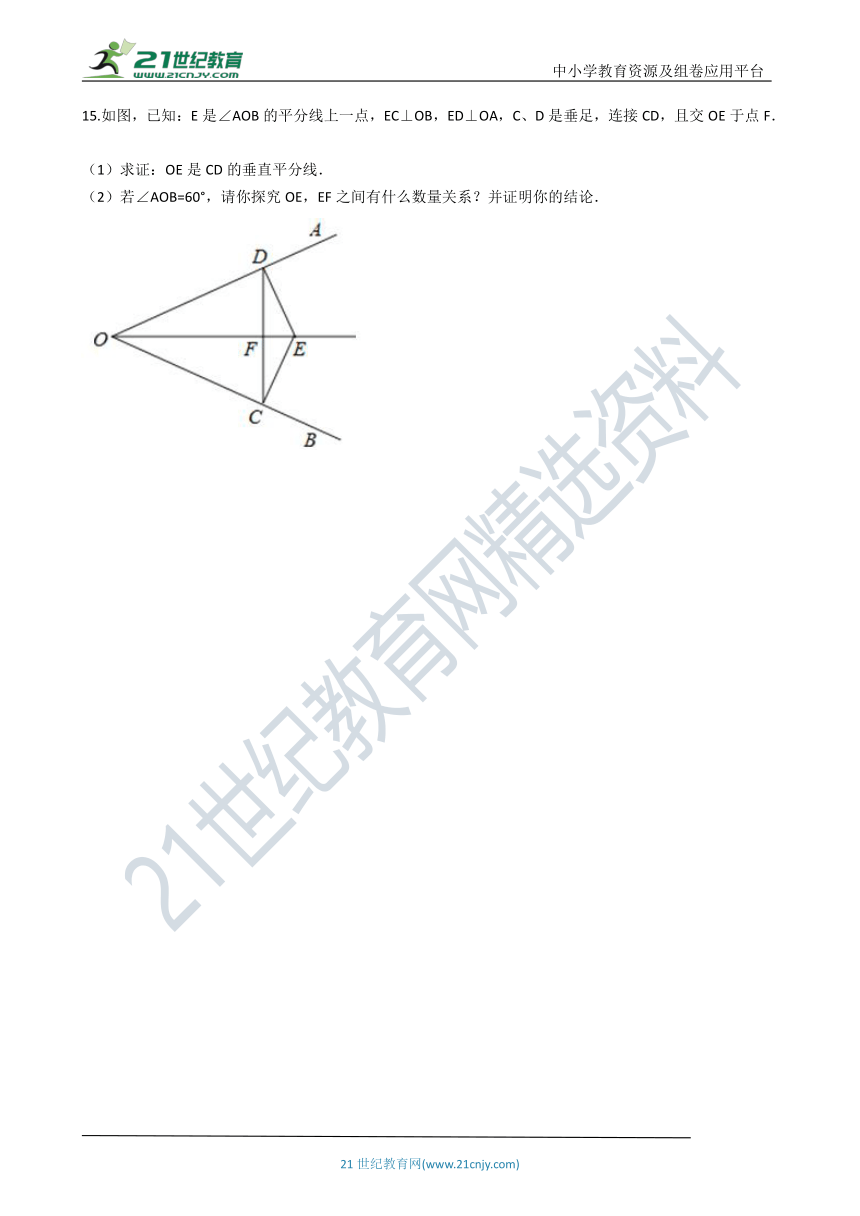
15.如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,且交OE于点F.
(1)求证:OE是CD的垂直平分线.
(2)若∠AOB=60°,请你探究OE,EF之间有什么数量关系?并证明你的结论.
答案解析部分
一、单选题
1.【答案】 B
解:∵DE是△ABC的边AB的垂直平分线,
∴AE=BE,
∵AC=8,BC=5,
∴△BEC的周长是:BE+EC+BC=AE+EC+BC=AC+BC=13。
故答案为:B。
2.【答案】 A
解:由作法得MN垂直平分AB,
∴DA=DB,
∴△BDC的周长=DB+DC+BC=DA+DC+BC=AC+BC=5+3=8.
故答案为:A.
3.【答案】 B
解:∵∠C=90°,AD平分∠BAC,DE⊥AB于E,
∴CD=DE=5,
∵BC=11,
∴BD=6.
故答案为:B.
4.【答案】 A
解:∵AC=AD,BC=BD,∴点A,B在线段CD的垂直平分线上,∴AB垂直平分CD.故选A.
5.【答案】 B
解:∵DE是△ABC中AC边的垂直平分线,
∴AE=CE,
∴AE+BE=CE+BE=10,
∴△EBC的周长=BC+BE+CE=10+8=18,
故答案为:B
6.【答案】 C
解:∵点C在AE的垂直平分线MN上
∴AC=CE
∴∠EAC=∠E=30°
又∵AB=CE
∴AB=AC
∴∠B=∠ACB
又∵∠ACB是△ACE的外角
∴∠ACB=∠EAC+∠E=60°
∴∠B=∠ACB=60°
在△ABE中,∠BAE+∠E+∠B=180°
∴∠BAE=180°-∠E-∠B=180°-30°-60°=90°。
故答案为:C.
7.【答案】 C
解:如图,CA、CB的中点分别为D、E,CA、CB的垂直平分线OD、OE相交于点O,且点O落在AB边上, 连接CO,
∵OD是AC的垂直平分线,
∴OC=OA,
同理OC=OB,
∴OA=OB=OC,
∴A、B、C都落在以O为圆心,以AB为直径的圆周上,
∴∠C是直角。
故选C.
8.【答案】 B
解:①∵矩形ABCD中,O为AC中点,
∴OB=OC,
∵∠COB=60°,
∴△OBC是等边三角形,
∴OB=BC,
∵FO=FC,
∴FB垂直平分OC,
故①正确;
②∵FB垂直平分OC,
∴△CMB≌△OMB,
∵OA=OC,∠FOC=∠EOA,∠DCO=∠BAO,
∴△FOC≌△EOA,
∴FO=EO,
易得OB⊥EF,
∴△OMB≌△OEB,
∴△EOB≌△CMB,
故②正确;
③由△OMB≌△OEB≌△CMB得∠1=∠2=∠3=30°,BF=BE,
∴△BEF是等边三角形,
∴BF=EF,
∵DF∥BE且DF=BE,
∴四边形DEBF是平行四边形,
∴DE=BF,
∴DE=EF,
故③正确;
④在直角△BOE中∵∠3=30°,
∴BE=2OE,
∵∠OAE=∠AOE=30°,
∴AE=OE,
∴BE=2AE,
∴S△AOE:S△BCM=S△AOE:S△BOE=1:2,
故④错误;
所以其中正确结论的个数为3个;
故选B
二、填空题
9.【答案】 18cm
解:∵点O是△ABC三边垂直平分线的交点,
∴OB=OC=OA=6cm,
∴OA+OB+OC=18cm.
故答案为:18cm.
10.【答案】 PA=PB=PC
解:∵边AB的垂直平分线相交于P,
∴PA=PB,
∵边BC的垂直平分线相交于P,
∴PB=PC,
∴PA=PB=PC.
故答案为:PA=PB=PC.
11.【答案】 23
解:∵DE是线段AB的垂直平分线,
∴AE=BE,
∴△BCE的周长=BE+CE+BC=AE+CE+BC=AC+BC,
∴BC=50-27=23.
故答案为:23.
12.【答案】 32°
解:∵△ABC中,∠BAC=106°,
∴∠B+∠C=180°﹣∠BAC=180°﹣106°=74°,
∵EF、MN分别是AB、AC的中垂线,
∴∠B=∠BAE,∠C=∠CAN,
即∠B+∠C=∠BAE+∠CAN=74°,
∴∠EAN=∠BAC﹣(∠BAE+∠CAN)=106°﹣74°=32°.
故答案为32°
13.【答案】 45°
解:
∵
∴
∴
故答案为:45°.
三、解答题
14.【答案】 解:∵DE是边AC的垂直平分线,
∴AD=CD,AE=EC,
∵AE=3cm,△ABD的周长为13cm,
∴AC=AE+EC=3+3=6cm,
△ABD的周长=AB+AD+BD=AB+CD+BD=AB+BC=13cm,
所以,△ABC的周长=AB+BC+AC=13+6=19cm.
15.【答案】 解:(1)∵E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,
∴DE=CE,OE=OE,
∴Rt△ODE≌Rt△OCE,
∴OD=OC,
∴△DOC是等腰三角形,
∵OE是∠AOB的平分线,
∴OE是CD的垂直平分线;
(2)∵OE是∠AOB的平分线,∠AOB=60°,
∴∠AOE=∠BOE=30°,
∵EC⊥OB,ED⊥OA,
∴OE=2DE,∠ODF=∠OED=60°,
∴∠EDF=30°,
∴DE=2EF,
∴OE=4EF.
一、单选题
1.如图,DE是△ABC的边AB的垂直平分线,D为垂足,DE交AC于点E,且AC=8,BC=5,则△BEC的周长是(?? )
A.?12?????????????????????????????????????????B.?13?????????????????????????????????????????C.?14?????????????????????????????????????????D.?15
2.如图,已知 ,以 两点为圆心,大于 的长为半径画圆,两弧相交于点 ,连接 与 相较于点 ,则 的周长为(??? )
A.?8?????????????????????????????????????????B.?10?????????????????????????????????????????C.?11?????????????????????????????????????????D.?13
3.如图,在△ABC中,∠C=90°,AD平分∠BAC,且DE⊥AB于E,DE=5,BC=11,则BD的长为(??? )
A.?5???????????????????????????????????????????B.?6???????????????????????????????????????????C.?7???????????????????????????????????????????D.?8
4.如图,AC=AD,BC=BD,则有( )
A.?AB垂直平分CD????????????B.?CD垂直平分AB????????????C.?AB与CD互相垂直平分????????????D.?CD平分∠ACB
5.如图,DE是△ABC中AC边的垂直平分线,若BC=8,AB=10,则△EBC的周长为(?? ).
A.?16?????????????????????????????????????????B.?18?????????????????????????????????????????C.?26?????????????????????????????????????????D.?28
6.如图,在△ABE中,AE的垂直平分线MN交BE于点C,∠E=30°,且AB=CE,则∠BAE的度数是(?????? )
A.?80°??????????????????????????????????????B.?85°??????????????????????????????????????C.?90°??????????????????????????????????????D.?105°
7.若一个三角形两边的垂直平分线的交点在第三边上,则这个三角形是( )
A.?锐角三角形????????????????????????B.?钝角三角形????????????????????????C.?直角三角形????????????????????????D.?不能确定
8.如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中正确结论的个数是( )
A.?4个???????????????????????????????????????B.?3个???????????????????????????????????????C.?2个???????????????????????????????????????D.?1个
二、填空题
9.已知点O为△ABC三边垂直平分线的交点,点O到顶点A的距离为6cm,则OA+OB+OC=________.
10.在△ABC中,边AB、BC、AC的垂直平分线相交于P,则PA、PB、PC的大小关系是________.
11.如图,在△ABC中,已知AC=27,AB的垂直平分线交AB于点D,交AC与点E,若三角形BCE的周长等于50,则BC的长为________.
12.如图所示,在△ABC中,∠BAC=106°,EF、MN分别是AB、AC的垂直平分线,点E、N在BC上,则∠EAN=________.
13.如图,在菱形 中, ,取大于 的长为半径,分别以点 , 为圆心作弧相交于两点,过此两点的直线交 边于点 (作图痕迹如图所示),连接 , ,则 的度数为________.
三、解答题
14.已知,如图,在△ABC中,边AC的垂直平分线DE交AC于E,交BC于D,若AE=3cm,△ABD的周长为13cm,求△ABC的周长.
15.如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,且交OE于点F.
(1)求证:OE是CD的垂直平分线.
(2)若∠AOB=60°,请你探究OE,EF之间有什么数量关系?并证明你的结论.
答案解析部分
一、单选题
1.【答案】 B
解:∵DE是△ABC的边AB的垂直平分线,
∴AE=BE,
∵AC=8,BC=5,
∴△BEC的周长是:BE+EC+BC=AE+EC+BC=AC+BC=13。
故答案为:B。
2.【答案】 A
解:由作法得MN垂直平分AB,
∴DA=DB,
∴△BDC的周长=DB+DC+BC=DA+DC+BC=AC+BC=5+3=8.
故答案为:A.
3.【答案】 B
解:∵∠C=90°,AD平分∠BAC,DE⊥AB于E,
∴CD=DE=5,
∵BC=11,
∴BD=6.
故答案为:B.
4.【答案】 A
解:∵AC=AD,BC=BD,∴点A,B在线段CD的垂直平分线上,∴AB垂直平分CD.故选A.
5.【答案】 B
解:∵DE是△ABC中AC边的垂直平分线,
∴AE=CE,
∴AE+BE=CE+BE=10,
∴△EBC的周长=BC+BE+CE=10+8=18,
故答案为:B
6.【答案】 C
解:∵点C在AE的垂直平分线MN上
∴AC=CE
∴∠EAC=∠E=30°
又∵AB=CE
∴AB=AC
∴∠B=∠ACB
又∵∠ACB是△ACE的外角
∴∠ACB=∠EAC+∠E=60°
∴∠B=∠ACB=60°
在△ABE中,∠BAE+∠E+∠B=180°
∴∠BAE=180°-∠E-∠B=180°-30°-60°=90°。
故答案为:C.
7.【答案】 C
解:如图,CA、CB的中点分别为D、E,CA、CB的垂直平分线OD、OE相交于点O,且点O落在AB边上, 连接CO,
∵OD是AC的垂直平分线,
∴OC=OA,
同理OC=OB,
∴OA=OB=OC,
∴A、B、C都落在以O为圆心,以AB为直径的圆周上,
∴∠C是直角。
故选C.
8.【答案】 B
解:①∵矩形ABCD中,O为AC中点,
∴OB=OC,
∵∠COB=60°,
∴△OBC是等边三角形,
∴OB=BC,
∵FO=FC,
∴FB垂直平分OC,
故①正确;
②∵FB垂直平分OC,
∴△CMB≌△OMB,
∵OA=OC,∠FOC=∠EOA,∠DCO=∠BAO,
∴△FOC≌△EOA,
∴FO=EO,
易得OB⊥EF,
∴△OMB≌△OEB,
∴△EOB≌△CMB,
故②正确;
③由△OMB≌△OEB≌△CMB得∠1=∠2=∠3=30°,BF=BE,
∴△BEF是等边三角形,
∴BF=EF,
∵DF∥BE且DF=BE,
∴四边形DEBF是平行四边形,
∴DE=BF,
∴DE=EF,
故③正确;
④在直角△BOE中∵∠3=30°,
∴BE=2OE,
∵∠OAE=∠AOE=30°,
∴AE=OE,
∴BE=2AE,
∴S△AOE:S△BCM=S△AOE:S△BOE=1:2,
故④错误;
所以其中正确结论的个数为3个;
故选B
二、填空题
9.【答案】 18cm
解:∵点O是△ABC三边垂直平分线的交点,
∴OB=OC=OA=6cm,
∴OA+OB+OC=18cm.
故答案为:18cm.
10.【答案】 PA=PB=PC
解:∵边AB的垂直平分线相交于P,
∴PA=PB,
∵边BC的垂直平分线相交于P,
∴PB=PC,
∴PA=PB=PC.
故答案为:PA=PB=PC.
11.【答案】 23
解:∵DE是线段AB的垂直平分线,
∴AE=BE,
∴△BCE的周长=BE+CE+BC=AE+CE+BC=AC+BC,
∴BC=50-27=23.
故答案为:23.
12.【答案】 32°
解:∵△ABC中,∠BAC=106°,
∴∠B+∠C=180°﹣∠BAC=180°﹣106°=74°,
∵EF、MN分别是AB、AC的中垂线,
∴∠B=∠BAE,∠C=∠CAN,
即∠B+∠C=∠BAE+∠CAN=74°,
∴∠EAN=∠BAC﹣(∠BAE+∠CAN)=106°﹣74°=32°.
故答案为32°
13.【答案】 45°
解:
∵
∴
∴
故答案为:45°.
三、解答题
14.【答案】 解:∵DE是边AC的垂直平分线,
∴AD=CD,AE=EC,
∵AE=3cm,△ABD的周长为13cm,
∴AC=AE+EC=3+3=6cm,
△ABD的周长=AB+AD+BD=AB+CD+BD=AB+BC=13cm,
所以,△ABC的周长=AB+BC+AC=13+6=19cm.
15.【答案】 解:(1)∵E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,
∴DE=CE,OE=OE,
∴Rt△ODE≌Rt△OCE,
∴OD=OC,
∴△DOC是等腰三角形,
∵OE是∠AOB的平分线,
∴OE是CD的垂直平分线;
(2)∵OE是∠AOB的平分线,∠AOB=60°,
∴∠AOE=∠BOE=30°,
∵EC⊥OB,ED⊥OA,
∴OE=2DE,∠ODF=∠OED=60°,
∴∠EDF=30°,
∴DE=2EF,
∴OE=4EF.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
