1.1 等腰三角形 一课一练(含解析)
文档属性
| 名称 | 1.1 等腰三角形 一课一练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-19 00:00:00 | ||
图片预览




文档简介
初中数学北师大版八年级下学期 第一章 1.1 等腰三角形
一、单选题
1.在等腰三角形ABC中,它的两边长分别为8cm和4cm,则它的周长为( ??)
A.?10cm?????????????????????????????B.?12 cm?????????????????????????????C.?20 cm或16 cm?????????????????????????????D.?20 cm
2.如果等腰三角形的一个外角为140°,那么底角为(?? )
A.?40°????????????????????????????????????B.?60°????????????????????????????????????C.?70°????????????????????????????????????D.?40°或70°
3.下列说法正确的是(?? )
A.?等腰三角形的角平分线、中线和高三线重合????????B.?等角对等边
C.?等腰三角形一定是锐角三角形?????????????????????????????D.?等腰三角形两个底角相等
4.已知 是 的两边,且 ,则 的形状是(? )
A.?等腰三角形?????????????????????????B.?等边三角形?????????????????????????C.?锐角三角形?????????????????????????D.?不确定
5.如图,在平面直角坐标系中,点A的坐标为 ,在x轴上确定点P,使 为等腰三角形,则符合条件的点P有(? )
A.?2个???????????????????????????????????????B.?3个???????????????????????????????????????C.?4个???????????????????????????????????????D.?5个
6.如图,在△ABC中,BF、CF分别平分∠ABC和∠ACB , 过点F作EG∥BC分别交于点AB、AC于点E、G . 若AB=9,BC=10,AC=11,则△AEG的周长为( )
A.?15?????????????????????????????????????????B.?20?????????????????????????????????????????C.?21?????????????????????????????????????????D.?19
7.等腰三角形一腰上的高与底边所夹的角( )
A.?等于顶角?????????????????B.?等于顶角的一半?????????????????C.?等于顶角的2倍?????????????????D.?等于底角的一半
8.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC 交AB于点E,交AC于点F,过点O作OD⊥AC于点D,下列四个结论:①EF=BE+CF; ②∠BOC=90°+ ∠A;③点O到△ABC各边的距离相等;④设OD=m,AE+AF=n,则S△AEF=mn.
其中正确的结论是(???? )
A.?①②③????????????????????????????????B.?①②④????????????????????????????????C.?②③④????????????????????????????????D.?①③④
二、填空题
9.如图,△ABC的周长为18,且AB=AC,AD⊥BC于D,△ACD的周长为13,那么AD的长为________.
10.在△ABC 中,AB=AC,AD⊥BC,BC=10cm, 则 BD=________ cm.
11.如图,△ABC中.点D在BC边上,BD=AD=AC,E为CD的中点.若∠CAE=16°,则∠B为________度.
12.如图,已知点P是射线 上一动点, 若 为等腰三角形,则 ________.
13.如图,矩形ABCD中,AB=10,BC=4,Q为AB边的中点,P为CD边上的动点,且△AQP是腰长为5的等腰三角形,则CP的长为________.
三、解答题
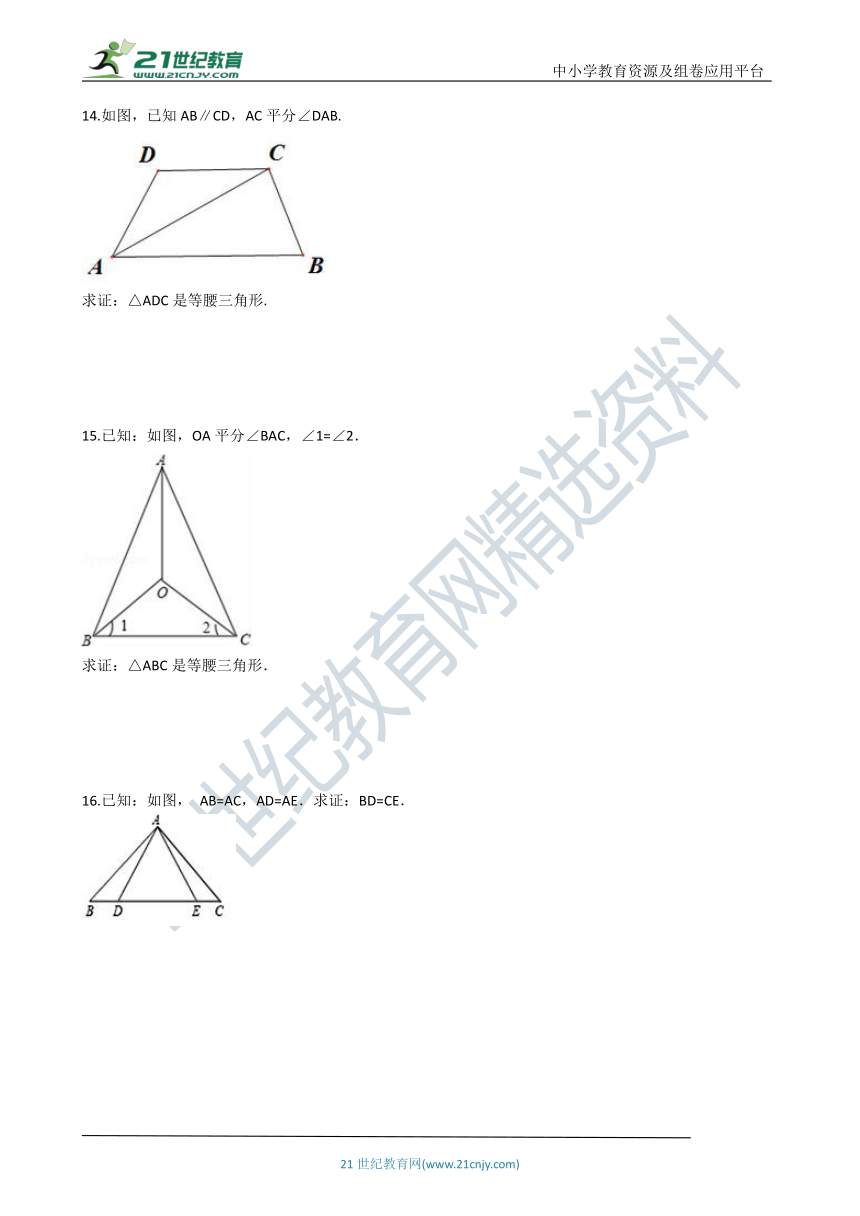
14.如图,已知AB∥CD,AC平分∠DAB.
求证:△ADC是等腰三角形.
15.已知:如图,OA平分∠BAC,∠1=∠2.
求证:△ABC是等腰三角形.
16.已知:如图, AB=AC,AD=AE.求证:BD=CE.
答案解析部分
一、单选题
1.【答案】 D
解:①当腰是4,底边是8时,4+4=8,不满足三角形的三边关系,因此舍去.
②当底边是4,腰长是8时,能构成三角形,则其周长=8+8+4=20.
故答案为:D.
2.【答案】 D
解:∵外角为140°,∴与它相邻的内角是180°﹣140°=40°;
①当40°是顶角时,底角是(180°﹣40°)÷2=70°;②当40°是底角时,底角是40°.
故答案为:D.
3.【答案】 D
解: A:等腰三角形的顶角平分线、底边上的中线和高三线重合,不符合题意;
B、?在同一三角形中等角对等边,不符合题意;
C、 等腰三角形不一定是锐角三角形,如顶角是120°,底角为30°的等腰三角形,不符合题意;
D、 等腰三角形两个底角相等,正确,符合题意;
故答案为:D.
4.【答案】 A
解:因为: ,所以: ,
所以: ,所以三角形ABC是等腰三角形,
故答案为:A.
5.【答案】 C
解:如图,
,
当AO=OP1 , AO=OP3时,P1(﹣ ,0),P3( ,0),
当AP2=OP2时,P2(1,0),
当AO=AP4时,P4(2,0),
故符合条件的点有4个.
故答案为:C.
6.【答案】 B
解:∵EG∥BC ,
∴∠EFB=∠FBC , ∠GFC=∠FCB ,
∵BF、CF分别平分∠ABC和∠ACB ,
∴∠EBF=∠FBC , ∠GCF=∠FCB ,
∴∠EBF=∠EFB , ∠GFC=∠GCF ,
∴EF=EB , FG=GC ,
∴△AEG的周长=AE+EF+FG+AG=AE+EB+AG+GC=AB+AC=9+11=20
故答案为:B.
7.【答案】 B
解:如图,过A作AE⊥BC,
∵△ABC是等腰三角形,
∴∠BAE=∠CAE=∠BAC,
∵CD⊥AB,
∠CBD=ABE,
∴∠BAE=∠BCD,
∴∠BCD=∠BAC.
故答案为:B.
8.【答案】 A
解:在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴, , ∠BAC+∠ABC+∠ACB=180°,
∴,
∴, 故②正确;
在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴∠OBC=∠OBE,∠OCB=∠OCF,
∵EF∥BC ,
∴∠OBC=∠EOB,∠OCB=∠FOC,
∴∠EOB=∠OBE,∠FOC=∠OCF,
∴BE=OE,CF=OF,
∴EF=OE+OF=BE+CF,故①正确;
如下图,过点O作OM⊥AB于点M,过点O作ON⊥BC于点N,连接OA,
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴ON=OD=OM=m,即:点O到△ABC各边的距离相等,故③正确;
∴, 故④错误.
故正确的是①②③.
故答案为:A.
二、填空题
9.【答案】 4
解:∵AB=AC,AD⊥BC,
∴BD=DC,
∵AB+AC+BC=18,
即AB+BD+CD+AC=18,
∴AC+DC=9,
又∵AC+DC+AD=13,
∴AD ,
故答案为:4.
10.【答案】 5
解:∵AB=AC , AD⊥BC ,
∴BD= BC= ×10=5cm.
故答案为:5.
11.【答案】 37
解:∵AD=AC,点E是CD中点,
∴AE⊥CD,
∴∠AEC=90°,
∴
∵AD=AC,
∴∠ADC=∠C=74°,
∵AD=BD,
∴2∠B=∠ADC=74°,
∴∠B=37°,
故答案为:37.
12.【答案】 50°、80°或65
解:在P运动的过程中有三种情况,分别求解.
第一种情况,当AO为等腰三角形底边时,得AP=PO,
∴∠A=∠AON=50°;
第二种情况,当PO为等腰三角形底边时,得AP=AO,
∴∠APO=∠AON=50°
∴∠A=80°;
第三种情况,当AP为等腰三角形底边时,得PO=AO,
∴∠A= .
故答案为:50°、80°或65°.
13.【答案】 2、7或8.
解:∵AB=10,点Q是BA的中点,
∴AQ=BQ= BA= ×10=5,
∵四边形ABCD是矩形,
∴DC=AB=10,∠B=∠C=∠D=90°,
①如图1,PQ=AQ=5时,过点P作PE⊥BA于E,
根据勾股定理,QE= ,
∴BE=BQ+QE=5+3=8,
∴CP=BE=8;
②如图2,AP=AQ=5时,
根据勾股定理,DP= ,
∴CP=10-3=7;
③如图3,PQ=AQ=5且△PBQ为钝角三角形时,过点P作PE⊥BA于E,
根据勾股定理:QE= ,
∵BE=QB-EQ=5-3=2,
∴CP=BE=2,
综上所述,CP的长为2或7或8.
故答案为:2、7或8.
三、解答题
14.【答案】 证明:∵AB//CD:.∠DCA=∠CAB
∵AC平分∠DAB.:.∠DAC=∠CAB
:.∠DCA=∠DAC
:.AD=CD即△ADC是等腰三角形。
15.【答案】 证明:过O作OD⊥AB于D,作OE⊥AC于E,
∵∠1=∠2, ∴OB=OC,
∵AO平分∠BAC, ∴OD=OE,
∴RTΔODB≌RTΔOEC(HL),
∴∠ABO=∠ACO,
∴∠ABO+∠1=∠ACO+∠2,
即∠ABC=∠ACB,
∴AB=AC, ∴ΔABC是等腰三角形.
16.【答案】 证明:作AF⊥BC于F,
∵AB=AC(已知),
∴BF=CF(三线合一),
又∵AD=AE(已知),
∴DF=EF(三线合一),
∴BF-DF=CF-EF,即BD=CE(等式的性质).
一、单选题
1.在等腰三角形ABC中,它的两边长分别为8cm和4cm,则它的周长为( ??)
A.?10cm?????????????????????????????B.?12 cm?????????????????????????????C.?20 cm或16 cm?????????????????????????????D.?20 cm
2.如果等腰三角形的一个外角为140°,那么底角为(?? )
A.?40°????????????????????????????????????B.?60°????????????????????????????????????C.?70°????????????????????????????????????D.?40°或70°
3.下列说法正确的是(?? )
A.?等腰三角形的角平分线、中线和高三线重合????????B.?等角对等边
C.?等腰三角形一定是锐角三角形?????????????????????????????D.?等腰三角形两个底角相等
4.已知 是 的两边,且 ,则 的形状是(? )
A.?等腰三角形?????????????????????????B.?等边三角形?????????????????????????C.?锐角三角形?????????????????????????D.?不确定
5.如图,在平面直角坐标系中,点A的坐标为 ,在x轴上确定点P,使 为等腰三角形,则符合条件的点P有(? )
A.?2个???????????????????????????????????????B.?3个???????????????????????????????????????C.?4个???????????????????????????????????????D.?5个
6.如图,在△ABC中,BF、CF分别平分∠ABC和∠ACB , 过点F作EG∥BC分别交于点AB、AC于点E、G . 若AB=9,BC=10,AC=11,则△AEG的周长为( )
A.?15?????????????????????????????????????????B.?20?????????????????????????????????????????C.?21?????????????????????????????????????????D.?19
7.等腰三角形一腰上的高与底边所夹的角( )
A.?等于顶角?????????????????B.?等于顶角的一半?????????????????C.?等于顶角的2倍?????????????????D.?等于底角的一半
8.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC 交AB于点E,交AC于点F,过点O作OD⊥AC于点D,下列四个结论:①EF=BE+CF; ②∠BOC=90°+ ∠A;③点O到△ABC各边的距离相等;④设OD=m,AE+AF=n,则S△AEF=mn.
其中正确的结论是(???? )
A.?①②③????????????????????????????????B.?①②④????????????????????????????????C.?②③④????????????????????????????????D.?①③④
二、填空题
9.如图,△ABC的周长为18,且AB=AC,AD⊥BC于D,△ACD的周长为13,那么AD的长为________.
10.在△ABC 中,AB=AC,AD⊥BC,BC=10cm, 则 BD=________ cm.
11.如图,△ABC中.点D在BC边上,BD=AD=AC,E为CD的中点.若∠CAE=16°,则∠B为________度.
12.如图,已知点P是射线 上一动点, 若 为等腰三角形,则 ________.
13.如图,矩形ABCD中,AB=10,BC=4,Q为AB边的中点,P为CD边上的动点,且△AQP是腰长为5的等腰三角形,则CP的长为________.
三、解答题
14.如图,已知AB∥CD,AC平分∠DAB.
求证:△ADC是等腰三角形.
15.已知:如图,OA平分∠BAC,∠1=∠2.
求证:△ABC是等腰三角形.
16.已知:如图, AB=AC,AD=AE.求证:BD=CE.
答案解析部分
一、单选题
1.【答案】 D
解:①当腰是4,底边是8时,4+4=8,不满足三角形的三边关系,因此舍去.
②当底边是4,腰长是8时,能构成三角形,则其周长=8+8+4=20.
故答案为:D.
2.【答案】 D
解:∵外角为140°,∴与它相邻的内角是180°﹣140°=40°;
①当40°是顶角时,底角是(180°﹣40°)÷2=70°;②当40°是底角时,底角是40°.
故答案为:D.
3.【答案】 D
解: A:等腰三角形的顶角平分线、底边上的中线和高三线重合,不符合题意;
B、?在同一三角形中等角对等边,不符合题意;
C、 等腰三角形不一定是锐角三角形,如顶角是120°,底角为30°的等腰三角形,不符合题意;
D、 等腰三角形两个底角相等,正确,符合题意;
故答案为:D.
4.【答案】 A
解:因为: ,所以: ,
所以: ,所以三角形ABC是等腰三角形,
故答案为:A.
5.【答案】 C
解:如图,
,
当AO=OP1 , AO=OP3时,P1(﹣ ,0),P3( ,0),
当AP2=OP2时,P2(1,0),
当AO=AP4时,P4(2,0),
故符合条件的点有4个.
故答案为:C.
6.【答案】 B
解:∵EG∥BC ,
∴∠EFB=∠FBC , ∠GFC=∠FCB ,
∵BF、CF分别平分∠ABC和∠ACB ,
∴∠EBF=∠FBC , ∠GCF=∠FCB ,
∴∠EBF=∠EFB , ∠GFC=∠GCF ,
∴EF=EB , FG=GC ,
∴△AEG的周长=AE+EF+FG+AG=AE+EB+AG+GC=AB+AC=9+11=20
故答案为:B.
7.【答案】 B
解:如图,过A作AE⊥BC,
∵△ABC是等腰三角形,
∴∠BAE=∠CAE=∠BAC,
∵CD⊥AB,
∠CBD=ABE,
∴∠BAE=∠BCD,
∴∠BCD=∠BAC.
故答案为:B.
8.【答案】 A
解:在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴, , ∠BAC+∠ABC+∠ACB=180°,
∴,
∴, 故②正确;
在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴∠OBC=∠OBE,∠OCB=∠OCF,
∵EF∥BC ,
∴∠OBC=∠EOB,∠OCB=∠FOC,
∴∠EOB=∠OBE,∠FOC=∠OCF,
∴BE=OE,CF=OF,
∴EF=OE+OF=BE+CF,故①正确;
如下图,过点O作OM⊥AB于点M,过点O作ON⊥BC于点N,连接OA,
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴ON=OD=OM=m,即:点O到△ABC各边的距离相等,故③正确;
∴, 故④错误.
故正确的是①②③.
故答案为:A.
二、填空题
9.【答案】 4
解:∵AB=AC,AD⊥BC,
∴BD=DC,
∵AB+AC+BC=18,
即AB+BD+CD+AC=18,
∴AC+DC=9,
又∵AC+DC+AD=13,
∴AD ,
故答案为:4.
10.【答案】 5
解:∵AB=AC , AD⊥BC ,
∴BD= BC= ×10=5cm.
故答案为:5.
11.【答案】 37
解:∵AD=AC,点E是CD中点,
∴AE⊥CD,
∴∠AEC=90°,
∴
∵AD=AC,
∴∠ADC=∠C=74°,
∵AD=BD,
∴2∠B=∠ADC=74°,
∴∠B=37°,
故答案为:37.
12.【答案】 50°、80°或65
解:在P运动的过程中有三种情况,分别求解.
第一种情况,当AO为等腰三角形底边时,得AP=PO,
∴∠A=∠AON=50°;
第二种情况,当PO为等腰三角形底边时,得AP=AO,
∴∠APO=∠AON=50°
∴∠A=80°;
第三种情况,当AP为等腰三角形底边时,得PO=AO,
∴∠A= .
故答案为:50°、80°或65°.
13.【答案】 2、7或8.
解:∵AB=10,点Q是BA的中点,
∴AQ=BQ= BA= ×10=5,
∵四边形ABCD是矩形,
∴DC=AB=10,∠B=∠C=∠D=90°,
①如图1,PQ=AQ=5时,过点P作PE⊥BA于E,
根据勾股定理,QE= ,
∴BE=BQ+QE=5+3=8,
∴CP=BE=8;
②如图2,AP=AQ=5时,
根据勾股定理,DP= ,
∴CP=10-3=7;
③如图3,PQ=AQ=5且△PBQ为钝角三角形时,过点P作PE⊥BA于E,
根据勾股定理:QE= ,
∵BE=QB-EQ=5-3=2,
∴CP=BE=2,
综上所述,CP的长为2或7或8.
故答案为:2、7或8.
三、解答题
14.【答案】 证明:∵AB//CD:.∠DCA=∠CAB
∵AC平分∠DAB.:.∠DAC=∠CAB
:.∠DCA=∠DAC
:.AD=CD即△ADC是等腰三角形。
15.【答案】 证明:过O作OD⊥AB于D,作OE⊥AC于E,
∵∠1=∠2, ∴OB=OC,
∵AO平分∠BAC, ∴OD=OE,
∴RTΔODB≌RTΔOEC(HL),
∴∠ABO=∠ACO,
∴∠ABO+∠1=∠ACO+∠2,
即∠ABC=∠ACB,
∴AB=AC, ∴ΔABC是等腰三角形.
16.【答案】 证明:作AF⊥BC于F,
∵AB=AC(已知),
∴BF=CF(三线合一),
又∵AD=AE(已知),
∴DF=EF(三线合一),
∴BF-DF=CF-EF,即BD=CE(等式的性质).
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
