人教版数学七年级上册 3.4 实际问题与一元二次方程——电话计费问题课件(22张)
文档属性
| 名称 | 人教版数学七年级上册 3.4 实际问题与一元二次方程——电话计费问题课件(22张) |

|
|
| 格式 | zip | ||
| 文件大小 | 162.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-19 00:00:00 | ||
图片预览




文档简介
(共22张PPT)
3.4
实际问题与一元一次方程
探究3
电话计费问题
1.
体会分类思想和方程思想在解决问题中的作用,能够根据已知条件选择分类关键点对“电话计费问题”进行整体分析,从而得出整体选择方案.
(重点、难点)
2.
进一步深化对数学建模方法的体验,增强应用方程模型解决问题的意识和能力.(重点)
学习目标
(一)对问题的初步探究
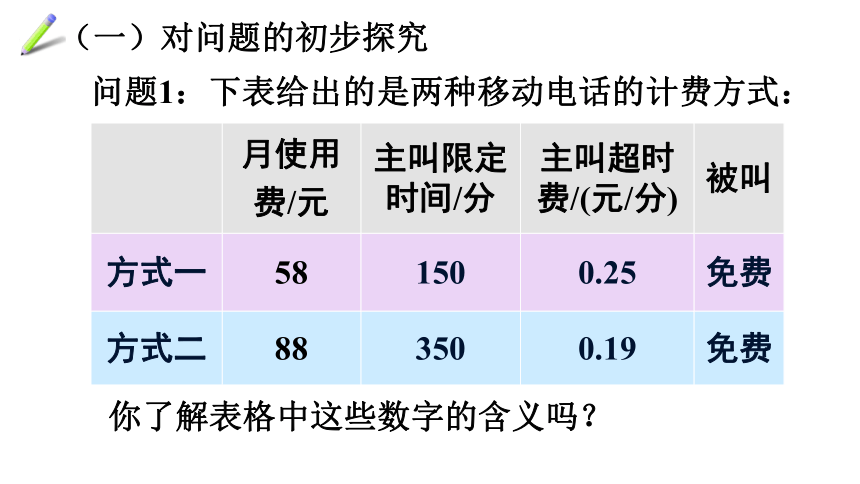
问题1:下表给出的是两种移动电话的计费方式:
你了解表格中这些数字的含义吗?
免费
0.19
350
88
方式二
免费
0.25
150
58
方式一
被叫
主叫超时费/(元/分)
主叫限定时间/分
月使用
费/元
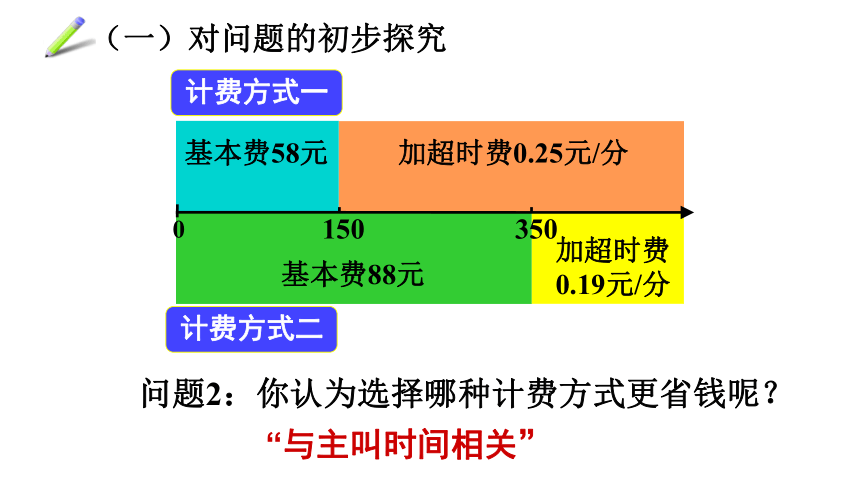
问题2:你认为选择哪种计费方式更省钱呢?
“与主叫时间相关”
加超时费0.19元/分
基本费88元
加超时费0.25元/分
基本费58元
350
0
150
计费方式一
计费方式二
(一)对问题的初步探究
(二)对问题的深入探究
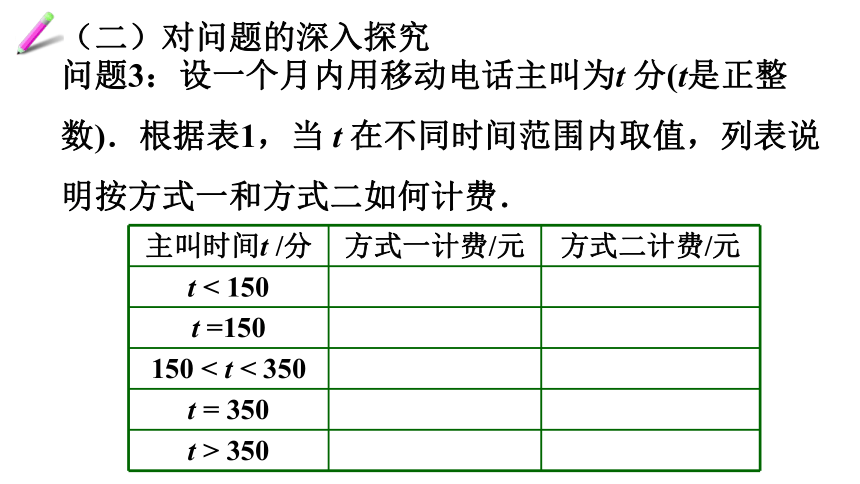
问题3:设一个月内用移动电话主叫为t
分(t是正整数).根据表1,当
t
在不同时间范围内取值,列表说明按方式一和方式二如何计费.
主叫时间t
/分
方式一计费/元
方式二计费/元
t
<
150
t
=150
150
<
t
<
350
t
=
350
t
>
350
主叫时间t
/分
方式一计费/元
方式二计费/元
t
<
150
58
88
t
=
150
58
88
150
<
t
<
350
58+0.25(t-150)
88
t
=
350
58+0.25×(350-150)=108
88
t
>
350
58+0.25(t-150)
88+0.19(t-350)
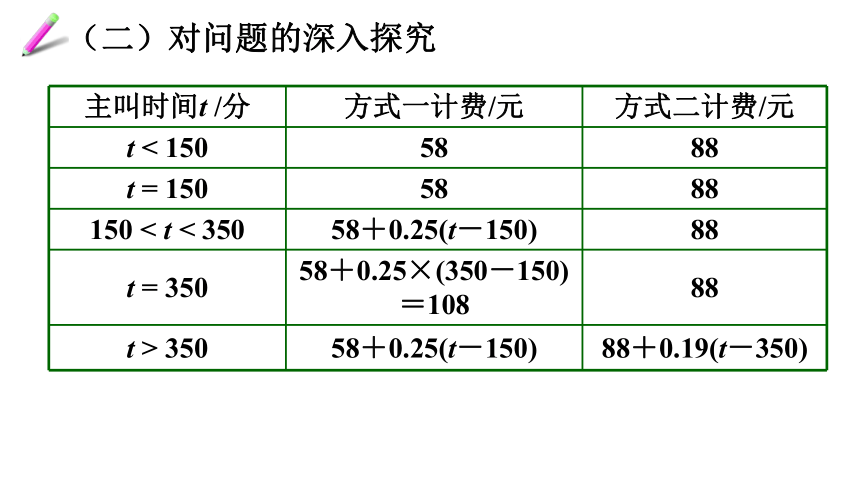
(二)对问题的深入探究
主叫时间t
/分
方式一计费/元
方式二计费/元
t
<
150
58
88
t
=
150
58
88
150
<
t
<
350
58+0.25(t-150)
88
t
=
350
108
88
t
>
350
58+0.25(t-150)
88+0.19(t-350)
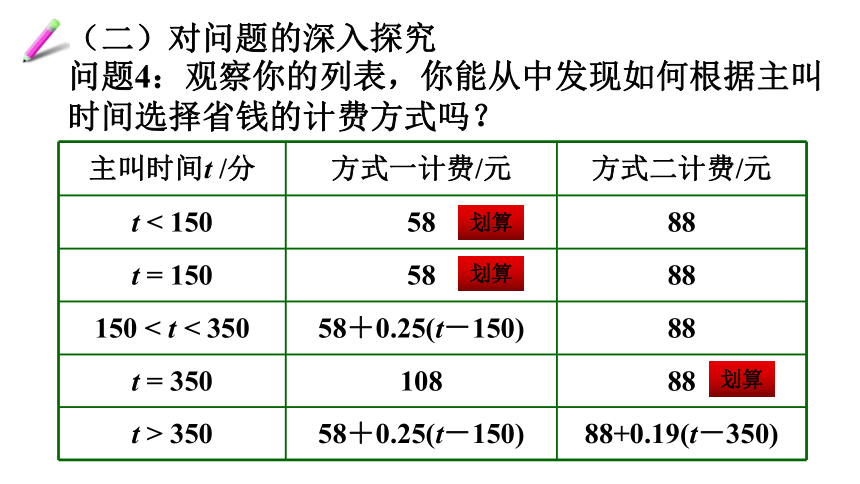
问题4:观察你的列表,你能从中发现如何根据主叫时间选择省钱的计费方式吗?
(二)对问题的深入探究
划算
划算
划算
主叫时间t
/分
方式一计费/元
方式二计费/元
150
<
t
<
350
58+0.25(t-150)
88
依题意得:58+0.25(t-150)
=
88
去括号得:58+0.25t-37.5
=
88
移项、合并同类项得:
0.25t
=
67.5
系数化1得:
t
=270
∴当
t
=270分时,两种计费方式的费用相等,
那么当150<
t
<270分和270<
t
<350分时,两种计费方式哪种更合算呢?
(二)对问题的深入探究
(1)当150<
t
<270分时,按方式一分计费少于按
方式二的计费;
(2)当270<
t
<350分时,按方式一的计费多于按
方式二的计费;
(二)对问题的深入探究
主叫时间t
/分
方式一计费/元
方式二计费/元
t
>350
58+0.25(t-150)
88+0.19(t-350)
当t
>350分时,两种计费方式哪种更合算呢?
=108+0.25(t-350)
(二)对问题的深入探究
问题4:综合以上的分析,可以发现:
时,选择方式一省钱;
时,选择方式二省钱.
0
计费方式一
计费方式二
270
t
<
270
t
>
270
(二)对问题的深入探究
(三)归纳小结
请回顾电话计费问题的探究过程,并回答以下问题:
(1)电话计费问题的核心问题是什么?
(2)探究解题的过程大致包含哪几个步骤?
(3)我们在探究过程中用到了哪些方法,你有哪些收获?
1.确定分段点再分情况
2.运用方程确定何时计费相等
1.确定分段点
2.分情况考虑
3.确定何时计费相等
4.写出答案
移动公司推出两种智能手机上网流量包:
月使用费(元)
含上网流量(M)
流量超出部分(元/M)
A种
30
320
0.2
B种
50
550
0.1
如何选择流量包更划算?
(四)变式练习
解:设一个月内使用的流量为
x
M,根据题意,当x
在不同范围内取值时,两种流量包计费如下表:
使用流量
x(M)
A种计费(元)
B种计费(元)
x
≤
320
30
50
320
<
x
<
550
30+0.2(x-320)
50
x
=
550
76
50
x
>
550
30+0.2(x-320)
50+0.1(x-550)
(1)
当
x
≤
320
时,流量包A
计费少(30元);
(2)
当
320<x<420
时,流量包A
计费少(<50元);
(3)
当
x
=
420时,两种流量包计费相等,都是50元;
(4)
当
420<x<550
时,流量包B
计费少(50元);
(5)
当
x
=
550
时,流量包B
计费少(50元);
(6)
当
x>550
时,流量包B
计费少.
综上所述,
当月使用流量小于
420
M
时,选择流量包A
划算;
当月使用流量等于
420
M
时,两种流量包费用一样;
当月使用流量大于
420
M
时,选择流量包B
划算.
(五)巩固应用
用A4纸在某打印社复印文件,复印页数不超过20时,每页收费0.12元;复印页数超过20时,超过部分每页收费0.09元.
在某图书馆复印同样的文件,不论复印多少页,每页收费0.1元.
如何根据复印的页数选择复印的地点使总价格比较便宜?(复印的页数不为零)
复印页数x
打印社复印费用/元
图书馆复印费用/元
x
<20
0.12x
0.1x
x
=20
0.12×20=2.4
0.1×20=2
x
>20
2.4+0.09(x-20)
0.1x
解:依题意列表得:
(1)当
x
<
20时,0.12
x
>
0.1
x
恒成立,图书馆
价格便宜;
(2)当
x
=
20时,2.4
>
2,图书馆价格便宜;
(3)当
x
>
20时,
依题意得:2.4+0.09(x-20)=0.1x
解得:
x=60
∴
当20
<
x
<
60时,图书馆价格便宜;
当x
>
60时,打印社价格便宜.
综上所述:当x
<
60时,图书馆价格便宜;当x
>
60时,打印社价格便宜.
1.小明所在城市的“阶梯水价”收费办法是:每户用水不超过5吨,每吨水费x元;超过5吨,超过部分每吨加收2元,小明家今年5月份用水9吨,共交水费为44元,根据题意列出关于x的方程正确的是( )
A.5x+4(x+2)=44
B.5x+4(x-2)=44
C.9(x+2)=44
D.9(x+2)-4×2=44
当堂练习
2.
某市为鼓励居民节约用水,对自来水用户按分段计费方式收取水费:若每户每月用水不超过
7m3,则按
2
元/m3
收费;若每户每月用水超过
7
m3,则超过的部分按
3元/m3
收费.
如果某居民户去年12月缴纳了
53
元水费,那么这户居民去年12月的用水量为_______m3.
20
课堂小结
1.
解决电话计费问题需要明确“哪种计费方式更省钱”与“主叫时间”有关.
2.
此类问题的关键是能够根据已知条件找到合适的分段点,然后建立方程模型分类讨论,从而得出整体选择方案.
(六)布置作业
《基础训练》P59第14题、P64第25、26题
3.4
实际问题与一元一次方程
探究3
电话计费问题
1.
体会分类思想和方程思想在解决问题中的作用,能够根据已知条件选择分类关键点对“电话计费问题”进行整体分析,从而得出整体选择方案.
(重点、难点)
2.
进一步深化对数学建模方法的体验,增强应用方程模型解决问题的意识和能力.(重点)
学习目标
(一)对问题的初步探究
问题1:下表给出的是两种移动电话的计费方式:
你了解表格中这些数字的含义吗?
免费
0.19
350
88
方式二
免费
0.25
150
58
方式一
被叫
主叫超时费/(元/分)
主叫限定时间/分
月使用
费/元
问题2:你认为选择哪种计费方式更省钱呢?
“与主叫时间相关”
加超时费0.19元/分
基本费88元
加超时费0.25元/分
基本费58元
350
0
150
计费方式一
计费方式二
(一)对问题的初步探究
(二)对问题的深入探究
问题3:设一个月内用移动电话主叫为t
分(t是正整数).根据表1,当
t
在不同时间范围内取值,列表说明按方式一和方式二如何计费.
主叫时间t
/分
方式一计费/元
方式二计费/元
t
<
150
t
=150
150
<
t
<
350
t
=
350
t
>
350
主叫时间t
/分
方式一计费/元
方式二计费/元
t
<
150
58
88
t
=
150
58
88
150
<
t
<
350
58+0.25(t-150)
88
t
=
350
58+0.25×(350-150)=108
88
t
>
350
58+0.25(t-150)
88+0.19(t-350)
(二)对问题的深入探究
主叫时间t
/分
方式一计费/元
方式二计费/元
t
<
150
58
88
t
=
150
58
88
150
<
t
<
350
58+0.25(t-150)
88
t
=
350
108
88
t
>
350
58+0.25(t-150)
88+0.19(t-350)
问题4:观察你的列表,你能从中发现如何根据主叫时间选择省钱的计费方式吗?
(二)对问题的深入探究
划算
划算
划算
主叫时间t
/分
方式一计费/元
方式二计费/元
150
<
t
<
350
58+0.25(t-150)
88
依题意得:58+0.25(t-150)
=
88
去括号得:58+0.25t-37.5
=
88
移项、合并同类项得:
0.25t
=
67.5
系数化1得:
t
=270
∴当
t
=270分时,两种计费方式的费用相等,
那么当150<
t
<270分和270<
t
<350分时,两种计费方式哪种更合算呢?
(二)对问题的深入探究
(1)当150<
t
<270分时,按方式一分计费少于按
方式二的计费;
(2)当270<
t
<350分时,按方式一的计费多于按
方式二的计费;
(二)对问题的深入探究
主叫时间t
/分
方式一计费/元
方式二计费/元
t
>350
58+0.25(t-150)
88+0.19(t-350)
当t
>350分时,两种计费方式哪种更合算呢?
=108+0.25(t-350)
(二)对问题的深入探究
问题4:综合以上的分析,可以发现:
时,选择方式一省钱;
时,选择方式二省钱.
0
计费方式一
计费方式二
270
t
<
270
t
>
270
(二)对问题的深入探究
(三)归纳小结
请回顾电话计费问题的探究过程,并回答以下问题:
(1)电话计费问题的核心问题是什么?
(2)探究解题的过程大致包含哪几个步骤?
(3)我们在探究过程中用到了哪些方法,你有哪些收获?
1.确定分段点再分情况
2.运用方程确定何时计费相等
1.确定分段点
2.分情况考虑
3.确定何时计费相等
4.写出答案
移动公司推出两种智能手机上网流量包:
月使用费(元)
含上网流量(M)
流量超出部分(元/M)
A种
30
320
0.2
B种
50
550
0.1
如何选择流量包更划算?
(四)变式练习
解:设一个月内使用的流量为
x
M,根据题意,当x
在不同范围内取值时,两种流量包计费如下表:
使用流量
x(M)
A种计费(元)
B种计费(元)
x
≤
320
30
50
320
<
x
<
550
30+0.2(x-320)
50
x
=
550
76
50
x
>
550
30+0.2(x-320)
50+0.1(x-550)
(1)
当
x
≤
320
时,流量包A
计费少(30元);
(2)
当
320<x<420
时,流量包A
计费少(<50元);
(3)
当
x
=
420时,两种流量包计费相等,都是50元;
(4)
当
420<x<550
时,流量包B
计费少(50元);
(5)
当
x
=
550
时,流量包B
计费少(50元);
(6)
当
x>550
时,流量包B
计费少.
综上所述,
当月使用流量小于
420
M
时,选择流量包A
划算;
当月使用流量等于
420
M
时,两种流量包费用一样;
当月使用流量大于
420
M
时,选择流量包B
划算.
(五)巩固应用
用A4纸在某打印社复印文件,复印页数不超过20时,每页收费0.12元;复印页数超过20时,超过部分每页收费0.09元.
在某图书馆复印同样的文件,不论复印多少页,每页收费0.1元.
如何根据复印的页数选择复印的地点使总价格比较便宜?(复印的页数不为零)
复印页数x
打印社复印费用/元
图书馆复印费用/元
x
<20
0.12x
0.1x
x
=20
0.12×20=2.4
0.1×20=2
x
>20
2.4+0.09(x-20)
0.1x
解:依题意列表得:
(1)当
x
<
20时,0.12
x
>
0.1
x
恒成立,图书馆
价格便宜;
(2)当
x
=
20时,2.4
>
2,图书馆价格便宜;
(3)当
x
>
20时,
依题意得:2.4+0.09(x-20)=0.1x
解得:
x=60
∴
当20
<
x
<
60时,图书馆价格便宜;
当x
>
60时,打印社价格便宜.
综上所述:当x
<
60时,图书馆价格便宜;当x
>
60时,打印社价格便宜.
1.小明所在城市的“阶梯水价”收费办法是:每户用水不超过5吨,每吨水费x元;超过5吨,超过部分每吨加收2元,小明家今年5月份用水9吨,共交水费为44元,根据题意列出关于x的方程正确的是( )
A.5x+4(x+2)=44
B.5x+4(x-2)=44
C.9(x+2)=44
D.9(x+2)-4×2=44
当堂练习
2.
某市为鼓励居民节约用水,对自来水用户按分段计费方式收取水费:若每户每月用水不超过
7m3,则按
2
元/m3
收费;若每户每月用水超过
7
m3,则超过的部分按
3元/m3
收费.
如果某居民户去年12月缴纳了
53
元水费,那么这户居民去年12月的用水量为_______m3.
20
课堂小结
1.
解决电话计费问题需要明确“哪种计费方式更省钱”与“主叫时间”有关.
2.
此类问题的关键是能够根据已知条件找到合适的分段点,然后建立方程模型分类讨论,从而得出整体选择方案.
(六)布置作业
《基础训练》P59第14题、P64第25、26题
