沪科版(2012)初中数学八年级下册 19.3.4 菱形的判定 课件(19张)
文档属性
| 名称 | 沪科版(2012)初中数学八年级下册 19.3.4 菱形的判定 课件(19张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 325.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-19 00:00:00 | ||
图片预览




文档简介
19.3.2 菱形的判定
第19章 四边形
根据菱形的定义,可得:
∵四边形ABCD是平行四边形
且AB=AD
∴四边形ABCD是菱形
数学语言:
有一组邻边相等的平行四边形叫做菱形。
先画两条等长的线段AB、AD,然后分别以B、D为圆心,AB为半径画弧,得到两弧的交点C,连接BC、CD,就得到了一个四边形,猜一猜,这是什么四边形?说出你的理由
猜想:四边都相等的四边形是菱形。
A
B
C
D
O
情境引入
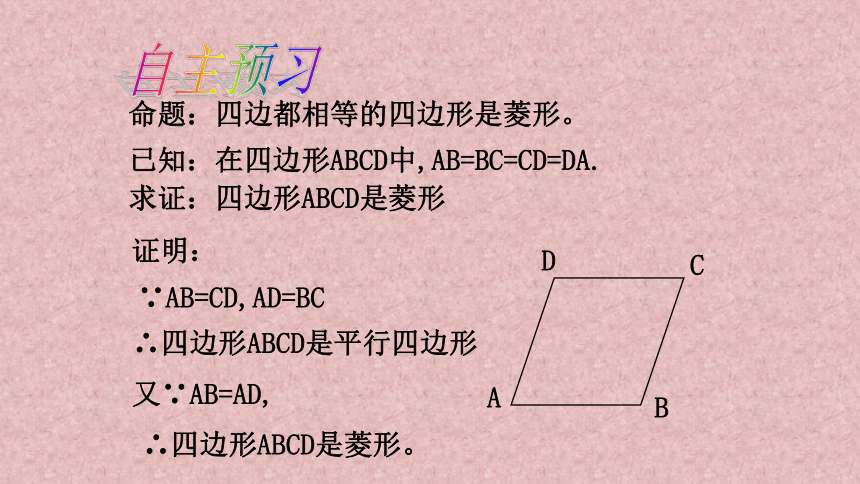
命题:四边都相等的四边形是菱形。
已知:在四边形ABCD中,AB=BC=CD=DA.
求证:四边形ABCD是菱形
D
A
B
C
证明:
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
又∵AB=AD,
∴四边形ABCD是菱形。
自主预习
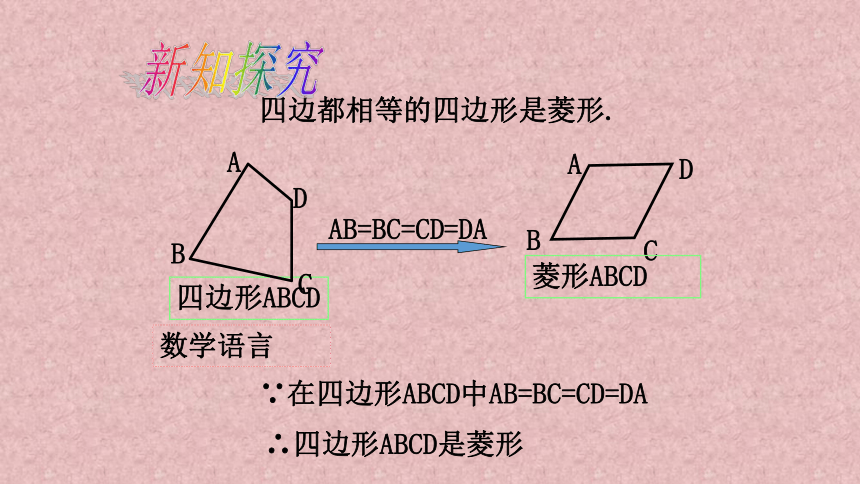
四边都相等的四边形是菱形.
AB=BC=CD=DA
A
B
C
D
菱形ABCD
∵在四边形ABCD中AB=BC=CD=DA
∴四边形ABCD是菱形
四边形ABCD
A
B
C
D
数学语言
新知探究
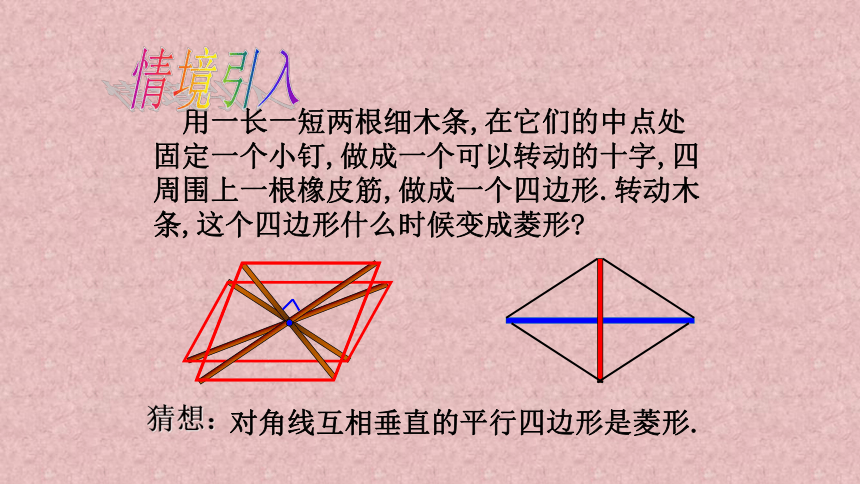
用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个四边形.转动木条,这个四边形什么时候变成菱形?
猜想:
对角线互相垂直的平行四边形是菱形.
情境引入
命题:对角线互相垂直的平行四边形是菱形.
已知:在 中,AC ⊥ BD
ABCD
ABCD
求证: 是菱形
A
B
C
D
O
∟
证明:
∵四边形ABCD是平行四边形
∴OA=OC
又∵AC⊥BD;
∴BA=BC
新知探究
∴ ABCD是菱形。
对角线互相垂直的平行四边形是菱形
AC⊥BD
∵在□ABCD中,AC⊥BD
∴ □ABCD是菱形。
A
B
C
D
菱形ABCD
A
B
C
D
□ABCD
几何语言:
菱形常用的判定方法:
有一组邻边相等的平行四边形叫做菱形
对角线互相垂直的平行四边形是菱形
四边都相等的四边形是菱形
+邻边相等 =
+对角线线互相垂直=
四条边相等+ =
知识梳理
1.老师说下列三个图形都是菱形,你相信吗?
5
5
3
4
3
4
5
5
5
5
有一组邻边相等的平行四边形叫做菱形
对角线互相垂直的平行四边形是菱形
四边都相等的四边形是菱形。
3
3
4
4
┍
随堂练习
2、将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,想一想,红色的部分展开后,应该是什么图形?为什么?
3.判断下列说法是否正确?为什么?
(1)对角线互相垂直的四边形是菱形; ( )
(2)对角线互相垂直平分的四边形是菱形;( )
(3)对角线互相垂直,且有一组邻边相等
的四边形是菱形; ( )
(4)两条邻边相等,且一条对角线平分一
组对角的四边形是菱形. ( )
╳
√
╳
╳
∟
A
D
B
C
∟
A
B
C
D
A
B
C
D
O
∴四边形ABCD是菱形.
∴OA=OC=4 OB=OD=3
解:
又∵AB=5
即AO⊥BO
∴∠AOB=90°
∴ AD=AB=5.
∵ 四边形ABCD是平行四边形
∴AB2=AO2+BO2
例6 如图,在 ABCD中,AB=5,AC=8,DB=6。
求AD的长。
5.已知: ABCD的对角线AC的垂直平分线与边AD 、BC分别交于E、F
求证:四边形AFCE是菱形。
B
D
C
F
E
A
O
例、把两张等宽的纸条交叉重叠在一起,试探究重叠部分ABCD的形状,并说明理由。
A
C
D
B
解:重叠部分为菱形,理由如下:
过点A作AE⊥BC于E,AF⊥CD于F
∠AEB=∠AFD=900
因纸条等宽,故AE=AF
又 AB∥CD,AD∥BC
∴四边形ABCD为平行四边形
∴∠ABE=∠ADF
∴△ABE≌△ADF(A.A.S)
∴AB=AD
∴四边形ABCD是菱形。
E
F
菱形的判定:
一组邻边相等的平行四边形是菱形.
对角线互相垂直的平行四边形是菱形.
四条边都相等的四边形是菱形.
小结:
四条边都相等
菱形
一组邻边相等
对角线互相垂直
对角线互相平分
一组对边平行且相等
两组对边分别平行或相等
总结对比
四边形
平行四边形
两组对角分别相等
第19章 四边形
根据菱形的定义,可得:
∵四边形ABCD是平行四边形
且AB=AD
∴四边形ABCD是菱形
数学语言:
有一组邻边相等的平行四边形叫做菱形。
先画两条等长的线段AB、AD,然后分别以B、D为圆心,AB为半径画弧,得到两弧的交点C,连接BC、CD,就得到了一个四边形,猜一猜,这是什么四边形?说出你的理由
猜想:四边都相等的四边形是菱形。
A
B
C
D
O
情境引入
命题:四边都相等的四边形是菱形。
已知:在四边形ABCD中,AB=BC=CD=DA.
求证:四边形ABCD是菱形
D
A
B
C
证明:
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
又∵AB=AD,
∴四边形ABCD是菱形。
自主预习
四边都相等的四边形是菱形.
AB=BC=CD=DA
A
B
C
D
菱形ABCD
∵在四边形ABCD中AB=BC=CD=DA
∴四边形ABCD是菱形
四边形ABCD
A
B
C
D
数学语言
新知探究
用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个四边形.转动木条,这个四边形什么时候变成菱形?
猜想:
对角线互相垂直的平行四边形是菱形.
情境引入
命题:对角线互相垂直的平行四边形是菱形.
已知:在 中,AC ⊥ BD
ABCD
ABCD
求证: 是菱形
A
B
C
D
O
∟
证明:
∵四边形ABCD是平行四边形
∴OA=OC
又∵AC⊥BD;
∴BA=BC
新知探究
∴ ABCD是菱形。
对角线互相垂直的平行四边形是菱形
AC⊥BD
∵在□ABCD中,AC⊥BD
∴ □ABCD是菱形。
A
B
C
D
菱形ABCD
A
B
C
D
□ABCD
几何语言:
菱形常用的判定方法:
有一组邻边相等的平行四边形叫做菱形
对角线互相垂直的平行四边形是菱形
四边都相等的四边形是菱形
+邻边相等 =
+对角线线互相垂直=
四条边相等+ =
知识梳理
1.老师说下列三个图形都是菱形,你相信吗?
5
5
3
4
3
4
5
5
5
5
有一组邻边相等的平行四边形叫做菱形
对角线互相垂直的平行四边形是菱形
四边都相等的四边形是菱形。
3
3
4
4
┍
随堂练习
2、将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,想一想,红色的部分展开后,应该是什么图形?为什么?
3.判断下列说法是否正确?为什么?
(1)对角线互相垂直的四边形是菱形; ( )
(2)对角线互相垂直平分的四边形是菱形;( )
(3)对角线互相垂直,且有一组邻边相等
的四边形是菱形; ( )
(4)两条邻边相等,且一条对角线平分一
组对角的四边形是菱形. ( )
╳
√
╳
╳
∟
A
D
B
C
∟
A
B
C
D
A
B
C
D
O
∴四边形ABCD是菱形.
∴OA=OC=4 OB=OD=3
解:
又∵AB=5
即AO⊥BO
∴∠AOB=90°
∴ AD=AB=5.
∵ 四边形ABCD是平行四边形
∴AB2=AO2+BO2
例6 如图,在 ABCD中,AB=5,AC=8,DB=6。
求AD的长。
5.已知: ABCD的对角线AC的垂直平分线与边AD 、BC分别交于E、F
求证:四边形AFCE是菱形。
B
D
C
F
E
A
O
例、把两张等宽的纸条交叉重叠在一起,试探究重叠部分ABCD的形状,并说明理由。
A
C
D
B
解:重叠部分为菱形,理由如下:
过点A作AE⊥BC于E,AF⊥CD于F
∠AEB=∠AFD=900
因纸条等宽,故AE=AF
又 AB∥CD,AD∥BC
∴四边形ABCD为平行四边形
∴∠ABE=∠ADF
∴△ABE≌△ADF(A.A.S)
∴AB=AD
∴四边形ABCD是菱形。
E
F
菱形的判定:
一组邻边相等的平行四边形是菱形.
对角线互相垂直的平行四边形是菱形.
四条边都相等的四边形是菱形.
小结:
四条边都相等
菱形
一组邻边相等
对角线互相垂直
对角线互相平分
一组对边平行且相等
两组对边分别平行或相等
总结对比
四边形
平行四边形
两组对角分别相等
