人教版八年级数学上册 13.3.2 等边三角形的性质与判定课件(15张)
文档属性
| 名称 | 人教版八年级数学上册 13.3.2 等边三角形的性质与判定课件(15张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 119.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-19 20:42:18 | ||
图片预览



文档简介
八年级数学·上 新课标 [人]
第十三章 轴对称
13.3.2 等边三角形(1)
导入新课
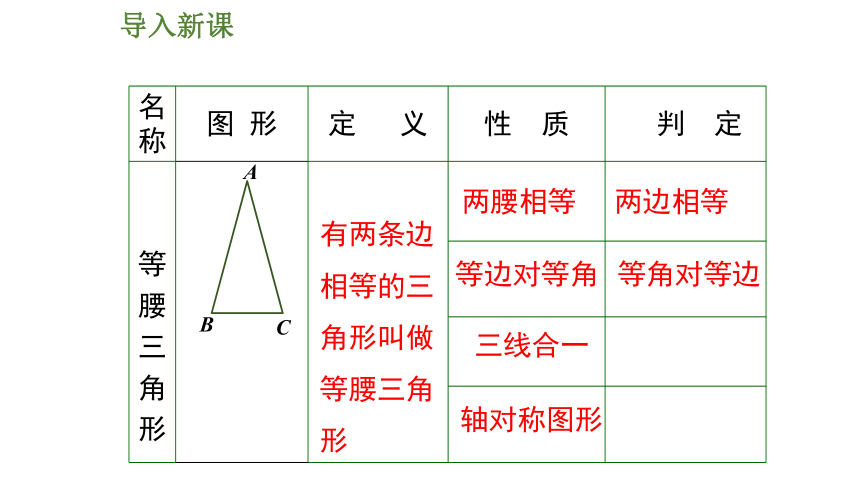
名称
图 形
定 义
性 质
判 定
等
腰
三
角
形
等边对等角
三线合一
等角对等边
两边相等
两腰相等
轴对称图形
A
B
C
有两条边相等的三角形叫做等腰三角形
等边三角形的定义
一
类比探究
等腰三角形
等边三角形
一般三角形
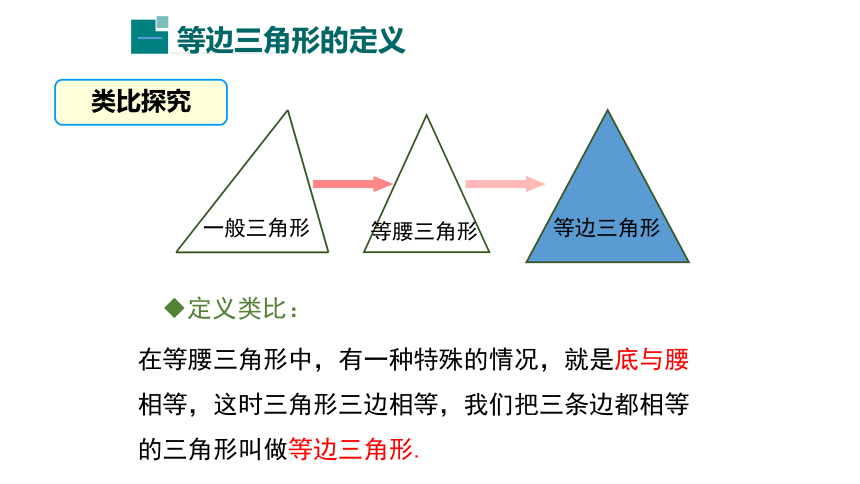
定义类比:
在等腰三角形中,有一种特殊的情况,就是底与腰相等,这时三角形三边相等,我们把三条边都相等的三角形叫做等边三角形.
等边三角形的性质
二
图形
等腰三角形
性 质
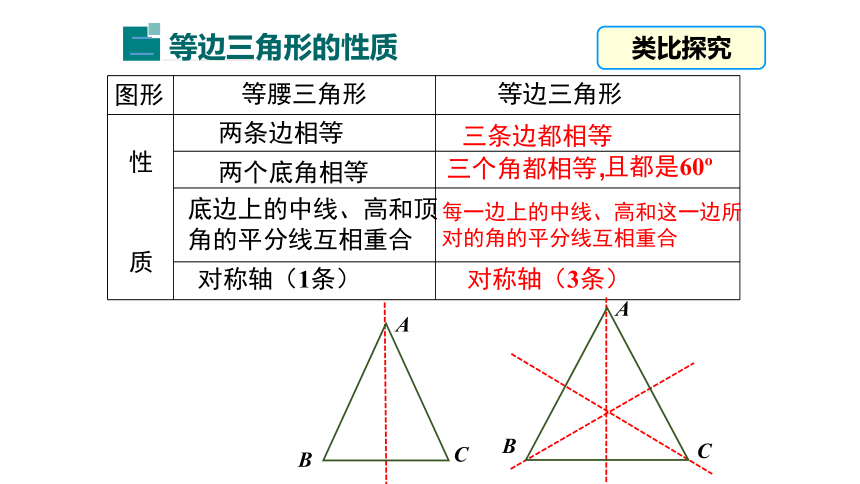
每一边上的中线、高和这一边所对的角的平分线互相重合
三个角都相等,
对称轴(3条)
等边三角形
对称轴(1条)
两个底角相等
底边上的中线、高和顶角的平分线互相重合
且都是60?
两条边相等
三条边都相等
A
B
C
A
B
C
类比探究
1、等边三角形的性质:
等边三角形的三个内角相等,并且每一个角都等于60°
把这个命题的文字语言转化为数学语言是:
已知:
求证:
△ABC是等边三角形
∠A=∠B=∠C=60°
A
C
B
类比探究
等边三角形的判定
三
图形
等腰三角形
判 定
三个角都相等的三角形是等边三角形
等边三角形
从角看:两个角相等的三角形是等腰三角形
从边看:两条边相等的三角形是等腰三角形
三条边都相等的三角形是等边三角形
小明认为还有第三种方法“两条边相等且有一个角是60°的三角形也是等边三角形”,你同意吗?
等边三角形的判定方法:
有一个角是60°的等腰三角形是等边三角形.
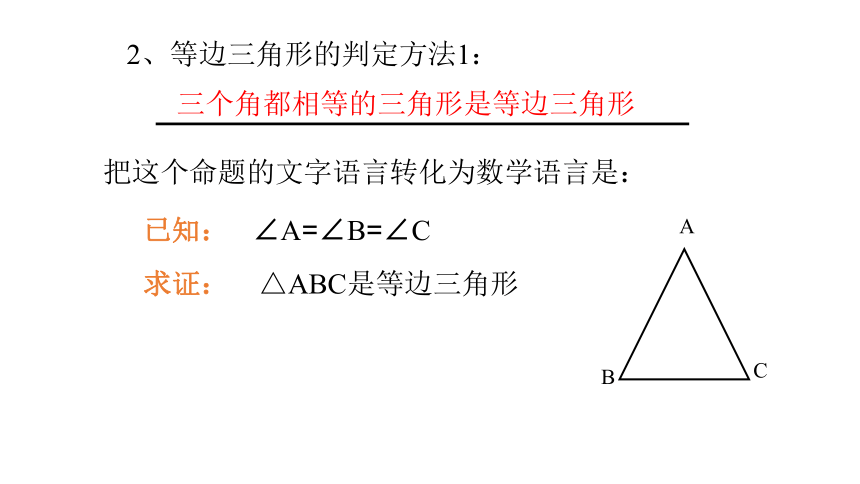
2、等边三角形的判定方法1:
三个角都相等的三角形是等边三角形
把这个命题的文字语言转化为数学语言是:
已知:
求证:
∠A=∠B=∠C
△ABC是等边三角形
A
B
C
3、等边三角形的判定方法2:
有一个角是60°的等腰三角形是等边三角形
已知:
求证:
△ABC是等腰三角形,若∠A=60°
△ABC是等边三角形
A
B
C
把这个命题的文字语言转化为数学语言是:
例1 如图,在等边三角形ABC中,DE∥BC, 求证:△ADE是等边三角形.
A
C
B
D
E
典例精析
证明:
∵ △ABC是等边三角形,
∴ ∠A= ∠B= ∠C.
∵ DE//BC,
∴ ∠ADE= ∠B, ∠ AED= ∠C.
∴ ∠A= ∠ADE= ∠ AED.
∴ △ADE是等边三角形.
想一想:本题还有其他证法吗?
变式:上题中,若将条件DE∥BC改为AD=AE, △ADE还是等边三角形吗?试说明理由.
A
C
B
D
E
如图,在等边三角形ABC中,AD=AE, 求证:△ADE是等边三角形.
1、下列四个说法中,不正确的有( )
①三个角都相等的三角形是等边三角形。
②有两个角等于60°的三角形是等边三角形.
③有一个角是60°的等腰三角形是等边三角形.
④有两个角相等的等腰三角形是等边三角形.
④
随堂练习
随堂练习
2、已知△ABC中,∠A=∠B=60°,AB=3cm
则△ABC的周长为________
3、△ABC是等腰三角形,周长为15cm且∠A=60°,
则BC=_______
4、如图,等边三角形ABC中,AD是BC上的高,
∠ BDE=∠CDF=60 °,
图中有哪些与BD相等的线段?
(书P80练习2)
9cm
5cm
BD=AE=BE=CD=CF=AF=DF=DE
B
C
D
A
E
5.如图,等边三角形ABC中,BD是AC边上的中线,BD=BE,求∠EDA的度数.
解:
∵ △ABC是等边三角形,
∴∠CBA=60°.
∵BD是AC边上的中线,
∴∠BDA=90°, ∠DBA=30 °.
∵ BD=BE,
∴ ∠BDE=(180 °- ∠DBA) ÷2 =(180°-30°) ÷2=75°.
∴ ∠EDA=90 °- ∠BDE=90°-75°=15°.
(1)等边三角形的性质:
小结:
1. 等边三角形的三边相等
2. 等边三角形的内角都相等,且都等于60 °
3. 等边三角形各边上中线,高和所对角的平分线都三线合一.
4. 等边三角形是轴对称图形,有三条对称轴
(2) 等边三角形的判定:
1.三边相等的三角形是等边三角形.
2.三个内角都等于60 °的三角形是等边三角形.
3.有一个内角等于60 °的等腰三角形是等边三角形.
学以致用
如图,△ABD,△AEC都是等边三角形。
求证:BE=DC
E
D
C
B
A
第十三章 轴对称
13.3.2 等边三角形(1)
导入新课
名称
图 形
定 义
性 质
判 定
等
腰
三
角
形
等边对等角
三线合一
等角对等边
两边相等
两腰相等
轴对称图形
A
B
C
有两条边相等的三角形叫做等腰三角形
等边三角形的定义
一
类比探究
等腰三角形
等边三角形
一般三角形
定义类比:
在等腰三角形中,有一种特殊的情况,就是底与腰相等,这时三角形三边相等,我们把三条边都相等的三角形叫做等边三角形.
等边三角形的性质
二
图形
等腰三角形
性 质
每一边上的中线、高和这一边所对的角的平分线互相重合
三个角都相等,
对称轴(3条)
等边三角形
对称轴(1条)
两个底角相等
底边上的中线、高和顶角的平分线互相重合
且都是60?
两条边相等
三条边都相等
A
B
C
A
B
C
类比探究
1、等边三角形的性质:
等边三角形的三个内角相等,并且每一个角都等于60°
把这个命题的文字语言转化为数学语言是:
已知:
求证:
△ABC是等边三角形
∠A=∠B=∠C=60°
A
C
B
类比探究
等边三角形的判定
三
图形
等腰三角形
判 定
三个角都相等的三角形是等边三角形
等边三角形
从角看:两个角相等的三角形是等腰三角形
从边看:两条边相等的三角形是等腰三角形
三条边都相等的三角形是等边三角形
小明认为还有第三种方法“两条边相等且有一个角是60°的三角形也是等边三角形”,你同意吗?
等边三角形的判定方法:
有一个角是60°的等腰三角形是等边三角形.
2、等边三角形的判定方法1:
三个角都相等的三角形是等边三角形
把这个命题的文字语言转化为数学语言是:
已知:
求证:
∠A=∠B=∠C
△ABC是等边三角形
A
B
C
3、等边三角形的判定方法2:
有一个角是60°的等腰三角形是等边三角形
已知:
求证:
△ABC是等腰三角形,若∠A=60°
△ABC是等边三角形
A
B
C
把这个命题的文字语言转化为数学语言是:
例1 如图,在等边三角形ABC中,DE∥BC, 求证:△ADE是等边三角形.
A
C
B
D
E
典例精析
证明:
∵ △ABC是等边三角形,
∴ ∠A= ∠B= ∠C.
∵ DE//BC,
∴ ∠ADE= ∠B, ∠ AED= ∠C.
∴ ∠A= ∠ADE= ∠ AED.
∴ △ADE是等边三角形.
想一想:本题还有其他证法吗?
变式:上题中,若将条件DE∥BC改为AD=AE, △ADE还是等边三角形吗?试说明理由.
A
C
B
D
E
如图,在等边三角形ABC中,AD=AE, 求证:△ADE是等边三角形.
1、下列四个说法中,不正确的有( )
①三个角都相等的三角形是等边三角形。
②有两个角等于60°的三角形是等边三角形.
③有一个角是60°的等腰三角形是等边三角形.
④有两个角相等的等腰三角形是等边三角形.
④
随堂练习
随堂练习
2、已知△ABC中,∠A=∠B=60°,AB=3cm
则△ABC的周长为________
3、△ABC是等腰三角形,周长为15cm且∠A=60°,
则BC=_______
4、如图,等边三角形ABC中,AD是BC上的高,
∠ BDE=∠CDF=60 °,
图中有哪些与BD相等的线段?
(书P80练习2)
9cm
5cm
BD=AE=BE=CD=CF=AF=DF=DE
B
C
D
A
E
5.如图,等边三角形ABC中,BD是AC边上的中线,BD=BE,求∠EDA的度数.
解:
∵ △ABC是等边三角形,
∴∠CBA=60°.
∵BD是AC边上的中线,
∴∠BDA=90°, ∠DBA=30 °.
∵ BD=BE,
∴ ∠BDE=(180 °- ∠DBA) ÷2 =(180°-30°) ÷2=75°.
∴ ∠EDA=90 °- ∠BDE=90°-75°=15°.
(1)等边三角形的性质:
小结:
1. 等边三角形的三边相等
2. 等边三角形的内角都相等,且都等于60 °
3. 等边三角形各边上中线,高和所对角的平分线都三线合一.
4. 等边三角形是轴对称图形,有三条对称轴
(2) 等边三角形的判定:
1.三边相等的三角形是等边三角形.
2.三个内角都等于60 °的三角形是等边三角形.
3.有一个内角等于60 °的等腰三角形是等边三角形.
学以致用
如图,△ABD,△AEC都是等边三角形。
求证:BE=DC
E
D
C
B
A
