人教版八年级数学上册第14章: 整式的乘法与因式分解全章复习 课件(第一课时 34张)
文档属性
| 名称 | 人教版八年级数学上册第14章: 整式的乘法与因式分解全章复习 课件(第一课时 34张) |  | |
| 格式 | pptx | ||
| 文件大小 | 299.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-19 20:45:01 | ||
图片预览











文档简介
整式的乘法与因式分解
全章复习(第一课时)
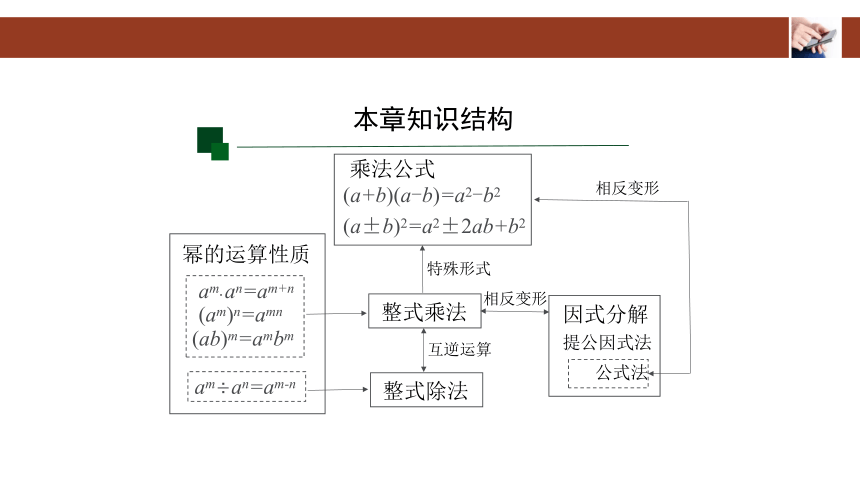
本章知识结构
整式乘法
幂的运算性质
am an=am+n
(am)n=amn
(ab)m=ambm
.
(a+b)(a-b)=a2-b2
(a±b)2=a2±2ab+b2
乘法公式
特殊形式
因式分解
提公因式法
公式法
相反变形
相反变形
互逆运算
整式除法
am÷an=am-n
本章知识结构
整式乘法
幂的运算性质
am an=am+n
(am)n=amn
(ab)m=ambm
.
(a+b)(a-b)=a2-b2
(a±b)2=a2±2ab+b2
乘法公式
特殊形式
互逆运算
整式除法
am÷an=am-n
典例选讲
例 判断下面的计算对不对?如果不对,
应该怎样改正?
(1)a2·a3=a6; (2)(b4)3=b7;
(3)a10÷a2=a5; (4)(-2ab2)3=-8a3b6.
例 判断下面的计算对不对?如果不对,
应该怎样改正?
(1)a2·a3=a6;
同底数幂相乘,底数不变,指数相加.
×
正确:a2·a3=a2+3=a5.
例 判断下面的计算对不对?如果不对,
应该怎样改正?
(2)(b4)3=b7;
×
幂的乘方,底数不变,指数相乘.
正确:(b4)3=b4×3=b12.
例 判断下面的计算对不对?如果不对,
应该怎样改正?
(3)a10÷a2=a5;
×
正确:a10÷a2=a10-2=a8.
同底数幂相除,底数不变,指数相减.
例 判断下面的计算对不对?如果不对,
应该怎样改正?
(4)(-2ab2)3=-8a3b6.
(-2ab2)3=(-2)3a3(b2)3=-8a3b6.
积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘.
√
小结:
1.幂的运算法则:
(1)am·an=am+n(m,n都是正整数);
(2)(am)n=amn(m,n都是正整数);
(3)am÷an=am-n(a≠0,m,n都是正整数,
并且m>n);
(4)(ab)n=anbn(n都是正整数).
2.使用法则时,要明确法则和具体内容.
例 已知10m=5,10n=3,求102m+3n的值.
分析:
am·an=am+n
逆用:am+n=am·an
102m+3n=102m·103n
(am)n=amn
逆用:amn=(am)n
=(an)m
(10m)2
=
(10n)3
=
例 已知10m=5,10n=3,求102m+3n的值.
解:
102m+3n=102m·103n
=(10m)2·(10n)3.
将10m=5,10n=3代入,
原式=52×33=25×27=675.
巩固练习
计算:
(ab)n=anbn
分析:
逆用:anbn=(ab)n
逆用:am+n=am·an
am·an=am+n
解:
小结:
逆用幂的运算法则:
(1)am+n=am·an(m,n都是正整数);
(2)amn=(am)n(m,n都是正整数);
(3)am-n=am÷an(a≠0,m,n都是正整数,
并且m>n);
(4)anbn=(ab)n(n都是正整数).
例 若定义一种新运算,a*b=2ab-b2,
求 x*(x+2y).
两数*运算,等于这两数乘积的2倍与后一个数的平方的差.
例 若定义一种新运算,a*b=2ab-b2,
求 x*(x+2y).
解:
∵ a*b=2ab-b2,
∴ x*(x+2y)
a=x,b=x+2y .
=2x(x+2y)-(x+2y)2
单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加.
单项式与单项式相乘,把它们的系数、同底数幂分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
转化
例 若定义一种新运算,a*b=2ab-b2,
求 x*(x+2y).
解:
∵ a*b=2ab-b2,
∴ x*(x+2y)
a=x,b=x+2y .
=2x(x+2y)-(x+2y)2
=2x2+4xy
-(x2+4xy+4y2)
完全平方公式:(a+b)2=a2+2ab+b2.
=2x2+4xy-x2-4xy-4y2
=x2-4y2.
例 若定义一种新运算,a*b=2ab-b2,
求 x*(x+2y).
解:
∵ a*b=2ab-b2,
∴ x*(x+2y)
a=x,b=x+2y .
=2x(x+2y)-(x+2y)2
=(x+2y)[2x-(x+2y)]
=(x+2y)(2x-x-2y)
=(x+2y)(x-2y)
平方差公式:(a+b)(a-b)=a2-b2.
=x2-4y2.
巩固练习
先化简再求值:
(ab+2)(ab-2)-(a2b2-4ab)÷ab,
其中a=-3,b= .
解:
(ab+2)(ab-2)-(a2b2-4ab)÷ab
=a2b2-4
多项式除以单项式,先把这个多项式的每一项除以这个单项式,再把所得的商相加.
单项式相除,把系数与同底数幂分别相除作为商的因式,对于只在被除式里含有的字母,则连同它的指数作为商的一个因式.
转化
解:
(ab+2)(ab-2)-(a2b2-4ab)÷ab
=a2b2-4
-(ab-4)
=a2b2-4-ab+4
=a2b2-ab.
将a=-3,b= 代入,
原式=(ab)2-ab
= .
解:
(ab+2)(ab-2)-(a2b2-4ab)÷ab
=a2b2-4
-(ab-4)
=a2b2-4-ab+4
=a2b2-ab.
将a=-3,b= 代入,
原式=ab(ab-1)
= .
小结:
1.明确运算顺序:
(1)有括号要先算括号里的;
(2)先乘方,再乘除,最后加减.
2.明确运算法则:
(1)整式的运算法则,单项式的乘除法是关键;
(2)新定义的运算法则,一般转化为学过的
运算法则.
小结:
3.运算中正确使用乘法公式:
平方差公式: (a+b)(a-b)=a2-b2;
完全平方公式:(a±b)2=a2±2ab+b2.
例 如图1是一个长为4b、宽为a的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成一个“回形”正方形(如图2).
(1)观察图2,请写出(a+b)2,(a-b)2,ab之间的数量关系;
图2
a
a
b
b
图1
a
4b
(a+b)2
(a-b)2
ab
解:
(1)
S大
S阴
S长
a-b
=
+ 4
=
+4
图2
a
a
b
b
图1
a
4b
(2)应用:根据(1)中的结论,若x+y=5, ,求x-y的值.
(a+b)2=(a-b)2+4ab
解:
(1)
(2)∵x+y=5, ,
∴
∴
∴
完全平方公式:(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
①
②
①+②,(a+b)2+(a-b)2=2(a2+b2)
①-②,(a+b)2-(a-b)2=4ab
小结:
变形:
a+b,a-b,
ab,a2+b2,
知二求二.
巩固练习
已知长方形ABCD的周长为20,面积为28,求分别以长方形的长和宽为边长的正方形面积之和是多少?
A
B
C
D
x2
y2
x
y
分析:
巩固练习
已知长方形ABCD的周长为20,面积为28,求分别以长方形的长和宽为边长的正方形面积之和是多少?
A
B
C
D
x2
y2
x
y
解:设长方形ABCD的长是x,宽是y,则
∴分别以长方形的长和宽为边长
的正方形面积之和是44.
归纳总结
1.对于运算问题:明确法则,理清顺序;
2.使用运算法则:既可以正用,也可以逆用;
既可以直接用,也可以变形用.
课后作业
1.计算:
(1)(2a)3·b4÷12a3b2; (2)(2a+3b)(2a-b);
(3)3(y-z)2-(2y+z)(-z+2y);
(4)[x(x2y2-xy)-y(x2-x3y)]÷3x2y.
2.求证:当n是整数时,两个连续奇数的平方差
(2n+1)2-(2n-1)2是8的倍数.
同学们,再见!
全章复习(第一课时)
本章知识结构
整式乘法
幂的运算性质
am an=am+n
(am)n=amn
(ab)m=ambm
.
(a+b)(a-b)=a2-b2
(a±b)2=a2±2ab+b2
乘法公式
特殊形式
因式分解
提公因式法
公式法
相反变形
相反变形
互逆运算
整式除法
am÷an=am-n
本章知识结构
整式乘法
幂的运算性质
am an=am+n
(am)n=amn
(ab)m=ambm
.
(a+b)(a-b)=a2-b2
(a±b)2=a2±2ab+b2
乘法公式
特殊形式
互逆运算
整式除法
am÷an=am-n
典例选讲
例 判断下面的计算对不对?如果不对,
应该怎样改正?
(1)a2·a3=a6; (2)(b4)3=b7;
(3)a10÷a2=a5; (4)(-2ab2)3=-8a3b6.
例 判断下面的计算对不对?如果不对,
应该怎样改正?
(1)a2·a3=a6;
同底数幂相乘,底数不变,指数相加.
×
正确:a2·a3=a2+3=a5.
例 判断下面的计算对不对?如果不对,
应该怎样改正?
(2)(b4)3=b7;
×
幂的乘方,底数不变,指数相乘.
正确:(b4)3=b4×3=b12.
例 判断下面的计算对不对?如果不对,
应该怎样改正?
(3)a10÷a2=a5;
×
正确:a10÷a2=a10-2=a8.
同底数幂相除,底数不变,指数相减.
例 判断下面的计算对不对?如果不对,
应该怎样改正?
(4)(-2ab2)3=-8a3b6.
(-2ab2)3=(-2)3a3(b2)3=-8a3b6.
积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘.
√
小结:
1.幂的运算法则:
(1)am·an=am+n(m,n都是正整数);
(2)(am)n=amn(m,n都是正整数);
(3)am÷an=am-n(a≠0,m,n都是正整数,
并且m>n);
(4)(ab)n=anbn(n都是正整数).
2.使用法则时,要明确法则和具体内容.
例 已知10m=5,10n=3,求102m+3n的值.
分析:
am·an=am+n
逆用:am+n=am·an
102m+3n=102m·103n
(am)n=amn
逆用:amn=(am)n
=(an)m
(10m)2
=
(10n)3
=
例 已知10m=5,10n=3,求102m+3n的值.
解:
102m+3n=102m·103n
=(10m)2·(10n)3.
将10m=5,10n=3代入,
原式=52×33=25×27=675.
巩固练习
计算:
(ab)n=anbn
分析:
逆用:anbn=(ab)n
逆用:am+n=am·an
am·an=am+n
解:
小结:
逆用幂的运算法则:
(1)am+n=am·an(m,n都是正整数);
(2)amn=(am)n(m,n都是正整数);
(3)am-n=am÷an(a≠0,m,n都是正整数,
并且m>n);
(4)anbn=(ab)n(n都是正整数).
例 若定义一种新运算,a*b=2ab-b2,
求 x*(x+2y).
两数*运算,等于这两数乘积的2倍与后一个数的平方的差.
例 若定义一种新运算,a*b=2ab-b2,
求 x*(x+2y).
解:
∵ a*b=2ab-b2,
∴ x*(x+2y)
a=x,b=x+2y .
=2x(x+2y)-(x+2y)2
单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加.
单项式与单项式相乘,把它们的系数、同底数幂分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
转化
例 若定义一种新运算,a*b=2ab-b2,
求 x*(x+2y).
解:
∵ a*b=2ab-b2,
∴ x*(x+2y)
a=x,b=x+2y .
=2x(x+2y)-(x+2y)2
=2x2+4xy
-(x2+4xy+4y2)
完全平方公式:(a+b)2=a2+2ab+b2.
=2x2+4xy-x2-4xy-4y2
=x2-4y2.
例 若定义一种新运算,a*b=2ab-b2,
求 x*(x+2y).
解:
∵ a*b=2ab-b2,
∴ x*(x+2y)
a=x,b=x+2y .
=2x(x+2y)-(x+2y)2
=(x+2y)[2x-(x+2y)]
=(x+2y)(2x-x-2y)
=(x+2y)(x-2y)
平方差公式:(a+b)(a-b)=a2-b2.
=x2-4y2.
巩固练习
先化简再求值:
(ab+2)(ab-2)-(a2b2-4ab)÷ab,
其中a=-3,b= .
解:
(ab+2)(ab-2)-(a2b2-4ab)÷ab
=a2b2-4
多项式除以单项式,先把这个多项式的每一项除以这个单项式,再把所得的商相加.
单项式相除,把系数与同底数幂分别相除作为商的因式,对于只在被除式里含有的字母,则连同它的指数作为商的一个因式.
转化
解:
(ab+2)(ab-2)-(a2b2-4ab)÷ab
=a2b2-4
-(ab-4)
=a2b2-4-ab+4
=a2b2-ab.
将a=-3,b= 代入,
原式=(ab)2-ab
= .
解:
(ab+2)(ab-2)-(a2b2-4ab)÷ab
=a2b2-4
-(ab-4)
=a2b2-4-ab+4
=a2b2-ab.
将a=-3,b= 代入,
原式=ab(ab-1)
= .
小结:
1.明确运算顺序:
(1)有括号要先算括号里的;
(2)先乘方,再乘除,最后加减.
2.明确运算法则:
(1)整式的运算法则,单项式的乘除法是关键;
(2)新定义的运算法则,一般转化为学过的
运算法则.
小结:
3.运算中正确使用乘法公式:
平方差公式: (a+b)(a-b)=a2-b2;
完全平方公式:(a±b)2=a2±2ab+b2.
例 如图1是一个长为4b、宽为a的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成一个“回形”正方形(如图2).
(1)观察图2,请写出(a+b)2,(a-b)2,ab之间的数量关系;
图2
a
a
b
b
图1
a
4b
(a+b)2
(a-b)2
ab
解:
(1)
S大
S阴
S长
a-b
=
+ 4
=
+4
图2
a
a
b
b
图1
a
4b
(2)应用:根据(1)中的结论,若x+y=5, ,求x-y的值.
(a+b)2=(a-b)2+4ab
解:
(1)
(2)∵x+y=5, ,
∴
∴
∴
完全平方公式:(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
①
②
①+②,(a+b)2+(a-b)2=2(a2+b2)
①-②,(a+b)2-(a-b)2=4ab
小结:
变形:
a+b,a-b,
ab,a2+b2,
知二求二.
巩固练习
已知长方形ABCD的周长为20,面积为28,求分别以长方形的长和宽为边长的正方形面积之和是多少?
A
B
C
D
x2
y2
x
y
分析:
巩固练习
已知长方形ABCD的周长为20,面积为28,求分别以长方形的长和宽为边长的正方形面积之和是多少?
A
B
C
D
x2
y2
x
y
解:设长方形ABCD的长是x,宽是y,则
∴分别以长方形的长和宽为边长
的正方形面积之和是44.
归纳总结
1.对于运算问题:明确法则,理清顺序;
2.使用运算法则:既可以正用,也可以逆用;
既可以直接用,也可以变形用.
课后作业
1.计算:
(1)(2a)3·b4÷12a3b2; (2)(2a+3b)(2a-b);
(3)3(y-z)2-(2y+z)(-z+2y);
(4)[x(x2y2-xy)-y(x2-x3y)]÷3x2y.
2.求证:当n是整数时,两个连续奇数的平方差
(2n+1)2-(2n-1)2是8的倍数.
同学们,再见!
