人教版八年级数学下册 18.1.2 平行四边形判定 第三课时 三角形的中位线课件(24张)
文档属性
| 名称 | 人教版八年级数学下册 18.1.2 平行四边形判定 第三课时 三角形的中位线课件(24张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 242.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-19 00:00:00 | ||
图片预览






文档简介
18.1.2 平行四边形判定
第十八章 平行四边形
第3课时 三角形的中位线
我们在研究平行四边形时,经常采用把平行四边形转化为三角形的问题,反过来,能否用平行四边形研究三角形呢?
学习目标
1.知道什么是三角形的中位线.
2.知道三角形中位线的性质.
一、新课引入
1、平行四边形的判定定理:
①两组对边分别___的四边形是平行四边形;
②两组对边分___的四边形是平行四边形;
③两组对角分别___的四边形是平行四边形;
④对角线______的四边形是平行四边形;
⑤一组对边_____的四边形是平行四边形.
平行
相等
相等
互相平分
平行且相等
A
B
C
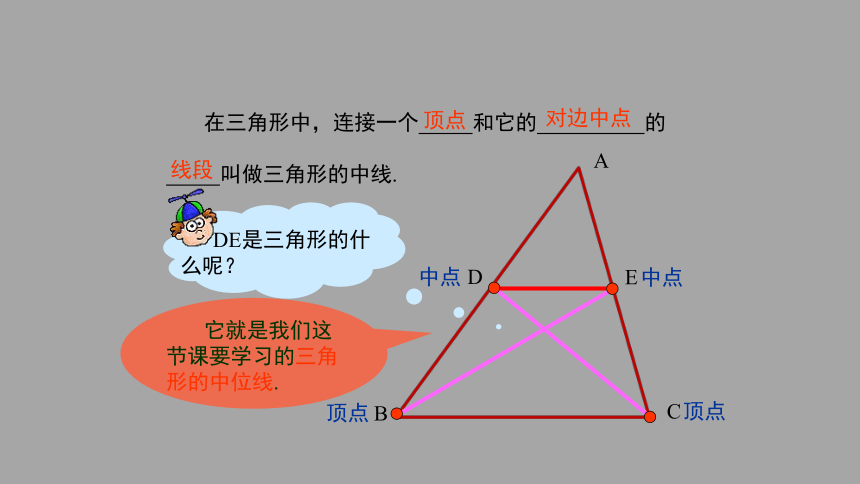
在三角形中,连接一个 和它的 的
叫做三角形的中线.
顶点
顶点
D
中点
DE是三角形的什么呢?
E
中点
它就是我们这节课要学习的三角形的中位线.
顶点
对边中点
线段
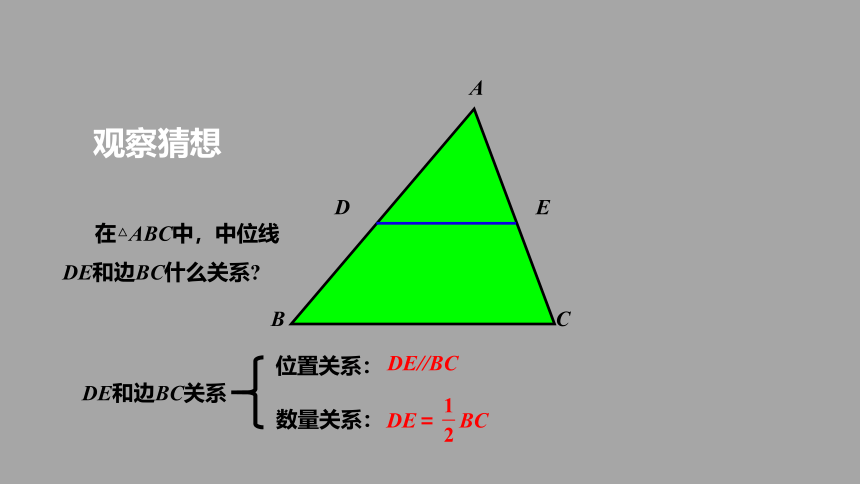
DE和边BC关系
DE//BC
DE= BC
观察猜想
在△ABC中,中位线DE和边BC什么关系?
A
B
C
D
E
数量关系:
位置关系:
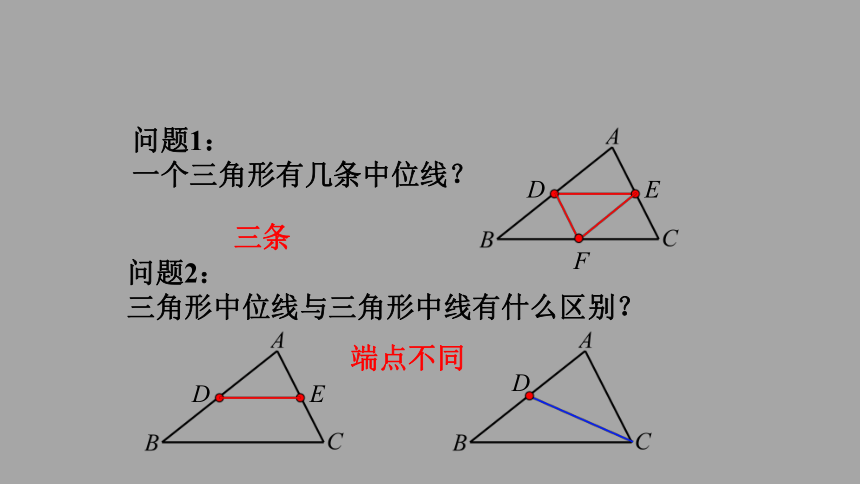
问题1:
一个三角形有几条中位线?
D
E
F
三条
问题2:
三角形中位线与三角形中线有什么区别?
D
E
D
端点不同
度量一下你手中的三角形,看看是否有同样的结论?并用文字表述这一结论.
如图,DE是△ABC的中位线,
DE与BC有怎样的关系?
D
E
如图,点D、E、分别为△ABC的边AB、
AC的中点.求证:DE∥BC且DE= BC.
证明:如图,延长DE到点F,使EF=DE,连接
CF、CD和AF,∵AE= ,DE= ,
∴四边形ADCF是平行四边(对角线互相平分
的四边形是平行四边形)
∴CF_DA ,
又∵AD=BD
∴CF _ ,
∴四边形DBCF是平行四边形.
∴DF _BC ,
又∵DE= DF,
∴ ∥ 且DE= BC
温馨提示: “_”表示平行且相等
A
B
C
D
E
F
∥
∥
∥
∥
AC
EF
BD
DE
BC
三角形的中位线定理:
三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
三角形的中位线平行于三角形的第三边且等于第三边的一半.
D
E
△ABC中,若D、E分别是边AB、AC的中点,
则DE∥BC,DE= BC.
符号语言:
如图,在△ABC中,D,E,F分别是AB,AC,BC的中点,以这些点为顶点,在图中,你能画出多少个平行四边形?为什么?
例 如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA中点.
求证:四边形EFGH是平行四边形.
四边形问题
连接对角线
三角形问题
(三角形中位线定理)
例 如图所示,D是△ABC内一点,BD⊥CD,AD=6,
BD=4,CD=3,E、F、G、H分别是AB、AC、CD、
BD的中点,则四边形EFGH的周长是 .
利用勾股定理列式求出BC的长,
再根据三角形的中位线平行于第
三边并且等于第三边的一半求出
EH=FG = AD,
EF=GH = BC,然后代入数据
进行计算即可得解.
11
1. 如图,△ABC中,D、E分别是AB、AC中点.
(1) 若DE=5,则BC= .
(2) 若∠B=65°,则∠ADE= °.
(3) 若DE+BC=12,则BC= .
10
65
x
2x
x+2x=12
x=4
8
2.如图,A,B两点被池塘隔开,在AB外选一点C,连接AC,BC.怎样测出A,B两点间的距离?根据是什么?
随堂演练
1.如图,点D,E,F分别是△ABC三边的中点,若AB=10cm,AC=8cm,BC=12cm,则EF=____,DF=____,DE=____,△DEF的周长为______ .
5cm
4cm
6cm
15cm
2、已知:△ABC中,点D、E、F分别是△ABC三边的中点,如果△DEF的周长是12cm,那么△ABC的周长是?? ?? cm.
3、一个三角形的周长是135cm,过三角形各顶点作对边的平行线,则这三条平行线所组成的三角形的周长是?? ?cm.
6
270
4.如图,?ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,求△DOE的周长.
解:∵?ABCD的周长为36,
∴BC+CD=18.
∵点E是CD的中点,
∴OE是△BCD的中位线,DE= CD,
∴OE= BC,
∴△DOE的周长为OD+OE+DE=
(BD+BC+CD)=15,
即△DOE的周长为15.
5.如图,在?ABCD中,对角线AC,BD相交于点O,点E是AB的中点,OE=5 cm,则AD的长为______cm.
10
4.已知:如图,点D,E,F分别是△ABC三边上的中点.求证:AD与EF互相平分.
(提示:连接ED,FD,先证四边形AEDF是平行四边形)
知识总结:三角形中位线概念;
三角形中位线定理.
三角形的中位线平行于三角形的第三边,且等于第三边的一半.
通过今天的学习,
能说说你的收获和体会吗?
你有什么经验与收获让同学们共享呢?
第十八章 平行四边形
第3课时 三角形的中位线
我们在研究平行四边形时,经常采用把平行四边形转化为三角形的问题,反过来,能否用平行四边形研究三角形呢?
学习目标
1.知道什么是三角形的中位线.
2.知道三角形中位线的性质.
一、新课引入
1、平行四边形的判定定理:
①两组对边分别___的四边形是平行四边形;
②两组对边分___的四边形是平行四边形;
③两组对角分别___的四边形是平行四边形;
④对角线______的四边形是平行四边形;
⑤一组对边_____的四边形是平行四边形.
平行
相等
相等
互相平分
平行且相等
A
B
C
在三角形中,连接一个 和它的 的
叫做三角形的中线.
顶点
顶点
D
中点
DE是三角形的什么呢?
E
中点
它就是我们这节课要学习的三角形的中位线.
顶点
对边中点
线段
DE和边BC关系
DE//BC
DE= BC
观察猜想
在△ABC中,中位线DE和边BC什么关系?
A
B
C
D
E
数量关系:
位置关系:
问题1:
一个三角形有几条中位线?
D
E
F
三条
问题2:
三角形中位线与三角形中线有什么区别?
D
E
D
端点不同
度量一下你手中的三角形,看看是否有同样的结论?并用文字表述这一结论.
如图,DE是△ABC的中位线,
DE与BC有怎样的关系?
D
E
如图,点D、E、分别为△ABC的边AB、
AC的中点.求证:DE∥BC且DE= BC.
证明:如图,延长DE到点F,使EF=DE,连接
CF、CD和AF,∵AE= ,DE= ,
∴四边形ADCF是平行四边(对角线互相平分
的四边形是平行四边形)
∴CF_DA ,
又∵AD=BD
∴CF _ ,
∴四边形DBCF是平行四边形.
∴DF _BC ,
又∵DE= DF,
∴ ∥ 且DE= BC
温馨提示: “_”表示平行且相等
A
B
C
D
E
F
∥
∥
∥
∥
AC
EF
BD
DE
BC
三角形的中位线定理:
三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
三角形的中位线平行于三角形的第三边且等于第三边的一半.
D
E
△ABC中,若D、E分别是边AB、AC的中点,
则DE∥BC,DE= BC.
符号语言:
如图,在△ABC中,D,E,F分别是AB,AC,BC的中点,以这些点为顶点,在图中,你能画出多少个平行四边形?为什么?
例 如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA中点.
求证:四边形EFGH是平行四边形.
四边形问题
连接对角线
三角形问题
(三角形中位线定理)
例 如图所示,D是△ABC内一点,BD⊥CD,AD=6,
BD=4,CD=3,E、F、G、H分别是AB、AC、CD、
BD的中点,则四边形EFGH的周长是 .
利用勾股定理列式求出BC的长,
再根据三角形的中位线平行于第
三边并且等于第三边的一半求出
EH=FG = AD,
EF=GH = BC,然后代入数据
进行计算即可得解.
11
1. 如图,△ABC中,D、E分别是AB、AC中点.
(1) 若DE=5,则BC= .
(2) 若∠B=65°,则∠ADE= °.
(3) 若DE+BC=12,则BC= .
10
65
x
2x
x+2x=12
x=4
8
2.如图,A,B两点被池塘隔开,在AB外选一点C,连接AC,BC.怎样测出A,B两点间的距离?根据是什么?
随堂演练
1.如图,点D,E,F分别是△ABC三边的中点,若AB=10cm,AC=8cm,BC=12cm,则EF=____,DF=____,DE=____,△DEF的周长为______ .
5cm
4cm
6cm
15cm
2、已知:△ABC中,点D、E、F分别是△ABC三边的中点,如果△DEF的周长是12cm,那么△ABC的周长是?? ?? cm.
3、一个三角形的周长是135cm,过三角形各顶点作对边的平行线,则这三条平行线所组成的三角形的周长是?? ?cm.
6
270
4.如图,?ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,求△DOE的周长.
解:∵?ABCD的周长为36,
∴BC+CD=18.
∵点E是CD的中点,
∴OE是△BCD的中位线,DE= CD,
∴OE= BC,
∴△DOE的周长为OD+OE+DE=
(BD+BC+CD)=15,
即△DOE的周长为15.
5.如图,在?ABCD中,对角线AC,BD相交于点O,点E是AB的中点,OE=5 cm,则AD的长为______cm.
10
4.已知:如图,点D,E,F分别是△ABC三边上的中点.求证:AD与EF互相平分.
(提示:连接ED,FD,先证四边形AEDF是平行四边形)
知识总结:三角形中位线概念;
三角形中位线定理.
三角形的中位线平行于三角形的第三边,且等于第三边的一半.
通过今天的学习,
能说说你的收获和体会吗?
你有什么经验与收获让同学们共享呢?
