湘教版数学九年级下第一章《反比例函数》单元测试题及答案
文档属性
| 名称 | 湘教版数学九年级下第一章《反比例函数》单元测试题及答案 |  | |
| 格式 | zip | ||
| 文件大小 | 256.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-02 15:48:06 | ||
图片预览



文档简介
《反比例函数》水平测试题
(满分:120分 时间:90分钟)
一、选择题(每题3分,共30分)
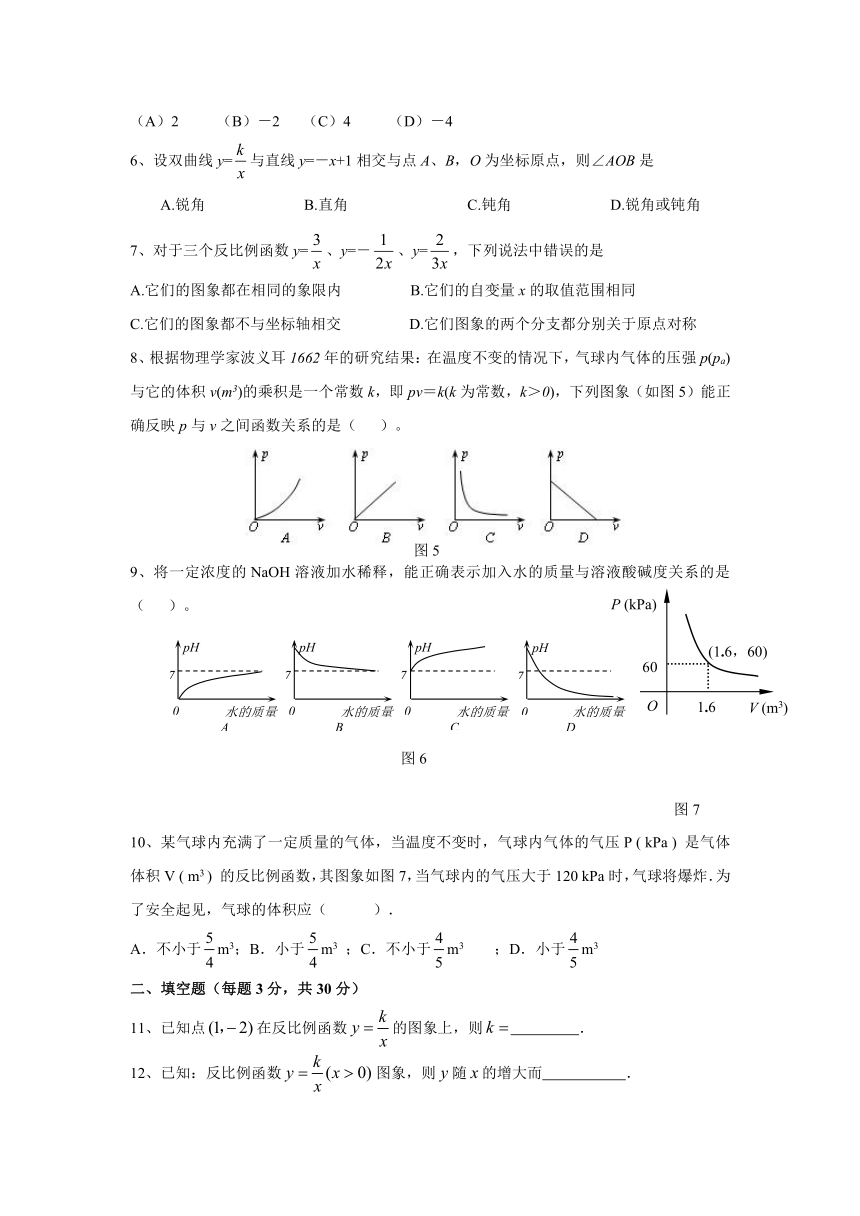
1、函数与在同一坐标系内的图象可以是( )
2、如图2在矩形ABCD中,AB=3,BC=4,点P在BC边上运动,连结DP,过点A作AE⊥DP,垂足为E,设DP=,AE=,则能反映与之间函数关系的大致图象是( )
(A) (B) (C) (D)
3、一张正方形的纸片,剪去两个一样的小矩形得到一个“E”图案,如图3所示,设小矩形的长和宽分别为x、y,剪去部分的面积为20,若2≤x≤10,则y与x的函数图象是( )
4、函数的图象上有两点,,若0<,则( )A. B. C. D.、的大小不确定
5、反比例函数的图象如图4示,点M是该函数图象上一点,
MN垂直于x轴,垂足是点N,如果=2,则k的值为( )
(A)2 (B)-2 (C)4 (D)-4
6、设双曲线y=与直线y=-x+1相交与点A、B,O为坐标原点,则∠AOB是
A.锐角 B.直角 C.钝角 D.锐角或钝角
7、对于三个反比例函数y=、y=-、y=,下列说法中错误的是
A.它们的图象都在相同的象限内 B.它们的自变量x的取值范围相同
C.它们的图象都不与坐标轴相交 D.它们图象的两个分支都分别关于原点对称
8、根据物理学家波义耳1662年的研究结果:在温度不变的情况下,气球内气体的压强p(pa)与它的体积v(m3)的乘积是一个常数k,即pv=k(k为常数,k>0),下列图象(如图5)能正确反映p与v之间函数关系的是( )。
9、将一定浓度的NaOH溶液加水稀释,能正确表示加入水的质量与溶液酸碱度关系的是( )。
10、某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P ( kPa ) 是气体体积V ( m3 ) 的反比例函数,其图象如图7,当气球内的气压大于120 kPa时,气球将爆炸.为了安全起见,气球的体积应( ).
A.不小于m3;B.小于m3 ;C.不小于m3 ;D.小于m3
二、填空题(每题3分,共30分)
11、已知点在反比例函数的图象上,则 .
12、已知:反比例函数图象,则随的增大而 .
13、在对物体做功一定的情况下,力F(牛)与此物体在力的方向上移动的距离s(米)成反比例函数关系,其图象如图8示,P(5,1)在图象上,则当力达到10牛时,物体在力的方向上移动的距离是 米.
14、如图9,已知反比例函数的图像上有一点P,过点P分别作x轴和y轴的垂线,垂足分别为A、B,使四边形OAPB为正方形。又在反比例函数的图像上有一点P1,过点P1分别作BP和y轴的垂线,垂足分别为A1、B1,使四边形BA1P1B1为正方形,则点P1的坐标是 。
15、写出具有性质“图象的两个分支分别在第二、四象限内,且在每一个象限内,y随x的增大而增大”的一个反比例函数_____________.
16、平面直角坐标系中有六个点,,,,,,其中有五个点在同一反比例函数图象上,不在这个反比例函数图象上的点
是
17、某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P ( kPa ) 是气体体积V ( m3 ) 的反比例函数,其图象如图10.当气球内的气压大于120 kPa时,气球将爆炸.为了安全起见,气球的体积应 .
18、若反比例函数的图象上有两点,,则______(填“”或“”或“”).
19、如图11,已知双曲线(x>0)经过矩形OABC边AB的中点F,交BC于点E,且四边形OEBF的面积为2,则k=______________。
20、如图12,直线与双曲线交于点.过点作轴,垂足为点,连结.若,则的值是
三、解答题(共60分)
21.(本题6分)已知反比例函数y=与第三象限的角平分线交于点P,且P点到原点的距离等于4,求函数的解析式.
22.(本题6分)如图13,△ABC是边长为2的等边三角形,点E、F分别
在CB和BC的延长线上,且∠EAF=120°,设BE=x,CF=y.
求y与x的函数关系,并画出这个函数的图象.
23.(本题7分)已知正比例函数y=x与反比例函数y=(x>0)相交于点A,而反比例函数y=(x>0)又与一次函数y=4-x相交于点B和C.
(1)求A、B、C的坐标.
(2)求△ABC的面积.
24.(本题7分)如图14,一次函数的图象与反比例函数的图象交于两点.
(1)试确定上述反比例函数和一次函数的表达式;
(2)求的面积.
25.(本题8分)已知:A(-4,2)、B(n,-4)是一次函数y=kx+b的图象与反比例函数的图象的两个交点.
(1) 求此反比例函数和一次函数的解析式;
(2) 根据图象写出使一次函数的值小于反比例函数的值的x的取值范围.
26.(本题8分)(1)已知矩形A的长、宽分别是2和1,那么是否存在另一个矩形B,它的周长和面积分别是矩形A的周长和面积的2倍?对上述问题,小明同学从“图形”的角度,利用函数图象给予了解决。小明论证的过程开始是这样的:如果用x、y分别表示矩形的长和宽,那么矩形B满足x+y=6,xy=4。请你按照小明的论证思路完成后面的论证过程。
(2)已知矩形A的长和宽分别是2和1,那么是否存在一个矩形C,它的周长和面积分别是矩形A的周长和面积的一半?小明认为这个问题是肯定的,你同意小明的观点吗?为什么?
27.(本题9分)2008义乌市经济继续保持平稳较快的增长态势,全市实现生产总值元,已知全市生产总值=全市户籍人口×全市人均生产产值,设义乌市2008年户籍人口为x(人),人均生产产值为y(元).
(1)求y关于x的函数关系式;
(2)2008年义乌市户籍人口为706 684人,求2008年义乌市人均生产产值(单位:元,结果精确到个位):若按2008年全年美元对人民币的平均汇率计(1美元=7.96元人民币),义乌市2008年人均生产产值是否已跨越6000美元大关?
28.(本题9分)如图16,已知直线与双曲线交于两点,且点的横坐标为.(1)求的值;
(2)若双曲线上一点的纵坐标为8,求的面积;
(3)过原点的另一条直线交双曲线于两点(点在第一象限),若由点为顶点组成的四边形面积为,求点的坐标.
参考答案:
一、1、C;2、C;3、A;4、A;5、B;6、D;7、A ;8、C;9、B;10、C;
二、11、-2; 12、减小;13、0.5;14、;15、如:y=-;
16、点D; 17、小于m3;18、;19、2;20、1;
三、21、∵y=与第三象限的角平分线交于P点,设P点为(a,a),则a2+a2=42,a2=8,
而点P(a,a)在y=上,∴k=8,∴y=.
22、由△ABE∽△FCA,得函数式y=.
23、(1)由,得x1=1,x2=-1(舍去),当x=1时,y=1,∴A(1,1)
由得,,
∴C(2+,2-),B(2-,2+)
(2)过B、A、C三点向x轴作垂线,垂足为B′、A′、C′.BB′=2+,AA′=1,CC′=2-,B′C′=2,B′A′=-1,A′C′=+1
S△ABC=S梯形BB′C′C-S梯形BB′A′A-S梯形AA′C′C=2.
24.解:(1)点在反比例函数的图象上,
.
反比例函数的表达式为.
点也在反比例函数的图象上,
,即.
把点,点代入一次函数中,得
解得一次函数的表达式为.
(2)在中,当时,得.直线与轴的交点为.
线段将分成和,
.
25.(1) ∵ 点A(-4,2)和点B(n,-4)都在反比例函数y=的图象上,
∴ 解得
又由点A(-4,2)和点B(2,-4)都在一次函数y=kx+b的图象上,
∴ 解得
∴ 反比例函数的解析式为,一次函数的解析式为y=-x-2 .
(2) x的取值范围是x>2或-4<x<0 .
26.解:(1)可以看作一次函数的图象在第一象限内点的坐标,又可以看作反比例函数的图象在第一象限内点的坐标,而满足问题要求的就可以看作一次函数的图象与反比例函数的图象在第一象限内交点的坐标.
分别画出两图象(图略),从图中可看出,这样的交点存在,即满足要求的矩形存在.
(2)不同意小明的观点.
如果用分别表示矩形的长和宽,那么矩形满足,,而满足要求的可以看作一次函数的图象与反比例函数的图象在第一象限内交点的坐标.
画图(图略)可看出,这样的交点不存在,即满足要求的矩形是不存在的.
所以不同意小明的观点.
27、解:(1)(x为正整数).(x范围不写不扣分)
(2)2006年全市人均生产产值=(元)
∵,∴我市2006年人均生产产值已成功跨越6000美元大关
28、解:(1)∵点A横坐标为4 , ∴当 = 4时, = 2 .∴ 点A的坐标为( 4,2 ).
∵ 点A是直线 与双曲线 (k>0)的交点 ,∴ k = 4 ×2 = 8 .
(2) 解法一:如图12-1,∵ 点C在双曲线上,当 = 8时, = 1∴ 点C的坐标为 ( 1, 8 ) . 过点A、C分别做轴、轴的垂线,垂足为M、N,得矩形DMON .
S矩形ONDM= 32 , S△ONC = 4 , S△CDA = 9, S△OAM = 4 .
S△AOC= S矩形ONDM - S△ONC - S△CDA - S△OAM = 32 - 4 - 9 - 4 = 15 .
解法二:如图12-2,
过点 C、A分别做轴的垂线,垂足为E、F,
∵ 点C在双曲线上,当 = 8时, = 1 .
∴ 点C的坐标为 ( 1, 8 ). ∵ 点C、A都在双曲线上 ,
∴ S△COE = S△AOF = 4 ,∴ S△COE + S梯形CEFA = S△COA + S△AOF .
∴ S△COA = S梯形CEFA ,∵ S梯形CEFA = ×(2+8)×3 = 15 , ∴ S△COA = 15 .
(3)∵ 反比例函数图象是关于原点O的中心对称图形 ,
∴ OP=OQ,OA=OB .
∴ 四边形APBQ是平行四边形 .
∴ S△POA = S平行四边形APBQ = ×24 = 6 .
设点P的横坐标为( > 0且),
得P ( , ) .
过点P、A分别做轴的垂线,垂足为E、F,
∵ 点P、A在双曲线上,∴S△POE = S△AOF = 4 .
若0<<4,如图12-3,
∵ S△POE + S梯形PEFA = S△POA + S△AOF,
∴ S梯形PEFA = S△POA = 6 .
∴ .
解得= 2,= - 8(舍去) ,∴ P(2,4). 若 > 4,如图12-4,
∵ S△AOF+ S梯形AFEP = S△AOP + S△POE,∴ S梯形PEFA = S△POA = 6 . ∴,
解得 = 8, = - 2 (舍去) ,∴ P(8,1).
∴ 点P的坐标是P(2,4)或P(8,1).
图1
图2
图3
M
O
y
x
N
图4
图5
1.6
60
O
V (m3)
P (kPa)
(1.6,60)
pH
0
7
水的质量
pH
0
7
水的质量
pH
0
7
水的质量
A
B
C
D
水的质量
pH
0
7
图6
图7
图12
A
B
C
E
O
F
x
y
图11
图10
图9
图8
图13
O
y
x
B
A
图14
图8
O
x
y
2
4
6
8
2
4
6
8
图15(1)
O
x
y
1
2
3
4
1
2
3
4
图15(2)
图16
O
y
x
B
A
C
图13
(满分:120分 时间:90分钟)
一、选择题(每题3分,共30分)
1、函数与在同一坐标系内的图象可以是( )
2、如图2在矩形ABCD中,AB=3,BC=4,点P在BC边上运动,连结DP,过点A作AE⊥DP,垂足为E,设DP=,AE=,则能反映与之间函数关系的大致图象是( )
(A) (B) (C) (D)
3、一张正方形的纸片,剪去两个一样的小矩形得到一个“E”图案,如图3所示,设小矩形的长和宽分别为x、y,剪去部分的面积为20,若2≤x≤10,则y与x的函数图象是( )
4、函数的图象上有两点,,若0<,则( )A. B. C. D.、的大小不确定
5、反比例函数的图象如图4示,点M是该函数图象上一点,
MN垂直于x轴,垂足是点N,如果=2,则k的值为( )
(A)2 (B)-2 (C)4 (D)-4
6、设双曲线y=与直线y=-x+1相交与点A、B,O为坐标原点,则∠AOB是
A.锐角 B.直角 C.钝角 D.锐角或钝角
7、对于三个反比例函数y=、y=-、y=,下列说法中错误的是
A.它们的图象都在相同的象限内 B.它们的自变量x的取值范围相同
C.它们的图象都不与坐标轴相交 D.它们图象的两个分支都分别关于原点对称
8、根据物理学家波义耳1662年的研究结果:在温度不变的情况下,气球内气体的压强p(pa)与它的体积v(m3)的乘积是一个常数k,即pv=k(k为常数,k>0),下列图象(如图5)能正确反映p与v之间函数关系的是( )。
9、将一定浓度的NaOH溶液加水稀释,能正确表示加入水的质量与溶液酸碱度关系的是( )。
10、某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P ( kPa ) 是气体体积V ( m3 ) 的反比例函数,其图象如图7,当气球内的气压大于120 kPa时,气球将爆炸.为了安全起见,气球的体积应( ).
A.不小于m3;B.小于m3 ;C.不小于m3 ;D.小于m3
二、填空题(每题3分,共30分)
11、已知点在反比例函数的图象上,则 .
12、已知:反比例函数图象,则随的增大而 .
13、在对物体做功一定的情况下,力F(牛)与此物体在力的方向上移动的距离s(米)成反比例函数关系,其图象如图8示,P(5,1)在图象上,则当力达到10牛时,物体在力的方向上移动的距离是 米.
14、如图9,已知反比例函数的图像上有一点P,过点P分别作x轴和y轴的垂线,垂足分别为A、B,使四边形OAPB为正方形。又在反比例函数的图像上有一点P1,过点P1分别作BP和y轴的垂线,垂足分别为A1、B1,使四边形BA1P1B1为正方形,则点P1的坐标是 。
15、写出具有性质“图象的两个分支分别在第二、四象限内,且在每一个象限内,y随x的增大而增大”的一个反比例函数_____________.
16、平面直角坐标系中有六个点,,,,,,其中有五个点在同一反比例函数图象上,不在这个反比例函数图象上的点
是
17、某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P ( kPa ) 是气体体积V ( m3 ) 的反比例函数,其图象如图10.当气球内的气压大于120 kPa时,气球将爆炸.为了安全起见,气球的体积应 .
18、若反比例函数的图象上有两点,,则______(填“”或“”或“”).
19、如图11,已知双曲线(x>0)经过矩形OABC边AB的中点F,交BC于点E,且四边形OEBF的面积为2,则k=______________。
20、如图12,直线与双曲线交于点.过点作轴,垂足为点,连结.若,则的值是
三、解答题(共60分)
21.(本题6分)已知反比例函数y=与第三象限的角平分线交于点P,且P点到原点的距离等于4,求函数的解析式.
22.(本题6分)如图13,△ABC是边长为2的等边三角形,点E、F分别
在CB和BC的延长线上,且∠EAF=120°,设BE=x,CF=y.
求y与x的函数关系,并画出这个函数的图象.
23.(本题7分)已知正比例函数y=x与反比例函数y=(x>0)相交于点A,而反比例函数y=(x>0)又与一次函数y=4-x相交于点B和C.
(1)求A、B、C的坐标.
(2)求△ABC的面积.
24.(本题7分)如图14,一次函数的图象与反比例函数的图象交于两点.
(1)试确定上述反比例函数和一次函数的表达式;
(2)求的面积.
25.(本题8分)已知:A(-4,2)、B(n,-4)是一次函数y=kx+b的图象与反比例函数的图象的两个交点.
(1) 求此反比例函数和一次函数的解析式;
(2) 根据图象写出使一次函数的值小于反比例函数的值的x的取值范围.
26.(本题8分)(1)已知矩形A的长、宽分别是2和1,那么是否存在另一个矩形B,它的周长和面积分别是矩形A的周长和面积的2倍?对上述问题,小明同学从“图形”的角度,利用函数图象给予了解决。小明论证的过程开始是这样的:如果用x、y分别表示矩形的长和宽,那么矩形B满足x+y=6,xy=4。请你按照小明的论证思路完成后面的论证过程。
(2)已知矩形A的长和宽分别是2和1,那么是否存在一个矩形C,它的周长和面积分别是矩形A的周长和面积的一半?小明认为这个问题是肯定的,你同意小明的观点吗?为什么?
27.(本题9分)2008义乌市经济继续保持平稳较快的增长态势,全市实现生产总值元,已知全市生产总值=全市户籍人口×全市人均生产产值,设义乌市2008年户籍人口为x(人),人均生产产值为y(元).
(1)求y关于x的函数关系式;
(2)2008年义乌市户籍人口为706 684人,求2008年义乌市人均生产产值(单位:元,结果精确到个位):若按2008年全年美元对人民币的平均汇率计(1美元=7.96元人民币),义乌市2008年人均生产产值是否已跨越6000美元大关?
28.(本题9分)如图16,已知直线与双曲线交于两点,且点的横坐标为.(1)求的值;
(2)若双曲线上一点的纵坐标为8,求的面积;
(3)过原点的另一条直线交双曲线于两点(点在第一象限),若由点为顶点组成的四边形面积为,求点的坐标.
参考答案:
一、1、C;2、C;3、A;4、A;5、B;6、D;7、A ;8、C;9、B;10、C;
二、11、-2; 12、减小;13、0.5;14、;15、如:y=-;
16、点D; 17、小于m3;18、;19、2;20、1;
三、21、∵y=与第三象限的角平分线交于P点,设P点为(a,a),则a2+a2=42,a2=8,
而点P(a,a)在y=上,∴k=8,∴y=.
22、由△ABE∽△FCA,得函数式y=.
23、(1)由,得x1=1,x2=-1(舍去),当x=1时,y=1,∴A(1,1)
由得,,
∴C(2+,2-),B(2-,2+)
(2)过B、A、C三点向x轴作垂线,垂足为B′、A′、C′.BB′=2+,AA′=1,CC′=2-,B′C′=2,B′A′=-1,A′C′=+1
S△ABC=S梯形BB′C′C-S梯形BB′A′A-S梯形AA′C′C=2.
24.解:(1)点在反比例函数的图象上,
.
反比例函数的表达式为.
点也在反比例函数的图象上,
,即.
把点,点代入一次函数中,得
解得一次函数的表达式为.
(2)在中,当时,得.直线与轴的交点为.
线段将分成和,
.
25.(1) ∵ 点A(-4,2)和点B(n,-4)都在反比例函数y=的图象上,
∴ 解得
又由点A(-4,2)和点B(2,-4)都在一次函数y=kx+b的图象上,
∴ 解得
∴ 反比例函数的解析式为,一次函数的解析式为y=-x-2 .
(2) x的取值范围是x>2或-4<x<0 .
26.解:(1)可以看作一次函数的图象在第一象限内点的坐标,又可以看作反比例函数的图象在第一象限内点的坐标,而满足问题要求的就可以看作一次函数的图象与反比例函数的图象在第一象限内交点的坐标.
分别画出两图象(图略),从图中可看出,这样的交点存在,即满足要求的矩形存在.
(2)不同意小明的观点.
如果用分别表示矩形的长和宽,那么矩形满足,,而满足要求的可以看作一次函数的图象与反比例函数的图象在第一象限内交点的坐标.
画图(图略)可看出,这样的交点不存在,即满足要求的矩形是不存在的.
所以不同意小明的观点.
27、解:(1)(x为正整数).(x范围不写不扣分)
(2)2006年全市人均生产产值=(元)
∵,∴我市2006年人均生产产值已成功跨越6000美元大关
28、解:(1)∵点A横坐标为4 , ∴当 = 4时, = 2 .∴ 点A的坐标为( 4,2 ).
∵ 点A是直线 与双曲线 (k>0)的交点 ,∴ k = 4 ×2 = 8 .
(2) 解法一:如图12-1,∵ 点C在双曲线上,当 = 8时, = 1∴ 点C的坐标为 ( 1, 8 ) . 过点A、C分别做轴、轴的垂线,垂足为M、N,得矩形DMON .
S矩形ONDM= 32 , S△ONC = 4 , S△CDA = 9, S△OAM = 4 .
S△AOC= S矩形ONDM - S△ONC - S△CDA - S△OAM = 32 - 4 - 9 - 4 = 15 .
解法二:如图12-2,
过点 C、A分别做轴的垂线,垂足为E、F,
∵ 点C在双曲线上,当 = 8时, = 1 .
∴ 点C的坐标为 ( 1, 8 ). ∵ 点C、A都在双曲线上 ,
∴ S△COE = S△AOF = 4 ,∴ S△COE + S梯形CEFA = S△COA + S△AOF .
∴ S△COA = S梯形CEFA ,∵ S梯形CEFA = ×(2+8)×3 = 15 , ∴ S△COA = 15 .
(3)∵ 反比例函数图象是关于原点O的中心对称图形 ,
∴ OP=OQ,OA=OB .
∴ 四边形APBQ是平行四边形 .
∴ S△POA = S平行四边形APBQ = ×24 = 6 .
设点P的横坐标为( > 0且),
得P ( , ) .
过点P、A分别做轴的垂线,垂足为E、F,
∵ 点P、A在双曲线上,∴S△POE = S△AOF = 4 .
若0<<4,如图12-3,
∵ S△POE + S梯形PEFA = S△POA + S△AOF,
∴ S梯形PEFA = S△POA = 6 .
∴ .
解得= 2,= - 8(舍去) ,∴ P(2,4). 若 > 4,如图12-4,
∵ S△AOF+ S梯形AFEP = S△AOP + S△POE,∴ S梯形PEFA = S△POA = 6 . ∴,
解得 = 8, = - 2 (舍去) ,∴ P(8,1).
∴ 点P的坐标是P(2,4)或P(8,1).
图1
图2
图3
M
O
y
x
N
图4
图5
1.6
60
O
V (m3)
P (kPa)
(1.6,60)
pH
0
7
水的质量
pH
0
7
水的质量
pH
0
7
水的质量
A
B
C
D
水的质量
pH
0
7
图6
图7
图12
A
B
C
E
O
F
x
y
图11
图10
图9
图8
图13
O
y
x
B
A
图14
图8
O
x
y
2
4
6
8
2
4
6
8
图15(1)
O
x
y
1
2
3
4
1
2
3
4
图15(2)
图16
O
y
x
B
A
C
图13
