人教版八年级数学下册19.2.2.2 一次函数的图象与性质课件(18张)
文档属性
| 名称 | 人教版八年级数学下册19.2.2.2 一次函数的图象与性质课件(18张) | 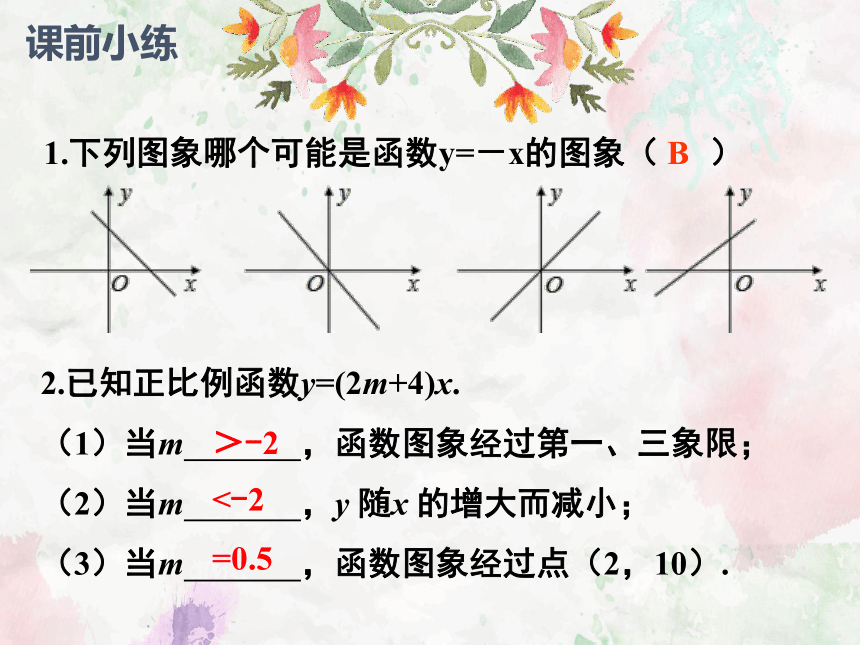 | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-19 20:49:53 | ||
图片预览




文档简介
课前小练
B
1.下列图象哪个可能是函数y=-x的图象( )
2.已知正比例函数y=(2m+4)x.
(1)当m ,函数图象经过第一、三象限;
(2)当m ,y 随x 的增大而减小;
(3)当m ,函数图象经过点(2,10).
>-2
<-2
=0.5
§19.2.2.2 一次函数的
图象与性质
第19章 一次函数
19.2 一次函数 19.2.2一次函数
学习目标
重点:了解一次函数的图象,
能根据一次函数的图象理解一次函数的增减性;
难点:能灵活运用一次函数的图象与性质解答有关问题.
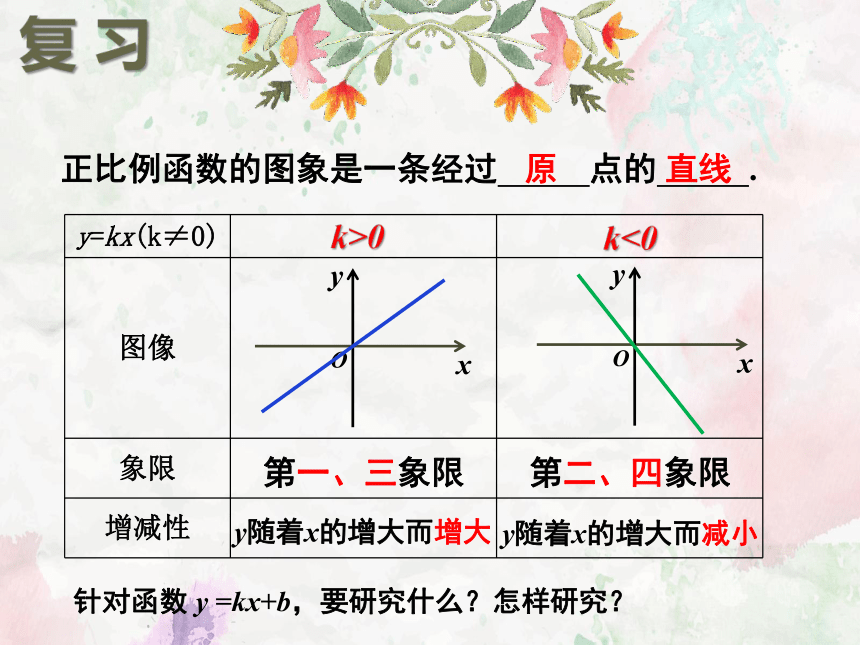
复 习
形如 的函数,叫做正比例函数;
形如 的函数,叫做一次函数;
当b=0时,y=kx+b就变成了 ,
y=kx(k是常数,k≠0)
y=kx+b (k,b是常数,k≠0)
y=kx
所以说正比例函数是一种特殊的一次函数.
复 习
正比例函数的图象是一条经过 点的 .
原
直线
{5940675A-B579-460E-94D1-54222C63F5DA}y=kx(k≠0)
图像
象限
增减性
k>0
k<0
第一、三象限
第二、四象限
y随着x的增大而增大
y随着x的增大而减小
针对函数 y =kx+b,要研究什么?怎样研究?
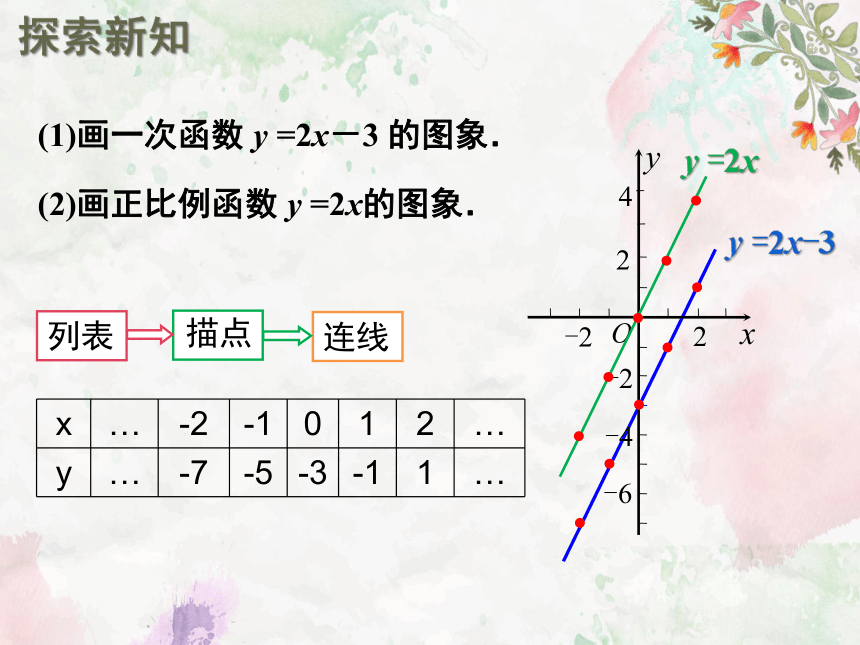
探索新知
2
-2
-4
-6
-2
2
x
y
O
{5940675A-B579-460E-94D1-54222C63F5DA}x
…
-2
-1
0
1
2
…
y
…
-7
-5
-3
-1
1
…
描点
连线
列表
(1)画一次函数 y =2x-3 的图象.
(2)画正比例函数 y =2x的图象.
y =2x-3
y =2x
4
探索新知
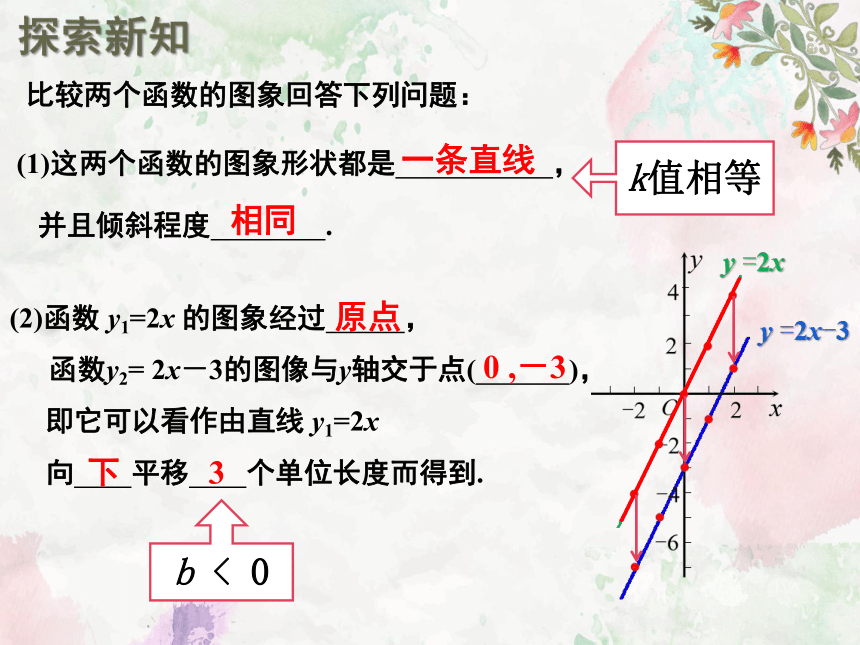
比较两个函数的图象回答下列问题:
(2)函数 y1=2x 的图象经过 ,
函数y2= 2x-3的图像与y轴交于点( ),
即它可以看作由直线 y1=2x
向 平移 个单位长度而得到.
(1)这两个函数的图象形状都是 ,
并且倾斜程度 .
原点
0 ,-3
下
3
一条直线
相同
k值相等
b < 0
探索新知
描点
连线
列表
画一次函数 y =-6x+5, y =-6x 的图象.
y =-6x+5
y =-6x
比较上面两个函数的图象回答下列问题:
(2)函数 y=-6x 的图象经过 ,
函数y= -6x+5的图像与y轴交于点( ),
即它可以看作由直线 y=-6x
向 平移 个单位长度而得到.
(1)这两个函数的图象形状都是 ,
并且倾斜程度 .
原点
0 ,5
上
5
一条直线
相同
k值相等
b >0
探索新知
一次函数y=kx+b(k≠0)的图象经过点(0,b)的直线
下
上
要点归纳
可以由正比例函数y=kx的图象平移 个单位长度得到
当b>0时,向 平移,
当b<0时,向 平移,
与y轴的交点在正半轴
与y轴的交点在负半轴
与y轴的交点:
则y=b
令x=0,
(0, b)
思考:与x轴的交点坐标是什么?
与x轴的交点:
则
令y=0,
例题
已知正比例函数y=kx经过点P(2,3),如图
(1)求这个正比例函数的解析式;
(2)将该直线向上平移3个单位长度,
求平移后所得直线的解析式.
解:(1)由函数y=kx经过点P(2,3),
可得k= ,
∴该正比例函数的解析式为y= x.
(2)直线y= x向上平移3个单位长度后,
得到的直线的解析式为y= x+3.
v
探索新知
{5940675A-B579-460E-94D1-54222C63F5DA}y=kx+b
(k≠0)
k>0
k<0
b>0
b<0
b=0
第一,二,三象限
第一,三象限
第一,三,四象限
第一,二,四象限
第二,四象限
第二,三,四象限
增减性
y随着x的增大而增大
y随着x的增大而减小
练习
k 0,b 0
>
>
k 0,b 0
k 0,b 0
k 0,b 0
k 0,b 0
k 0,b 0
>
>
>
<
<
<
<
<
=
=
根据一次函数的图象判断k,b的正负,
并说出直线经过的象限:
例题
已知一次函数 y=(1-2m)x+m-1,求满足下列条件的m值:
(1)函数值y 随x的增大而增大;
(2)函数图象与y 轴的负半轴相交;
(3)函数的图象过第二、三、四象限;
解:(1)依题意得1-2m>0,解得
∴
解得 ,
m<1,
(2)依题意得
1-2m≠0,
m-1<0,
∴
解得 ,
m<1,
(3)依题意得
1-2m<0,
m-1<0,
练习
已知一次函数y=(2m+4)x+(2n-4).
(1)m为何值时,y随x的增大而减小?
(2)m,n为何值时,函数图象与y轴的交点在y轴的负半轴上?
解:(1)由题意得2m+4<0,解得m<-2.
(2)由题意得 解得:
∴m≠-2且n<2
当堂练习
1. 一次函数y=x-2的大致图象为( )
C
A B C D
2.下列函数中,y的值随x值的增大而增大的函数是( )
A. y=-2x B. y=-2x+1 C. y=x-2 D. y=-x-2
C
练习
3.直线y =2x-3 与x 轴交点的坐标为__________;
与y 轴交点的坐标为___________;
图象经过第_____________象限, y 随x 的增大而________.
4.若直线y=kx+2与y=3x-1平行,则k= .
3
5.点A(-1,y1),B(3,y2)是直线y=kx+b(k<0)上的两点,
则y1-y2 0(填“>”或“<”).
>
(0,-3)
一、三、四
增大
(1.5,0)
练习
6.已知一次函数y=(3m-8)x+1-m图象
与 y轴交点在x轴下方,且y随x的增大而减小,
其中m为整数,求m的值 .
解: 依题意得 ,
又∵m为整数,
∴m=2.
解得
∴
课堂小结
一次函数函数的图象和性质
当k>0时,y的值随x值的增大而增大;
当k<0时,y的值随x值的增大而减小.
与y轴的交点是(0,b),
与x轴的交点是( ,0),
当k>0, b>0时,经过一、二、三象限;
当k>0 ,b<0时,经过一、三、四象限;
当k<0 ,b>0时,经过 一、二、四象限;
当k<0 ,b<0时,经过二、三、四象限.
图象
性质
B
1.下列图象哪个可能是函数y=-x的图象( )
2.已知正比例函数y=(2m+4)x.
(1)当m ,函数图象经过第一、三象限;
(2)当m ,y 随x 的增大而减小;
(3)当m ,函数图象经过点(2,10).
>-2
<-2
=0.5
§19.2.2.2 一次函数的
图象与性质
第19章 一次函数
19.2 一次函数 19.2.2一次函数
学习目标
重点:了解一次函数的图象,
能根据一次函数的图象理解一次函数的增减性;
难点:能灵活运用一次函数的图象与性质解答有关问题.
复 习
形如 的函数,叫做正比例函数;
形如 的函数,叫做一次函数;
当b=0时,y=kx+b就变成了 ,
y=kx(k是常数,k≠0)
y=kx+b (k,b是常数,k≠0)
y=kx
所以说正比例函数是一种特殊的一次函数.
复 习
正比例函数的图象是一条经过 点的 .
原
直线
{5940675A-B579-460E-94D1-54222C63F5DA}y=kx(k≠0)
图像
象限
增减性
k>0
k<0
第一、三象限
第二、四象限
y随着x的增大而增大
y随着x的增大而减小
针对函数 y =kx+b,要研究什么?怎样研究?
探索新知
2
-2
-4
-6
-2
2
x
y
O
{5940675A-B579-460E-94D1-54222C63F5DA}x
…
-2
-1
0
1
2
…
y
…
-7
-5
-3
-1
1
…
描点
连线
列表
(1)画一次函数 y =2x-3 的图象.
(2)画正比例函数 y =2x的图象.
y =2x-3
y =2x
4
探索新知
比较两个函数的图象回答下列问题:
(2)函数 y1=2x 的图象经过 ,
函数y2= 2x-3的图像与y轴交于点( ),
即它可以看作由直线 y1=2x
向 平移 个单位长度而得到.
(1)这两个函数的图象形状都是 ,
并且倾斜程度 .
原点
0 ,-3
下
3
一条直线
相同
k值相等
b < 0
探索新知
描点
连线
列表
画一次函数 y =-6x+5, y =-6x 的图象.
y =-6x+5
y =-6x
比较上面两个函数的图象回答下列问题:
(2)函数 y=-6x 的图象经过 ,
函数y= -6x+5的图像与y轴交于点( ),
即它可以看作由直线 y=-6x
向 平移 个单位长度而得到.
(1)这两个函数的图象形状都是 ,
并且倾斜程度 .
原点
0 ,5
上
5
一条直线
相同
k值相等
b >0
探索新知
一次函数y=kx+b(k≠0)的图象经过点(0,b)的直线
下
上
要点归纳
可以由正比例函数y=kx的图象平移 个单位长度得到
当b>0时,向 平移,
当b<0时,向 平移,
与y轴的交点在正半轴
与y轴的交点在负半轴
与y轴的交点:
则y=b
令x=0,
(0, b)
思考:与x轴的交点坐标是什么?
与x轴的交点:
则
令y=0,
例题
已知正比例函数y=kx经过点P(2,3),如图
(1)求这个正比例函数的解析式;
(2)将该直线向上平移3个单位长度,
求平移后所得直线的解析式.
解:(1)由函数y=kx经过点P(2,3),
可得k= ,
∴该正比例函数的解析式为y= x.
(2)直线y= x向上平移3个单位长度后,
得到的直线的解析式为y= x+3.
v
探索新知
{5940675A-B579-460E-94D1-54222C63F5DA}y=kx+b
(k≠0)
k>0
k<0
b>0
b<0
b=0
第一,二,三象限
第一,三象限
第一,三,四象限
第一,二,四象限
第二,四象限
第二,三,四象限
增减性
y随着x的增大而增大
y随着x的增大而减小
练习
k 0,b 0
>
>
k 0,b 0
k 0,b 0
k 0,b 0
k 0,b 0
k 0,b 0
>
>
>
<
<
<
<
<
=
=
根据一次函数的图象判断k,b的正负,
并说出直线经过的象限:
例题
已知一次函数 y=(1-2m)x+m-1,求满足下列条件的m值:
(1)函数值y 随x的增大而增大;
(2)函数图象与y 轴的负半轴相交;
(3)函数的图象过第二、三、四象限;
解:(1)依题意得1-2m>0,解得
∴
解得 ,
m<1,
(2)依题意得
1-2m≠0,
m-1<0,
∴
解得 ,
m<1,
(3)依题意得
1-2m<0,
m-1<0,
练习
已知一次函数y=(2m+4)x+(2n-4).
(1)m为何值时,y随x的增大而减小?
(2)m,n为何值时,函数图象与y轴的交点在y轴的负半轴上?
解:(1)由题意得2m+4<0,解得m<-2.
(2)由题意得 解得:
∴m≠-2且n<2
当堂练习
1. 一次函数y=x-2的大致图象为( )
C
A B C D
2.下列函数中,y的值随x值的增大而增大的函数是( )
A. y=-2x B. y=-2x+1 C. y=x-2 D. y=-x-2
C
练习
3.直线y =2x-3 与x 轴交点的坐标为__________;
与y 轴交点的坐标为___________;
图象经过第_____________象限, y 随x 的增大而________.
4.若直线y=kx+2与y=3x-1平行,则k= .
3
5.点A(-1,y1),B(3,y2)是直线y=kx+b(k<0)上的两点,
则y1-y2 0(填“>”或“<”).
>
(0,-3)
一、三、四
增大
(1.5,0)
练习
6.已知一次函数y=(3m-8)x+1-m图象
与 y轴交点在x轴下方,且y随x的增大而减小,
其中m为整数,求m的值 .
解: 依题意得 ,
又∵m为整数,
∴m=2.
解得
∴
课堂小结
一次函数函数的图象和性质
当k>0时,y的值随x值的增大而增大;
当k<0时,y的值随x值的增大而减小.
与y轴的交点是(0,b),
与x轴的交点是( ,0),
当k>0, b>0时,经过一、二、三象限;
当k>0 ,b<0时,经过一、三、四象限;
当k<0 ,b>0时,经过 一、二、四象限;
当k<0 ,b<0时,经过二、三、四象限.
图象
性质
