人教版八年级数学下册第18章《平行四边形》18.1.2 平行四边形的判定(一)课件(26张)
文档属性
| 名称 | 人教版八年级数学下册第18章《平行四边形》18.1.2 平行四边形的判定(一)课件(26张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 588.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-19 20:52:59 | ||
图片预览







文档简介
第十八章 平行四边形
第三课时
18.1.2 平行四边形的判定(一)
学习目标
1.知道平行四边形的四种判定方法及推理格式.
2.能用这些判定方法证明一个四边形是平行四边形.
新课导入
平行四边形有哪些性质?
对边相等
对角相等
对角线互相平分
知识点
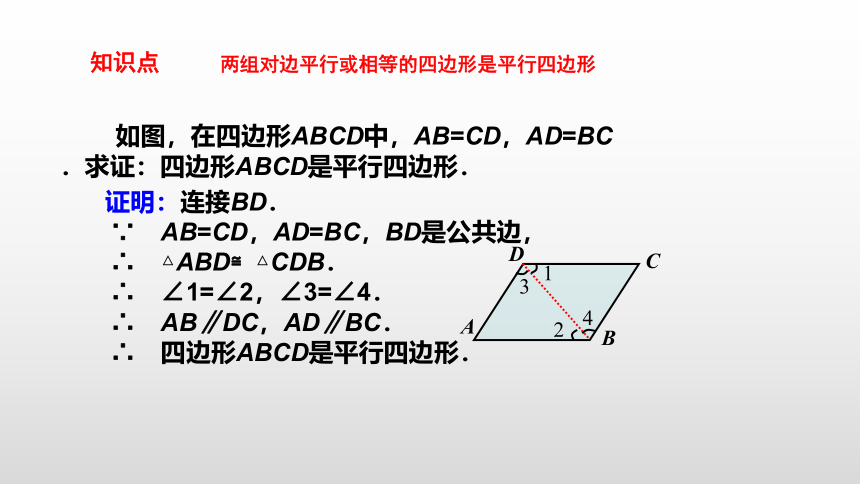
两组对边平行或相等的四边形是平行四边形
证明:连接BD.
∵ AB=CD,AD=BC,BD是公共边,
∴ △ABD≌△CDB.
∴ ∠1=∠2,∠3=∠4.
∴ AB∥DC,AD∥BC.
∴ 四边形ABCD是平行四边形.
如图,在四边形ABCD中,AB=CD,AD=BC.求证:四边形ABCD是平行四边形.
D
A
B
C
1
2
3
4
从边看:
方法一:两组对边分别平行的四边形是
平行四边形;(定义法)
数学表达式:如图,∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形;
方法二:两组对边分别相等的四边形是平行四边形;
数学表达式:如图,∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形;
如图,分别以△ABC的三边为一边,在BC的同侧
作等边三角形ABD,等边三角形BCE,等边三角
形ACF,连接DE,EF.
求证:四边形ADEF是平行四边形.
平行四边形的判定定理:
两组对边分别相等的四边形是平行四边形.
几何语言描述:
在四边形ABCD中,∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形.
B
D
A
C
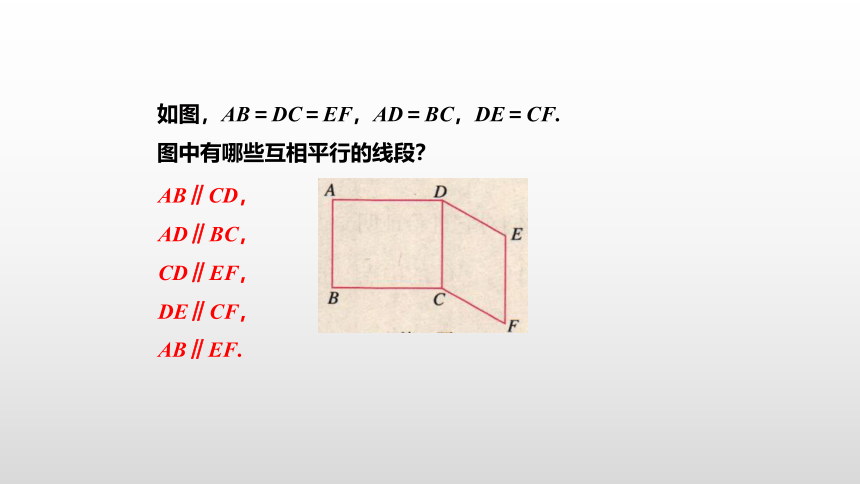
如图,AB=DC=EF,AD=BC,DE=CF. 图中有哪些互相平行的线段?
AB∥CD,AD∥BC,
CD∥EF,DE∥CF,
AB∥EF.
知识点
两组对角分别相等的四边形是平行四边形
几何语言:
∵∠ABC=∠ADC,∠BAD=∠BCD,
∴四边形ABCD是平行四边形.(如图所示)
证明:∵ 多边形ABCD是四边形,
∴∠A+∠B+∠C+∠D=360°.
又∵∠A=∠C,∠B=∠D,
∴∠A+∠B=180°,
∠B+∠C=180°.
∴AD∥BC,AB∥DC.
∴四边形ABCD是平行四边形.
如图,在四边形ABCD中,∠A=∠C,∠B=∠D.求证:四边形ABCD是平行四边形.
D
A
B
C
平行四边形的判定定理:
两组对角分别相等的四边形是平行四边形.
几何语言描述:
在四边形ABCD中,∵∠A=∠C,∠B=∠D,
∴四边形ABCD是平行四边形.
B
D
A
C
例 如图,四边形ABCD中,AB∥DC,∠B=55°,∠1=85°,∠2=40°.
(1)求∠D的度数;
(2)求证:四边形ABCD是平行四边形.
(1)解:∵∠D+∠2+∠1=180°,
∴∠D=180°-∠2-∠1=55°;
(2)证明:∵AB∥DC,
∴∠2=∠CAB,
∴∠DAB=∠1+∠2=125°.
∵∠DCB+∠DAB+∠D+∠B=360°,
∴∠DCB=∠DAB=125°.
又∵∠D=∠B=55°,
∴四边形ABCD是平行四边形.
当已知条件出现所要说明的四边形的角时,可选择“两组对角分别相等的四边形是平行四边形”来判定.
下列给出的条件中,能判定四边形ABCD是平行
四边形的是( )
A.AB∥CD,AD=BC
B.AB=AD,CB=CD
C.AB=CD,AD=BC
D.∠B=∠C,∠A=∠D
C
知识点
对角线互相平分的四边形是平行四边形
下面我们以“对角线互相平分的四边形是平行四边
形”为例,通过三角形 全等进行证明.
如图,在四边形ABCD中,AC,BD相交于点O,
且OA=OC,OB=OD.
求证:四边形ABCD是平行四边形.
证明:
∵OA=OC,OD=OB,
∠AOD=∠COB,
∴△ AOD≌△COB.
∴∠OAD=∠OCB.
∴AD//BC.
同理 AB//DC.
∴四边形ABCD是平行四边形.
对角线互相平分的四边形是平行四边形.
数学表达式:
∵OA=OC,OB=OD,
∴四边形ABCD是平行四边形.
平行四边形的方法:
定义:两组对边分别平行的四边形叫做平行四边形.
判定定理:
(1)两组对边分别相等的四边形是平行四边形;
(2)两组对角分别相等的四边形是平行四边形;
(3)对角线互相平分的四边形是平行四边形.
例 如图, □ABCD 的对角线AC,BD相交于点O,E,F是AC上的两点,并且AE=CF.求证:四边形BFDE是平行四边形.
B
O
D
A
C
E
F
证明:∵四边形ABCD是平行四边形,
∴ AO=CO,BO=DO.
∵AE=CF ,
∴ AO-AE=CO-CF,即EO=OF.
又∵BO=DO,
∴四边形BFDE是平行四边形.
如图,?ABCD的对角线AC,BD相交于点O,E,F分别是OA,OC的中 点. 求证BE=DF.
因为四边形ABCD是平行四边形,
所以BO=DO,OA=OC.
因为E,F分别是OA,OC的中点,
所以OE= OA= OC=OF.
又因为∠BOE=∠DOF,
所以△BOE≌△DOF,所以BE=DF.
解:
随堂演练
1.如图,线段AB,CD相交于点O,且图上各点把线段AB,CD四等分,这些点可以构成________个平行四边形.
2.如图,在四边形ABCD中,AC与BD交于点O.
如果AC=8cm,BD=10cm,那么当AO=_____cm,
BO=_____cm时,四边形ABCD是平行四边形.
B
O
D
A
C
3.如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
A.OA=OC,OB=OD
B.AB=CD,AO=CO
C.AB=CD,AD=BC
D.∠BAD=∠BCD,AB∥CD
B
O
D
A
C
4下列条件不能判定四边形ABCD是平行四边形的是( )
A.AB∥CD,AD∥BC
B.∠A=∠C,∠B=∠D
C.AB=CD,AD=BC
D.AB∥CD,AD=BC
D
5.如图,DB∥AC,DB= AC,E是AC的中点,求证:BC=DE.
两组对边分别平行的四边形是平行四边形;
两组对边分别相等的四边形是平行四边形;
对角线互相平分的四边形是平行四边形.
两组对角分别相等的四边形是平行四边形
平行四边形的判定方法
第三课时
18.1.2 平行四边形的判定(一)
学习目标
1.知道平行四边形的四种判定方法及推理格式.
2.能用这些判定方法证明一个四边形是平行四边形.
新课导入
平行四边形有哪些性质?
对边相等
对角相等
对角线互相平分
知识点
两组对边平行或相等的四边形是平行四边形
证明:连接BD.
∵ AB=CD,AD=BC,BD是公共边,
∴ △ABD≌△CDB.
∴ ∠1=∠2,∠3=∠4.
∴ AB∥DC,AD∥BC.
∴ 四边形ABCD是平行四边形.
如图,在四边形ABCD中,AB=CD,AD=BC.求证:四边形ABCD是平行四边形.
D
A
B
C
1
2
3
4
从边看:
方法一:两组对边分别平行的四边形是
平行四边形;(定义法)
数学表达式:如图,∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形;
方法二:两组对边分别相等的四边形是平行四边形;
数学表达式:如图,∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形;
如图,分别以△ABC的三边为一边,在BC的同侧
作等边三角形ABD,等边三角形BCE,等边三角
形ACF,连接DE,EF.
求证:四边形ADEF是平行四边形.
平行四边形的判定定理:
两组对边分别相等的四边形是平行四边形.
几何语言描述:
在四边形ABCD中,∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形.
B
D
A
C
如图,AB=DC=EF,AD=BC,DE=CF. 图中有哪些互相平行的线段?
AB∥CD,AD∥BC,
CD∥EF,DE∥CF,
AB∥EF.
知识点
两组对角分别相等的四边形是平行四边形
几何语言:
∵∠ABC=∠ADC,∠BAD=∠BCD,
∴四边形ABCD是平行四边形.(如图所示)
证明:∵ 多边形ABCD是四边形,
∴∠A+∠B+∠C+∠D=360°.
又∵∠A=∠C,∠B=∠D,
∴∠A+∠B=180°,
∠B+∠C=180°.
∴AD∥BC,AB∥DC.
∴四边形ABCD是平行四边形.
如图,在四边形ABCD中,∠A=∠C,∠B=∠D.求证:四边形ABCD是平行四边形.
D
A
B
C
平行四边形的判定定理:
两组对角分别相等的四边形是平行四边形.
几何语言描述:
在四边形ABCD中,∵∠A=∠C,∠B=∠D,
∴四边形ABCD是平行四边形.
B
D
A
C
例 如图,四边形ABCD中,AB∥DC,∠B=55°,∠1=85°,∠2=40°.
(1)求∠D的度数;
(2)求证:四边形ABCD是平行四边形.
(1)解:∵∠D+∠2+∠1=180°,
∴∠D=180°-∠2-∠1=55°;
(2)证明:∵AB∥DC,
∴∠2=∠CAB,
∴∠DAB=∠1+∠2=125°.
∵∠DCB+∠DAB+∠D+∠B=360°,
∴∠DCB=∠DAB=125°.
又∵∠D=∠B=55°,
∴四边形ABCD是平行四边形.
当已知条件出现所要说明的四边形的角时,可选择“两组对角分别相等的四边形是平行四边形”来判定.
下列给出的条件中,能判定四边形ABCD是平行
四边形的是( )
A.AB∥CD,AD=BC
B.AB=AD,CB=CD
C.AB=CD,AD=BC
D.∠B=∠C,∠A=∠D
C
知识点
对角线互相平分的四边形是平行四边形
下面我们以“对角线互相平分的四边形是平行四边
形”为例,通过三角形 全等进行证明.
如图,在四边形ABCD中,AC,BD相交于点O,
且OA=OC,OB=OD.
求证:四边形ABCD是平行四边形.
证明:
∵OA=OC,OD=OB,
∠AOD=∠COB,
∴△ AOD≌△COB.
∴∠OAD=∠OCB.
∴AD//BC.
同理 AB//DC.
∴四边形ABCD是平行四边形.
对角线互相平分的四边形是平行四边形.
数学表达式:
∵OA=OC,OB=OD,
∴四边形ABCD是平行四边形.
平行四边形的方法:
定义:两组对边分别平行的四边形叫做平行四边形.
判定定理:
(1)两组对边分别相等的四边形是平行四边形;
(2)两组对角分别相等的四边形是平行四边形;
(3)对角线互相平分的四边形是平行四边形.
例 如图, □ABCD 的对角线AC,BD相交于点O,E,F是AC上的两点,并且AE=CF.求证:四边形BFDE是平行四边形.
B
O
D
A
C
E
F
证明:∵四边形ABCD是平行四边形,
∴ AO=CO,BO=DO.
∵AE=CF ,
∴ AO-AE=CO-CF,即EO=OF.
又∵BO=DO,
∴四边形BFDE是平行四边形.
如图,?ABCD的对角线AC,BD相交于点O,E,F分别是OA,OC的中 点. 求证BE=DF.
因为四边形ABCD是平行四边形,
所以BO=DO,OA=OC.
因为E,F分别是OA,OC的中点,
所以OE= OA= OC=OF.
又因为∠BOE=∠DOF,
所以△BOE≌△DOF,所以BE=DF.
解:
随堂演练
1.如图,线段AB,CD相交于点O,且图上各点把线段AB,CD四等分,这些点可以构成________个平行四边形.
2.如图,在四边形ABCD中,AC与BD交于点O.
如果AC=8cm,BD=10cm,那么当AO=_____cm,
BO=_____cm时,四边形ABCD是平行四边形.
B
O
D
A
C
3.如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
A.OA=OC,OB=OD
B.AB=CD,AO=CO
C.AB=CD,AD=BC
D.∠BAD=∠BCD,AB∥CD
B
O
D
A
C
4下列条件不能判定四边形ABCD是平行四边形的是( )
A.AB∥CD,AD∥BC
B.∠A=∠C,∠B=∠D
C.AB=CD,AD=BC
D.AB∥CD,AD=BC
D
5.如图,DB∥AC,DB= AC,E是AC的中点,求证:BC=DE.
两组对边分别平行的四边形是平行四边形;
两组对边分别相等的四边形是平行四边形;
对角线互相平分的四边形是平行四边形.
两组对角分别相等的四边形是平行四边形
平行四边形的判定方法
