人教版八年级数学下册课件第17章第一节《勾股定理》第1课时勾股定理(19张PPT)
文档属性
| 名称 | 人教版八年级数学下册课件第17章第一节《勾股定理》第1课时勾股定理(19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 300.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-19 00:00:00 | ||
图片预览






文档简介
第1节 勾股定理
第1课时 勾股定理
第十七章 勾股定理
1.了解勾股定理的文化背景,了解常见的利用拼图验证勾股定理的方法.
2.知道勾股定理的内容.
3.会用勾股定理进行简单的计算 .(难点)
学习目标
你知道在古代,人们如何称呼直角三角形的三边吗?
勾
股
弦
勾股定理有着悠久的历史:古巴比伦人和古代中国人看出了这个关系,古希腊的毕达哥拉斯学派首先证明了这关系.
勾股定理的发现
毕达哥拉斯在朋友家里做客时,从砖铺成的地面中发现了直角三角形三边的数量关系.
三个正方形的面积有什么关系?
两个小正方形的面积之和等于大正方形的面积.
等腰直角三角形三条边长度之间有怎样的特殊关系?
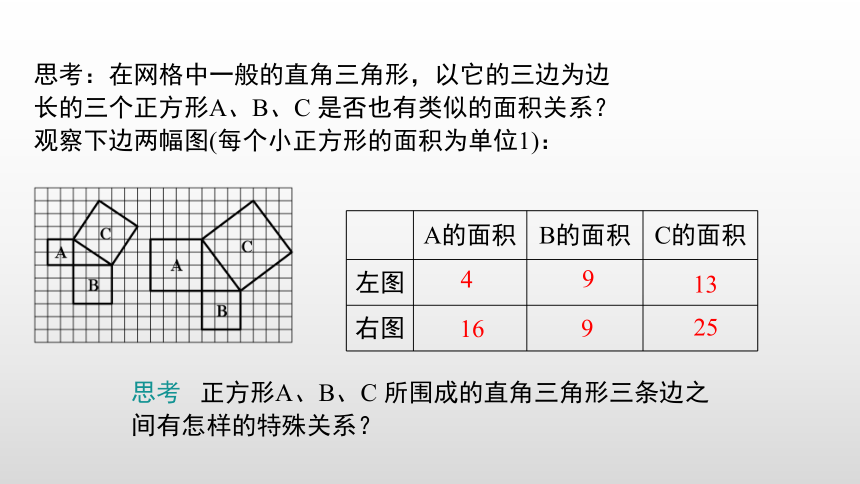
思考:在网格中一般的直角三角形,以它的三边为边长的三个正方形A、B、C 是否也有类似的面积关系?观察下边两幅图(每个小正方形的面积为单位1):
A的面积
B的面积
C的面积
左图
右图
4
13
25
9
16
9
思考 正方形A、B、C 所围成的直角三角形三条边之间有怎样的特殊关系?
如果直角三角形两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
通过前面的探究活动,你发现了直角三角形三边之间的关系规律了吗?
a、b、c为正数
如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
变形:
勾股定理
a
b
c
A
例 如图,在Rt△ABC中, ∠C=90°.
(1)若a=b=5,求c;
(2)若a=1,c=2,求b.
解:
(1)据勾股定理得
(2)据勾股定理得
利用勾股定理进行计算
C
A
B
【变式】 在Rt△ABC中,AB=4,AC=3,求BC的长.
解:本题斜边不确定,需分类讨论:
当AB为斜边时,
当BC为斜边时,
随堂练
1.在Rt△ABC中,两直角边长分别为3和 ,则斜边长为 .
2.在Rt△ABC中,∠C=90°,a=6,c=10,则b= .
3. 已知∠ACB=90°,CD⊥AB,AC=3,BC=4.求CD的长.
A
D
B
C
3
4
4.下列说法中,正确的是 ( )
A.已知a,b,c是三角形的三边,则a2+b2=c2
B.在直角三角形中两边和的平方等于第三边的平方
C.在Rt△ABC中,∠C=90°,所以a2+b2=c2
D.在Rt△ABC中,∠B=90°,所以a2+b2=c2
C
5.在△ABC中,∠C=90°.
(1)若a=6,b=8,则c= .
(2)若c=13,b=12,则a= .
6.若直角三角形中,有两边长是5和7,则第三边长
的平方为_________.
10
5
74或24
7.在Rt△ABC中,∠C=90°.
(1)已知c=25,b=15,求a;
(2)已知a= ,∠A=60°,求b,c.
课堂小结
1.本节课你有什么收获?你学到了什么?
说给大家听听。
2.你还有什么疑问,问问老师。
1.从课后习题中选取;
2.完成练习册本课时的习题。
作业
第1课时 勾股定理
第十七章 勾股定理
1.了解勾股定理的文化背景,了解常见的利用拼图验证勾股定理的方法.
2.知道勾股定理的内容.
3.会用勾股定理进行简单的计算 .(难点)
学习目标
你知道在古代,人们如何称呼直角三角形的三边吗?
勾
股
弦
勾股定理有着悠久的历史:古巴比伦人和古代中国人看出了这个关系,古希腊的毕达哥拉斯学派首先证明了这关系.
勾股定理的发现
毕达哥拉斯在朋友家里做客时,从砖铺成的地面中发现了直角三角形三边的数量关系.
三个正方形的面积有什么关系?
两个小正方形的面积之和等于大正方形的面积.
等腰直角三角形三条边长度之间有怎样的特殊关系?
思考:在网格中一般的直角三角形,以它的三边为边长的三个正方形A、B、C 是否也有类似的面积关系?观察下边两幅图(每个小正方形的面积为单位1):
A的面积
B的面积
C的面积
左图
右图
4
13
25
9
16
9
思考 正方形A、B、C 所围成的直角三角形三条边之间有怎样的特殊关系?
如果直角三角形两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
通过前面的探究活动,你发现了直角三角形三边之间的关系规律了吗?
a、b、c为正数
如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
变形:
勾股定理
a
b
c
A
例 如图,在Rt△ABC中, ∠C=90°.
(1)若a=b=5,求c;
(2)若a=1,c=2,求b.
解:
(1)据勾股定理得
(2)据勾股定理得
利用勾股定理进行计算
C
A
B
【变式】 在Rt△ABC中,AB=4,AC=3,求BC的长.
解:本题斜边不确定,需分类讨论:
当AB为斜边时,
当BC为斜边时,
随堂练
1.在Rt△ABC中,两直角边长分别为3和 ,则斜边长为 .
2.在Rt△ABC中,∠C=90°,a=6,c=10,则b= .
3. 已知∠ACB=90°,CD⊥AB,AC=3,BC=4.求CD的长.
A
D
B
C
3
4
4.下列说法中,正确的是 ( )
A.已知a,b,c是三角形的三边,则a2+b2=c2
B.在直角三角形中两边和的平方等于第三边的平方
C.在Rt△ABC中,∠C=90°,所以a2+b2=c2
D.在Rt△ABC中,∠B=90°,所以a2+b2=c2
C
5.在△ABC中,∠C=90°.
(1)若a=6,b=8,则c= .
(2)若c=13,b=12,则a= .
6.若直角三角形中,有两边长是5和7,则第三边长
的平方为_________.
10
5
74或24
7.在Rt△ABC中,∠C=90°.
(1)已知c=25,b=15,求a;
(2)已知a= ,∠A=60°,求b,c.
课堂小结
1.本节课你有什么收获?你学到了什么?
说给大家听听。
2.你还有什么疑问,问问老师。
1.从课后习题中选取;
2.完成练习册本课时的习题。
作业
