人教版八年级下册第十七章勾股定理复习课 课件(21张PPT)
文档属性
| 名称 | 人教版八年级下册第十七章勾股定理复习课 课件(21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 722.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-19 00:00:00 | ||
图片预览






文档简介
勾股定理复习
a
b
c
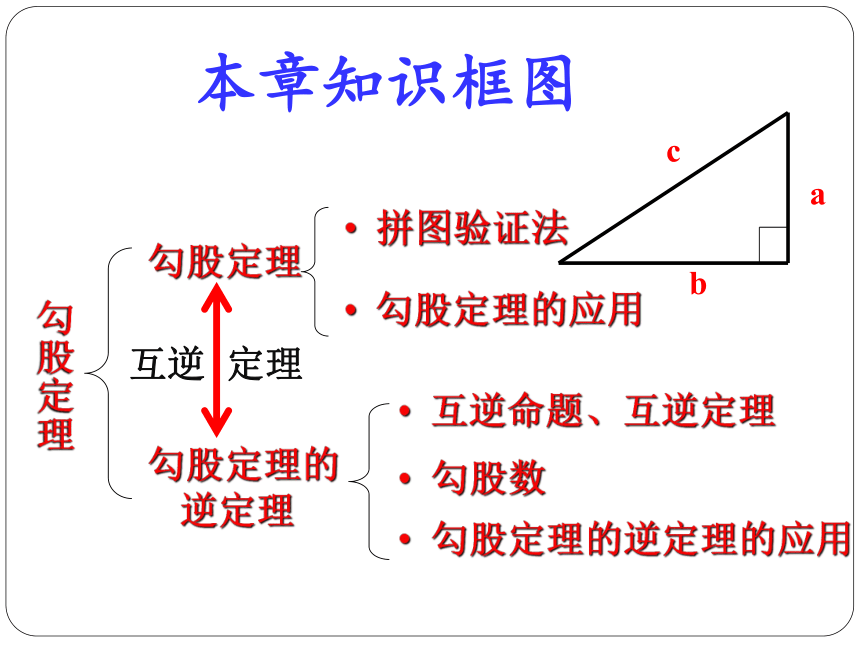
勾股定理
勾股定理
勾股定理的逆定理
拼图验证法
勾股定理的应用
互逆命题、互逆定理
勾股数
勾股定理的逆定理的应用
本章知识框图
互逆 定理
1.勾股定理
直角三角形两直角边a、 b的平方和,等于斜边c的平方.
2.勾股定理的逆定理
如果三角形三边长a、b、c满足a2+b2=c2,那么这个三角形是直角三角形。
满足a2+b2=c2的三个正整数,称为勾股数.
熟记常见的勾股数(如3、4、5)
3.勾股数
4.互逆命题与互逆定理的概念
2、常用的勾股数:
3、4、5; 6、8、10;
5、12、13; 7、24、25;
8、15、17; 9、40、41.
ak,bk,ck; 2n,n2-1,n2+1.
2n+1, 2n2+2n, 2n2+2n+1(n,k>0)
满足a2 +b2=c2的三个正整数,称为勾股数
疑点点拨
2、在△ABC中,AC=6,BC=8,则AB的长为( )
A 10 B 2 C 4 D 无法确定
3、已知直角三角形的两边长分别为3、4,则第三边长为 。
1、命题“直角三角形中30°角所对的直角边等于斜边的一半”的逆命题是 。
D
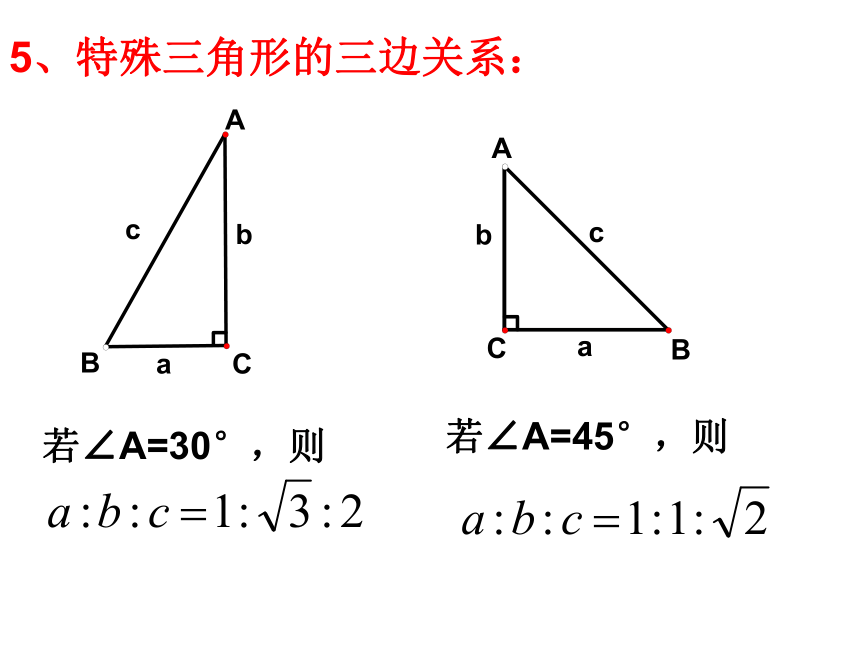
5、特殊三角形的三边关系:
若∠A=30°,则
若∠A=45°,则
考 点 一
与勾股定理有关的
计算问题
比一比,看谁快!
1、在Rt△ABC中,∠C=900
①若a=6,b=8, 则c=___;
10
9
4
③若a:b=1:2,c= 2 ,则S△ABC=____;
②若a=40,c=41,则b=____;
a
b
c
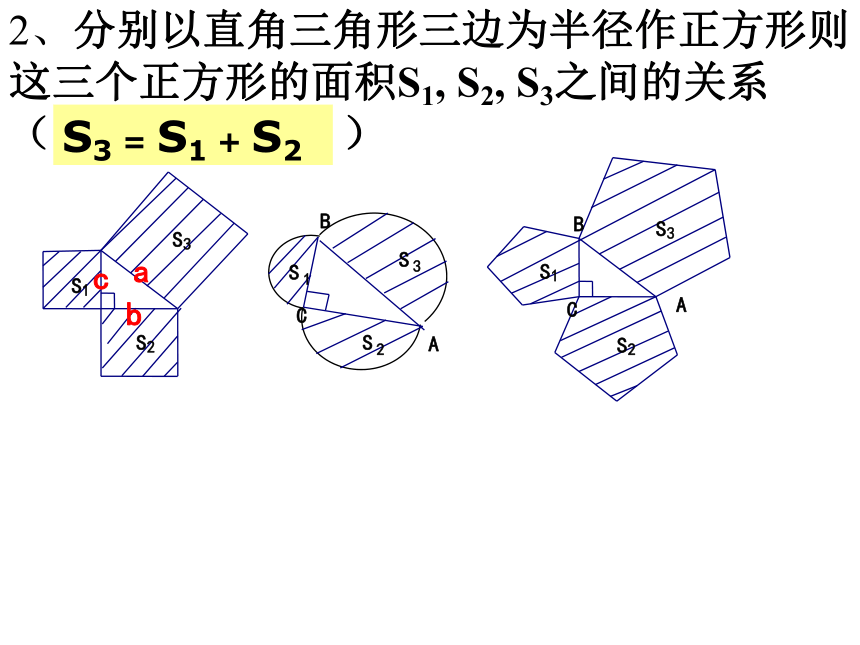
2、分别以直角三角形三边为半径作正方形则这三个正方形的面积S1, S2, S3之间的关系( )
S3 = S1 + S2
C
B
A
S
3
S
2
S
1
C
B
A
S
3
S
2
S
1
a
b
S
3
S
2
S
1
c
3、等腰三角形底边上的高为8,周长为32,求这个三角形的面积
8
x
16-x
D
A
B
C
解:设这个三角形为ABC,高为AD,设BD为x,则AB为(16-x),
由勾股定理得:
x2+82=(16-x)2
即x2+64=256-32x+x2
∴ x=6
∴ S?ABC=BC?AD/2=2 ?6 ?8/2=48
4、(教材P29)如图,已知直角三角形ABC的三边分别为6、8、10,分别以它的三边为直径向上作三个半圆,求图中阴影部分的面积.
5、已知:如图,∠B=∠D=90°,∠A=60°,AB=4,CD=2,求:四边形ABCD的面积。
考 点 3
与勾股定理有关的证明题
1、如图,已知在△ABC中,∠C=90°,D为AC上一点,AB2-BD2与AC2-DC2有怎样的关系?试证明你的结论。
证明:
在Rt △ABC中,
AB2=AC2+BC2
在Rt △DBC中,
BD2=DC2+BC2
∴ BC2 = AB2—AC2
BC2 = BD2 — DC2
∴ AB2—AC2 = BD2 — DC2
∵ ∠C=90°
即: AB2-BD2 = AC2-DC2
2、已知,△ABC中,AB=17cm,BC=16cm,BC边上的中线AD=15cm,试说明△ABC是等腰三角形。
提示: 先运用勾股定理证明中线AD⊥BC,再利用等腰三角形的判定方法就可以说明了.
考 点 4
勾股定理的实际应用
2、如图,点A是一个半径为 250 m的圆形森林公园的中心,在森林公园附近有 B 、C 两个小镇,现要在 B、C 两小镇之间修一条长为 1000 m 的笔直公路将两镇连通,经测得 ∠B=60°,∠C=30°,问:请通过计算说明此公路会不会穿过该森林公园?
A
B
C
250
1000
60°
30°
D
解:在△ABC中∠B=60°,∠C=30°,
∴∠BAC=900
∴在Rt△ABC中,AB= BC=500
AC= =500
∵2S△ABC=AD×BC=AB×AC
∴AD=250 >250
∴此公路不会穿过该森林公园
3、如图,A市气象测得台风中心在A市正东方向300千米的B处,以 千米每时的速度向北偏西60°的方向移动,距台风中心200千米范围内是会受到台风影响范围。
(1)A市是否会受台风影响?说明理由;
(2)若A市受影响,那么受台风影响的时间为多久?
B
北
60°
东
A
C
勾股定理逆定理的应用
考点5
如果三角形的三边长a,b,c满足a2 +b2=c2 ,
那么这个三角形是直角三角形
我满足
a2 +b2=c2 ,
a
b
c
我是直角三角形
跟踪训练:教材P39第9题
1、在矩形纸片ABCD中,AD=4cm,AB=10cm,按图所示方式折叠,使点B与点D重合,折痕为EF,求DE的长?
A
B
C
D
E
F
C’
六、利用方程解决翻折问题
a
b
c
勾股定理
勾股定理
勾股定理的逆定理
拼图验证法
勾股定理的应用
互逆命题、互逆定理
勾股数
勾股定理的逆定理的应用
本章知识框图
互逆 定理
1.勾股定理
直角三角形两直角边a、 b的平方和,等于斜边c的平方.
2.勾股定理的逆定理
如果三角形三边长a、b、c满足a2+b2=c2,那么这个三角形是直角三角形。
满足a2+b2=c2的三个正整数,称为勾股数.
熟记常见的勾股数(如3、4、5)
3.勾股数
4.互逆命题与互逆定理的概念
2、常用的勾股数:
3、4、5; 6、8、10;
5、12、13; 7、24、25;
8、15、17; 9、40、41.
ak,bk,ck; 2n,n2-1,n2+1.
2n+1, 2n2+2n, 2n2+2n+1(n,k>0)
满足a2 +b2=c2的三个正整数,称为勾股数
疑点点拨
2、在△ABC中,AC=6,BC=8,则AB的长为( )
A 10 B 2 C 4 D 无法确定
3、已知直角三角形的两边长分别为3、4,则第三边长为 。
1、命题“直角三角形中30°角所对的直角边等于斜边的一半”的逆命题是 。
D
5、特殊三角形的三边关系:
若∠A=30°,则
若∠A=45°,则
考 点 一
与勾股定理有关的
计算问题
比一比,看谁快!
1、在Rt△ABC中,∠C=900
①若a=6,b=8, 则c=___;
10
9
4
③若a:b=1:2,c= 2 ,则S△ABC=____;
②若a=40,c=41,则b=____;
a
b
c
2、分别以直角三角形三边为半径作正方形则这三个正方形的面积S1, S2, S3之间的关系( )
S3 = S1 + S2
C
B
A
S
3
S
2
S
1
C
B
A
S
3
S
2
S
1
a
b
S
3
S
2
S
1
c
3、等腰三角形底边上的高为8,周长为32,求这个三角形的面积
8
x
16-x
D
A
B
C
解:设这个三角形为ABC,高为AD,设BD为x,则AB为(16-x),
由勾股定理得:
x2+82=(16-x)2
即x2+64=256-32x+x2
∴ x=6
∴ S?ABC=BC?AD/2=2 ?6 ?8/2=48
4、(教材P29)如图,已知直角三角形ABC的三边分别为6、8、10,分别以它的三边为直径向上作三个半圆,求图中阴影部分的面积.
5、已知:如图,∠B=∠D=90°,∠A=60°,AB=4,CD=2,求:四边形ABCD的面积。
考 点 3
与勾股定理有关的证明题
1、如图,已知在△ABC中,∠C=90°,D为AC上一点,AB2-BD2与AC2-DC2有怎样的关系?试证明你的结论。
证明:
在Rt △ABC中,
AB2=AC2+BC2
在Rt △DBC中,
BD2=DC2+BC2
∴ BC2 = AB2—AC2
BC2 = BD2 — DC2
∴ AB2—AC2 = BD2 — DC2
∵ ∠C=90°
即: AB2-BD2 = AC2-DC2
2、已知,△ABC中,AB=17cm,BC=16cm,BC边上的中线AD=15cm,试说明△ABC是等腰三角形。
提示: 先运用勾股定理证明中线AD⊥BC,再利用等腰三角形的判定方法就可以说明了.
考 点 4
勾股定理的实际应用
2、如图,点A是一个半径为 250 m的圆形森林公园的中心,在森林公园附近有 B 、C 两个小镇,现要在 B、C 两小镇之间修一条长为 1000 m 的笔直公路将两镇连通,经测得 ∠B=60°,∠C=30°,问:请通过计算说明此公路会不会穿过该森林公园?
A
B
C
250
1000
60°
30°
D
解:在△ABC中∠B=60°,∠C=30°,
∴∠BAC=900
∴在Rt△ABC中,AB= BC=500
AC= =500
∵2S△ABC=AD×BC=AB×AC
∴AD=250 >250
∴此公路不会穿过该森林公园
3、如图,A市气象测得台风中心在A市正东方向300千米的B处,以 千米每时的速度向北偏西60°的方向移动,距台风中心200千米范围内是会受到台风影响范围。
(1)A市是否会受台风影响?说明理由;
(2)若A市受影响,那么受台风影响的时间为多久?
B
北
60°
东
A
C
勾股定理逆定理的应用
考点5
如果三角形的三边长a,b,c满足a2 +b2=c2 ,
那么这个三角形是直角三角形
我满足
a2 +b2=c2 ,
a
b
c
我是直角三角形
跟踪训练:教材P39第9题
1、在矩形纸片ABCD中,AD=4cm,AB=10cm,按图所示方式折叠,使点B与点D重合,折痕为EF,求DE的长?
A
B
C
D
E
F
C’
六、利用方程解决翻折问题
