人教版九年级上册24.2.1 点和圆的位置关系课件(35张)
文档属性
| 名称 | 人教版九年级上册24.2.1 点和圆的位置关系课件(35张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-19 00:00:00 | ||
图片预览


文档简介
24.2.1 点和圆的位置关系
r
·
C
O
A
B
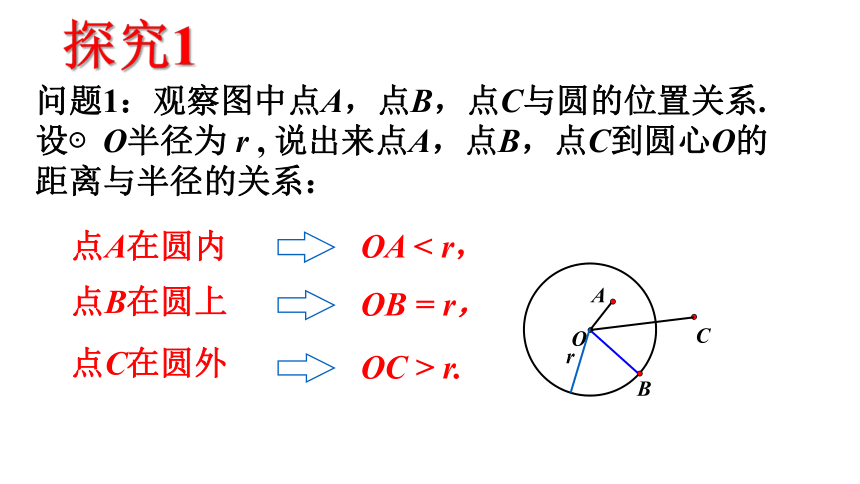
OC > r.
问题1:观察图中点A,点B,点C与圆的位置关系.设⊙O半径为 r , 说出来点A,点B,点C到圆心O的距离与半径的关系:
点C在圆外
点A在圆内
点B在圆上
OA < r,
OB = r,
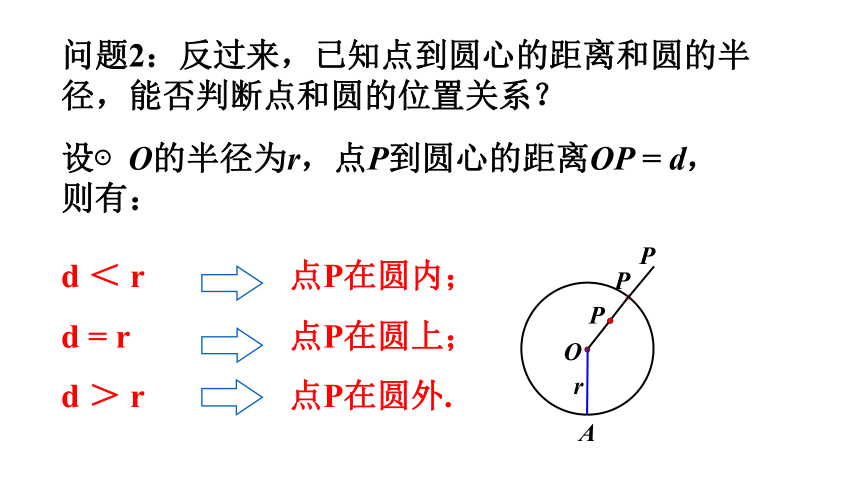
设⊙O的半径为r,点P到圆心的距离OP = d,则有:
r
·
O
A
问题2:反过来,已知点到圆心的距离和圆的半径,能否判断点和圆的位置关系?
P
P
P
d = r
d > r
d < r
点P在圆内;
点P在圆上;
点P在圆外.
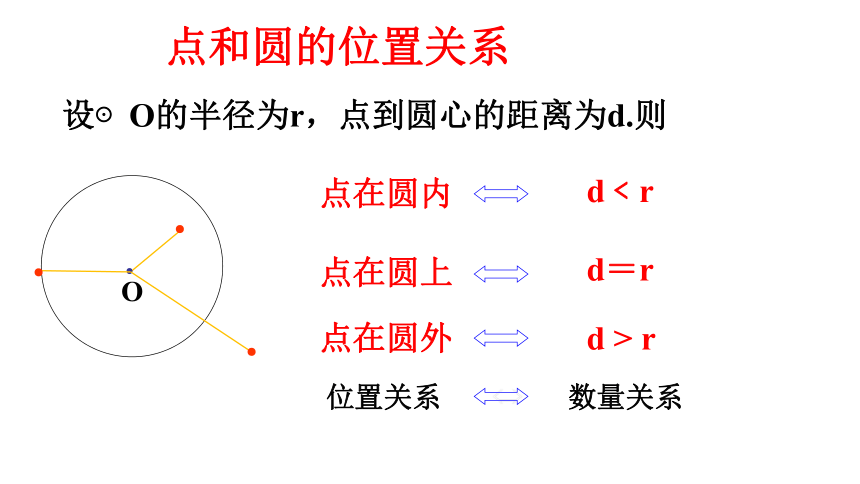
设⊙O的半径为r,点到圆心的距离为d.则
点和圆的位置关系
点在圆内
d﹤r
点在圆上
点在圆外
d=r
d > r
位置关系 数量关系
●
●
●
●
O
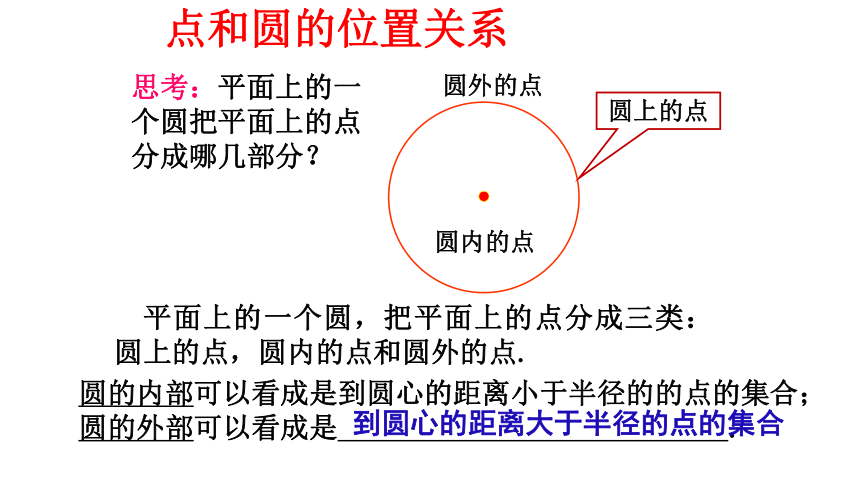
圆外的点
圆内的点
圆上的点
平面上的一个圆,把平面上的点分成三类:圆上的点,圆内的点和圆外的点.
圆的内部可以看成是到圆心的距离小于半径的的点的集合;
圆的外部可以看成是 .
到圆心的距离大于半径的点的集合
思考:平面上的一个圆把平面上的点分成哪几部分?
点和圆的位置关系
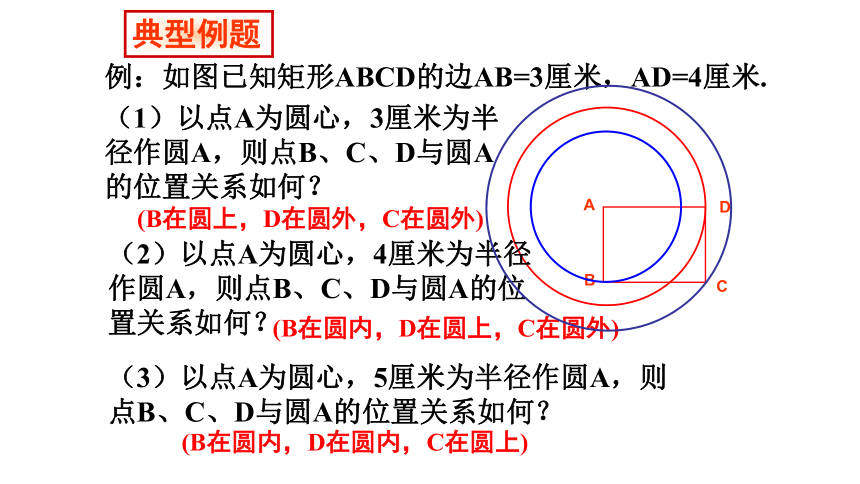
例:如图已知矩形ABCD的边AB=3厘米,AD=4厘米.
典型例题
A
D
C
B
(1)以点A为圆心,3厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
(B在圆上,D在圆外,C在圆外)
(2)以点A为圆心,4厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
(B在圆内,D在圆上,C在圆外)
(3)以点A为圆心,5厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
(B在圆内,D在圆内,C在圆上)
1.⊙O的半径6cm,A、B、C三点到圆心的距离分别为5cm、6cm、8cm,点A、B、C与⊙O的位置关系是:点A在 ;点B在 ;点C在 .
圆内
圆上
圆外
2.已知⊙O的半径为6,点P不在圆内,则线段OP 的长度的取值范围是_________.
OP≥6
3.画出由所有到已知点O的距离大于或等于2 cm,并且小于或等于3 cm的点组成的图形.
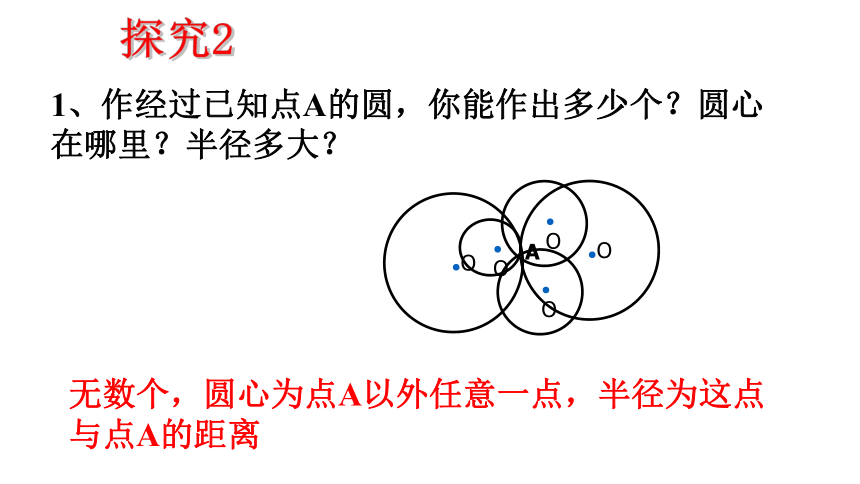
1、作经过已知点A的圆,你能作出多少个?圆心在哪里?半径多大?
●O
●A
●O
●O
●O
●O
无数个,圆心为点A以外任意一点,半径为这点与点A的距离
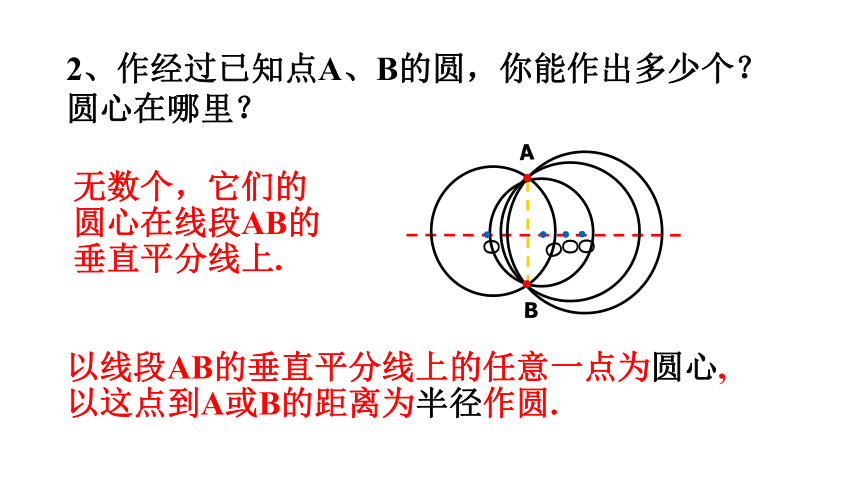
2、作经过已知点A、B的圆,你能作出多少个?圆心在哪里?
●O
● O
●O
●O
A
B
无数个,它们的圆心在线段AB的垂直平分线上.
以线段AB的垂直平分线上的任意一点为圆心,以这点到A或B的距离为半径作圆.
有且只有
位置关系
定理:
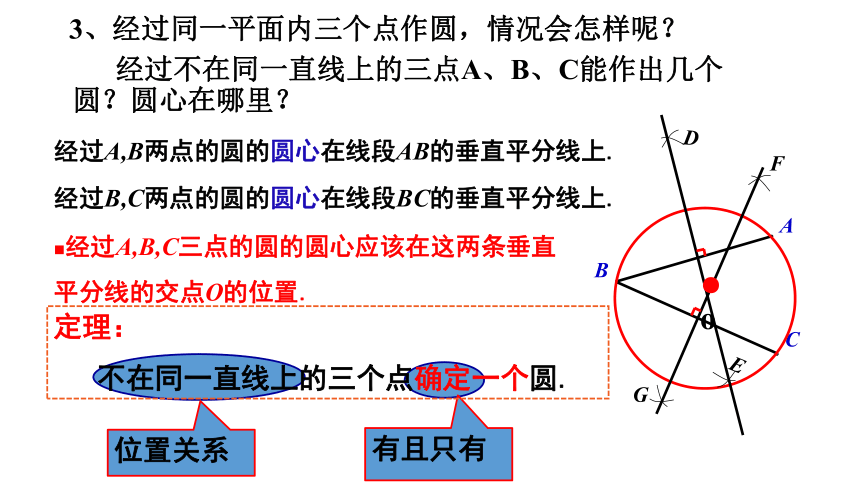
不在同一直线上的三个点确定一个圆.
A
B
C
D
E
G
F
●o
经过B,C两点的圆的圆心在线段BC的垂直平分线上.
经过A,B,C三点的圆的圆心应该在这两条垂直平分线的交点O的位置.
经过A,B两点的圆的圆心在线段AB的垂直平分线上.
经过不在同一直线上的三点A、B、C能作出几个圆?圆心在哪里?
3、经过同一平面内三个点作圆,情况会怎样呢?
A
B
C
●O
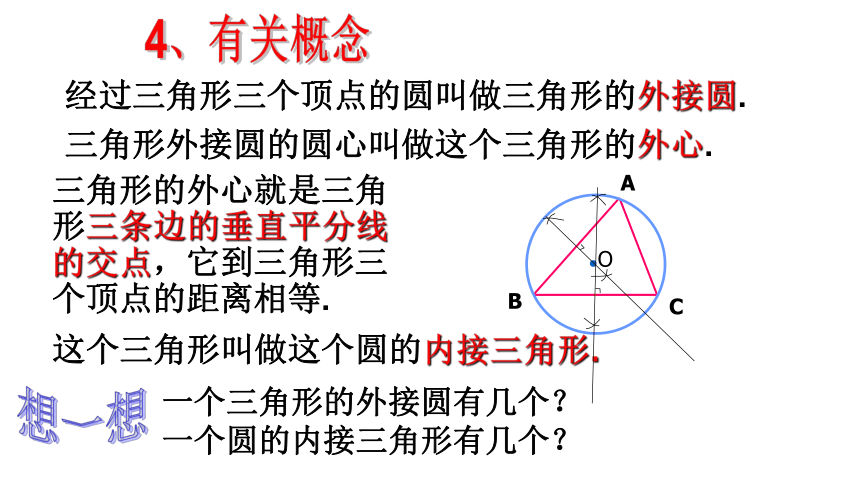
经过三角形三个顶点的圆叫做三角形的外接圆.
这个三角形叫做这个圆的内接三角形.
三角形的外心就是三角形三条边的垂直平分线的交点,它到三角形三个顶点的距离相等.
三角形外接圆的圆心叫做这个三角形的外心.
一个三角形的外接圆有几个?
一个圆的内接三角形有几个?
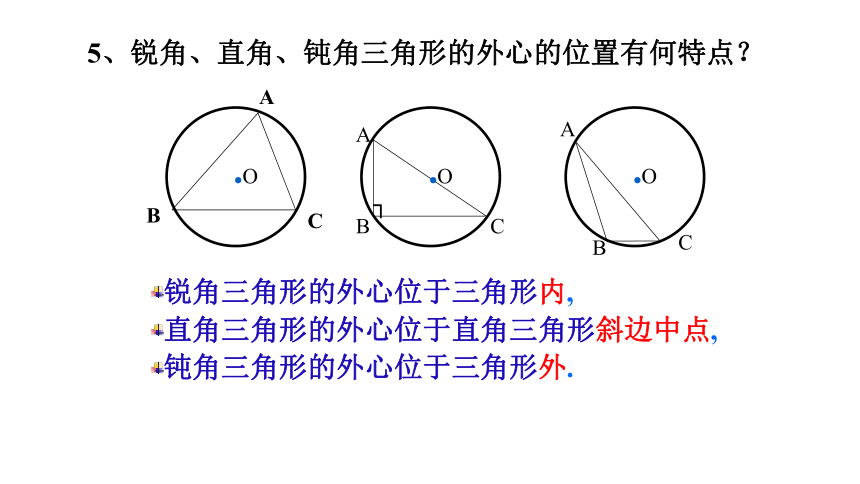
锐角三角形的外心位于三角形内,
直角三角形的外心位于直角三角形斜边中点,
钝角三角形的外心位于三角形外.
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
5、锐角、直角、钝角三角形的外心的位置有何特点?
1、判断
(1)任意的一个三角形一定有一个外接圆.
(2)任意一个圆有且只有一个内接三角形.
(3)经过三点一定可以作圆.
(4)三角形的外心就是这个三角形两边垂直平 分线的交点.
(5)三角形的外心到三边的距离相等.
(6)三角形的外心到三角形各顶点的距离相等.
A
B
C
O
2、一位考古学家发现一块圆形破镜碎片,你能帮助他找出这个破镜的半径吗?
1、已知⊙O的半径为4,OP=3.4,则P在⊙O的________
2、已知 点P在 ⊙O的外部,OP=5,那么⊙O的半径r满足____________
3、 已知⊙O的半径为5,M为ON的中点,当OM=3时,N点与⊙O的位置关系是N在⊙O的__________
内部
0﹤r ﹤5
外部
4、在△ABC中,∠C=90°,AB=5cm,BC=4 cm,以点A为圆心,以3 cm为半径作圆,请判断:
(1)C点与⊙A的位置关系;
(2)B点与⊙A的位置关系;
(3)AB的中点D与⊙A的位置关系.
B
C
A
D
(1)点C在⊙A 上
(2)点B在⊙A 外
(3)点D在⊙A 内
5cm
4cm
3cm
解:
5、如图,等腰ΔABC中, ,
,点O为外心,求外接圆的半径.
O
A
D
C
B
这节课你学习到了哪些内容?
反证法
路边苦李
王戎7岁时,与小伙伴们外出游玩,看到路边的李树上结满了果子.小伙伴们纷纷去摘取果子,只有王戎站在原地不动.有人问王戎为什么?
王戎回答说:“树在道边而多子,此必苦李.”
小伙伴摘取一个尝了一下果然是苦李.
王戎是怎样知道李子是苦的呢?他运用了怎样的推理方法?
假设李子是甜的
那么李子会被过路人摘去解渴,树上的李子会很少。
事实上树上的李子很多,这与事实相矛盾。
造成矛盾的原因是:假设李子是甜的,这个假设是错误的,说明原来的结论:路边的李子是苦的是正确的。
反证法
在△ABC中,若AB≠AC,
则∠B≠∠C.如何说明呢?
方 法 迁 移
C
B
A
假设李子是甜的
假设∠B=∠C
那么AB=AC,
这与已知条件AB≠AC相矛盾
假设不正确,则∠B≠∠C
假设不正确,则李子是苦的。
那么李子会被过路人摘去解渴,则李子会很少,这与事实相矛盾。
方法迁移
问题:
探究:
这种证明方法与前面的证明方法不同,它是先假设命题结论反面成立,从假设出发,经过推理得出和已知条件(定义、公理、定理等)矛盾,从而得出假设命题不成立,即所求证的命题正确。像这种证明方法叫做反证法。
发 现 新 知
反证法的一般步骤
探究新知
思考:过同一直线上的三点可以作圆吗?
过同一直线上的三点不能作圆.
反证法的步骤:
(1)假设原命题不成立;
(2)以此为依据进行推理,得出矛盾(与公理、定理或条件矛盾);
(3)得出假设不成立,从而原命题成立;
如图,已知点A、B、C在直线m上.
求证:过点A、B、C不能作圆.
l1
l2
A
B
C
P
过同一直线上的三点不能作圆
反证法
l
例 用反证法证明(填空):在一个三角形中,至少有一个内角大于或等于60°.
已知:如图, △ABC.
求证: ∠A,∠B,∠C中至少有一个内角大于或等于60° .
证明:
A
B
C
应 用 新 知
题设
结论
假设△ABC中没有一个内角大于或等于60°,
即 ∠A__ 60° , ∠B__ 60° ,∠C__ 60°
<
<
<
则 ∠A+∠B+∠C__ 180°
<
这与 “三角形的内角和等于180°”矛盾
所以假设命题不成立,
即所求证的结论成立.
求证:平行于同一直线的两直线平行.
如图,已知点a∥c,b∥c
求证:a∥b
1、已知:如图,直线a,b被直线c所截,∠1 ≠ ∠2
求证:a∥b
∴∠1=∠2 (两直线平行,同位角相等)
这与已知的∠1≠∠2矛盾
∴假设不成立
证明:假设结论不成立,则a∥b
∴a∥b
试一试
2、如图,在△ABC中,AB=c,BC=a, AC=b,∠C≠90°”,请问结论a2 +b2 ≠ c2 成立吗?请说明理由.
A
C
B
a
b
c
证明:假设a2 +b2 =c2,由勾股定理逆定理可知三角形ABC是直角三角形,且∠C=90°,这与已知条件∠C≠90°矛盾。假设不成立,从而说明原结论a2 +b2 ≠ c2 成立。
课 堂 小 结
1、反证法的定义;
2、反证法的证明步骤;
3、理解并掌握反证法的证明技巧。
这节课你有什么收获?
(1)课本P82练习
第 1 题
(2)课本P82习题29.2
第 2、3 题
思考题:什么时候运用反证法?
作 业
警察局里有5名嫌疑犯,他们分别做了如下口供:
A说:这里有1个人说谎.
B说:这里有2个人说谎.
C说:这里有3个人说谎.
D说:这里有4个人说谎.
E说:这里有5个人说谎.
聪明的同学们,假如你是警察,你觉得谁说了真话?
你会释放谁?
请与大家分享你的判断!
r
·
C
O
A
B
OC > r.
问题1:观察图中点A,点B,点C与圆的位置关系.设⊙O半径为 r , 说出来点A,点B,点C到圆心O的距离与半径的关系:
点C在圆外
点A在圆内
点B在圆上
OA < r,
OB = r,
设⊙O的半径为r,点P到圆心的距离OP = d,则有:
r
·
O
A
问题2:反过来,已知点到圆心的距离和圆的半径,能否判断点和圆的位置关系?
P
P
P
d = r
d > r
d < r
点P在圆内;
点P在圆上;
点P在圆外.
设⊙O的半径为r,点到圆心的距离为d.则
点和圆的位置关系
点在圆内
d﹤r
点在圆上
点在圆外
d=r
d > r
位置关系 数量关系
●
●
●
●
O
圆外的点
圆内的点
圆上的点
平面上的一个圆,把平面上的点分成三类:圆上的点,圆内的点和圆外的点.
圆的内部可以看成是到圆心的距离小于半径的的点的集合;
圆的外部可以看成是 .
到圆心的距离大于半径的点的集合
思考:平面上的一个圆把平面上的点分成哪几部分?
点和圆的位置关系
例:如图已知矩形ABCD的边AB=3厘米,AD=4厘米.
典型例题
A
D
C
B
(1)以点A为圆心,3厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
(B在圆上,D在圆外,C在圆外)
(2)以点A为圆心,4厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
(B在圆内,D在圆上,C在圆外)
(3)以点A为圆心,5厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
(B在圆内,D在圆内,C在圆上)
1.⊙O的半径6cm,A、B、C三点到圆心的距离分别为5cm、6cm、8cm,点A、B、C与⊙O的位置关系是:点A在 ;点B在 ;点C在 .
圆内
圆上
圆外
2.已知⊙O的半径为6,点P不在圆内,则线段OP 的长度的取值范围是_________.
OP≥6
3.画出由所有到已知点O的距离大于或等于2 cm,并且小于或等于3 cm的点组成的图形.
1、作经过已知点A的圆,你能作出多少个?圆心在哪里?半径多大?
●O
●A
●O
●O
●O
●O
无数个,圆心为点A以外任意一点,半径为这点与点A的距离
2、作经过已知点A、B的圆,你能作出多少个?圆心在哪里?
●O
● O
●O
●O
A
B
无数个,它们的圆心在线段AB的垂直平分线上.
以线段AB的垂直平分线上的任意一点为圆心,以这点到A或B的距离为半径作圆.
有且只有
位置关系
定理:
不在同一直线上的三个点确定一个圆.
A
B
C
D
E
G
F
●o
经过B,C两点的圆的圆心在线段BC的垂直平分线上.
经过A,B,C三点的圆的圆心应该在这两条垂直平分线的交点O的位置.
经过A,B两点的圆的圆心在线段AB的垂直平分线上.
经过不在同一直线上的三点A、B、C能作出几个圆?圆心在哪里?
3、经过同一平面内三个点作圆,情况会怎样呢?
A
B
C
●O
经过三角形三个顶点的圆叫做三角形的外接圆.
这个三角形叫做这个圆的内接三角形.
三角形的外心就是三角形三条边的垂直平分线的交点,它到三角形三个顶点的距离相等.
三角形外接圆的圆心叫做这个三角形的外心.
一个三角形的外接圆有几个?
一个圆的内接三角形有几个?
锐角三角形的外心位于三角形内,
直角三角形的外心位于直角三角形斜边中点,
钝角三角形的外心位于三角形外.
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
5、锐角、直角、钝角三角形的外心的位置有何特点?
1、判断
(1)任意的一个三角形一定有一个外接圆.
(2)任意一个圆有且只有一个内接三角形.
(3)经过三点一定可以作圆.
(4)三角形的外心就是这个三角形两边垂直平 分线的交点.
(5)三角形的外心到三边的距离相等.
(6)三角形的外心到三角形各顶点的距离相等.
A
B
C
O
2、一位考古学家发现一块圆形破镜碎片,你能帮助他找出这个破镜的半径吗?
1、已知⊙O的半径为4,OP=3.4,则P在⊙O的________
2、已知 点P在 ⊙O的外部,OP=5,那么⊙O的半径r满足____________
3、 已知⊙O的半径为5,M为ON的中点,当OM=3时,N点与⊙O的位置关系是N在⊙O的__________
内部
0﹤r ﹤5
外部
4、在△ABC中,∠C=90°,AB=5cm,BC=4 cm,以点A为圆心,以3 cm为半径作圆,请判断:
(1)C点与⊙A的位置关系;
(2)B点与⊙A的位置关系;
(3)AB的中点D与⊙A的位置关系.
B
C
A
D
(1)点C在⊙A 上
(2)点B在⊙A 外
(3)点D在⊙A 内
5cm
4cm
3cm
解:
5、如图,等腰ΔABC中, ,
,点O为外心,求外接圆的半径.
O
A
D
C
B
这节课你学习到了哪些内容?
反证法
路边苦李
王戎7岁时,与小伙伴们外出游玩,看到路边的李树上结满了果子.小伙伴们纷纷去摘取果子,只有王戎站在原地不动.有人问王戎为什么?
王戎回答说:“树在道边而多子,此必苦李.”
小伙伴摘取一个尝了一下果然是苦李.
王戎是怎样知道李子是苦的呢?他运用了怎样的推理方法?
假设李子是甜的
那么李子会被过路人摘去解渴,树上的李子会很少。
事实上树上的李子很多,这与事实相矛盾。
造成矛盾的原因是:假设李子是甜的,这个假设是错误的,说明原来的结论:路边的李子是苦的是正确的。
反证法
在△ABC中,若AB≠AC,
则∠B≠∠C.如何说明呢?
方 法 迁 移
C
B
A
假设李子是甜的
假设∠B=∠C
那么AB=AC,
这与已知条件AB≠AC相矛盾
假设不正确,则∠B≠∠C
假设不正确,则李子是苦的。
那么李子会被过路人摘去解渴,则李子会很少,这与事实相矛盾。
方法迁移
问题:
探究:
这种证明方法与前面的证明方法不同,它是先假设命题结论反面成立,从假设出发,经过推理得出和已知条件(定义、公理、定理等)矛盾,从而得出假设命题不成立,即所求证的命题正确。像这种证明方法叫做反证法。
发 现 新 知
反证法的一般步骤
探究新知
思考:过同一直线上的三点可以作圆吗?
过同一直线上的三点不能作圆.
反证法的步骤:
(1)假设原命题不成立;
(2)以此为依据进行推理,得出矛盾(与公理、定理或条件矛盾);
(3)得出假设不成立,从而原命题成立;
如图,已知点A、B、C在直线m上.
求证:过点A、B、C不能作圆.
l1
l2
A
B
C
P
过同一直线上的三点不能作圆
反证法
l
例 用反证法证明(填空):在一个三角形中,至少有一个内角大于或等于60°.
已知:如图, △ABC.
求证: ∠A,∠B,∠C中至少有一个内角大于或等于60° .
证明:
A
B
C
应 用 新 知
题设
结论
假设△ABC中没有一个内角大于或等于60°,
即 ∠A__ 60° , ∠B__ 60° ,∠C__ 60°
<
<
<
则 ∠A+∠B+∠C__ 180°
<
这与 “三角形的内角和等于180°”矛盾
所以假设命题不成立,
即所求证的结论成立.
求证:平行于同一直线的两直线平行.
如图,已知点a∥c,b∥c
求证:a∥b
1、已知:如图,直线a,b被直线c所截,∠1 ≠ ∠2
求证:a∥b
∴∠1=∠2 (两直线平行,同位角相等)
这与已知的∠1≠∠2矛盾
∴假设不成立
证明:假设结论不成立,则a∥b
∴a∥b
试一试
2、如图,在△ABC中,AB=c,BC=a, AC=b,∠C≠90°”,请问结论a2 +b2 ≠ c2 成立吗?请说明理由.
A
C
B
a
b
c
证明:假设a2 +b2 =c2,由勾股定理逆定理可知三角形ABC是直角三角形,且∠C=90°,这与已知条件∠C≠90°矛盾。假设不成立,从而说明原结论a2 +b2 ≠ c2 成立。
课 堂 小 结
1、反证法的定义;
2、反证法的证明步骤;
3、理解并掌握反证法的证明技巧。
这节课你有什么收获?
(1)课本P82练习
第 1 题
(2)课本P82习题29.2
第 2、3 题
思考题:什么时候运用反证法?
作 业
警察局里有5名嫌疑犯,他们分别做了如下口供:
A说:这里有1个人说谎.
B说:这里有2个人说谎.
C说:这里有3个人说谎.
D说:这里有4个人说谎.
E说:这里有5个人说谎.
聪明的同学们,假如你是警察,你觉得谁说了真话?
你会释放谁?
请与大家分享你的判断!
同课章节目录
